基于重合度优化的电驱动系统齿轮振动噪声性能改善
2024-01-10吴佐来鲁方俊
程 翔, 吴佐来, 鲁方俊
(无锡中车浩夫尔动力总成有限公司,无锡 214174)
随着生活水平的提高,人们对汽车的性能品质要求越来越高,NVH(振动噪声与声振粗糙度)作为乘客最直观感受的一项性能,越来越受到大家的关注和重视.电动汽车因采用电机替换传统的发动机,没有发动机噪声的掩蔽,且电机转速相较于发动机更高,减速器齿轮噪声也越突出,对于设计和加工制造的要求也越高,在电驱动产品开发的全周期内,均要重点关注NVH性能的表现.
齿轮噪声产生的原因有很多,从整个电驱动系统来说,可以分为源、路径和响应.源一般指噪声产生的来源,即齿轮啮合激励;路径指激励传递的介质如电驱系统壳体,整车悬置,底盘和空气;响应一般指车内如驾驶舱车身及空腔.其中源和路径是设计主要关注的方向.针对某项目电驱动产品齿轮噪声大的问题,通过仿真方法,指导设计优化齿轮激励源大小,并结合NVH测试结果,来验证方案的效果.
1 齿轮啮合激励
齿轮啮合过程中,由于同时参与啮合的齿轮对数的变化,齿轮受载时发生弯曲、弹性及扭转变形,齿轮的加工和安装误差等,导致齿轮动态啮合力的产生,继而引发了齿轮系统的振动和噪声.其中,齿轮啮合对数的变化及齿轮受载变形产生的时变啮合刚度激励,此部分因素主要与齿轮设计参数有关,故也称为“设计传递误差激励”[1].文中主要研究此激励,即主要从设计角度来分析和优化齿轮,以提高齿轮NVH性能水平.
同时参与啮合的齿轮对数即重合度,是齿轮设计和优化时需要重点考虑的参数.重合度分端面重合度εα和轴向重合度εβ,总重合度εγ为两者之和.对于新能源电驱系统常用的斜齿轮,端面重合度εα计算公式为[2]
(1)
式中:z1,z2分别为啮合齿轮对的齿数;αa1,αa1分别为两齿轮端面齿顶圆压力角;αt为端面压力角.
轴向重合度εβ计算公式为
(2)
式中:b为齿轮齿宽;β为螺旋角;mn为法向模数.
2 齿轮啮合接触线长度
斜齿轮在啮合过程中,是从从动轮的前端面齿顶一点开始接触,随着啮合进行,接触线由短变长,再由长变短,最后在从动轮后端面齿根一点脱离.随着啮合线长度的变化,即产生动态的接触载荷激励.总的啮合接触线是同时参与啮合齿轮对的啮合接触线的总和,故齿轮重合度直接影响啮合接触线的长度,是齿轮设计和优化过程中的重要指标参数.
齿轮啮合接触线长度不是固定值,而是随时间变化的动态值,一般采用统计规律计算,参考文献[3-4]中接触线具体公式为
(3)


(4)
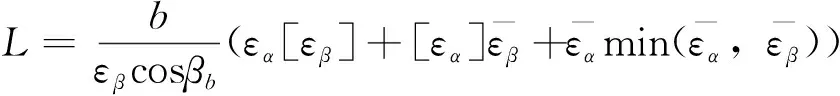
(5)
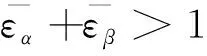
(6)
(7)
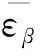
上述公式提供了很好的量化参考,便于后续进行重合度设计选型及优化.
3 齿轮NVH优化改善
3.1 齿轮宏观参数优化
齿轮的宏观参数是NVH性能设计的基础,良好的宏观参数设计和与之匹配的微观参数设计,才能最终保证齿轮具备较优秀的NVH性能水平[5-6].当齿轮宏观参数设计不合理或者关键设计指标过低时,齿轮微观修形将变的非常困难或者失去意义,NVH将很难达到理想表现.
文献[7]研究了轴向重合度对齿轮接触线长度和传递误差的影响,文献[8]用仿真方法验证了实际重合度对啮合刚度和传递误差的影响,文献[9]研究了齿轮渐开线形状、起始点及重合度对啮合刚度和传递误差的影响.合理并且较优的宏观参数是齿轮具备优异NVH表现的基本保证,其中,重合度设计是其中的重点.合理的重合度设计能降低齿轮啮合动态激励力,减小齿轮啮合传递误差,改善齿轮接触斑点,并能大大降低后续微观修形的难度,降低修形参数敏感性,增加加工制造和量产NVH性能的鲁棒性.
上述文献均在仿真维度进行研究,没有实际的工程结果验证.文中基于上述理论及经验,结合实际案例,进行了重合度优化方案的闭环验证.
某新能源汽车电驱动120 kW项目三合一产品在开发过程中,发现整车加速过程全程车内啸叫偏大,主观评价较差.采集驾驶员右耳噪声数据,分析发现啸叫主要表现为减速器第一级齿轮22阶噪声.如图1所示,在频谱彩图中,22阶阶次线在全转速范围内均高亮突出,且无明显的共振问题,阶次值也超过客户指标要求.故判断啸叫问题原因为22阶齿轮啮合激励振动过大,需要对齿轮啮合进行优化改善.后尝试对该对齿轮进行修形优化,效果均表现不好.在重新评估齿轮设计参数时,发现关键设计参数不合理,齿轮啮合重合度太小,决定进行设计变更,重新进行齿轮宏观选型设计,增大重合度.

图1 全电门加速工况车内噪声谱图
在兼顾原壳体空间结构不变,保证齿轮强度、润滑及耐久性能合格的基础上进行齿轮参数优化,具体参数见表1.宏观参数优化后,齿轮端面重合度由1.71提高到1.92,轴向重合度由原来的2.1提高到3.05,总重合度由3.81提高到4.97.
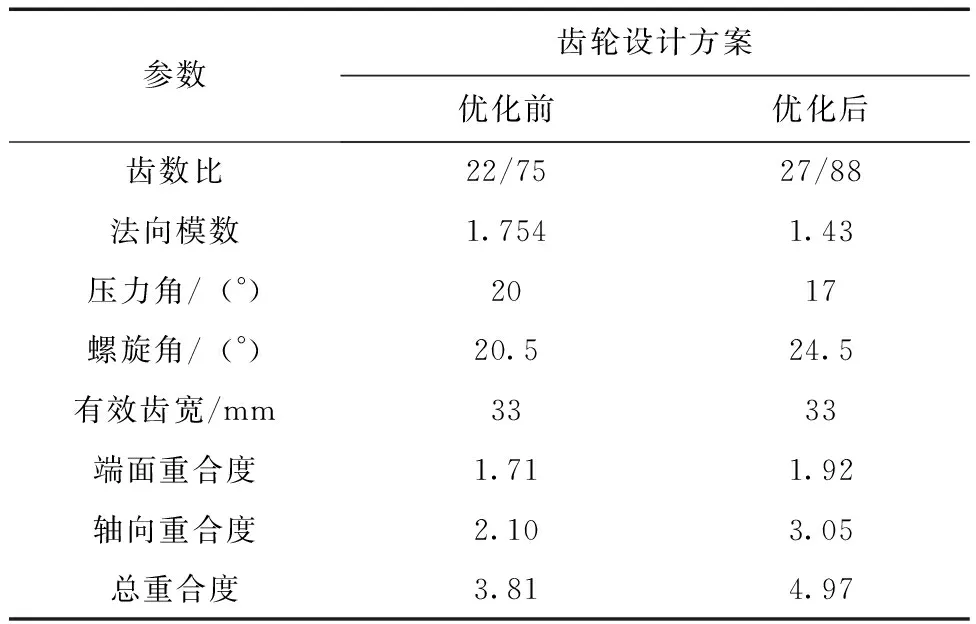
表1 齿轮参数优化前后数值
依据公式(4)~(7)所示,齿轮啮合接触线长度同时受端面重合度和轴向重合度的影响.将表1中的齿轮优化前后的端面重合度1.71和1.92分别代入公式(4)~(7)中,对轴向重合度在2~3.5范围内进行0.1间隔的分别离散取值,计算出啮合接触线长度L(最大值和最小值),并绘制出接触线长度随轴向重合度εβ变化规律,如图2所示.图中,光滑虚线和实线分别表示端面重合度为原方案1.71和新方案1.92时接触线最小长度随轴向重合度变化曲线,带三角形虚线和实线分别表示端面重合度为原方案1.71和新方案1.92时接触线最大长度随轴向重合度变化曲线.从图中可以看出,新方案端面重合度提高为1.92后,齿轮啮合接触线最小长度和最大长度均较原方案更长,且最大长度和最小长度之间的差值变小,波动值减小,且当轴向重合度取整时,接触线最大值和最小值相等,接触线长度保持不变,此时齿轮啮合激励波动相对最小.新方案轴向重合由2.1提高到3.05后,啮合接触线长度即由59.62 mm增加到69.11 mm,长度明显增大,优于原方案.
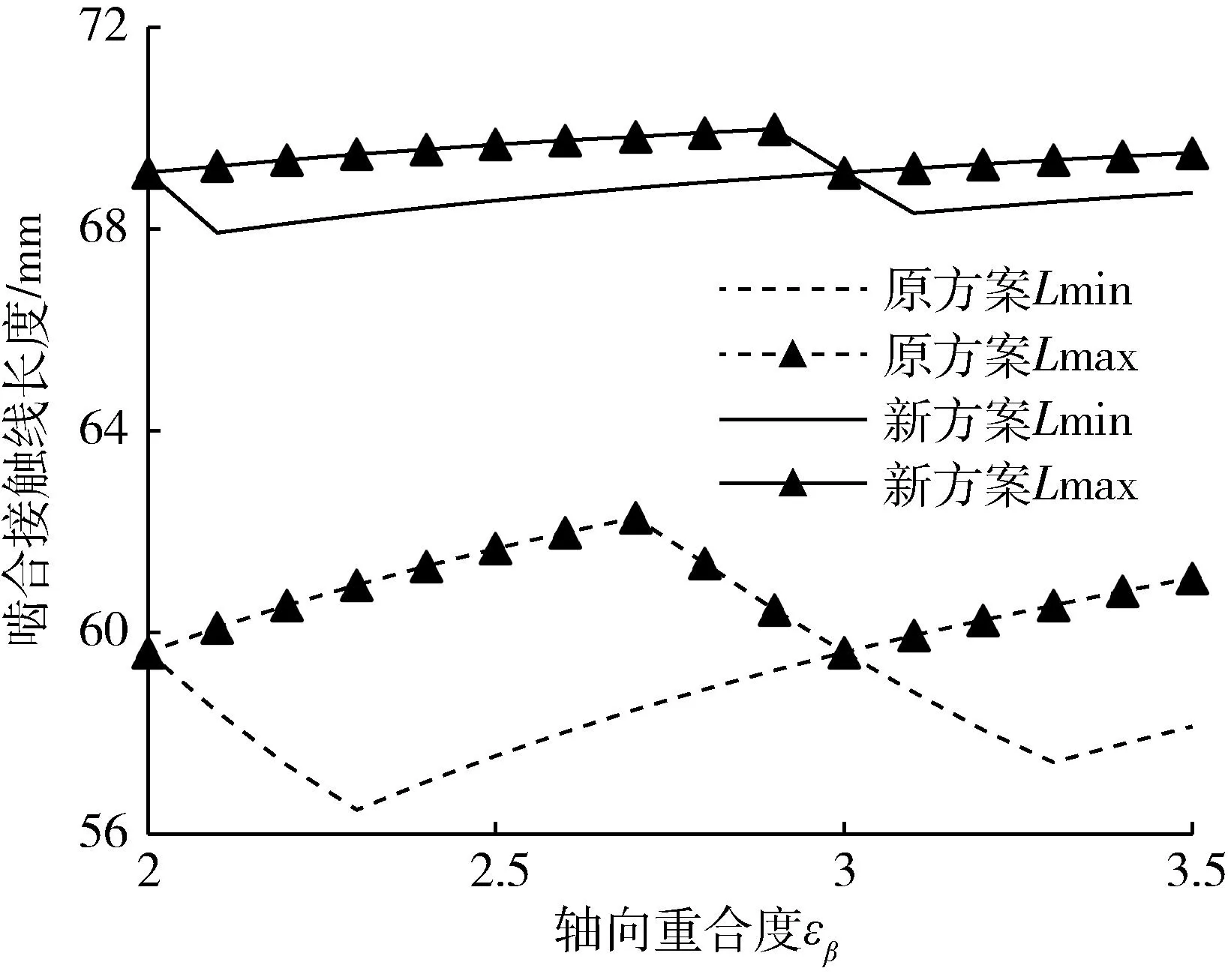
图2 齿轮啮合接触线长度L随轴向量重合度εβ的变化
3.2 齿轮微观参数优化
文中基于Masta齿轮动力学专用仿真分析软件,搭建了齿轮接触斑点仿真分析模型,如图3所示.为验证仿真分析模型的准确性,对新的宏观参数齿轮进行了接触斑点测试,如图4所示为台架测试装配图.

图3 齿轮接触斑点仿真模型

图4 齿轮接触斑点测试装配图
测试结果和仿真结果比较见图5和图6.分别比较了大扭矩工况200 Nm和小扭矩工况80 Nm的齿轮接触情况.从结果可以看出,大扭矩工况和小扭矩工况,第一级大小齿轮仿真和测试的接触斑点均居中表现,两者基本匹配,说明仿真结果准确,可以在此模型基础上进行后续的齿轮修形工作.
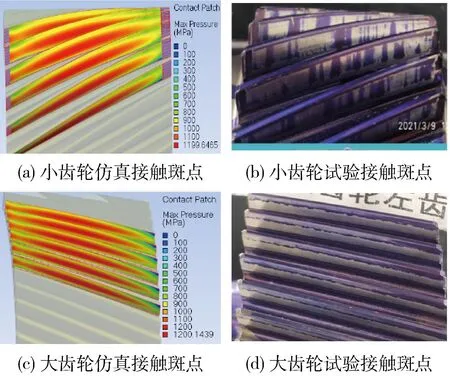
图5 接触斑点仿真与测试对比(200 Nm)

图6 接触斑点仿真与测试对比(80 Nm)
齿轮啮合重合度提高后,齿轮啮合过程受载会更平稳,啮合错位会发生改变,即需要进行新的修形参数设计,来优化齿面接触和NVH水平.考虑到文中端面重合度大于2.5,此时基于ISO6336标准的计算方法将不再适用,故文中均采用高级LTCA计算方法,即单独考虑齿面有限元,并划分六面体网格,进行更准确的齿轮啮合刚度计算.基于此方法进行新方案的齿轮修形优化,优化结果见图7.
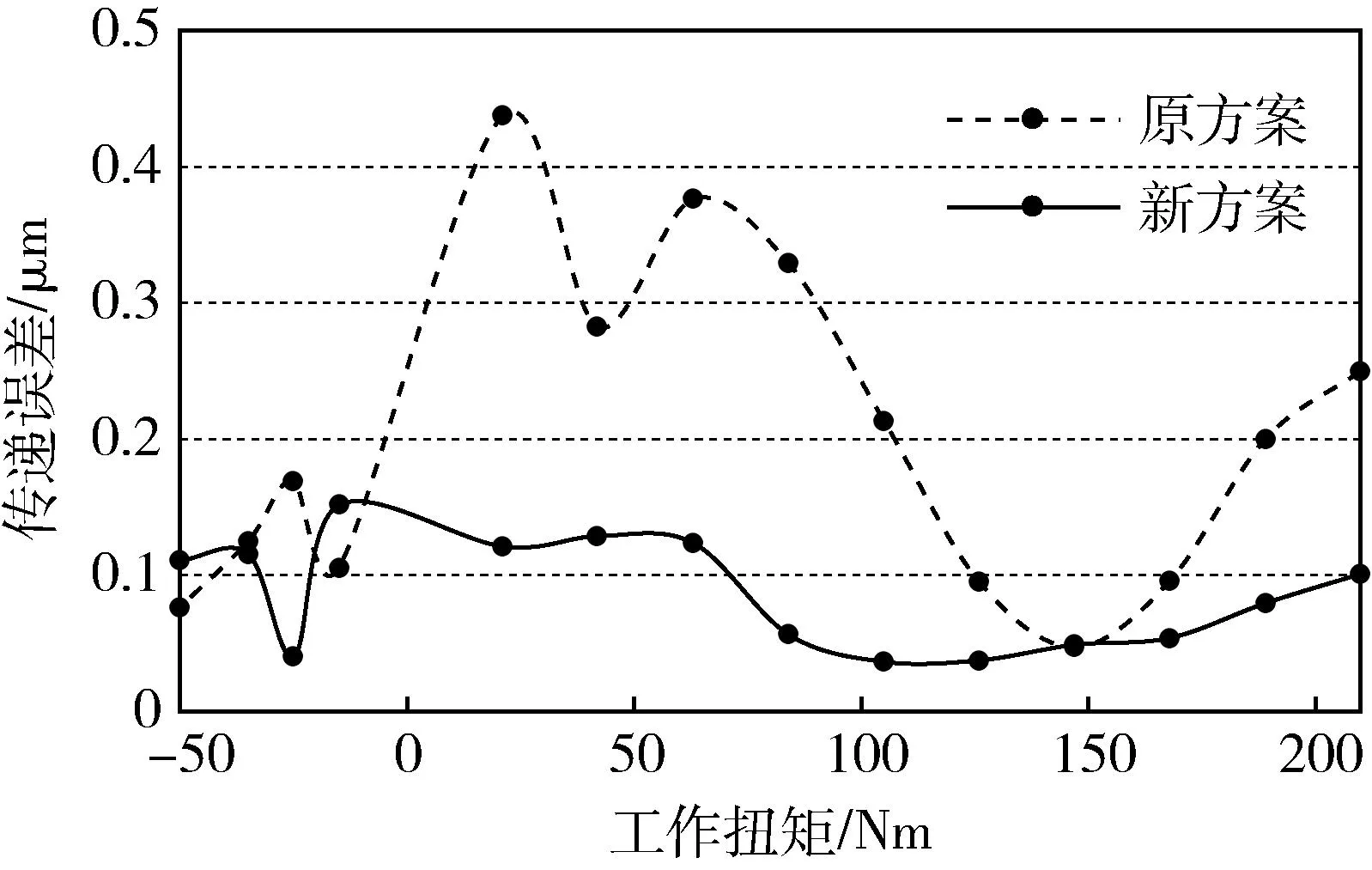
图7 齿轮传递误差优化结果
图中虚线和实线分别表示在各个扭矩工况下,原方案和新方案齿轮啮合传递误差峰峰值差值.原方案噪声问题主要集中在全电门加速工况,故主要针对大扭矩200 Nm工况进行修形优化,同时兼顾小扭矩传递误差.经过增加齿轮重合度,并进行新的修形优化后,最大扭矩时,新方案传递误差减小0.15 μm,且在其他扭矩工况如0-150 Nm区间传递误差均大幅度减小,新方案整体传递误差曲线较原方案改善较大,符合设计预期.
3.3 测试试验验证
依照新的修形方案加工齿轮样件,并进行齿面三截面检测,确保加工参数符合修形设计方案及其它关键尺寸公差要求.装配样机并上整车进行实车验证,测试结果如下:齿轮优化改善后,见图8,车内驾驶员右耳位置噪声谱图中,第一级齿轮27阶阶次线已不高亮凸显,优化明显.另见图9所示,相较于原方案22阶噪声,新方案27阶噪声在2 000 r/min以上转速区域整体明显减小,最大值降低20 dB(A).车内噪声主观评价由原来5.5分提升到7分,优化效果明显,主客观NVH表现均到达客户要求.
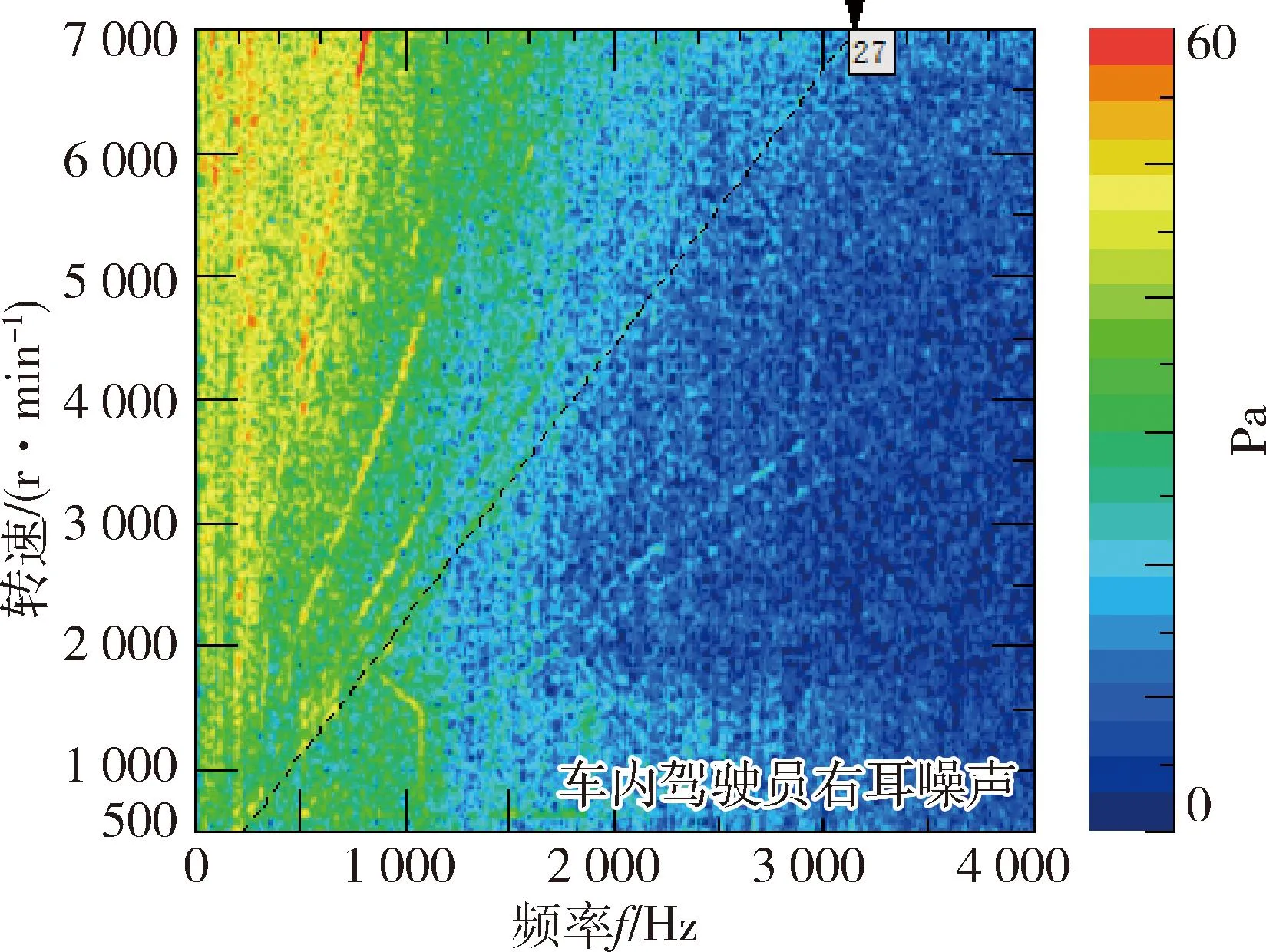
图8 优化后的样机车内噪声谱图
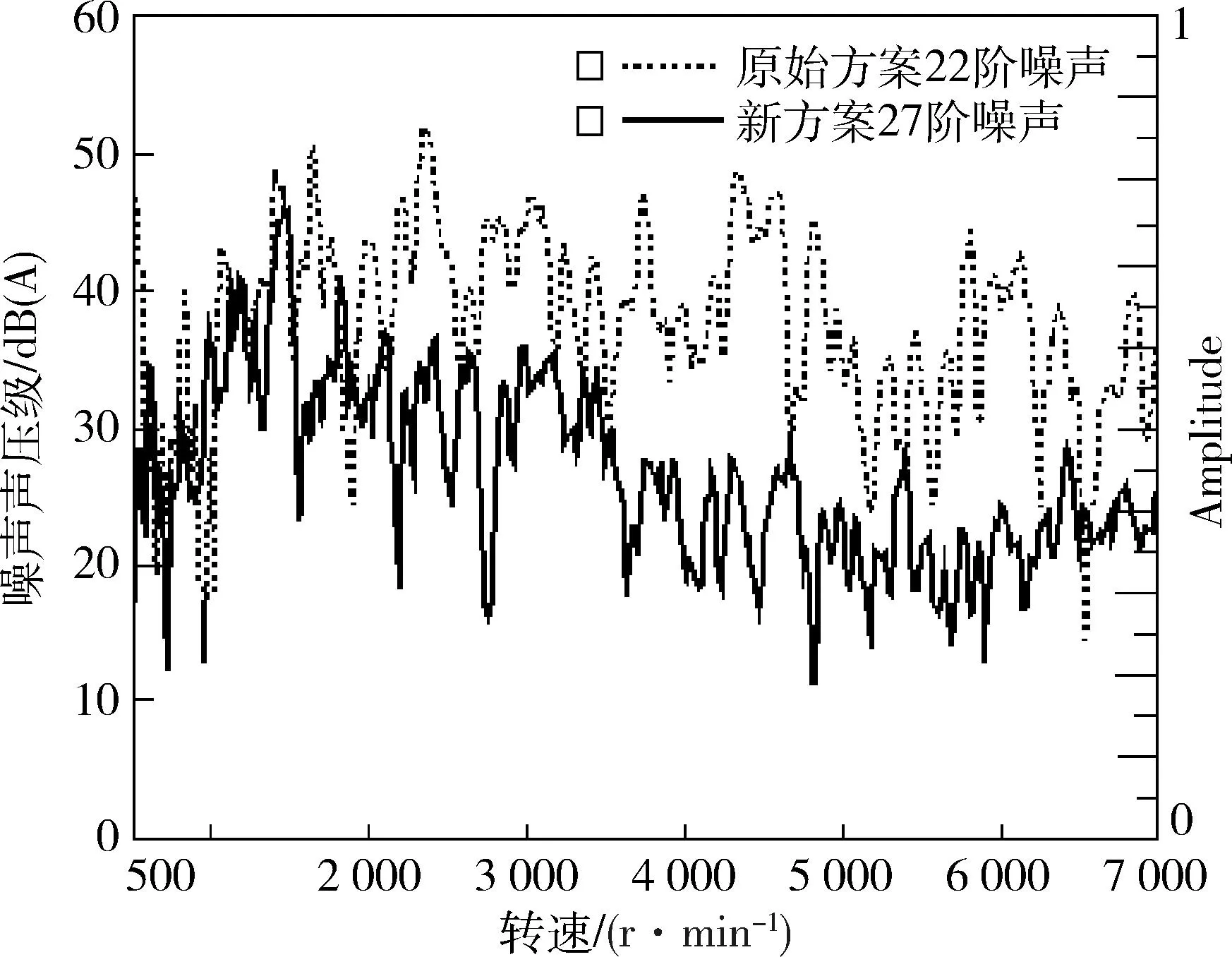
图9 齿轮优化前后阶次噪声曲线
4 结 论
重合度是齿轮NVH性能设计的重要考虑参数.文中详细分析了重合度对齿轮啮合接触线的影响,并列出了不同轴向重合度设计时,齿轮啮合接触线的变化规律,为重合度优化设计提供了具体的量化指标.针对某项目三合一产品齿轮NVH表现不良的问题,根据上述理论,并结合产品实际设计状态和调整空间,重合度由3.81提高到4.97.最终整车NVH测试结果表明,车内噪声在2 000 r/min以上转速区域整体明显减小,最大值降低20 dB(A).车内噪声主观评价由原来5.5分提升到7分,优化效果明显.为齿轮啸叫噪声问题改善及新产品设计提供了重要的经验参考.
