大跨度石油管道悬索桥风缆动力性能及优化研究
2024-01-10张嘉钦鲁佳琪刘均华游佐巧熊邵辉
张嘉钦, 鲁佳琪, 刘均华, 游佐巧, 熊邵辉
(1.国家管网集团西南油气管道有限责任公司德宏输油气分公司, 云南 德宏 678400;2.重庆正诚标研工程检测有限公司, 重庆 400713; 3.招商局重庆交通科研设计院有限公司, 重庆 400067)
美国的塔科马悬索桥建成通车不到半年就发生了坍塌事故,自该事故起,许多研究人员就开始关注风对悬索桥的作用。悬索桥的风致振动机理研究已成为当今桥梁界迫切需要解决的难题[1]。已有研究揭示,动力荷载(如车辆运行)可导致桥梁发生严重振动[2]。自20世纪末以来,中国的管道悬索桥发展迅速,有研究发现,在外部荷载(如风荷载、地震波、人员检修等)的作用下,管道悬索桥结构会发生振动。当结构体系对特定荷载的敏感性与其自身固有属性(自振频率)接近时,结构对该荷载的反应更加显著[3]。既有研究表明,桥梁结构的动态响应大小不仅受外部荷载和地震激励等因素影响,还与其自身结构的固有属性(自振频率)密切相关。
振型、周期、阻尼比、频率等是悬索桥结构的关键动力特性参数[4],它们反映了结构刚度和质量分布的合理性。深入分析振型和频率对结构动力性能的影响至关重要,它直接关系到悬索桥在后期运营中的安全。
为了深入分析振型和频率对结构动力性能的影响,本文以某石油管道悬索桥工程为例,采用Midas Civil有限元软件通过改变风缆的倾角角度、矢跨比、风缆截面面积以及风拉索截面面积等参数,研究这些参数对桥梁动力特性产生的影响。
1 工程概况
中缅原油、天然气管道是我国“十一五”期间规划的重大油气管道项目。管道起自缅甸西海岸马德岛,从云南瑞丽市进入中国境内。怒江跨越采用悬索形式,桁架部分总长为380 m,至东向西跨径布置为(320+2×30)m;怒江跨越主缆主跨320 m,矢高32 m,主缆矢跨比采用1/10,西岸主缆锚跨为85 m,东岸锚跨为49 m;风缆矢跨比采用1/16,如图1所示。风缆与水平面的夹角为24°,主缆直径取16 cm,有效截面积约5 203 mm2,风缆有效面积取3 200 mm2,强度安全系数均≥2.50。
2 有无风缆管道悬索桥动力特性分析
采用Midas Civil分别建立不带风缆和带风缆的管道悬索桥有限元模型,选择Lanczos迭代法进行怒江管道悬索桥结构的特征值分析,得到前10阶自振频率和振型特征,结果如表1所示。
一个结构理论上有无穷多阶固有频率,但研究人员通常只关注低阶频率,因为在与外荷载作用下的结构频率相似时,容易发生共振现象,从而导致结构破坏[5]。因此,根据表1得出关键振型频率,如表2所示。

(a) 立面

(b) 平面
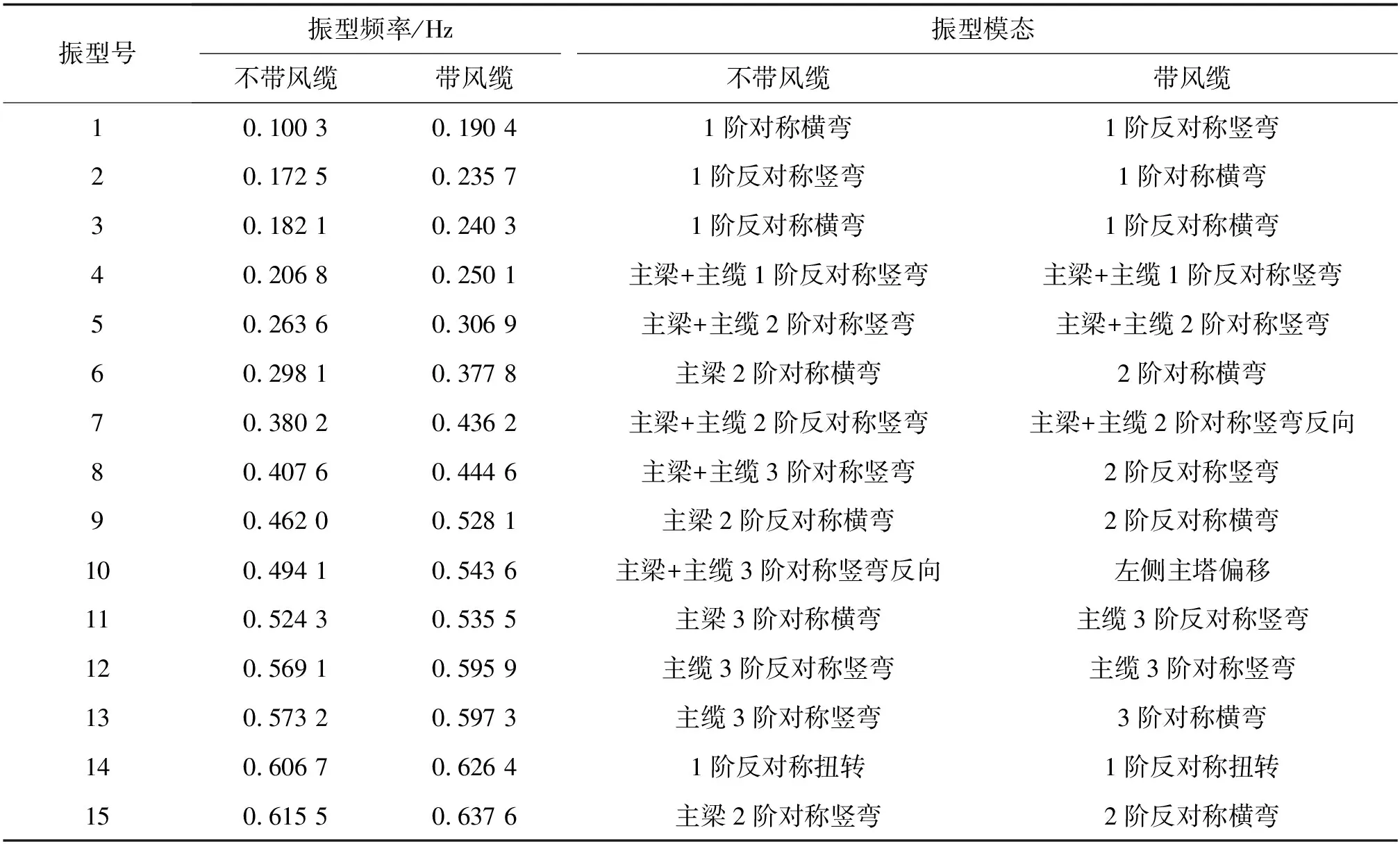
表1 有无风缆自振频率对比
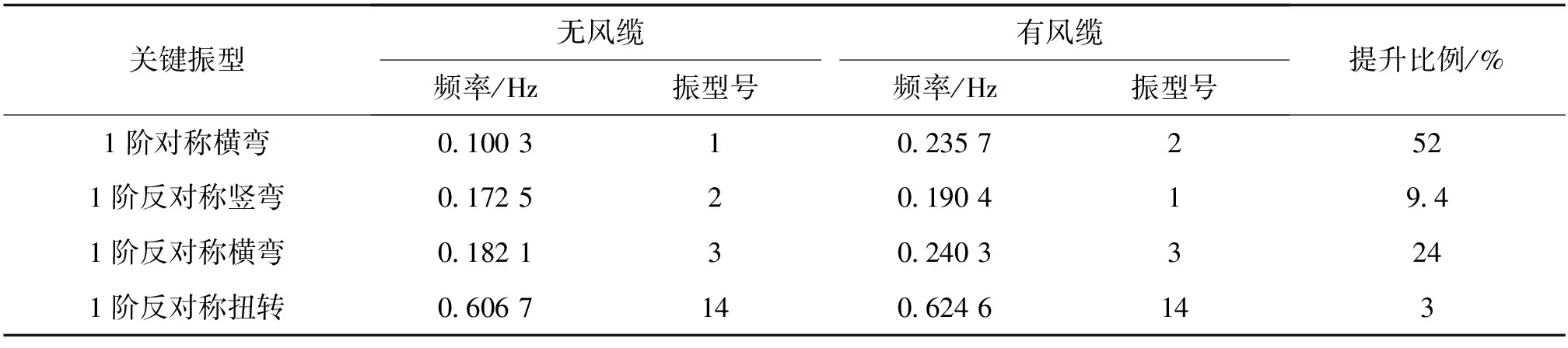
表2 有无风缆关键自振频率对比
比较表2可知,无风缆时该悬索桥第1振型就出现横向弯曲,说明横向抗弯刚度小。在加风缆后,悬索桥的横弯和竖弯的自振频率都有所提高,变化最显著的是1阶横向弯曲,提高52%,说明风缆对管道悬索桥的横向刚度影响较大。
3 成桥阶段不同风缆参数对桥梁动力性能影响
由于风缆对管道悬索桥的横向刚度影响较大,因此,分别研究风缆矢跨比、角度、截面面积等参数对成桥阶段结构动力性能的影响。
3.1 不同风缆角度对结构动力性能影响
通过分析不同水平角度的风缆引起的结构自振频率,得到前20阶振型的关键振型,结果如表3和图2所示。
由表3和图2可知,在其他参数不变的情况下,随着风缆与水平夹角的增大,1阶反对称横弯频率降低47%,1阶对称横弯降低13.1%,1阶横弯频率均逐渐减小,结构横向刚度减小,抗风稳定性能较好;竖弯频率和1阶扭转频率在逐渐增大,分别提升33%和7%。
因此,作为抵抗横向风荷载作用的风缆,应综合考虑横、竖向和扭转频率,在地势允许的情况下,选择风缆角度小,即认为15°~30°之间的风缆夹角为较优选择,且此角度的风缆外形也较为美观。
3.2 不同矢跨比风缆对结构动力性能影响
在悬索桥结构中,矢跨比既是一个非常关键的结构参数,又是一个很重要的经济因素,其变化直接影响结构受力特性、刚度变化和建设成本。赵小潘[6]曾提到工程中风缆矢跨比从1/10~1/20均有运用。通过分析不同矢跨比值的风缆引起的结构自振频率,得到前20阶振型的关键振型,结果如表4和图3所示。
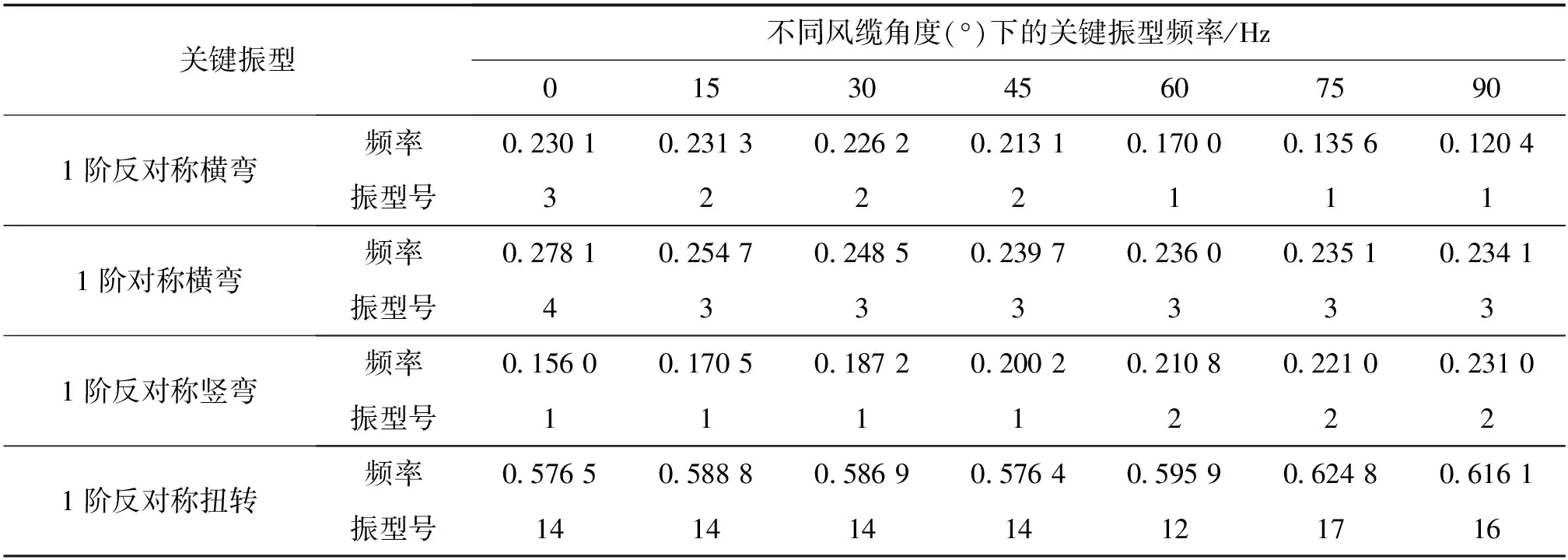
表3 不同风缆角度关键振型频率

图2 不同风缆角度关键振型频率
由表4和图3可知,在其他参数不变的情况下,1阶反对称横弯频率随着矢跨比的减小而逐渐增大,提升比例为7%;1阶对称横弯频率随着矢跨比的减小而逐渐减小,减少比例为16.8%;1阶反对称竖弯频率随着矢跨比的减小而逐渐增大,提升比例为7.1%;同理,1阶反对称扭转频率随着矢跨比的减小而逐渐增大,提升比例为10.9%。

表4 不同矢跨比风缆关键振型频率
因此,降低矢跨比,可提升反对称横弯、竖弯和扭转频率,且对称横弯降低明显。综合考虑技术、经济和施工因素,矢跨比越大,主缆材料使用越多,自重越大。因此,一般选择矢跨比偏小,建议在1/15~1/16之间。
3.3 不同风拉索间距风缆对结构动力性能影响
风拉索的布置间距本质上不会改变风缆在横桥向的水平分力,但会影响施工安装的方便性和经济性,故需研究其动力特性[7]。通过分析不同风拉索间距风缆引起的结构自振频率,得到前20阶振型的关键振型,结果如表5和图4所示。

图3 不同矢跨比风缆关键振型频率
由表5和图4可知,在其他参数不变的情况下,改变风拉索间距对1阶横弯影响很小,风拉索5 m间距频率与25 m间距频率差值占0.55%,几乎可忽略不计;对1阶竖弯影响也很小,频率差值占1.6%;对1阶扭转影响相较于横、竖弯较大,频率差值约占11.6%。
因此,风拉索间距对扭转刚度有一定明显影响,对横、竖向刚度影响微小。扭转刚度要求高的可选择改变风拉索间距,但不建议将抗风拉索设置过密,既不利于施工,也不经济,故建议风拉索间距取10 m~20 m。

表5 不同风拉索间距风缆关键振型频率
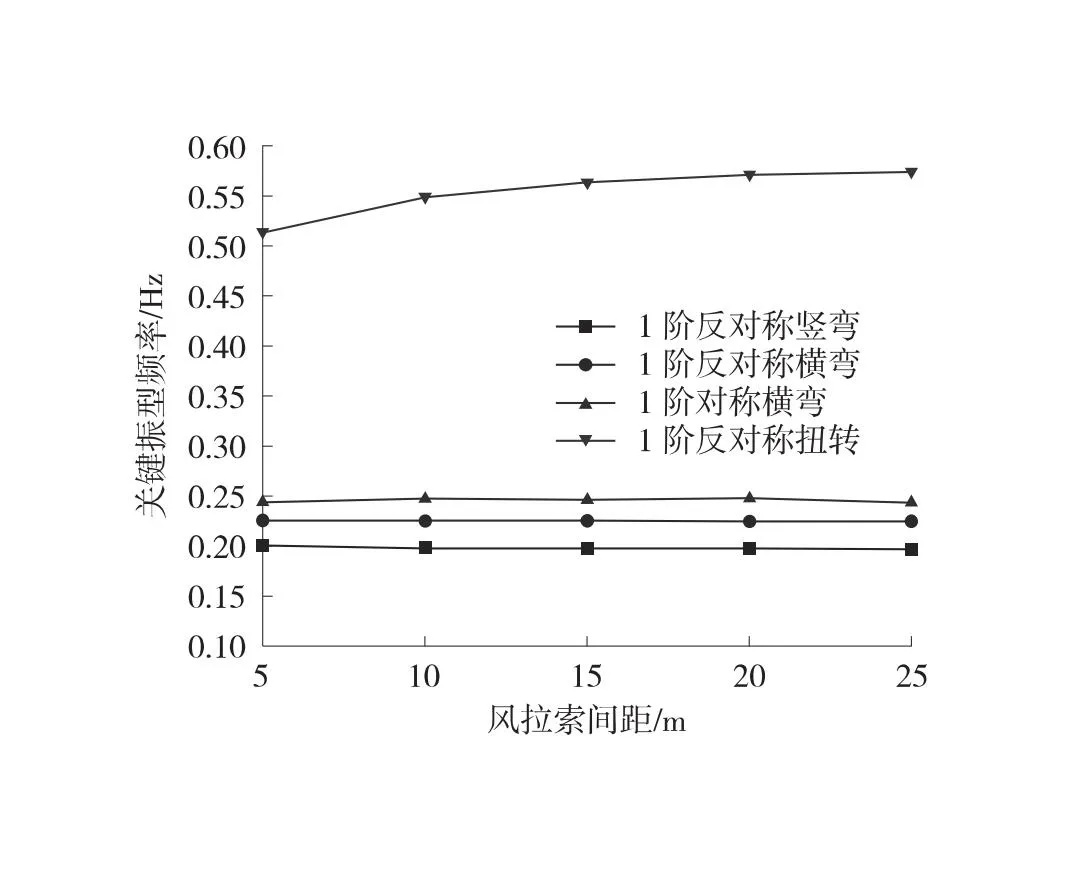
图4 不同风拉索间距风缆关键振型频率
3.4 不同截面面积风缆对结构动力性能影响
工程实践中,风缆截面面积对动力特性影响也较为显著[8],为此,只改变风缆截面面积(A),取风缆面积的0.5A、1.5A、2A、3A,通过分析不同风缆截面积引起的结构自振频率,得到前20阶振型的关键振型,结果如表6和图5所示。
由表6和图5可知,在其他参数不变的情况下,风缆截面面积(0.5A到2.5A)增大,对1阶反对称竖弯频率呈逐渐增加的趋势,提升比例为25%;对1阶反对称横弯频率呈略有增加的趋势,提升比例为16%;对1阶横弯频率也呈增加趋势,提升比例为13.7%;对1阶反对称扭转频率呈减小趋势,幅度明显,降低比例为30.5%。
综上分析,改变风缆截面积可提升横、竖向刚度,降低1阶扭转频率,影响自重。因此,还应考虑经济因素,在强度满足的情况下,建议风缆截面面积取0.5~1倍截面面积。
3.5 不同截面面积风拉索对结构动力性能影响
风拉索截面面积对结构动力特性也有一定影响,只改变风拉索截面面积,取风拉索面积的2倍、3倍、4倍,通过分析不同风拉索截面积引起的结构自振频率,得到前20阶振型的关键振型,结果如表7和图6所示。

表6 不同截面面积风缆关键振型频率

图5 不同截面面积风缆关键振型频率
由表7和图6可知,在其他参数不变的情况下,改变风拉索截面面积,对1阶横弯、1阶反对称横弯和1阶竖弯频率影响均较小,分别降低了1.9%、2.3%、0.6%,但对1阶扭转频率影响较大,降低了17.8%。
因此,风拉索截面面积对横、竖向刚度影响较小,但对扭转频率降低效果显著,结合经济和施工条件因素,且若需对结构扭转有一定要求,建议选择1倍风拉索面积。
3.6 不同跨中风拉索长度对结构动力性能影响
跨中风拉索长度对结构动力特性也有一定影响,只改变跨中风拉索长度,取跨中风拉索长度2 m、4 m、6 m、8 m,通过分析不同跨中风拉索长度引起的结构自振频率,得到前20阶振型的关键振型,结果如表8和图7所示。
由表8和图7可知,在其他参数不变的情况下,随跨中风拉索长度增加,1阶反对称竖弯、1阶对称横弯、1阶反对称横弯、1阶反对称扭转频率均呈逐渐减小趋势,分别降低了9.6%、8.5%、7%、21%。
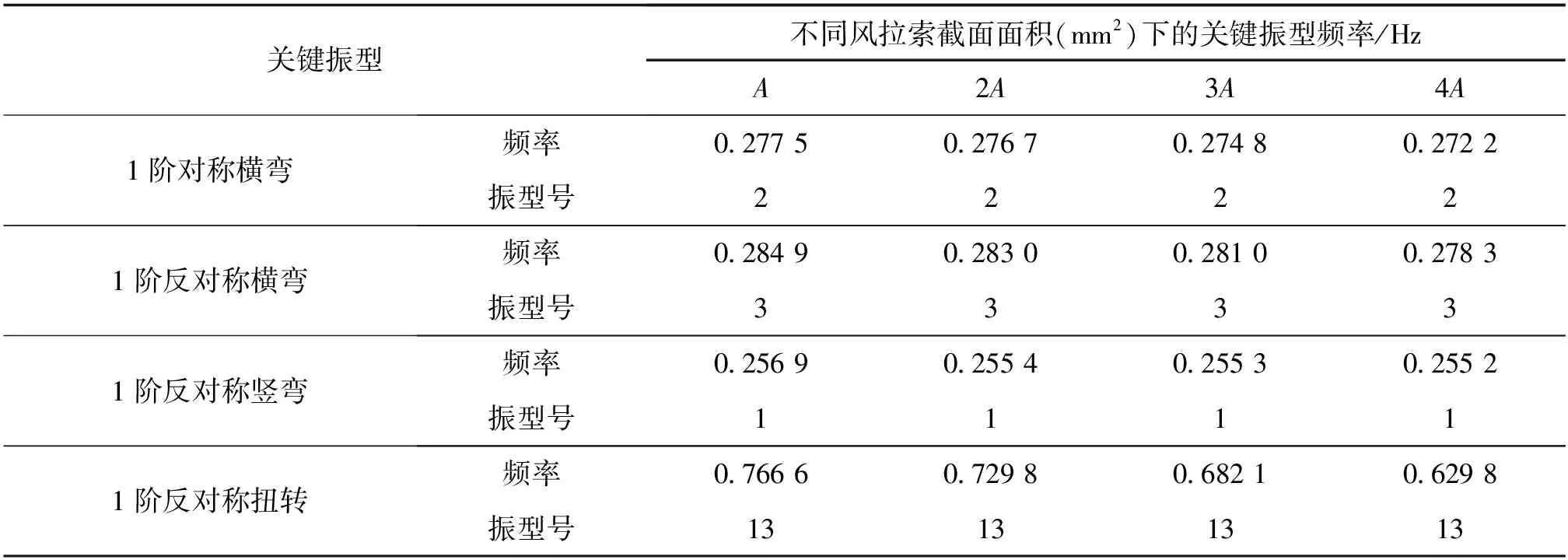
表7 不同风拉索截面面积风缆关键振型频率
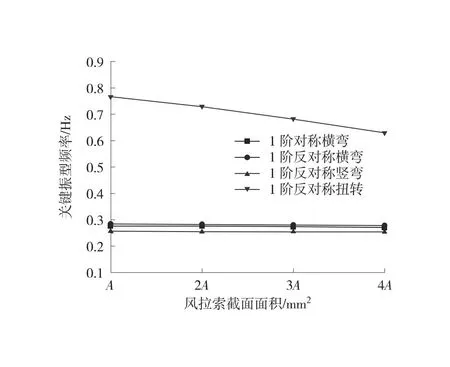
图6 不同风拉索截面面积风缆关键振型频率
因此,不同跨中风拉索长度对结构横向刚度影响较大,且对竖向刚度和扭转刚度折减比较显著,故跨中风拉索长度越小得到的频率越高,结合经济和施工条件,建议跨中风拉索长度选择1 m~3 m。
综上所述,风缆倾斜角度是对1阶横弯、竖弯频率影响最大的参数,风缆的截面面积是对1阶扭转频率影响最大的参数。
4 运营阶段不同风缆参数对桥梁动力性能影响
考虑到管道悬索桥在运营阶段油气运输过程中,结构的动力特性会有一定的改变[9],分析了管道悬索桥成桥与运营时(管道悬索桥上管道内充满石油)动力特性的变化。根据设计文件可知,怒江管道悬索桥采用直径813 mm、壁厚28.6 mm的油气运输管道,主跨径320 m,取石油原油密度0.85 kg/m3。
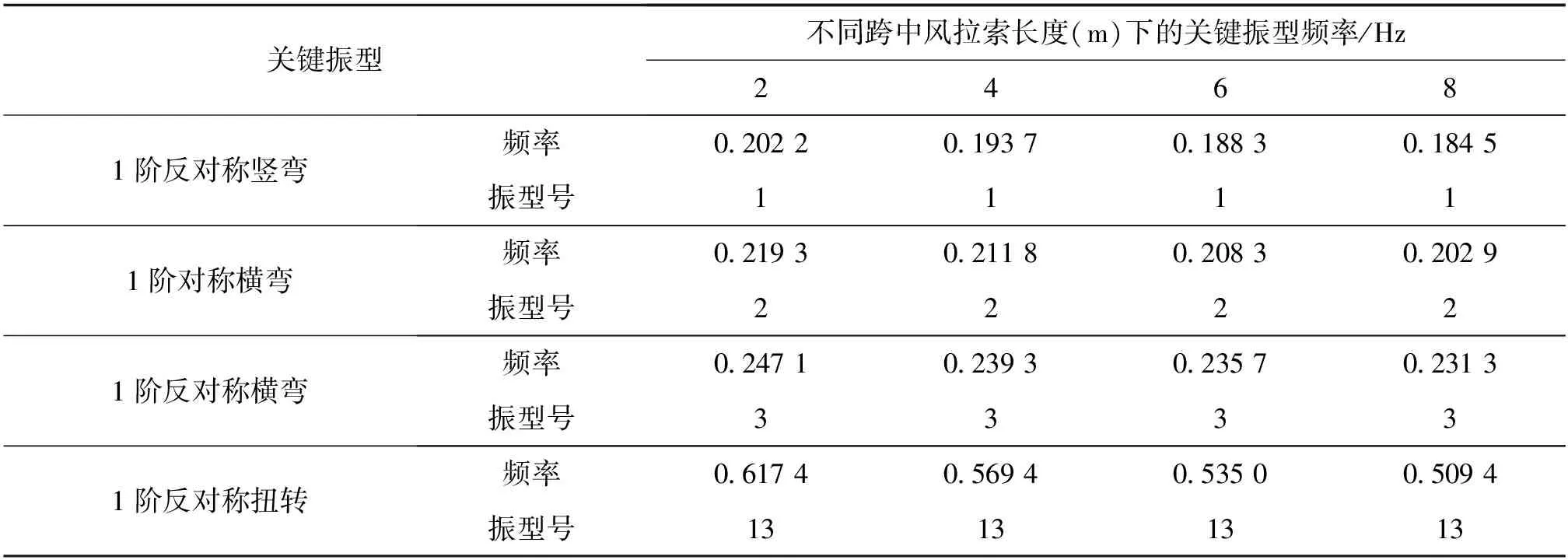
表8 不同跨中风拉索长度风缆关键振型频率
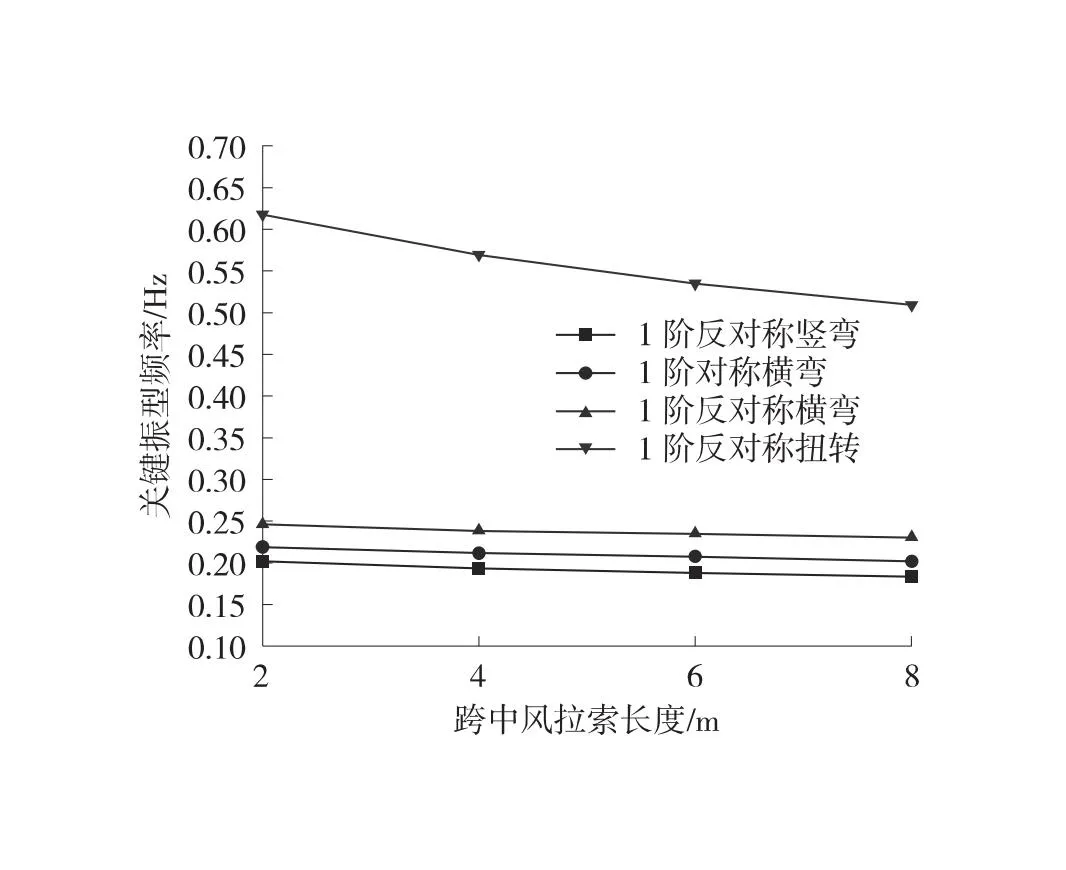
图7 不同跨中风拉索长度风缆关键振型频率
根据以上条件计算该跨管道石油重量,将该荷载加载于计算模型,并利用Midas Civil中特征值分析方法考虑油气运输时结构动力特性的变化,得到模型的关键振型频率[10-11],结果如表9和图8所示。
由表9和图8可知,运营阶段相较成桥阶段,结构1阶反对称竖弯、1阶对称横弯、1阶反对称横弯、1阶反对称扭转频率分别降低了22.5%、27.5%、24%、21.6% 。不仅竖向、扭转刚度减小,横向刚度减小也十分明显,因此可通过改变风缆参数来提高结构在运营阶段的动力特性。
根据前文对成桥阶段不同风缆参数对桥梁动力性能影响分析结果可知:风缆的倾角和面积对桥梁动力性能影响较大。因此,仅分析这2个参数对运营阶段桥梁动力特性的影响。先分析风缆倾角对结构动力特性影响,得到模型的关键1阶振型频率,结果如表10和图9所示。
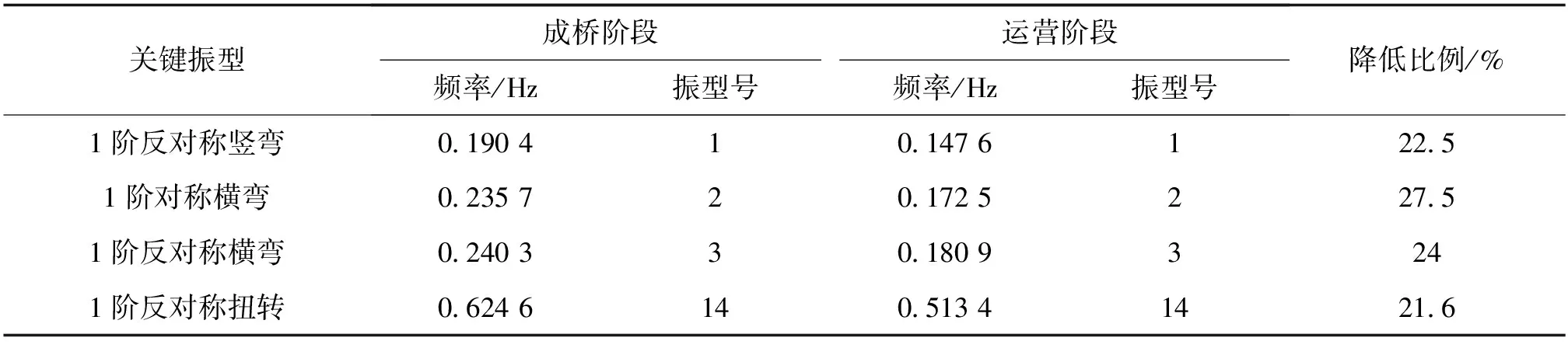
表9 成桥与运营阶段结构关键振型频率
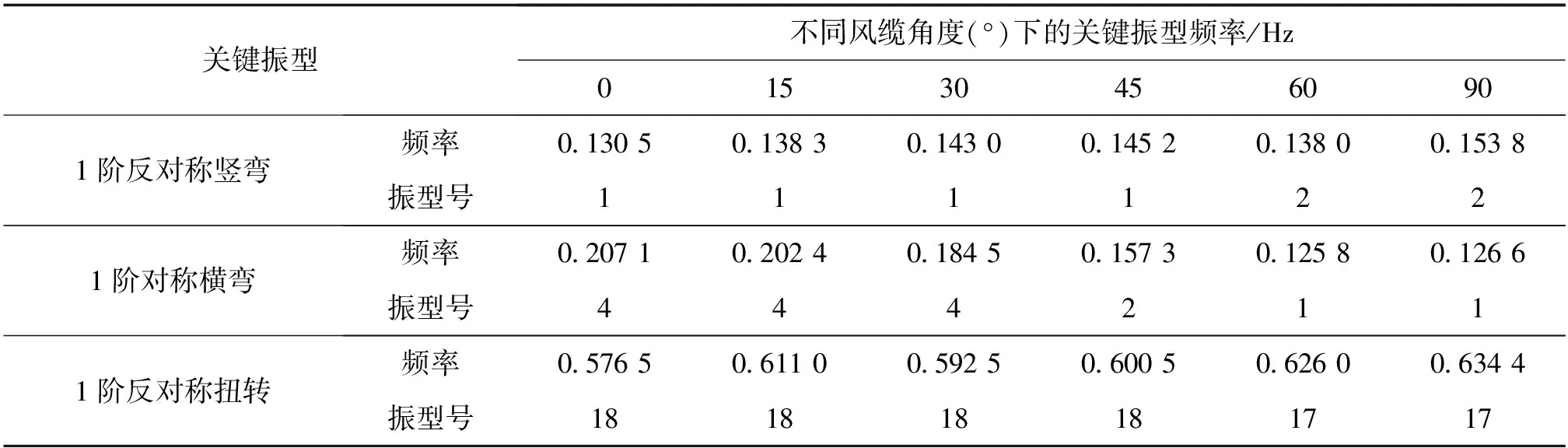
表10 运营阶段不同风缆角度关键振型频率
由表10和图9可知,运营阶段的1阶横弯频率在风缆倾角大于30°后迅速下降,造成结构横向刚度急剧不足;在保证横向刚度的前提下(取15°~30°),随风缆倾角的增大,虽然1阶竖弯及扭转频率在增加,但增值均较小,此时需改变风缆其他参数来提高其值。
分析运营阶段风缆截面面积的改变对结构的动力特性影响,得到模型的关键振型频率,结果如表11和图10所示。

图9 运营阶段不同风缆角度关键振型频率
由表11和图10可知,运营阶段的0.5倍风缆截面面积相较0.85倍风缆截面面积时的1阶横弯频率低很多,说明截面面积骤减会使得横向刚度明显减小,故不推荐将截面面积减小过多,且风缆截面面积增大会使得扭转频率急剧减小,因此,截面面积也不宜过大。此外,风缆截面面积增大时,竖向频率提升14%,但它在特征值分析中作为最初出现的模态,其频率数值很小,故需要提高竖向频率数值。
基于以上原因,推荐风缆截面面积取0.85A~A、风缆倾角取15°~30°,这就使得横向刚度得到了保证,但竖向刚度和扭转刚度仍需其他措施来进一步提升。
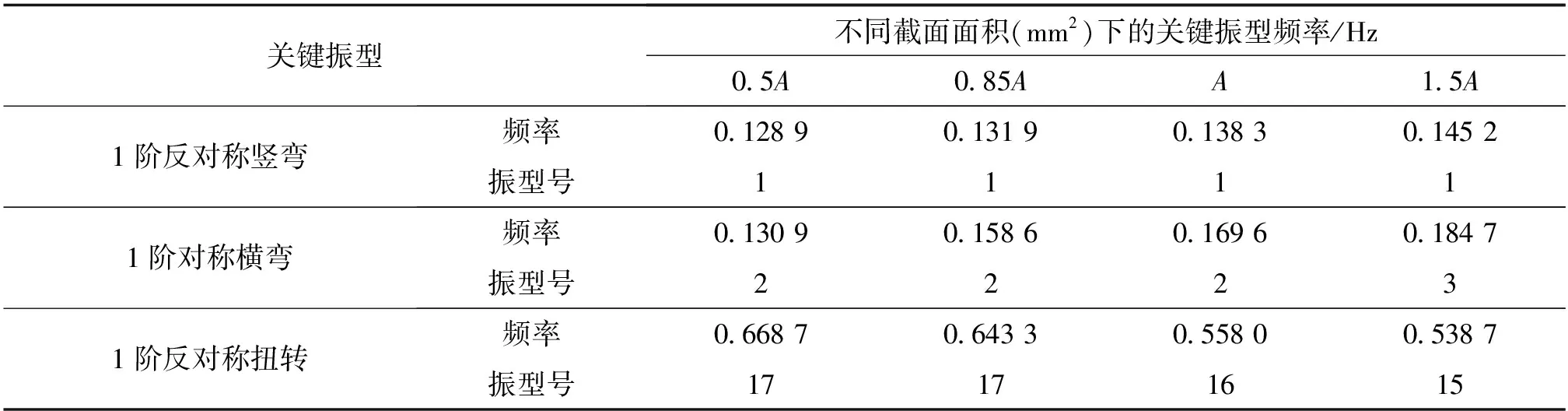
表11 运营阶段风缆不同截面面积关键振型频率

图10 运营阶段风缆不同截面面积关键振型频率
根据上述分析,选取风缆优化建议:风缆角度取15°~30°,矢跨比取1/15~1/16,风拉索间距10 m~20 m,风缆面积取0.85~1倍,风拉索面积取1倍,跨中风拉索长度1 m~3 m。
5 怒江管道悬索桥风缆参数优化
以风缆基本参数取值范围作为约束条件,风缆面积、风拉索面积和间距、风拉索长度作为设计变量,0.85A为极小值,考虑到地势原因,不改变风缆的倾角、矢跨比等参数[12-13]。风缆的主要作用是提高结构的横向刚度,则用自振频率、位移、风缆内力作为目标函数[14],在满足结构强度的情况下,对怒江管道悬索桥设计方案进行优化。共列举18种优化方案,具体方案如表12所示。
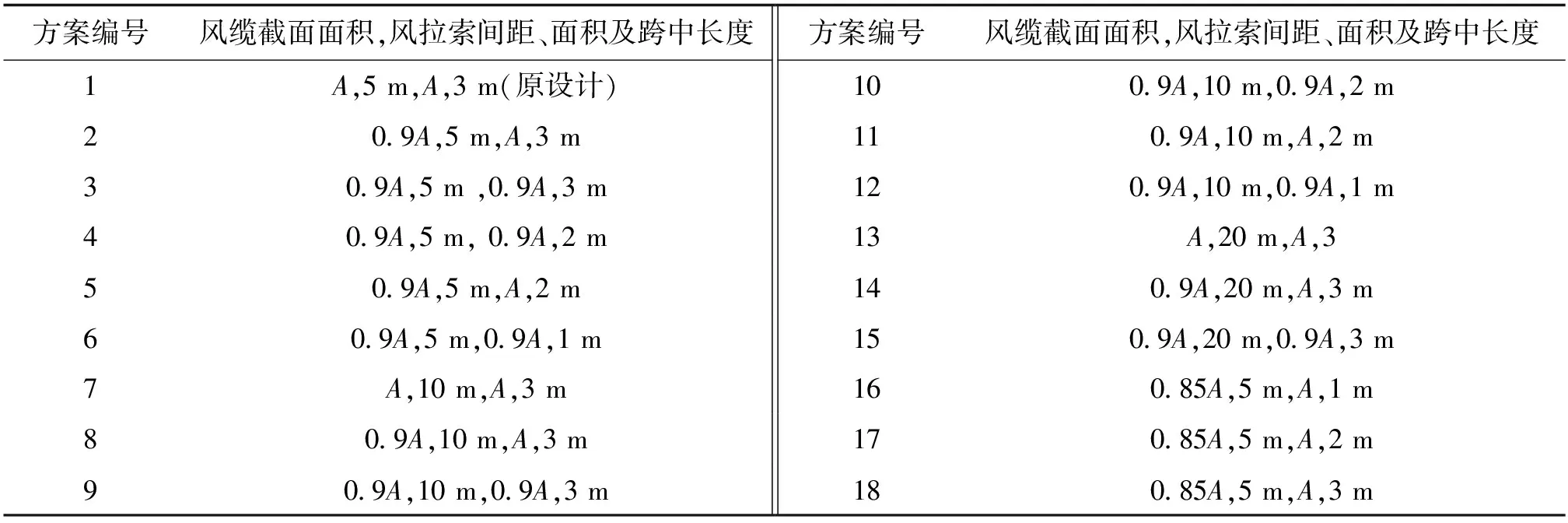
表12 风缆优化设计方案
根据以上方案建立有限元模型,并通过特征值分析方法,得到关键振型的频率,结果如表13所示。
从表13可以看出,仅有方案4、5、10、11的自振频率满足原结构的自振频率,故进一步研究各方案的位移和内力值,结果如图11所示。
从图11可以看出,方案4、5、10、11在自振频率满足的情况下,方案11结构的横向位移和风缆内力最小;方案10竖向和扭转变形最小,且横向位移和风缆内力也较小。比较方案10和方案11的经济性可知,方案11较经济,原因是风缆截面面积可降低到最小,风拉索用量减少,且其风缆内力和位移也是其他方案中最优[15]。因此,得到怒江管道悬索桥优化方案:风缆截面面积0.9倍、风拉索间距10 m、风拉索面积不变、跨中风拉索长度2 m。
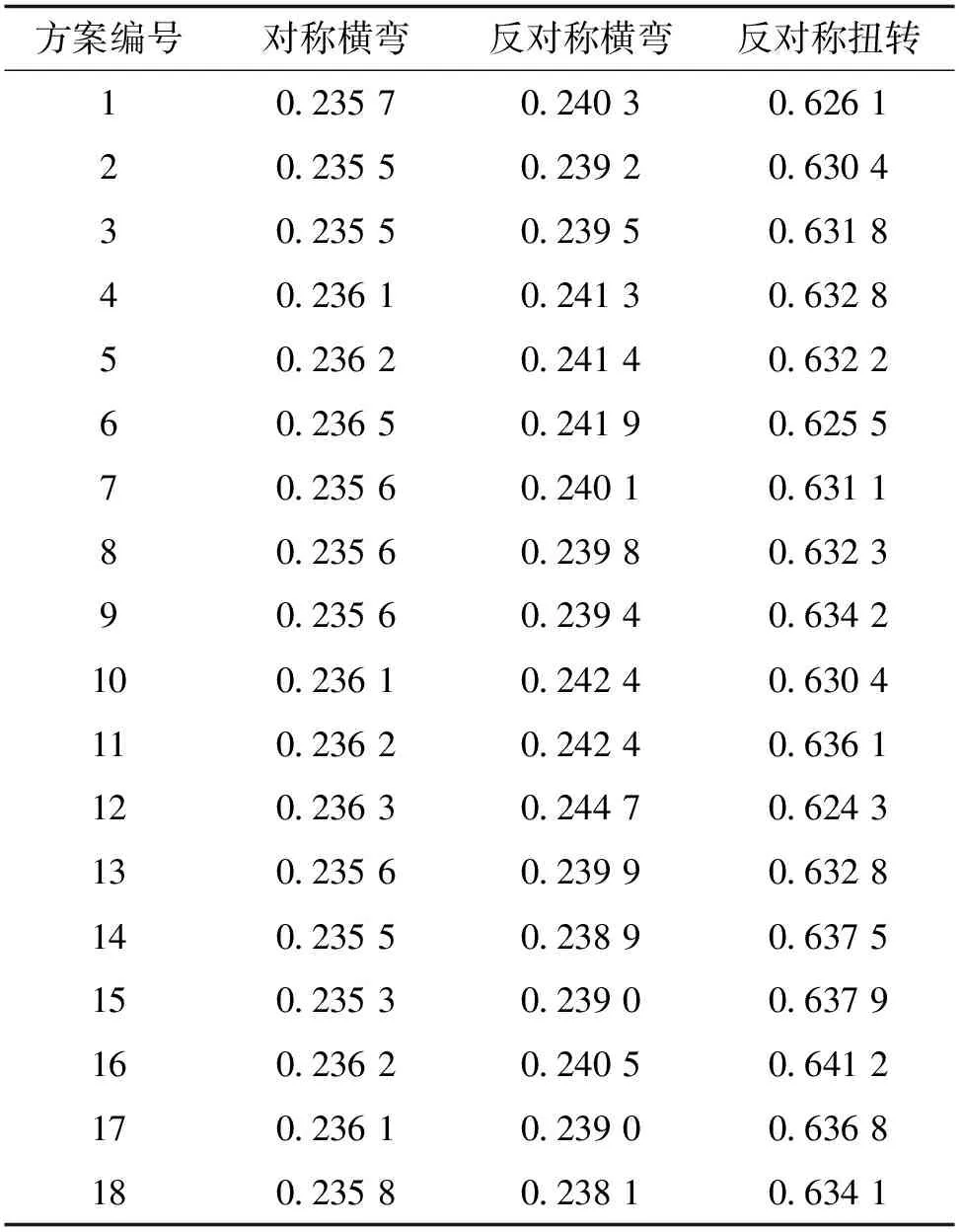
表13 风缆优化设计方案自振频率 Hz

(a) 各方案横向位移

(c) 各方案扭转变形
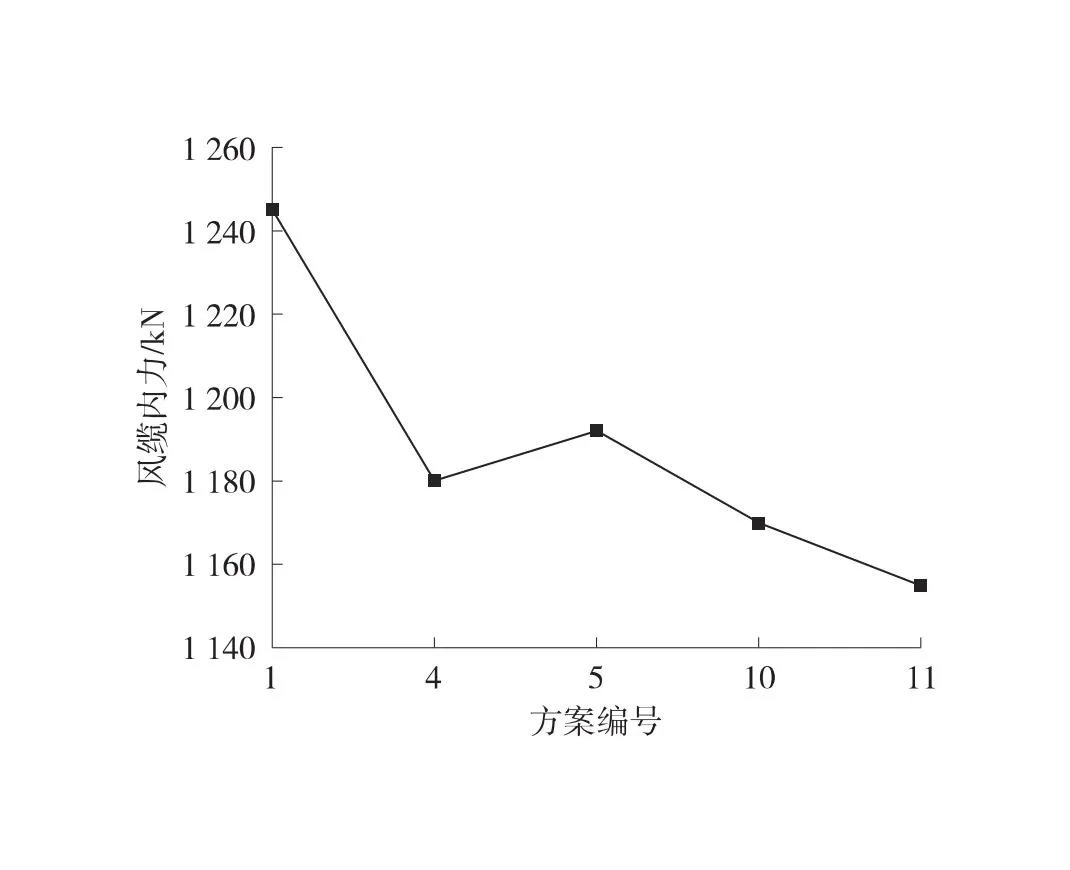
(d) 各方案风缆内力
6 结论
基于特征值分析理论和方法,研究了风缆各参数对管道悬索桥的动力特性产生的影响,并通过实例分析确定了怒江管道悬索桥风缆参数的最佳取值范围,得出如下结论:
1) 风缆倾角对1阶横弯效应影响最为显著,而风缆截面面积则对1阶竖弯和扭转效应影响最大。
2) 在管道悬索桥运营阶段,若管道的横向刚度已满足要求,则需考虑适度提升竖向和扭转方向的刚度。
3) 建议风缆的安装角度保持在15°~30°之间,矢跨比控制在1/15~1/16之间,风拉索的间距在10 m~20 m范围内,风缆截面面积可选择0.85倍至1倍,跨中风拉索的长度应在1 m~3 m之间。
