基于改进鲸鱼优化算法的移动机器人多目标点路径规划

王步伟 潘鹏程*

（三峡大学电气与新能源学院，湖北宜昌，443002）

0 引言

路径规划是移动机器人发展中至关重要的一环[1]，它可以提高任务完成的效率并降低成本。针对路径规划的传统算法有快速搜索随机树（Rapidly-exploring Random Tree, RRT）算法[2]、A* 算法[3]和Dijkstra 算法[4]等。传统路径规划算法往往仅适用于单个目标点的任务中，而在物流配送、无人机巡检、机器人导航和公共交通规划等问题中，往往需要在一个给定的环境中找到一条连接多个目标点的路径，即多目标点路径规划。因此，为解决多目标点路径规划问题，需要使用优化算法寻得一条遍历所有目标点的最短路径，如粒子群优化（Particle Swarm Optimization, PSO）算法[5]、灰狼优化（Grey Wolf Optimization, GWO）算法[6]和鲸鱼优化算法（Whale Optimization Algorithm, WOA）[7]等。

鲸鱼优化算法是一种新型的生物启发式优化算法，受到座头鲸捕食行为的启发，通过模拟鲸鱼的捕食策略和社会行为来求解优化问题。WOA 的主要优点是全局搜索能力强，收敛速度快，并且能很好地平衡探索与开发能力，因此广泛应用于函数优化、机器学习与路径规划等领域。与此同时，国内外研究者针对标准WOA 的不足之处也提出了多种改进[8-9]。杨炳媛等[10]提出了根据个体的集散程度自适应选择全局搜索或局部搜索的方法，以实现WOA 的快速收敛；尹梅等[11]则通过采用自适应收敛因子来平衡算法的探索和开发能力。在处理多目标点路径规划等复杂问题时，标准鲸鱼优化算法仍存在搜索精度不足，以及收敛速度较慢的问题。

针对以上问题，本文提出一种改进的鲸鱼优化算法：引入自适应搜索控制系数和记忆库列表策略提高算法收敛速度、精度和搜索能力，并与A*算法相结合，将A*算法单目标点路径规划生成的实际距离矩阵作为输入，从而提高多目标点路径规划的精度和效率。

1 环境建模

栅格地图的建模方法[12]具有地图构建简单、位置精度高、效率高等优点。假定环境地图长为,宽为，将地图平均划分为个长宽相等的小栅格，用表示每个小栅格，整个地图可用表示：

每个栅格有无障碍物信息表达式为：

如图 1 所示，黑色部分表示障碍物，白色部分表示可自由通过区域。机器人在栅格地图内采用8 邻域[13]的搜索方式，红色箭头为可行走的8 个方向。

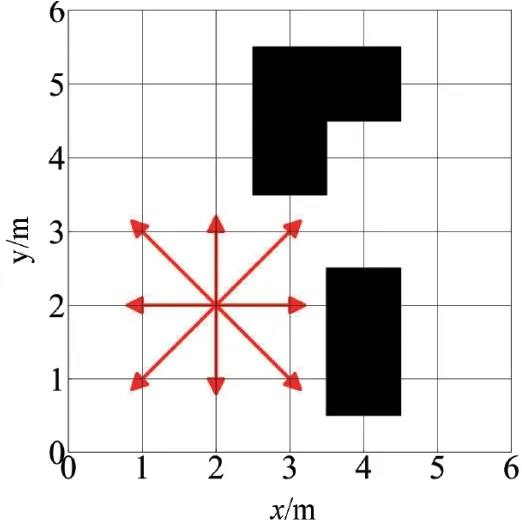
图 1 栅格地图模型

2 路径规划

2.1 单目标点路径规划

单目标点路径规划问题可表述为：为移动机器人在环境中寻找一条无碰撞、效率高且长度最短的路径。

A*算法是一种基于传统图搜索的智能启发式算法，它具有稳定性高、节点搜索效率高等优点[14]，因此普遍用于单目标点路径规划。主要原理为：以起点作为初始节点，搜索初始节点旁8 个邻域，并通过启发函数评估后选择代价最小的节点，然后搜索这个节点的8 个邻域，选择下一个代价最小的节点，重复上述步骤，直到选择的节点与目标点重合。最后，将这些代价最小的节点连接起来，便得到了一条最优路径。A*算法的代价函数如下：

图 2 A＊算法示意图

由于A*算法充分考虑了障碍物对路径的影响，更符合机器人的实际运行，故本文使用A*算法生成所有目标点之间的距离矩阵，表达式为：

2.2 多目标点路径规划

在规划过程中，需要考虑移动机器人在障碍环境下的移动限制，通过使用 A*算法计算出的最短避障距离替换忽略障碍物的欧式距离，确保在有障碍物的场景下为移动机器人规划出的路径与实际最优路径一致。本文旨在，结合A*算法的单目标点路径规划和鲸鱼优化算法的多目标点优化，使得值最小。

3 鲸鱼优化算法

在搜索最优解过程中，标准鲸鱼优化算法有包围猎物、随机搜索、螺旋捕猎3 种行为方式可供选择。

3.1 标准鲸鱼优化算法

3.1.1 包围猎物行为

鲸鱼优化算法假设当前种群中最优解为猎物位置或已接近目标猎物的位置，种群中其他鲸鱼个体根据当前最优解更新自身位置。包围猎物的过程可用数学模型表示为：

3.1.2 随机搜索行为

鲸鱼种群根据自己当前的位置、全局最优解和一定的随机性来更新自己的位置，使得鲸鱼能够在搜索空间中以一定的概率跳出局部最优解，从而提高搜索到全局最优解的可能性。采用随机搜索行为的条件是，可以用模型表示为：

3.1.3 螺旋捕猎行为

当鲸鱼靠近全局最优解时，它们会以螺旋的方式在局部范围内进行搜索。螺旋行为的策略是在当前位置和全局最优解的位置之间生成一个螺旋路径，然后鲸鱼沿着这个路径进行移动。这样可以使得鲸鱼在靠近全局最优解的过程中，更好地探索局部解空间，提高找到更优解的概率。螺旋捕猎行为可用数学模型表示为：

3.2 改进鲸鱼优化算法

3.2.1 自适应搜索控制系数

在标准鲸鱼优化算法中，系数向量为均匀分布在[0,2]内的随机数，是一个控制搜索速率的参数，故值是在每次迭代时随机生成的，这可能导致搜索行为较为随机，无法充分平衡算法全局搜索和局部搜索的能力，从而导致收敛精度不足。因此，本文提出一种自适应搜索控制系数，根据迭代次数来动态调整的大小，表达式如下：

3.2.2 记忆库列表策略

在处理高维度或复杂问题时，WOA 的收敛速度较慢，仅靠三种位置更新机制已难以在迭代后期使算法跳出局部最优。因此，本文在鲸鱼优化算法中添加一个记忆库列表，使算法能够记录迭代过程中遇到过的当前最优解。达到最大迭代次数后，将最后一次迭代得到的最优解与记忆库中的解进行比较，选取较优解作为最终结果，从而有效提高算法所得解的适应度，步骤如下：

1）在鲸鱼种群初始化完成后建立一个记忆库列表，用于储存当前最优解。

2）将每次迭代后的最优解加入到记忆库中，避免记忆库容量过大，限制记忆库列表长度，当达到最大容量时，使用和函数移除最差的解：

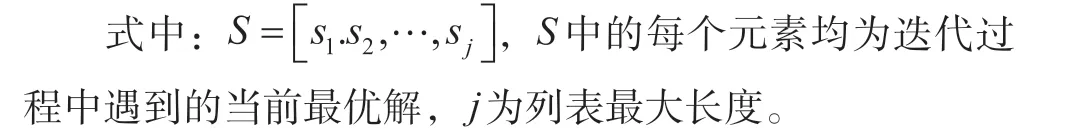
3）将最终解与记忆库列表的最优解进行比较取较优解。

3.3 算法性能测试

为了验证改进鲸鱼优化算法的性能，本文选取4 个常用的标准测试函数对WOA 与本文算法的搜索精度以及效率进行比较，种群数量为30，函数维度为30，迭代次数为500。如表 1 所示，、为单模态测试函数，在搜索空间中只有一个全局最小值；、为多模态测试函数，在搜索空间中有许多局部最小值和一个全局最小值。两种算法收敛精度对比如表 2所示， 收敛速度对比如图 3所示。

表 1 测试函数

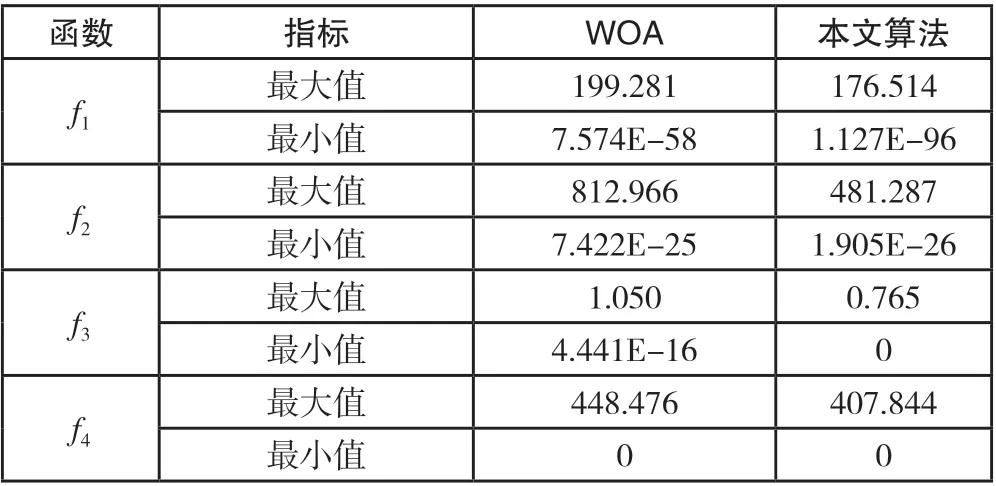
表 2 算法收敛精度对比

图 3 算法收敛速度对比

3.4 多目标点路径规划步骤

本文基于改进鲸鱼优化算法的多目标点路径规划步骤如下：

1）构建栅格地图，设定初始参数：鲸鱼种群数量、最大迭代次数，确定所有目标点坐标；

6）达到最大迭代次数后，将最终解与记忆库列表中的最优解进行比较，取较优解作为最优遍历顺序；

7）根据步骤6）所得最优遍历顺序生成最优多目标点路径规划图。

4 仿真实验与分析

为验证本文所提改进鲸鱼优化算法的性能，在处理器为Intel(R) Core(TM) i5-8300H CPU @ 2.30GHz、运行内存为16GB 的计算机上，利用Pycharm 平台进行仿真实验，python 版本为3.10。在相同地图环境下对粒子群算法、标准鲸鱼优化算法以及本文改进鲸鱼优化算法进行仿真对比，种群数量均设为30，迭代次数设为500。

4.1 简单场景下的仿真对比实验

为验证本文改进鲸鱼算法在简单场景下多目标点路径规划的精确度与收敛速度，在场景中选取9 个目标点进行规划，首先使用A*算法获得距离矩阵，然后分别使用三种优化算法获得遍历顺序列表，如表 3 所示。规划结果如图 4 所示，图中蓝色五角星为目标点，黑色矩形为障碍物，红色线条为算法所规划的路径。算法迭代曲线如图 5 所示，算法性能对比如表 4 所示。

表 3 简单场景下三种算法遍历顺序对比

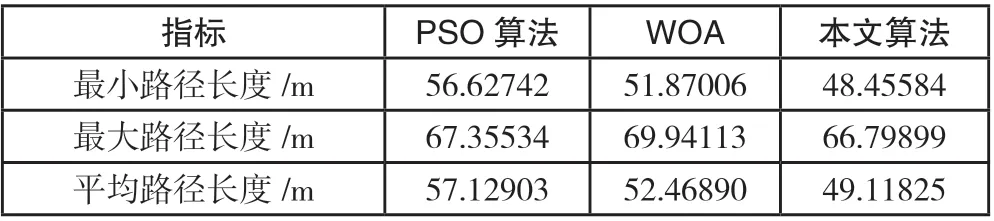
表 4 简单场景下三种算法路径长度对比

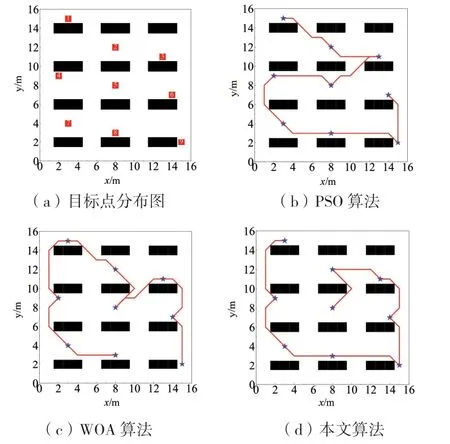
图 4 简单场景下三种算法路径规划结果

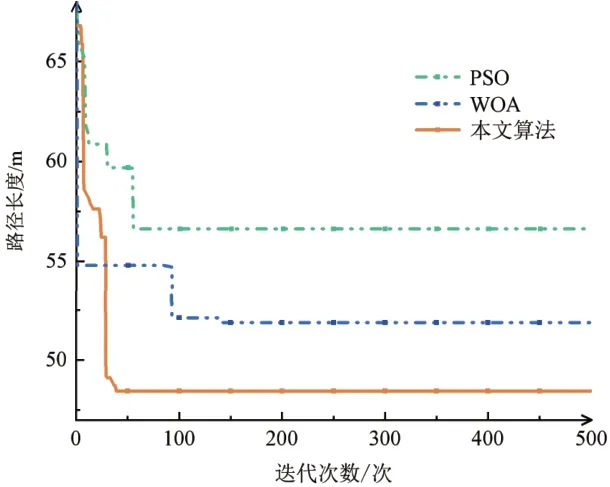
图 5 简单场景下三种算法迭代曲线

由图 4 以及表 4 中数据可知，本文改进鲸鱼优化算法相比于PSO 算法和WOA，最小路径长度分别减少14.43%、6.58%，平均路径长度分别减少14.02%、6.39%。由图 5 可知，PSO 算法收敛速度优于WOA，但由于过早陷入局部最优，导致路径长度不如预期。WOA 虽然在中途陷入局部最优，得益于其随机搜索行为，在迭代100次左右跳出局部最优解，但最终导致WOA 收敛速度变慢。本文所提出的改进鲸鱼优化算法采用了自适应搜索控制策略和记忆库列表策略，在收敛速度和路径长度方面，改进鲸鱼优化算法均表现出优于PSO 算法和WOA 的性能。这说明本文的改进方法在解决简单场景下多目标点路径规划问题时具有更高的效率和准确性。

4.2 复杂场景下的仿真对比实验

为验证本文改进算法在复杂场景下的性能，在复杂场景1 下取13 个目标点进行规划，在相同仿真条件下，同样对比三种算法的性能。遍历顺序对比如表 5 所示，规划结果如图 6 所示，算法迭代曲线如图 7 所示，算法性能对比如表 6 所示。

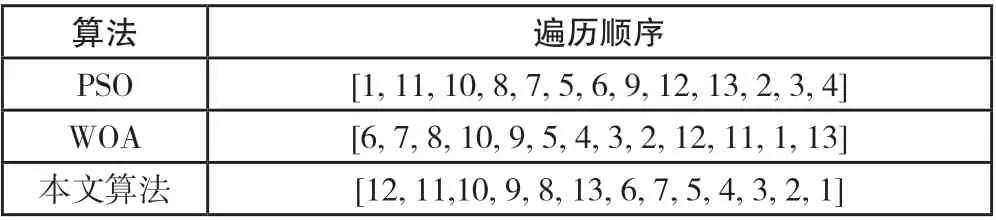
表 5 复杂场景1 下三种算法遍历顺序对比

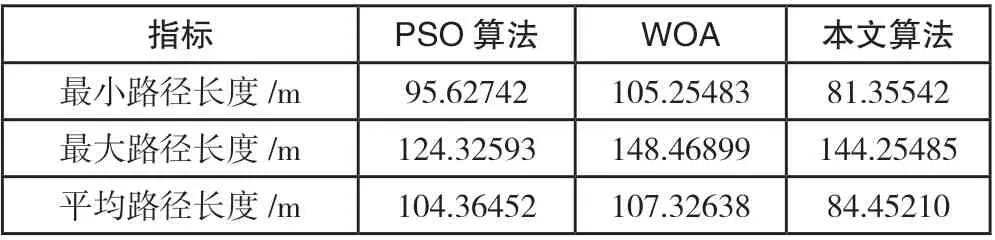
表 6 复杂场景1 下三种算法路径长度对比

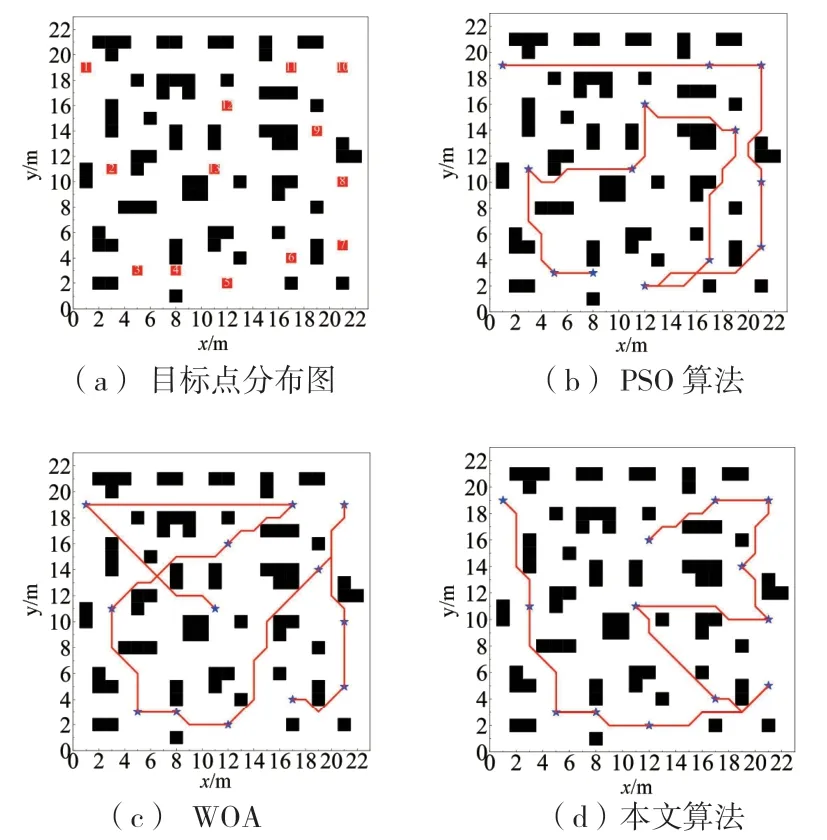
图 6 复杂场景1 下三种算法路径规划结果

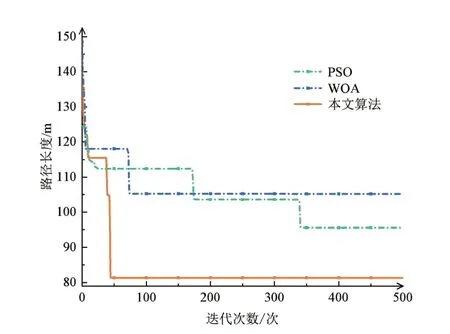
图 7 复杂场景1 下三种算法迭代曲线

由图 6 以及表 6 中数据可知，在复杂场景1 下，本文改进鲸鱼优化算法相比于PSO 和WOA，最小路径长度分别减少14.92%、22.71%，平均路径长度分别减少19.08%、22.31%。由图 7 可知，在复杂度更高的场景中，三种算法均可能陷入局部最优解。WOA 在迭代后期难以跳出局部最优解，导致生成的路径存在过多交叉，并且最小路径长度不如预期。PSO 算法虽然两次跳出局部最优解，但其收敛速度较慢。相对而言，本文所提出的算法在迭代初期也可能陷入局部最优解，然而通过引入记忆库列表策略，使算法能够迅速摆脱局部最优解，在50次迭代内便完成了收敛。

为进一步验证本文改进算法在复杂场景下的性能，在复杂场景2 下取16 个目标点进行规划，在相同仿真条件下，同样对比三种算法的性能。遍历顺序对比如表 7所示，规划结果如图 8 所示，算法迭代曲线如图 9 所示，算法性能对比如表 8 所示。

表 7 复杂场景2 下三种算法遍历顺序对比

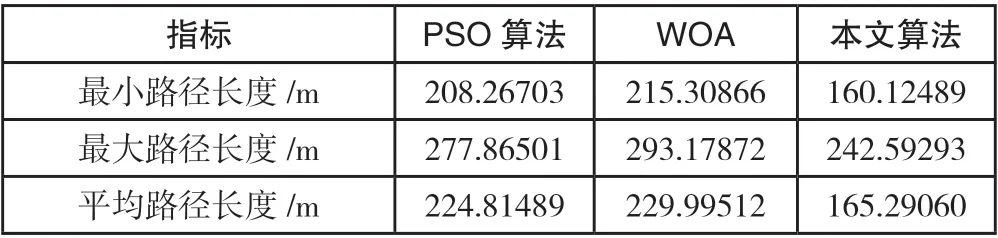
表 8 复杂场景2 下三种算法路径长度对比

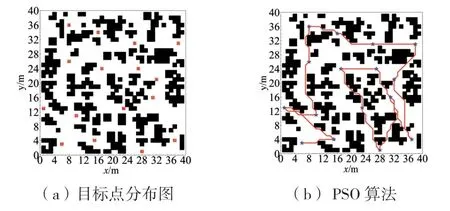
图 8 复杂场景2 下三种算法路径规划结果

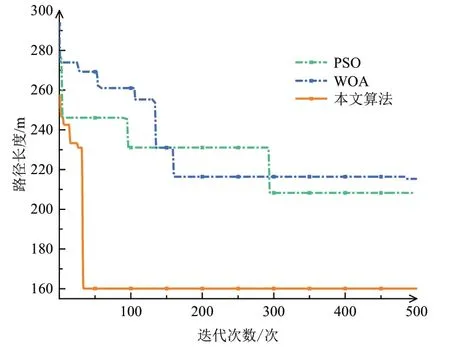
图 9 复杂场景2 下三种算法迭代曲线

由图 8 以及表 8 中数据可知，在复杂场景2 下，本文改进鲸鱼优化算法相比于PSO 算法和WOA，最小路径长度分别减少23.12%、25.63%，平均路径长度分别减少26.48%、28.13%。由图 9 可知，PSO 算法和WOA 均陷入多次局部最优，导致最小路径长度不如预期。而本文算法在收敛速度以及路径长度方面均优于其它两种算法，具有较好的鲁棒性。

5 结论

本文针对移动机器人多目标点路径规划存在效率不高、准确性较低的问题，提出一种改进鲸鱼优化算法来改善上述不足：

1）通过引入自适应搜索控制系数，提高了算法平衡全局搜索和局部搜索的能力；

2）提出一种记忆库列表策略，通过增加记忆库列表存储最优解并进行维护更新，从而提高了算法所得解的质量并降低陷入局部最优的概率。

最后，在python 编程环境下，对 PSO 算法、WOA 以及本文算法进行仿真对比实验。研究结果表明，随着场景复杂度的增加，本文算法相较于WOA 所得出的最小路径长度分别减少6.58%、22.71%、25.63%，相较于PSO算法所得出的最小路径长度分别减少14.43%、14.92%、23.12%。

综上所述，场景复杂度越高，本文提出的算法相较于其他两种算法展现出更为显著的优势。因此，本文改进算法实现了路径规划效率和准确性的双重优化，对移动机器人的多目标点路径规划有着重要意义。将本文提出的新方法应用到多机器人的多目标点路径规划是下一步的研究内容。