基于支持向量回归模型的机器人误差补偿算法

肖文磊 姚开然 涂志健 齐琦 孙子惠 于奚振 张煌

（1北京航空航天大学机械工程及自动化学院，北京，100191；2芜湖赛宝机器人产业技术研究院有限公司，安徽芜湖，241000）

0 引言

随着制造企业智能化发展，以及对智能化程度要求的不断提升，工业机器人在数控加工中的应用也越来越普及。传统的工业机器人一般采用人工示教的方法确定所处位置，这种方法高度依赖机器人的重复定位精度，应用场景多为简单的工业应用，无法满足复杂加工任务。主流的、基于CAD 软件的机器人离线编程方式又需要很高的绝对定位精度，如果机器人末端位置偏差较大，会导致离线编程与实际加工现场不符合。为此，亟需开展工业机器人绝对定位精度的相关研究。

基于模型对机器人进行校准是提升工业机器人绝对定位精度的有效手段。ROTH[1]将机器人标定分为关节标定、运动学标定以及非运动学标定。机器人校准方法可以分为基于模型的校准和无模型校准。基于模型的校准是建立机器人的运动学模型，并对其中的运动学参数进行辨识。相关经典工作包括DANEVIT 和HARTENBERG[2]提出的DH 参数法，HAYATI[3]提出的MDH 法，STONE[4]、ZHUANG[5]等提出了连续参数模型等。由于DH 参数法及其衍生方法都是利用齐次矩阵对机器人各关节间位姿变换建模，随着机器人关节增加，建模会相当复杂，不利于求解。近年来，基于李代数的指数积方法逐渐流行，代表性工作包括BROCKETT[6]的机械臂指数积运动学方程（POE），CHEN[7]提出的本地POE建模校准方法等。

上述基于模型的校准主要用于解决机器人几何误差问题，对于非几何误差，主流方法包括有限元法、虚拟关节法等。另外，对于复杂的非几何误差建模，主要采用真实数据集和神经网络相结合的方式拟合非几何误差，包括深度神经网络[8]、径向基函数（RBF）神经网络[9]等。但全空间采用神经网络训练较为复杂且精度不高，因此有学者提出直接对机器人工作空间误差进行插值计算。周炜[10]提出了空间插值立方体划分，MA[11]利用切比雪夫多项式对机器人的关节转角误差进行拟合，ALICI[12]利用傅里叶多项式直接对空间误差进行拟合。

本文搭建了支持向量回归（Support Vector Regression,SVR）模型，通过向模型输入机器人末端的理论位置，从而预测机器人末端补偿量；在模型训练过程中，采用粒子群优化（Particle Swarm Optimization, PSO）算法对模型的部分参数进行了优化，提升了模型的预测精度。

1 PSO-SVR 预测模型

SVR 算法的数学形式可以表述为：

图1 为特征量为1 时的SVR 算法示意图。

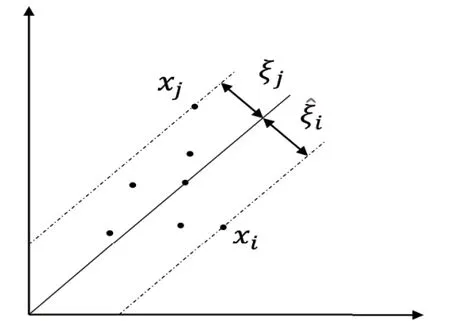
图1 SVR 算法示意图

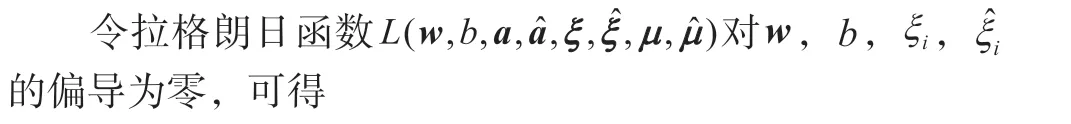
将式（7）—式（10）带入式（6）的拉格朗日函数中，即可得到SVR 模型的对偶问题：

常用的核函数包括多项式核函数、径向基核函数和sigmond 核函数。其中，径向基核函数能够较好地适应非线性问题，因此，本文选取径向基核函数作为模型中的核函数。径向基核函数的函数表达式为：

2 误差补偿算法

采用SVR 算法对机器人误差进行预测分为三步：

1）获取训练集。

在机器人的工作空间内选择多个随机点位。对于每一个随机点位，将该点位作为目标位置输入至机器人控制器，待机器人行走完成后，由激光跟踪仪测量出机器人末端实际位置与理论位置之差，驱动机器人对点位差值进行补偿。待补偿结束后，激光跟踪仪再次测量末端实际位置与理论位置之差，迭代上述过程。如此反复，直到机器人末端实际位置与理论位置之差小于0.05mm。这一步被称作迭代闭环补偿。在针对每一个随机点位的实验过程中，记录机器人的理论位置，并将其作为模型输入，机器人实际补偿指令的总和作为模型输出，如此构成训练集。

2）训练模型。

将训练集放入SVR 模型中进行训练。在本研究中，优化过程采用PSO 算法实时优化调整SVR 模型中的参数和。

3）模型验证。

类似于步骤1），重新在机器人的工作空间选取多个随机点位。对于每一个随机点位，将其作为目标位置驱动机器人行走，并对其进行精度小于0.05mm 的迭代误差补偿，记录下迭代误差补偿指令的总和，作为真实补偿量。而后，重新将点位作为目标位置驱动机器人行走，并以点位位置作为模型输入，输入至训练出的SVR 模型，得到模型输出，也就是SVR 模型计算所得的补偿量，称之为预测补偿量。将该补偿量与真实补偿量进行对比，验证模型有效性。

SVR 算法的流程图如图2 所示。

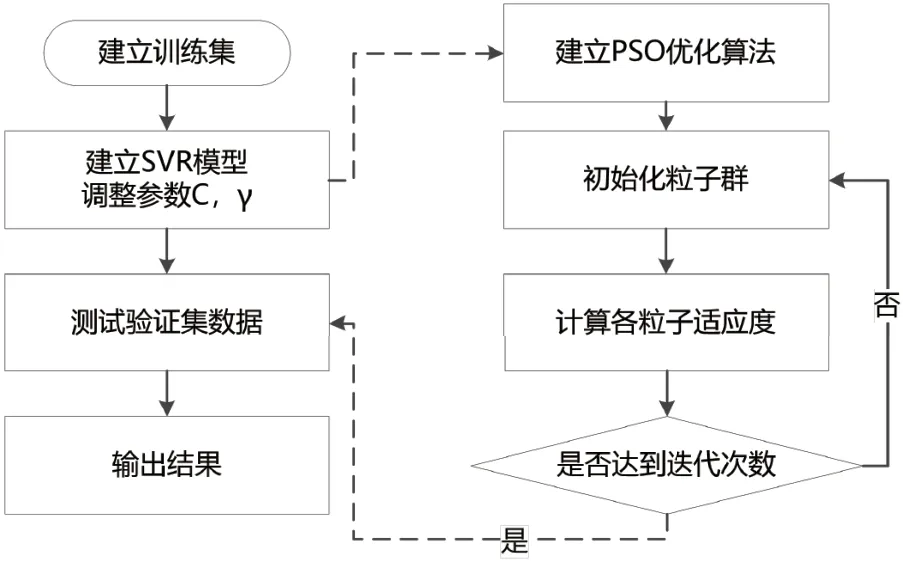
图2 SVR 算法的流程图

从模型，即式（11）可以看出，SVR 模型是一种多输入单输出模型。由于机器人末端点位存在3 个XYZ 自由度，因此需要训练3 个SVR 模型，每个模型均以机器人的初始位置作为模型输入，三个方向上的预测补偿量作为模型的输出。

3 模型训练结果以及实验验证

3.1 实验设备

为了提供模型训练的数据集以及进行实验验证，本研究搭建了基于激光跟踪仪的机器人位置测量系统，系统实验现场如图3 所示。该系统主要由工业机器人、TwinCAT 主站和激光跟踪仪构成。系统拓扑与通讯协议如图4 所示。

图3 系统实验现场

图4 系统拓扑与通讯协议

工业机器人的型号为KUKA KR6 R700 sixx，其控制箱内部的Beckhoff 模块EL6695 可作为网桥，可通过E-bus和EtherCAT 总线连接工业机器人控制器以及TwinCAT 主站，实现两者之间的信息交互。KUKA 机器人控制箱内部搭载有MxAutomation 软件模块，该模块为TwinCAT 主站提供了机器人监控接口。

激光跟踪仪的型号为Leica AT901，通过TCP/IP 与TwinCAT 主站通讯，可实时测量机器人末端的位置。TwinCAT 主站在接收到激光跟踪仪的数据包后，实时对数据包进行解析，从而得到机器人末端的位置数据。

3.2 PSO-SVR 模型训练

在机器人空间中选取500mm×200mm×150mm 矩体范围，在其中随机采样200 个点作为数据集。选取其中50 个点作为测试集，剩余150 个点作为训练集。采样点分布如图5 所示。

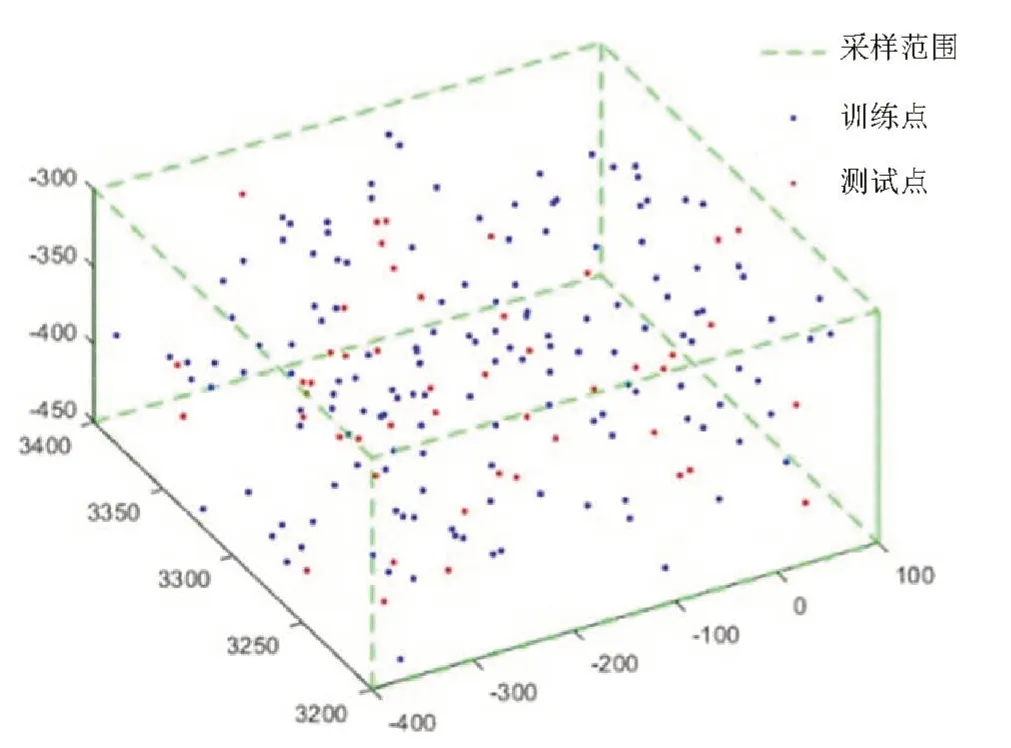
图5 采样点分布

X、Y、Z 三个方向的PSO 优化结果如图6 所示。

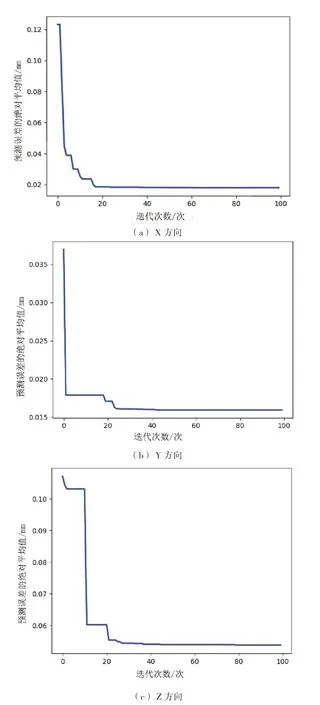
图6 三个方向上PSO 算法的迭代效果

从图6 中可以看出，随着迭代次数的增加，SVR 的预测值和真实值之差的绝对平均值，即预测误差绝对平均值逐渐减小，并最终逐步收敛到一个较低的值，这也意味着PSO 算法的适应度函数值逐渐增大且收敛。由PSO 算法优化三个SVR 模型的参数如表1 所示。

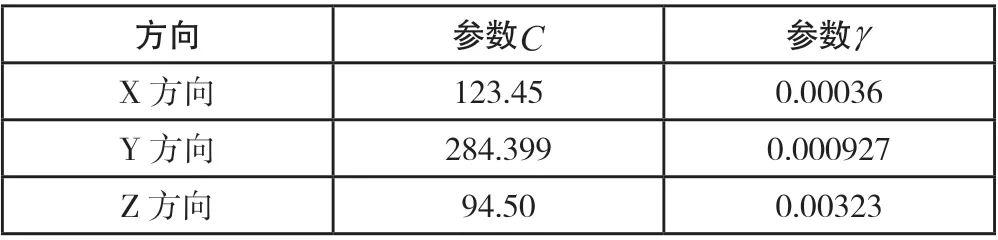
表1 PSO 优化的SVR 参数结果

图7 为X、Y、Z 三个方向SVR 模型预测补偿量与真实补偿量的对比，其中的SVR 模型采用表1 的参数数据。

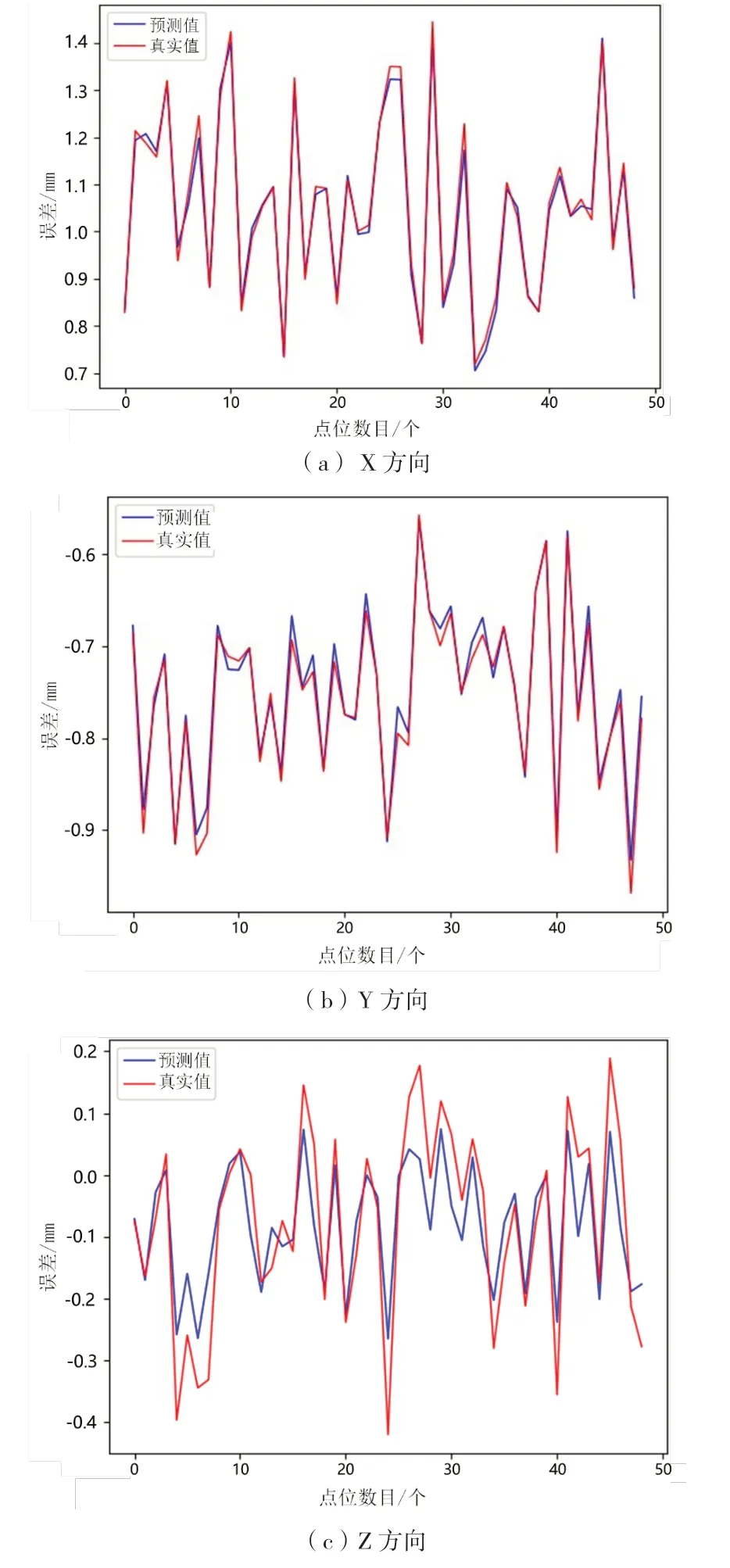
图7 预测补偿量与真实补偿量

SVR 模型在X、Y、Z 三个方向上的预测补偿量与真实补偿量之差的绝对平均值分别为：0.0159mm、0.018mm和0.0538mm。考虑到工业机器人重复定位精度大致在0.01mm 这一量级，可以认为SVR 模型在补偿量上的预测是准确的。同时，注意到SVR 模型在Z 方向上的预测误差明显高于X 方向和Y 方向。这是由于机器人自重对补偿量的影响会因为定位位姿的变化而变化，相当于引入了新的非线性因素，进而使SVR 模型预测效果在这一方向上变差。对于X 方向和Y 方向，因为不存在重力这一干扰，所以SVR 模型具有相对于Z 方向上更佳的预测精度。

3.3 精度补偿实验

本实验中，利用测试集的50 个点位进行离线编程，生成指令轨迹程序，并驱动机器人执行。之后直接利用SVR 模型计算出的预测补偿量驱动机器人进行补偿。此外，在PSO-SVR 模型训练的过程中，验证模型结果的测试集时还需要记录下这50 个点位在进行迭代闭环补偿前、后的误差，作为判断补偿效果的依据。误差补偿效果如图8 所示。

图8 误差补偿效果

在迭代闭环补偿前，机器人的平均定位误差为0.9024mm；在迭代闭环补偿后，机器人的平均定位误差降低至0.03mm；利用SVR 计算预测补偿量进行的补偿，机器人平均定位误差为0.0845mm。上述三种情况的定位误差方差分别为：0.014812、0.000091022 和0.0010119。

从数据上看，基于SVR 模型的补偿精度相对于机器人本身的定位精度，提高了一个数量级，且定位稳定性更佳。但相对于迭代闭环补偿，基于SVR 模型的补偿无论是从精度，还是从稳定性上来看，仍然存在一定的差距。这一差距是由SVR 模型本身的局限性所导致的，这种局限性包括模型容忍域引入的模糊性，核函数无法完美地将非线性样本修正为高维的线性样本，等等。尽管迭代闭环补偿本身的补偿过程就决定了其误差在0.05mm以内，但这种补偿过程极其费时，且在整个过程中都依赖于外部的测量设备（在本研究中即激光跟踪仪）。因此从补偿过程的快速性和便捷性来看，基于SVR 模型的补偿相对于迭代闭环补偿具有较大的优势。

4 结论

本文介绍了一种基于PSO-SVR 方法的工业机器人误差补偿方法。该方法首先通过对机器人进行闭环迭代补偿，获取机器人理论点位和真实补偿量所构成的训练集；再对该训练集进行训练，建立了SVR 模型，用于表征理论位置与补偿量之间的映射关系；在训练过程中，采用PSO优化算法整定了SVR 模型所涉及的惩罚参数以及核函数系数，以期通过SVR 模型计算达到更好的预测效果。

本研究搭建了以KUKA KR6 R700 sixx 为执行机构的实验平台，在其上依据PSO-SVR 方法训练了SVR 模型，并采用模型所预测的补偿量对测试集进行了补偿实验。实验结果表明，该方法能较准确地预测出工业机器人的误差补偿量，依据此补偿量进行的补偿能够有效地提升机器人的定位精度。此外，该方法的补偿过程相对于闭环迭代补偿更为快捷，为实际应用中工业机器人的误差补偿提供了解决途径。