比较生疑引好奇 问题提出探本源——对一道数学病题的探究教学及思考

花 奎

(南京师范大学第二附属高级中学,江苏 仪征 211900)

在使用高三数学模拟卷或复习用书进行教学时,由于命题者的疏忽,会出现一些条件信息错误或矛盾的例题或习题,此类题目称之为病题.大多数教师发现病题后,直接删除或改为正确题目,再让学生去训练或对其进行讲解.其实,病题是一种不可多得的教学资源.引导学生深层次地探究病因和修正错误,对数学概念的理解、数学思想的掌握、数学核心素养的提升具有不可替代的作用,同时有利于唤醒学生的好奇心,激发学生的探究欲望,培养学生的批判性思维,特别是有利于培养学生的问题意识及提出问题的能力.下面就谈谈一道病题的探究教学和点滴思考.

1 病题呈现及课前研讨

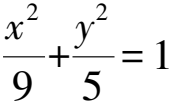
此题是2022年江苏教育出版社《高考总复习南方凤凰台一轮复习导学案(数学)》(学生用书)第146页中的一道题.

教师用书参考答案(记为解法1)如图1,根据椭圆方程可知a=3,c=2.设PF1=m,PF2=n,依题意有

图1

可得

(m+n)2-2mn=16,

从而

mn=10,

于是

不难发现编题者意图:让学生掌握椭圆定义的应用及整体处理的意识.笔者在备课时,发现由于编题者的失误,即题中点P是不存在的,例1是一个病题.对于这道题如何进行教学处理呢?笔者和其他教师进行了简单交流,主要有两种处理意见:

意见1(多数教师)在做题时没发现错误.既然是病题,那么就直接删除或换一道类似题目,也可以修改一下数据,就不要浪费学生时间了.高三教学任务重,抓紧时间多完成几道例题,应对高考.

意见2(少数教师)此病题中的错误不易发现,可以让学生尝试去做,去发现错误,探究错因,揭示问题的本质,有利于培养学生思维的批判性和深刻性.

爱因斯坦说过,发现问题比解决问题更重要.笔者比较倾向意见2,主张让学生先做,了解学生会怎样做,看学生能否发现错误,然后根据学生的情况,设计课堂教学.笔者整理了学生课堂解答情况,主要有以下4种解法.

解法1(同参考答案的方法(略),全班共52名学生,有32名学生使用了解法1.)

m2+(6-m)2=16.

即

m2-6m+10=0.

因为Δ<0,所以m无解.

(6名学生使用此法.其中有3名学生先用此法,后又划掉使用解法1;1名学生改用解法3;1名学生写到了Δ<0未敢下结论,只有1名学生下了无解的结论.)

解法3设P(x0,y0),由PF1⊥PF2,得

从而

即

故

(8名学生使用此法.)

(4名学生使用此法.)

根据学生的解答情况,只有2名学生认为这道题目有问题,就不去做了,也没有探究错误的原因.利用解法2的大多数学生认为自己的解法不对,但不认为题目有错,即使隐约感觉题目错了,也不敢质疑.用解法1、解法3及解法4求解的学生,顺风顺水,完全没有发现问题.

不难发现,学生普遍满足于完成作业(做习题),问题意识淡薄,即使有少数学生发现了问题,也没有进一步探究,缺少刨根问底的精神,同时也说明了学生在数学学习中好奇心已然丢失.鉴于此,笔者设计了“比较生疑,探寻病因—修正改进,探索规律—尝试学问,省悟本原”的探究教学流程,意在让学生学习数学知识和方法的同时,唤醒学生的好奇心,激活问题意识,培养学生提出问题的能力,激发学生的探究精神,揭示问题的本质.

2 教学过程

2.1 比较生疑,探寻病因

师(先展示解法1、解法3):同学们,通过这两种解法的学习,我们有什么感悟呢?

生1:点P在椭圆上,可以用椭圆的定义和椭圆的方程两种方式刻画.

师(展示解法2):这个解法又是怎么回事呢?

(学生看到解法2,略显诧异!)

生(多数):应该是计算错了吧!

师:真的算错了吗?大家再算算.

等了一会儿,学生开始叽叽喳喳地讨论起来.不少学生显露出困惑和好奇!

师:你们现在再比较这几种解法,思考为什么会产生截然不同的结果呢?哪个结果正确?为什么?

(此时学生的好奇心已被唤醒,顿时有了兴趣,开始了积极的讨论.)

师:说得很好!

师:难道题目真的错了吗?错在哪里呢?解法4又如何解释呢?

(教师故作惊讶!并在此时展示解法4,教室开始热闹起来.)

生4(过了一会儿):老师!这道题的图画不出来,是一道病题.

师(故作惊讶):噢!

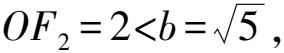
图2

师:太好了,解析几何内容的本质依然是几何!既然是几何,那一定离不开图形.生4抓住了点P需满足“PF1⊥PF2”的几何实质是一个圆,而它与椭圆无交点,说明题目中的条件是矛盾的.

2.2 修正改进,探索规律

师:没想到还真是题目有错误呀!编题者也不容易,我们能不能帮助其修正一下?

生5:可以将条件“PF1⊥PF2”改为“∠F1PF2=60°”.

师:大家对生5的修正做何评价呢?

生6:∠F1PF2=60°不一定可以.因为点P在椭圆上运动时,∠F1PF2是在变化的,它应该有范围!60°不一定在范围内.

师:生6提出的问题太好了!那么∠F1PF2的范围是什么呢?

生6:由图形可知,当点P在长轴的端点时,∠F1PF2取得最小值0;当点P在短轴的端点时,∠F1PF2取得最大值.

师:生6从图形直观感知当点P为短轴的端点时,∠F1PF2最大!这种猜想对吗?伽利略认为,仅靠自身的感受或者积累的经验来了解世界已经远远不够,必须求助数理式的理性.我们能给予理性证明吗?

(学生陷入沉思.)

师:要研究角的范围(或最值),一般是怎样去研究的呢?

生(众):要研究角的范围,通常可以先研究角的某一个三角函数的取值范围.

师:那么,选择哪个三角函数去研究方便呢?大家尝试一下.

通过学生独立思考、尝试、讨论,有以下想法:

想法1记∠PF2x=α,∠PF1x=β,设P(x0,y0),则

想法3在△F1PF2中,设PF1=m,PF2=n,则m+n=2a,由余弦定理得

又

从而

mn≤a2,

故

当且仅当PF1=PF2时取等号,即P为短轴端点时,∠F1PF2最大.

师:大家比较一下这3种想法,谈谈体会.

生(归纳整理):

想法1:在解析几何中,角的刻画通常用斜率和倾斜角,自然想到将∠F1PF2转化为2条直线的斜倾角之差,利用两角差的正切公式及斜率坐标公式来计算,最终转化为关于变量y0的函数来解决.方法朴素自然,也是解析几何中的一般方法.其不足为:计算量比较大,而且需要检验斜率不存在和∠F1PF2=90°的情况.另外,正切函数在[0,π)内不单调,很难说清何时角最大.

想法2:向量法也是处理夹角问题的常用方法.将∠F1PF2转化为向量夹角,利用向量夹角公式,进一步转化为坐标表示,最终转化为关于x0的函数来解决.其不足依然是计算量大.

想法3:抓住了△F1PF2的特点(焦点三角形),即由椭圆定义PF1+PF2=2a为常数,利用余弦定理并结合基本不等式迅速获得cos∠F1PF2的范围,再借助余弦函数的单调性,一气呵成!其不足为:若F1,F2不是焦点,即PF1+PF2不是常数,则不能顺利解决.

师:同学们总结得非常到位.今后在解决角的范围问题时,要根据条件,估计一下运算量,合理选择三角函数进行求解.

师:现在我们再思考可以将条件“PF1⊥PF2”改为“∠F1PF2=60°”吗?如果可以,那么如何解决?

生7:不难得到当点P在短轴端点P0时,

从而

∠F1P0F2>60°,

因此∠F1PF2可以等于60°.

设PF1=m,PF2=n,联立

得

(m+n)2-3mn=16,

从而

师:从几何角度看,将“PF1⊥PF2”改为“∠F1PF2=60°”,其本质是什么?

2.3 尝试学问,省悟本源

师:通过上述探究,同学们有哪些体会呢?

生:1)点P在椭圆上可以用椭圆的定义和方程两种方式刻画;2)点P在椭圆上运动时,当点P为短轴的端点时,∠F1PF2最大;3)角的范围的一般性求法;4)动点同时满足两个几何条件,其代数本质即为两个方程构成的方程组有解,几何本质就是两个轨迹有公共点.

师:同学们掌握得不错,特别是两个几何条件的代数和几何本质.现在,大家能否学做命题人,通过改变条件和结论,尝试编制一些试题?并说说编题的理由.

学生的积极性很高,大多数学生编制如下变式题并能说出解法.

(理由:椭圆确定,改变∠F1PF2的大小,只要保证∠F1PF2在规定的范围内,解焦点三角形就可以了.)

(理由:条件与结论互换,给出焦点三角形的面积,求∠F1PF2的大小.教师指出,△F1PF2的面积也有取值范围的要求.)

少数学生编制了开放题,让同学们大开眼界.

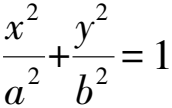
(理由:条件PF1⊥PF2表示点P在圆上,则椭圆与圆应有交点,因此对椭圆的离心率有要求.教师表扬并评价,让大家思考一下解法.)

(理由:受到变式2的启发,给出焦点三角形的面积,可以求∠F1PF2的大小,∠F1PF2的大小应在一定的范围内,从而可求出a的范围.)

(理由:高考试题中常出现结构不良的试题,我就尝试编出一个.3个条件都表示“隐圆”,关键是要研究哪一个圆与椭圆有公共点.)

学生在编题解题过程中学会提出问题的一些方法,理解了问题的本质,同时也体验了命题的快乐.教师在教学过程中对学生提出的问题应给予充分的肯定和鼓励.

3 点滴思考

3.1 创设问题情境,唤醒学生的好奇心

我国教育缺乏对学生创新能力的培养.创造教育存在问题的根本原因在哪里?张奠宙先生曾颇为沮丧地感慨道,中国公众和学生对考试以外的题目丧失了兴趣,缺乏好奇心,真是一种教育的悲哀[1].本案例的课前教学研讨中大多数教师认为:“既然是病题,就直接删除或者换一道类似题目,就不要浪费学生时间了,抓紧时间多完成几道例题,应对高考.”这些教师希望学生在高考中取得好分数,追求“多做题”,这无疑扼杀了学生的兴趣爱好,无端剥夺了学生的好奇心与思考力.何况,新高考数学凸显理性思维,导向独立思考、探究创新.周序教授认为,知识究竟带给学生一种怎样的感觉,并不在于知识本身是抽象还是具体,而是教师能否用一种调动学生兴趣、符合学生心理特点的方式进行教学,从而促使学生的发展[2].《普通高中数学课程标准(2017年版2020年修订)》(以下简称《课标》)明确提出,通过高中数学课程的学习,学生提高学习数学的兴趣,增强学好数学的自信心,养成良好的数学学习习惯,发展自主学习的能力;树立敢于质疑、善于思考、严谨求实的科学精神;不断提高实践能力,提升创新意识.本文首先创设符合学生认知的真情境(解法比较),通过解法1和解法3的学习与体会,先建构了一种“定义和方程”“数与形”的认知平衡,再展示解法2并提出“真的计算错误了吗?”“为什么会产生截然不同的结果呢?”等问题,让学生产生认知冲突,打破了之前的认知平衡,由奇生疑,唤醒了学生的好奇心,使学生产生了探究的欲望.

3.2 问题引导探究,揭示数学的本源

教学过程是一种提出问题、解决问题的持续不断的过程.问题是数学的心脏,让思维从问题开始,思维活动又形成新的问题,这种递进式的问题引领学生思考,也为学生的学习搭起了支架,指明着探究的方向,当然问题要针对学生思维的最近发展区提出,才能促进学生的发展[3].在本案例中,“难道题目真的错了吗?错在哪里呢?”这一问题激起了学生的探究欲望,为学生指明了探究方向.笛卡尔曾说,我所解决的每一个问题将成为一个范例,以用于解决其他问题.本文中“我们可以帮助修正一下吗?要研究角的范围(或最值),一般是怎样去研究的呢?”这一问题,不仅引领学生探索得到了“点P为短轴的端点时,∠F1PF2最大”的结论,更重要的是获得了解决“角的范围”问题的一般方法,这正是数学本质的一种追寻过程,自然地与学生内在需求产生共鸣.“你能尝试编制一些试题吗?”这一问题让学生在不断改变条件与结论的外在属性而提出新问题的过程中,更深刻地理解了“点P为短轴的端点时,∠F1PF2最大”和“动点P同时满足两个条件,代数本质为两个方程构成的方程组有解,几何本质就是两个轨迹有公共点”的数学本源.

3.3 课堂主体转向,培养问题提出的能力

教育的真正目的是让学生不断地提出问题、思考问题.《课标》明确提出,提高从数学角度发现和提出问题的能力、分析和解决问题的能力.《课标》在六大核心素养的具体阐述中,问题提出是数学抽象、逻辑推理、数学建模和直观想象这四大素养的表现之一.然而,课堂提问价值理性的缺失导致课堂提问及教学过程的异化.虽然我们的课堂上也有提问,但很少是由学生提出的,教师一直占据着课堂提问的主体地位,对学生成为课堂提问的主体形成了较大障碍,阻碍了新课程背景下课堂教学的提质增效.教师应当认识到课堂提问的作用在于激励学生发现自己的想法并提出问题,即课堂提问的价值理性是让学生作为课堂提问的主体提出问题并培养学生的问题意识[4].在本文中,教师提出的“编题者也不容易,我们可以帮助修正一下吗?”“大家对生5的修正有何评价呢?”等问题,就是基于课堂提问的价值理性,目的在于激励学生提出源于自己的好奇心、质疑及新发现的问题.李政道先生也曾说,学问,第一个字是“学”,第二个字是“问”,什么意思呢?就是你要学怎么样去问问题,这才是真正的学问.反思当前学校的学生做题、应考只能让学生学会作答别人的问题,而殊不知提出一个问题比解决一个问题更重要.让学生疲于做题的教育传统必须改变,教育改革需要将学生“外包”给了命题人的思想还回来,不妨给学生时间和空间,让学生学会自己提出问题.本文设计学生自己编题环节,在编题的过程中实现了提问的主体转向,培养了学生的学习兴趣、问题意识及创新思维,领悟了数学本质,特别是让学生逐渐学会了提出问题的方法,从而培养学生终身学习的能力.