一种LED紧凑匀光自由曲面透镜的设计方法

陈 成，杨永胜，郁新新，沈 达，牛绪儒

(连云港杰瑞电子有限公司，江苏 连云港 222000)

引言

发光二极管(Light Emitting Diode，LED)由于具有能耗低、光效高、体积小、寿命等优势，已在室内照明、汽车照明、道路照明、港口工业照明等各个照明领域得到了广泛的应用。然而LED光源自身的出光曲线遵循朗伯分布，光强度分布为中间强边缘弱，在此光分布场景下长期工作，将对人眼造成不适，因此需要对LED光源进行二次配光设计，使其产生均匀分布的照明光场。低功率的LED光源因其光源尺寸小，使得透镜中心高度与光源直径的比值大于5，可以将其作为点光源，采用成熟的能量映射法进行二次配光透镜设计[1]。随着市场经济和社会的发展，使得港口和厂房等工业场所要求更大照度的光场照明，从而要求光源具有更大功率和光通量，普通的LED点光源将无法满足需求，要求使用LED扩展光源。扩展光源的使用将导致透镜中心高度与光源直径的比值小于5，无法沿用点光源的配光设计方法。目前针对扩展光源的配光透镜设计方法主要有同步多曲面法[2]、广义函数法[3]和反馈优化算法[4-6]，其中同步多曲面法和广义函数法涉及复杂的数学转化且计算过程复杂，不利于设计不同规格扩展光源的配光透镜。反馈优化算法通过对比设计照度值和实际照度值，同时引入反馈修正参数实现均匀照明。

本文在基于极坐标系的点光源—目标光照度映射法基础上设计出针对LED点光源的自由曲面配光透镜，然后随机重叠多个点光源自由曲面透镜和采用粒子群反馈算法将重叠坐标作为优化变量进行扩展光源配光透镜的设计。与此同时，为了降低在优化过程中的人为干预，使用动态数据链接(Dynamic Data Exchange，DDE)技术，将数据处理软件Matlab和光学仿真软件Tracepro联合使用，Matlab负责算法处理以及坐标变化，Tracepro进行光学仿真和将光学结果传输给Matlab，整个流程具有操作性强和过程简洁的特性。

1 设计与优化方法

本文采用一种针对LED扩展光源的紧凑匀光自由曲面透镜的设计方法，主要由四部分构成：采用基于极坐标系的点光源—目标照度映射法，获取点光源入射到自由曲面的光线单位矢量和目标平面的坐标分布；根据透镜的边界条件，采用矢量形式的折射定律和递归计算方法获取透镜的自由曲面坐标分布；针对LED扩展光源，基于点光源的自由曲面透镜，采用叠加法获取扩展光源的自由曲面透镜，并使用基于粒子群算法的反馈优化方法对叠加方式进行优化，获取高光效和高均匀度的自由曲面透镜；最后使用DDE，将算法执行软件Matlab与光学仿真软件Tracepro进行联合，实现自由曲面透镜无人干预地计算优化仿真设计。

1.1 基于极坐标系的点光源—目标光照度映射法

为了适应目标平面各种形状光照度分布的要求，本文将在极坐标系ρ、γ下对目标平面进行网格划分，同时将在球坐标系θ、φ下，对点光源的光线辐射空间进行网格划分，获得点光源发出的光线与目标平面上的光照度分布映射关系，如图1所示。其中θ和φ分别为球坐标系中的俯仰角和方位角，ρ和γ分别为极坐标系中的极径和方位角。

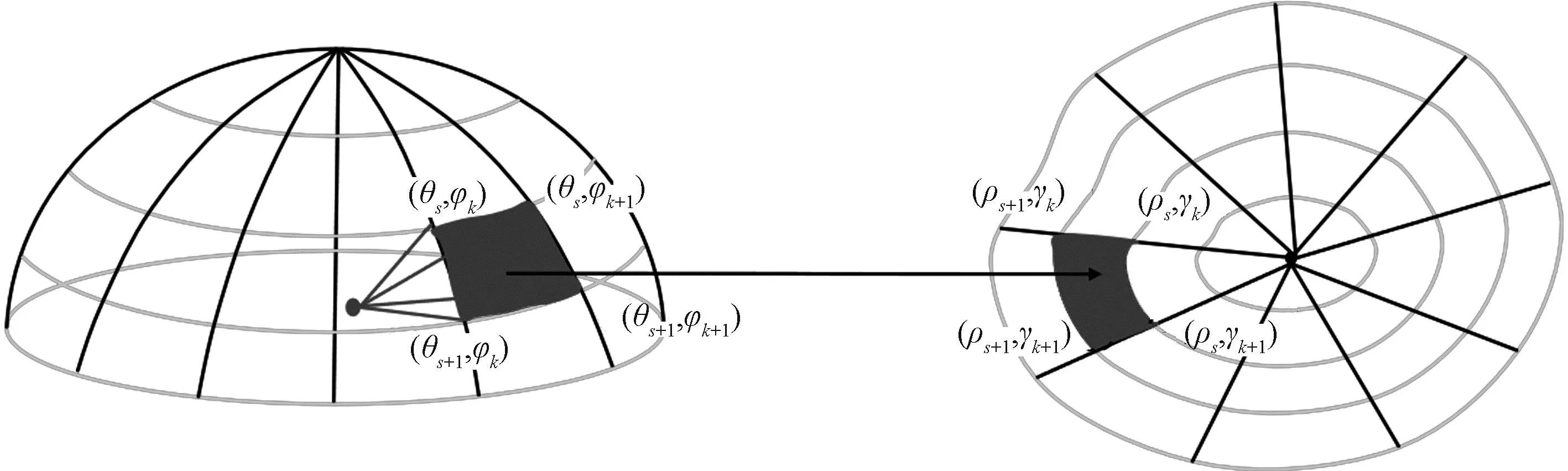
图1 网格划分与映射关系Fig.1 Grid division and mapping relationship

本文所用LED点光源呈完美朗伯体分布，光强分布与方位角φ无关，且光强分布满足余弦关系I(θ)=I0cos(q)，与此同时，假设目标平面上的照度分布为P(ρ，γ)。因此，对于无光学损耗的系统，由能量守恒关系可得点光源和目标平面之间的能量对应关系为[7]：

∬ΩSI(θ)sin(θ)dθdφ=∬ΩTP(ρ，γ)ρdρdγ

(1)

式中，ΩS表示点光源辐射光线的立体角；ΩT表示被照明的目标区域。

通过式(1)在光源与目标区域之间建立一系列的能量映射关系，分别获得光源不同立体角内的光线到不同目标区域传输方向的映射关系。

通过对式(1)左侧进行变量分离，实现点光源辐射空间的网格划分。将点光源辐射空间沿着俯仰θ和方位φ两个方向划分成M×N个网格，每个网格所包含的能量为E(i，j)(i=1，2，…，M；j=1，2，…，N)。沿着方位φ方向条状区域的所包含的能量使用式(2)计算：

(2)

式中，φmin和φmax分别表示点光源辐射的最小和最大方位角。对于LED点光源分别为0和2π，θmin和θmax为点光源辐射的最小和最大俯仰角，对于LED点光源分别为0和π/2。每个方位φ条状区域沿着俯仰θ方向划分的网格区域所包含的能量使用式(3)计算：

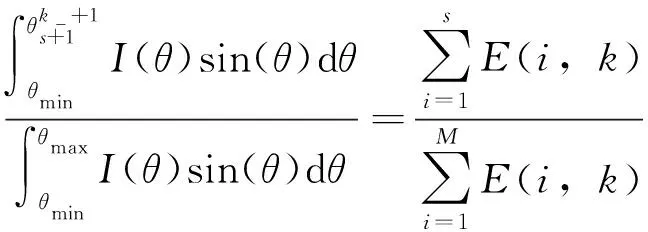
(3)

通过对式(1)右侧进行变量分离，实现目标平面区域的网格划分。将目标平面区域沿着极径ρ和方位γ两个方向划分成M×N个网格，且假设单连通目标域的边界为ρSC=f(γ)，为了保持与式(2)的能量分布相对应，沿着方位γ方向的扇形区域所包含的能量使用式(4)计算：

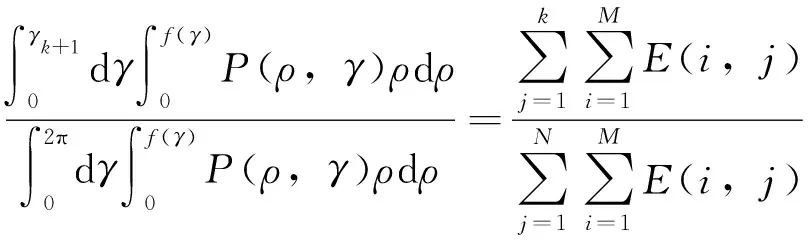
(4)

为了保持与式(3)的能量分布相对应，通过缩放边界ρSC，每个方位γ方向的扇形区域沿着极径ρ方向划分的网格区域所包含的能量使用式(5)计算：

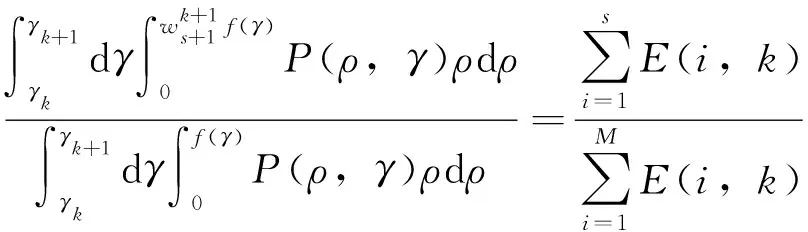
(5)

s=1，2，…，M+1；k=1，2，…，N+1

(6)

因此，通过式(2)～(6)可以实现点光源和目标区域的映射关系(θ，φ)-(x，y)。

1.2 构建点光源自由曲面透镜方法

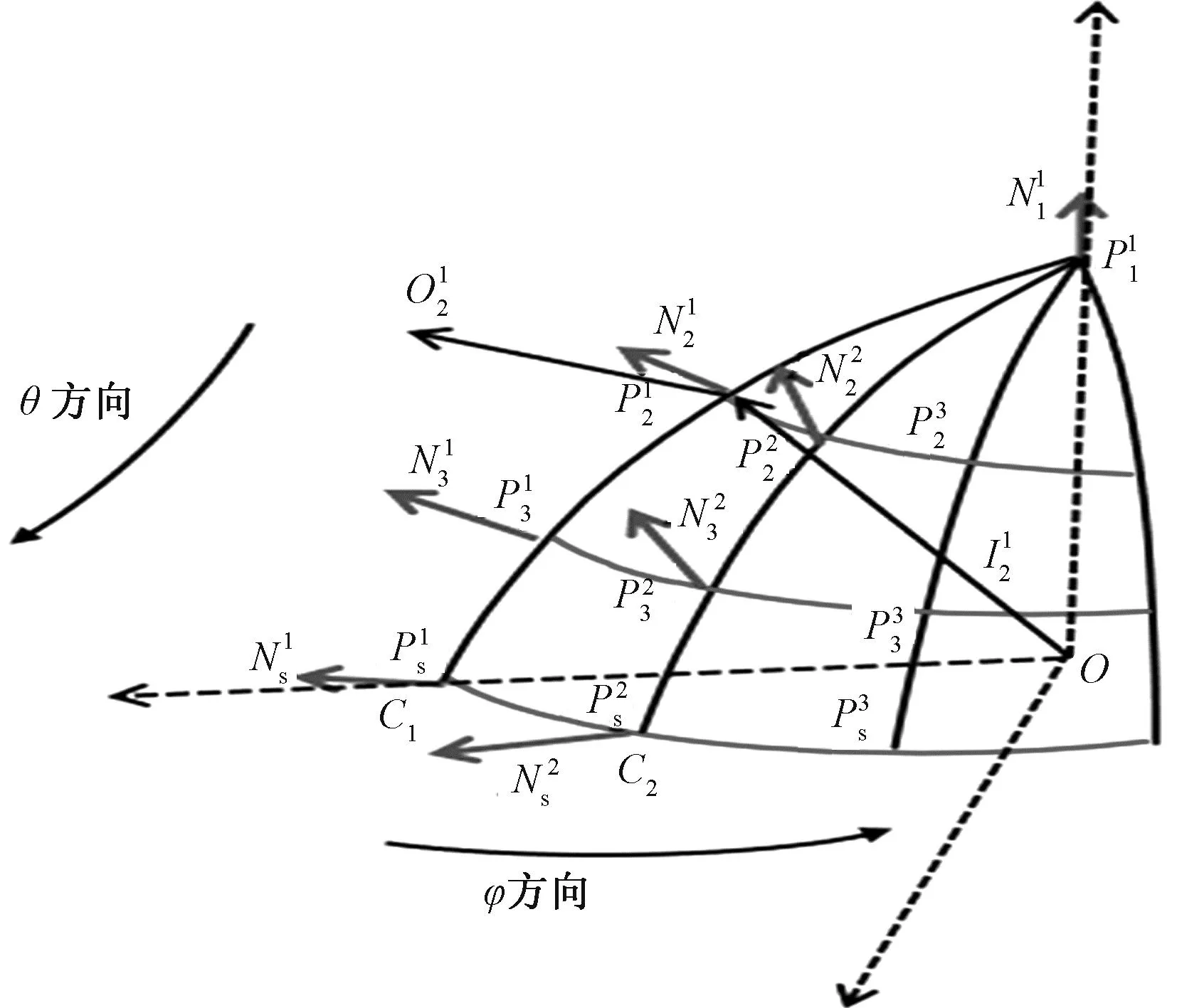
图2 点光源自由曲面透镜构建原理Fig.2 Construction principle of free-form lens with point light source

[1+n2-2n(O·I)]1/2·N=O-nI

(7)

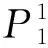
1.3 构建扩展光源自由曲面透镜

在设计中可将扩展光源看作一系列虚拟点光源的集合，采用叠加法，针对扩展光源的自由曲面透镜可由一系列点光源的自由曲面透镜叠加而来，具体构建过程如图3所示。对于每一个虚拟点光源，其对应的自由曲面透镜是相同的，图3中显示了将扩展光源分别看作由二个、三个和四个虚拟点光源对应的叠加自由曲面透镜的外轮廓，图3中虚线框表明自由曲面透镜的变化主要出现在透镜的中心区域[9]。通过以上分析，影响扩展光源自由曲面透镜出光效果的主要有虚拟点光源的数量和虚拟点光源分布的位置，因此可将上述两个因素作为优化变量。

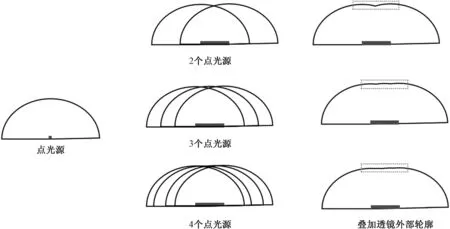
图3 基于叠加法的扩展光源自由曲面透镜构建原理Fig.3 Construction principle of extended light source free-form lens based on superposition method

先前的研究人员将扩展光源在x或y轴上均匀离散成几个虚拟点光源，然后构建扩展光源的自由曲面透镜，这种构建方式无法保证自由曲面透镜拥有最佳的出光效果。本文采用基于粒子群优化算法的反馈式叠加法来构建针对扩展光源的自由曲面透镜，将目标光场的均匀度U和照明系统的光效η作为粒子群优化算法的评价函数变量[10，11]，并且将在x或y轴上均匀离散的虚拟点光源的坐标作为初始优化变量，整个优化流程如图4所示。首先设置系统参数，包括光源尺寸、透镜中心高度、透镜材料、透镜到目标面距离以及目标光场形状等，然后基于1.1节的极坐标系的点光源—目标光照度映射法和1.2节的点光源自由曲面透镜构建法生成自由曲面透镜的采样曲面，使用粒子群优化算法产生虚拟点光源的坐标分布，利用叠加法生成扩展光源的自由曲面透镜，最后使用光学仿真软件获得目标光场的光均匀度U和光效η，满足评价函数要求时，获得扩展光源的自由曲面透镜。

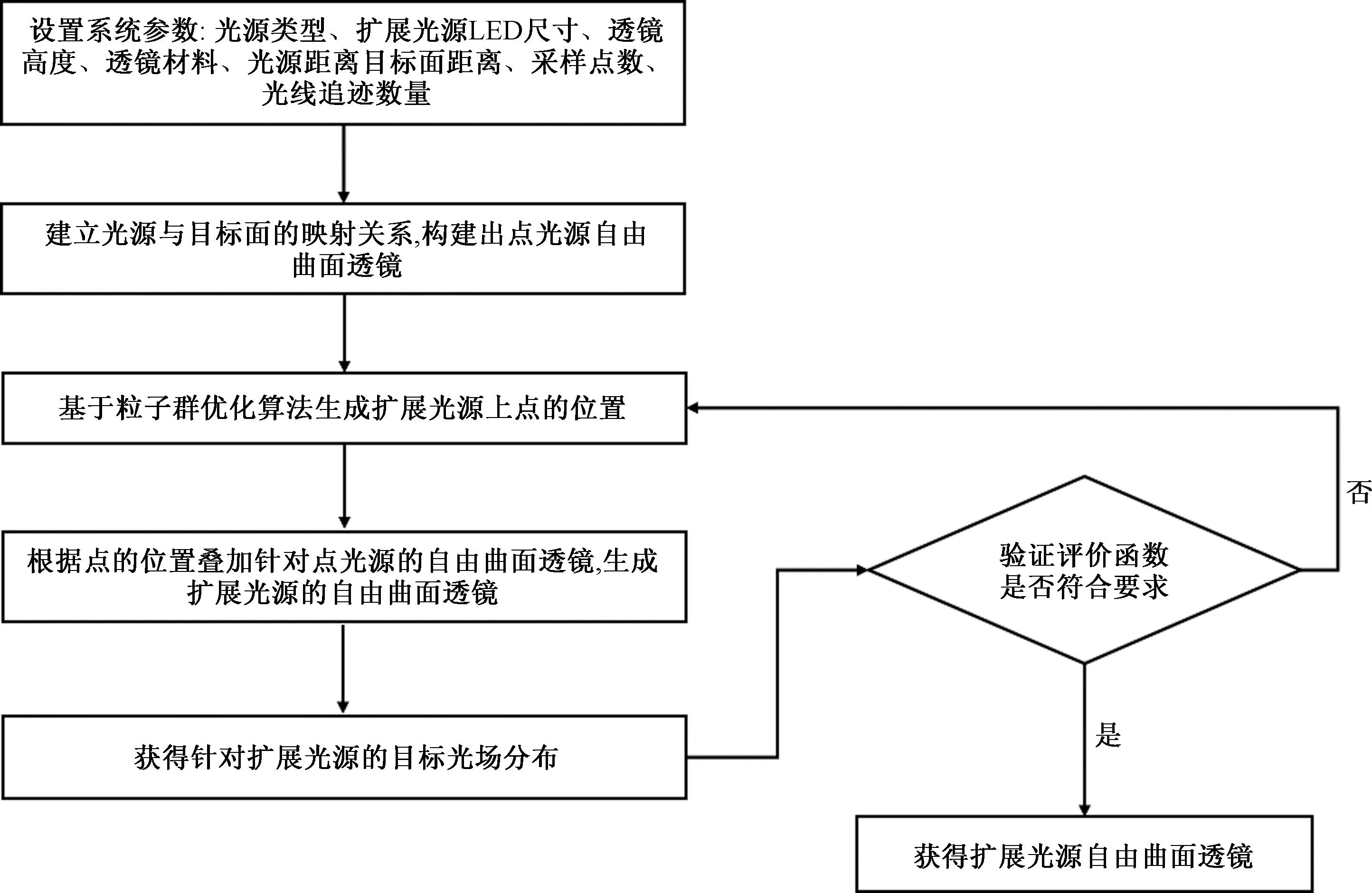
图4 基于粒子群优化算法的反馈式叠加法构建自由曲面透镜流程Fig.4 The free-form surface lens process was constructed based on the feedback superposition method of particle swarm optimization algorithm

1.4 多软件联用自动优化方法

DDE是一种可以建立服务器和客户端之间进行通信的技术，使用DDE技术可以实现数据计算软件Matalab和光学仿真软件Tracepro之间的联用[12]。两个软件通过ddeinit函数建立对话通道，使用ddepoke函数向Tracepro发送Matlab计算出的自由曲面采样曲线数据，然后使用ddeexec函数让Tracepro执行Scheme宏语言命令，构建自由曲面透镜和执行光学仿真，最后使用ddereq函数获取Tracepro所得的目标区域光场信息，Matlab软件根据获取的光场信息数据重新调整自由曲面透镜，直至获取目标光均匀度U和光效η的自由曲面透镜，交互过程如图5所示。

图5 Matlab与Tracepro通过DDE通信流程Fig.5 The free-form surface lens process was constructed based on the feedback superposition method of particle swarm optimization algorithm

2 仿真验证

为了阐明所提出的自由曲面透镜设计方法能有效改善扩展光源在目标区域光照度分布的均匀性和光效利用率，针对常规的圆形光场分布和矩形光场分布，设计了两款自由曲面透镜。具体的设计参数见表1。

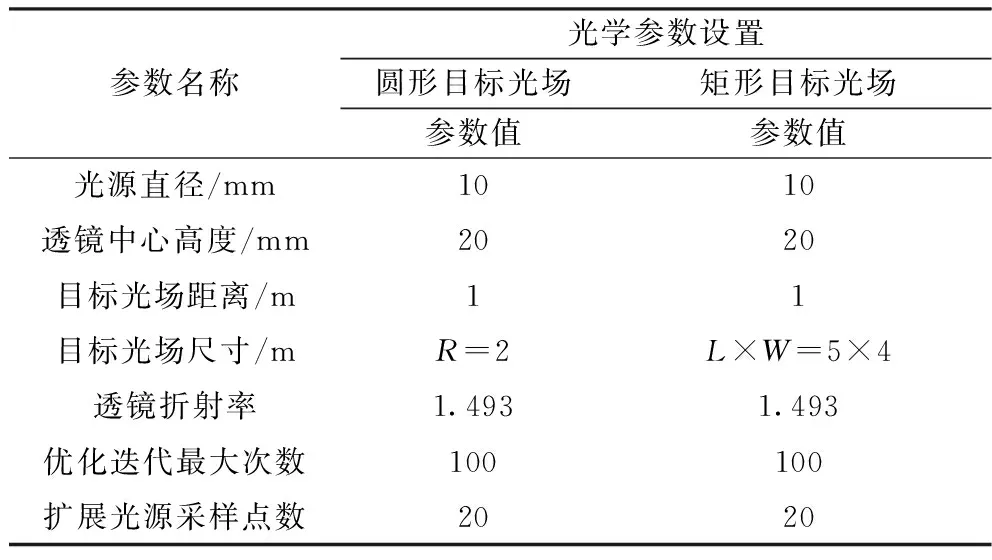
表1 基本光学参数设置

为了在目标区域获得均匀照度，要求光源划分的每个立体角单元具有相等的光通量，因此根据等式(2)和式(3)可以获得光源网格的划分，我们将方位角φ(π～π)均匀划分为N等份，将俯仰角θ划分成M等份，点光源对应的立体角网格划分如图6所示。

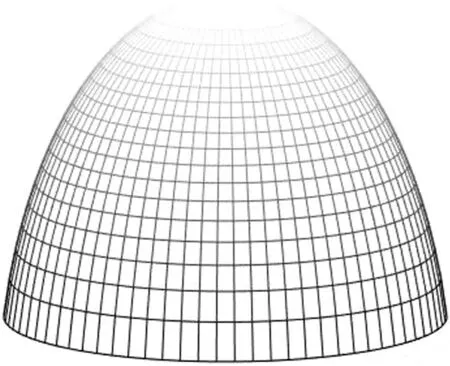
图6 点光源立体角网格划分Fig.6 Solid angle meshing of point light source

对于半径为R的圆形目标光场分布，其在极坐标下的边界函数为：

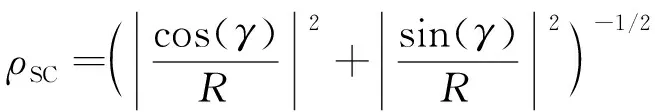
(8)

利用式(4)和式(5)可以获得与光源网格划分对应的目标区域网格划分，如图7所示，其中每个单元格的面积相同。

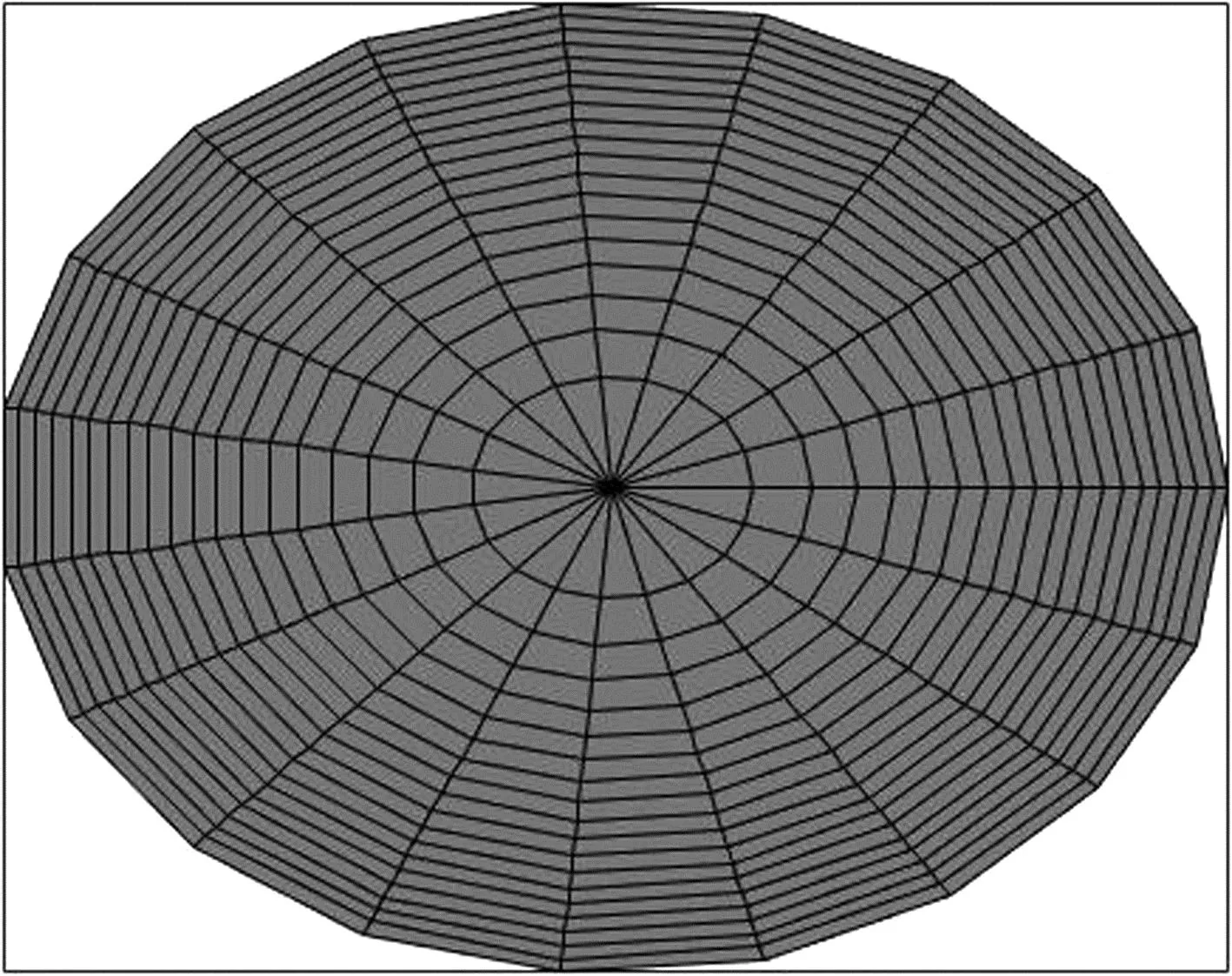
图7 圆形目标区域网格划分Fig.7 Circular target area meshing

对于长和宽分别为a和b的矩形目标光场分布，其在极坐标下的边界函数为

(9)

利用式(4)和式(5)可以获得与光源网格划分对应的目标区域网格划分，如图8所示，其中每个单元格的面积相同。

图8 矩形目标区域网格划分Fig.8 Rectangular target area meshing

当M=100，N=400时，对应于表1中的光学参数，使用1.2节方法和软件Matlab可以分别获得针对两个目标光场的点光源对应的自由曲面透镜的种子曲线和三维面型，经过计算，针对圆形目标光场的自由曲面透镜的种子曲线和三维轮廓如图9(a)和9(b)所示。

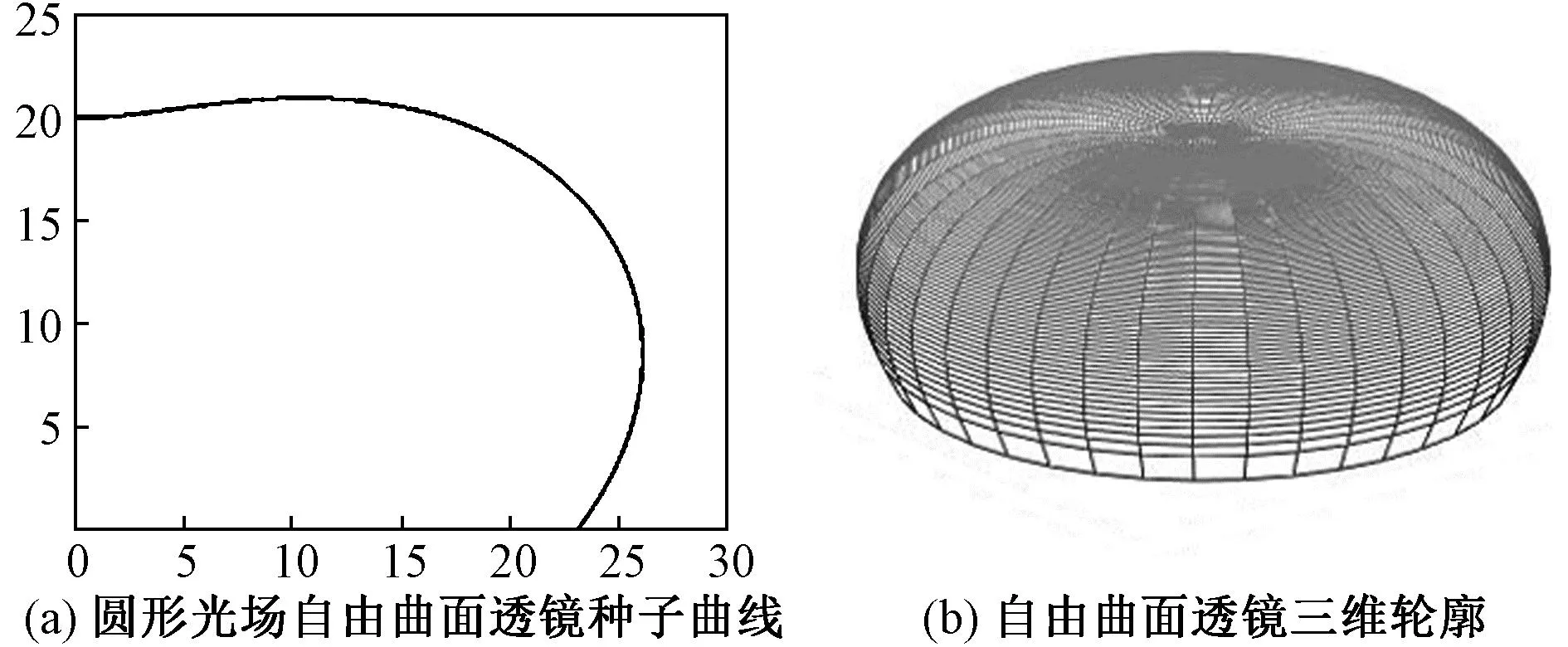
图9 圆形目标光场自由曲面透镜种子曲线和三维轮廓Fig.9 Circular target light field free-form lens seed curve and three-dimensional contour

与此同时，针对矩形目标光场的自由曲面透镜的种子曲线和三维轮廓如图10(a)和10(b)所示。

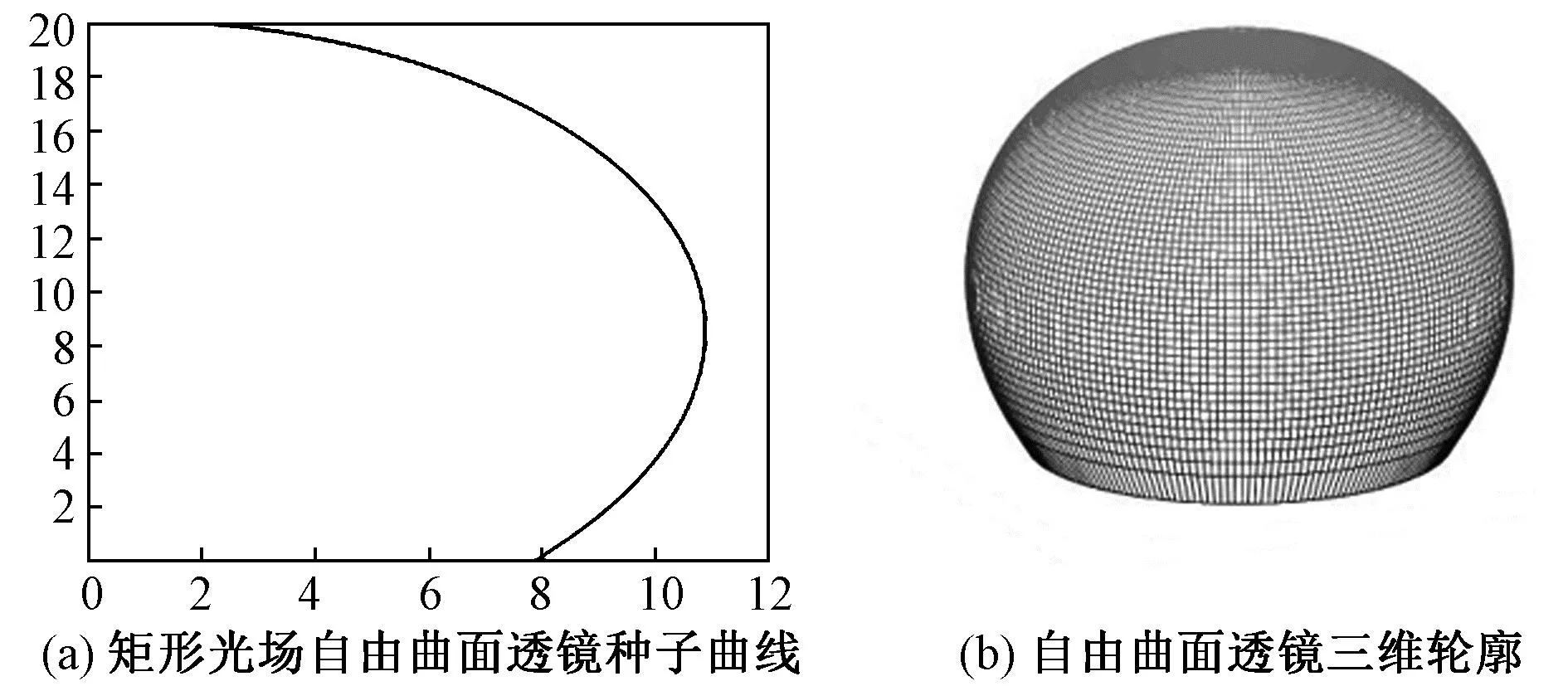
图10 矩形目标光场自由曲面透镜种子曲线和三维轮廓Fig.10 Rectangular target light field free-form lens seed curve and three-dimensional contour

利用DDE技术将Matlab计算所得的圆形目标光场自由曲面透镜和矩形目标光场自由曲面透镜的采样曲线数据传入Tracepro，然后使用Scheme宏语言在Tracepro构建自由曲面透镜，如图11(a)和11(b)所示。

图11 点光源自由曲面透镜Fig.11 Point light source free-form lens

使用1.3节提出的基于粒子群优化算法的反馈式叠加法构建针对扩展光源的自由曲面透镜，在粒子群优化算法中，将虚拟点光源的分布坐标作为优化变量，且将均匀分布的坐标作为初始变量值，将目标光场的光效η和光照度均匀性U作为评价函数f的影响因素，且附加临界条件，如式(10)所示。

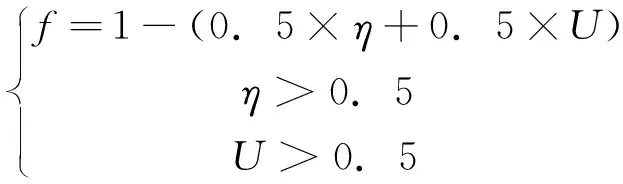
(10)

在Tracepro中根据虚拟点光源的坐标分布，对点光源的自由曲面透镜进行复制平移和几何逻辑运算，然后进行光学仿真获取目标区域的光效值和均匀度值返回Matlab软件中进行算法处理，经过不断优化的自由曲面透镜如图12所示。

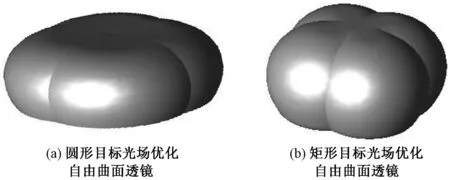
图12 扩展光源自由曲面透镜Fig.12 Extended light source free-form lens

为了说明经叠加优化算法获得的自由曲面透镜相比于点光源的自由曲面透镜，针对扩展光源在目标区域具有更高的光效和均匀性，使用Tracepro分别仿真计算了两者在目标区域的光照度分布，如图13所示。对于目标区域圆形光场分布，针对LED扩展光源，通过对比可得优化后的自由曲面透镜相比较于针对点光源设计的初始透镜，光效由0.79提升至0.90，均匀度由0.56提升至0.78。

图13 优化前后自由曲面透镜圆形目标光场光照度分布Fig.13 Optimize the illuminance distribution of circular target light field for front and rear free-form lens

如图14所示，对于目标区域矩形光场分布，针对LED扩展光源，优化后的自由曲面透镜相比较于针对点光源设计的初始透镜，通过对比可得光效由0.72提升至0.81，均匀度由0.68提升至0.84，中心的光场暗斑主要是由多个点光源自由曲面透镜叠加导致的面型起伏大造成的。

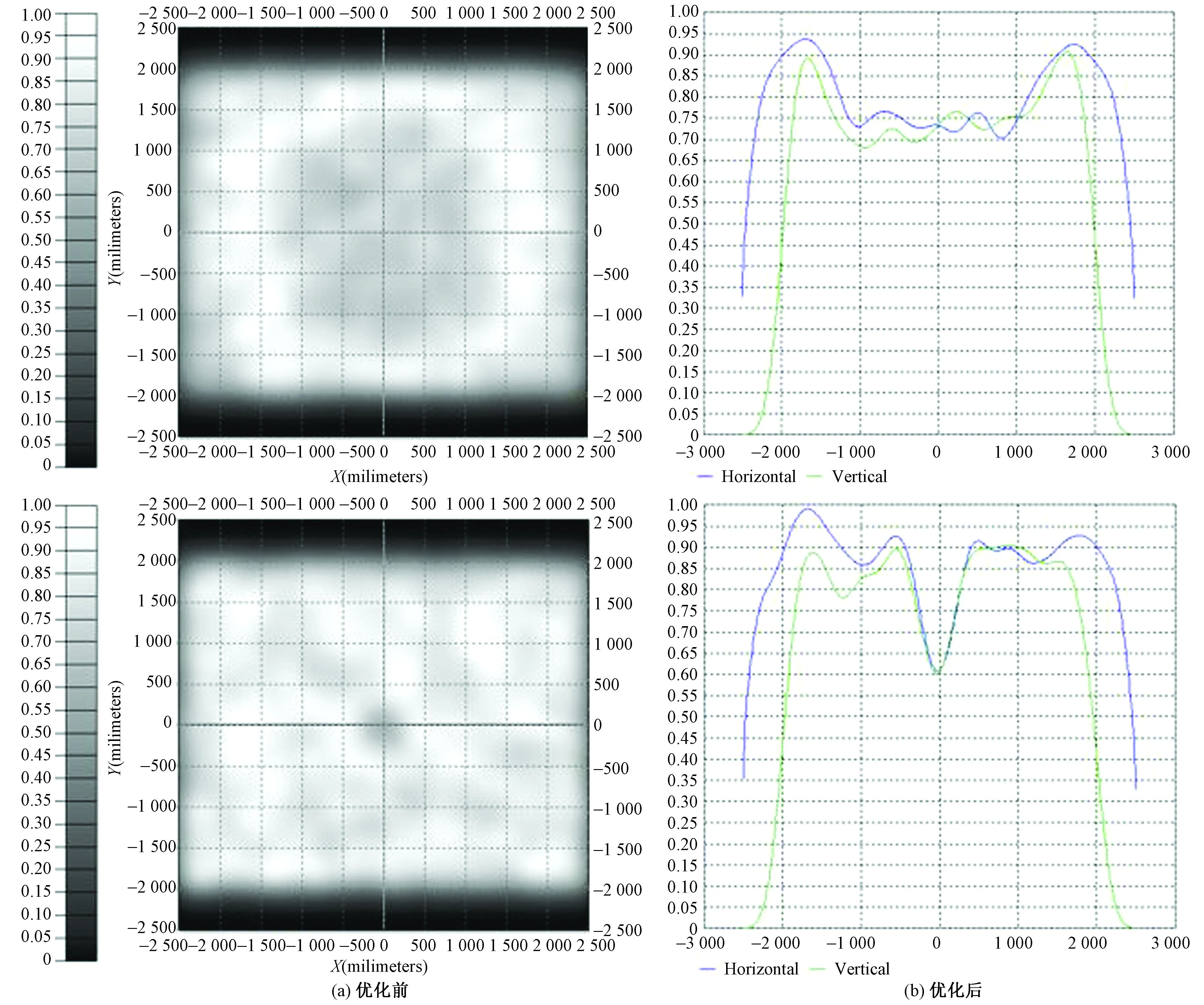
图14 优化前后自由曲面透镜矩形目标光场光照度分布Fig.14 Optimize the illuminance distribution of rectangular target light field for front and rear free-form lens

3 结论

本文研究提出了一种针对LED扩展光源设计紧凑匀光自由曲面透镜的方法，采用此方法设计的自由曲面透镜可以有效提高光效和光照均匀度。对于目标区域圆形光场分布，针对LED扩展光源，优化后的自由曲面透镜相比较于点光源设计的初始透镜，光效由0.79提升至0.90，均匀度由0.56提升至0.78。对于目标区域矩形光场分布，光效由0.72提升至0.81，均匀度由0.68提升至0.84。