基于改进NSGA-Ⅱ的考虑自动引导车充电策略的集成调度
2024-01-09薛海蓉韩晓龙
薛海蓉,韩晓龙
基于改进NSGA-Ⅱ的考虑自动引导车充电策略的集成调度
薛海蓉*,韩晓龙
(上海海事大学 物流科学与工程研究院,上海 201306)(∗通信作者电子邮箱xuehr1998@163.com)
针对自动引导车(AGV)在自动化集装箱码头(ACT)执行任务过程中的电量问题,提出基于改进的非支配排序遗传算法-Ⅱ(NSGA-Ⅱ)的考虑AGV充电策略的集成调度。首先,在岸桥、场桥和AGV集成调度模式下,考虑AGV在不同作业状态下的耗电量,并建立以最小化作业完工时间和总耗电量为目标的多目标混合规划模型;其次,为提高传统NSGA-Ⅱ的性能,设计自适应NSGA-Ⅱ,并将所提算法与CPLEX求解器、NSGA-Ⅱ和多目标粒子群优化(MOPSO)算法进行性能对比;最后,设计AGV不同充电策略并对设备数量配比进行实验研究。算法对比实验结果表明:相较于传统NSGA-Ⅱ算法,自适应NSGA-Ⅱ对双目标的优化分别提升了2.8%和2.63%。利用自适应NSGA-Ⅱ进行的充电策略和设备数量配比实验的结果表明:增加AGV充电次数能够减少AGV的充电时间,且调整设备数量配比至3∶3∶9和3∶7∶3时,场桥和AGV的时间利用率分别达到最高。可见,AGV充电策略及设备数量配比对码头多设备集成调度有一定影响。
自动化集装箱码头;自动引导车;充电策略;码头集成调度;自适应非支配排序遗传算法-Ⅱ;耗电量
0 引言
随着经济全球化进程不断推进,各经济体间的跨国贸易量迅猛增加。自动化集装箱码头(Automated Container Terminal, ACT)为提高自身竞争力,需要不断提高装卸效率。自动引导车(Automated Guided Vehicle, AGV)因绿色、安全和效率高等特点成为ACT常见的水平运输设备。与传统的水平运输设备相比,AGV作为一种蓄电池供电的设备,在运输过程中随时间变化不间断地消耗电量;因此,在进行多设备协调调度时,需要考虑AGV的充电过程以保证设备有足够的电量完成运输任务,避免在运输过程中出现AGV停车、拥堵码头等情况。
随着AGV在ACT的广泛使用,学者们加深了对AGV与其他水平设备集成调度的研究。Liu等[1]分析了卸载模式下AGV排队行为对岸桥和AGV集成调度的影响,指出岸桥数与AGV能耗成正比,与AGV平均排队时间成反比;范厚明等[2]基于AGV续航时间、双小车岸桥中转平台容量和堆场缓冲支架容量等约束条件,研究双小车岸桥与AGV联合调度下岸桥和AGV的最优配置;Zhao等[3]研究自动化岸桥(Automated Quay Crane, AQC)和AGV的协同调度,考虑AGV转运平台的容量限制,设计了两阶段禁忌算法进行求解;周玉清等[4]研究双循环策略下跨运车和岸桥的联合调度,考虑岸桥缓存区容量、安全时间等约束,设计了基于贪婪算法的响应性禁忌搜索算法,并对设备配比进行了实验分析。Yang等[5]研究岸桥、AGV和轨道式龙门起重机(Automated Rail-Mounted Gantry, ARMG)这3种运输工具的集成调度,提出基于防止路径拥堵的Bi-level遗传算法,能够有效地缓解AGV的路径拥堵问题并减少船舶在港装卸时间;Jonker等[6]研究装卸同步作业模式下岸桥、场桥和AGV综合调度问题,分别采用提出的改进模拟退火算法和分支定界算法进行求解,获得了更好的集成调度方案;Zhang等[7]提出AGV在双循环模式下与场桥、岸桥的联合调度,以最小化AGV等待时间为目标,设计带惩罚函数的混合粒子群算法进行求解,并证明了该调度模式的有效性;陈峥嵘[8]建立岸桥、AGV和自动堆垛机(Automatic Stacking Crane, ASC)的集成调度与AGV路径规划优化问题的双层规划模型,以降低作业产生的成本、减小能耗。
随着调度研究的不断深入,AGV在运输过程中的电量约束变得不可忽略,国内外学者开始研究AGV充电约束。吴洪明等[9]考虑AGV空重载的电量消耗差异和非线性充电的特点,确定在机会充电的模式下AGV的最佳机会充电区间;Sweda等[10]考虑充电次数和充电电量范围对电池寿命的影响,通过对比不同充电站设立规则,建立两阶段启发式算法求解问题;周小凡等[11]只考虑卸船作业,设置不同的AGV任务初始电量和充电结束条件,采用多频次充电的方式减少AGV在充电站排队等待充电的时间和任务完工时间;张亚琦等[12]在垂岸式堆场布局下,以AGV电池续航能力为约束考虑AGV充电过程对AGV实际作业的影响;赵涛等[13]在固定换电阈值情况下,综合考虑AGV换电站数和容量的限制,建立AGV的调度和充电的双层耦合模型;陈珲等[14]提出AGV的充电策略会极大程度影响设备完工时间;傅正堂等[15]在AGV电量非饱和状态下,优化装卸同步模式下的AGV作业调度;谢旦岚等[16]提出以离线充电为主在线充电为辅的充电策略,通过优化AGV数量配比提高AGV工作效率。
综上所述,现阶段较少深入研究多设备调度与AGV充电过程之间的关系,在考虑集成调度时忽略AGV需要充电的要求,或者在已知作业顺序的情况下研究AGV充电过程,少部分研究在实验时考虑了AGV空重载耗电不同和充电阈值等因素;因此在研究过程中通常忽略AGV充电过程,而无法进一步优化调度。因此,本文分析设备集成调度和AGV充电过程的内在关联,建立同时考虑AGV调度和充电的模型,研究AGV充电策略、设备数量配比对耗电量、设备利用率和设备完工时间的影响,并优化AGV充电策略。
本文以岸桥、场桥和AGV的集成调度为研究对象,在岸桥和场桥作业分配已知但作业顺序未知的情况下,考虑AGV的电量约束,首先,以最小化AGV最大完工时间和总耗电量为目标,建立考虑AGV充电过程的设备集成调度的多目标混合规划模型。其次,设计自适应非支配排序遗传算法-Ⅱ(Non-dominated Sorting Genetic Algorithm-Ⅱ, NSGA-Ⅱ),通过算例对比分析验证算法和模型的可行性。最后,通过算例数值分析,讨论AGV充电范围、AGV数、岸桥数对集成调度的影响。
1 问题描述
ACT的实际布局如图1所示。码头作业区域可以划分为岸桥作业区、AGV作业区和堆场作业区这3个部分:岸桥作业区进行岸桥的装卸载集装箱作业和AGV与岸桥的交接箱作业;AGV在AGV作业区进行集装箱的运输和充电作业;在堆场作业区场桥进行集装箱的堆垛作业和AGV与场桥的交接箱作业。
对于出口箱作业,场桥从堆场抓取出口箱后在交换区与AGV交接,AGV将出口箱运送至相应的岸桥位置并等待岸桥作业,直至岸桥抓取箱任务后AGV执行下一任务;对于进口箱作业,岸桥将进口箱从船舶放至AGV,AGV装载进口箱运输至交换区,等待场桥作业,直至场桥抓取箱任务AGV执行下一任务。
由于本文研究装卸同步的情况,因此需要考虑前后任务性质不同时设备的作业时间,避免出现各设备的作业时间冲突问题。以岸桥为例,若两个任务的作业性质相反,如先装后卸,需要往返于靠陆侧和靠海侧执行任务,因此需要计算两任务之间岸桥的移动时间;相似地,场桥在执行两个性质相同的任务时移动时间也需要计算。
2 模型建立
2.1 模型假设
1)不考虑AGV在码头运行过程中出现的路径冲突情况。
2)空重载不同情况下AGV行驶速度相同但耗电量不同,不考虑AGV等待时消耗的电量。
3)码头充电站数为1且不考虑AGV在充电站的排队行为。
2.2 符号定义和模型建立
集合和参数、变量说明如表1、2所示。
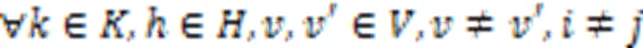
表1参数说明

Tab.1 Parameters description
表2变量说明

Tab.2 Variable description
目标函数式(1)(2)分别表示本文的两个目标函数——最小化AGV最大完工时间和最小化AGV总耗电量:
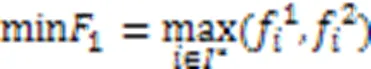
式(3)~(8)表示岸桥、场桥和AGV执行集装箱作业时,每个任务能且仅能被执行一次。特别地,当AGV执行完作业任务后执行充电任务,则充电任务为确定的任务。
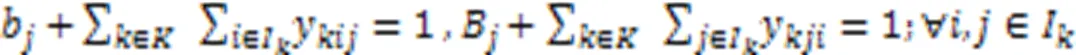
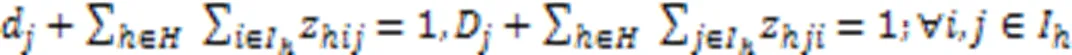
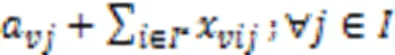
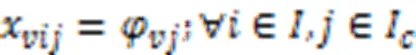
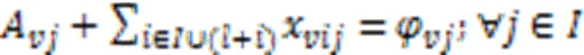
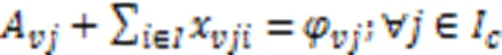
式(9)(10)表示AGV、岸桥和场桥有且仅有一个开始任务和结束任务。
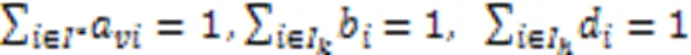
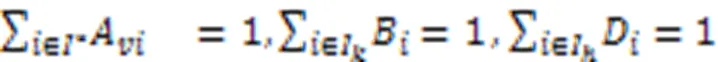
式(11)~(14)对岸桥、场桥和AGV的任务流进行约束。
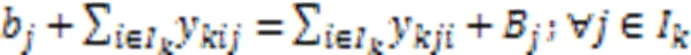
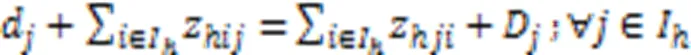
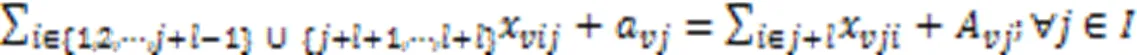
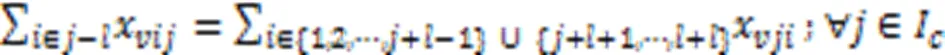
式(15)表示每个任务有且仅由一辆AGV执行,式(16)表示AGV不能连续执行两个充电任务。
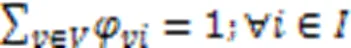
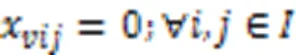
式(17)(18)表示岸桥或场桥开始执行任务的时刻不早于AGV到达设备指定位置的时刻;式(19)(20)表示对岸桥和场桥执行任务的起始时间进行约束。
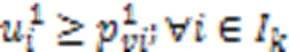
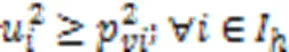
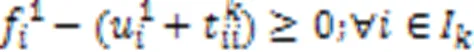
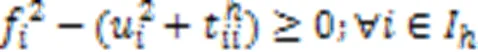
式(21)表示AGV执行装载任务时,到达岸桥时刻应不早于它离开场桥时刻与它在任务节点间运输集装箱时间之和;式(22)表示AGV执行卸载任务时,到达场桥时刻应不早于它离开岸桥时刻与它在任务节点间运输集装箱时间之和;式(23)(24)表示如果岸桥或场桥连续执行任务和,那么岸桥或场桥开始执行任务的时刻不早于岸桥或场桥结束执行任务的时刻加上设备在两任务执行位置之间的移动时间。
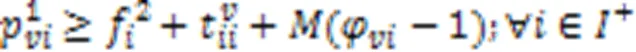
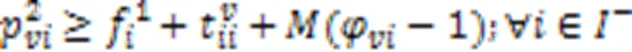
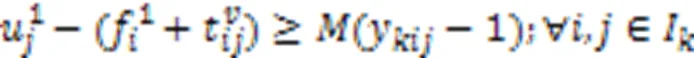
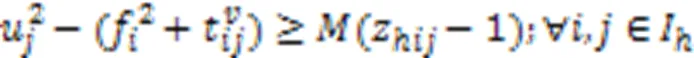
式(25)表示AGV在结束充电任务后执行作业任务且作业任务为进口箱任务时,AGV到达岸桥时刻与AGV到达充电站时刻之间的关系;反之,式(26)表示若后继作业任务为出口箱任务,AGV到达场桥时刻与AGV到达充电站时刻之间的关系。
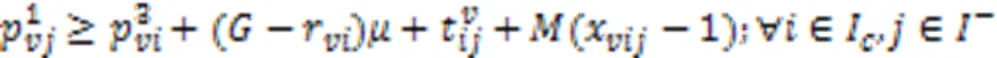
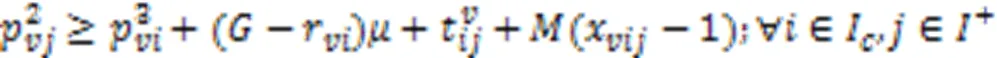
式(27)(28)表示由同一AGV执行的两个相邻作业任务之间开始工作时间约束。
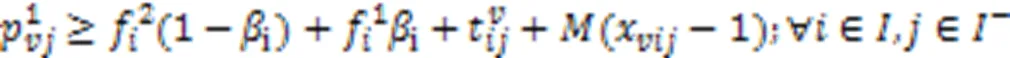
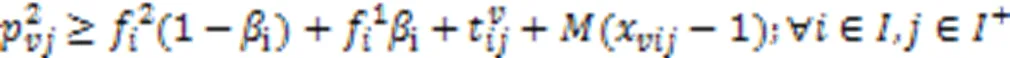
AGV电量约束 式(29)表示AGV完成作业任务时的剩余电量大于安全阈值,反之前往充电;式(30)~(31)表示两个任务之间的开始电量的约束。
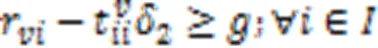
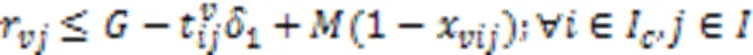
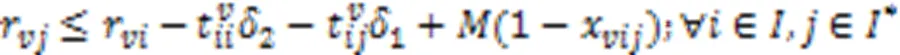
式(32)表示若AGV在完成任务后前往充电站充电,则到达充电站的时刻不早于AGV完成任务的时刻加上AGV移动至充电站的时间。
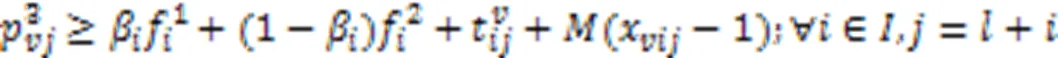
总耗电量约束 式(33)(34)表示两个相连任务之间的总耗电量约束。
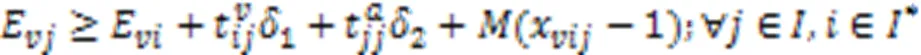

3 算法设计
NSGA-Ⅱ是由Deb等[17]提出用于求解多目标优化问题的算法。该算法是在传统遗传算法的基础上增加快速非支配排序、拥挤度计算等环节,对初始化种群进行非支配排序和遗传操作产生下一代种群,并采用精英保留策略,将父代和生成的子代混合后形成新种群进行计算,重复以上操作直至循环结束。但由于交叉概率和变异概率是固定的,可能会破坏优良个体或潜在优良个体,降低了下一代个体的质量,从而降低了算法结果质量。在操作过程中引入自适应函数,随着个体适应度值的变化,能够动态的调整算子大小,更大概率地保留优良个体。
3.1 染色体编码和解码
3.1.1编码
由于考虑作业的工作顺序和AGV车辆调度,每个个体设置4条染色体,染色体编码如图2所示。染色体的长度表示任务数。
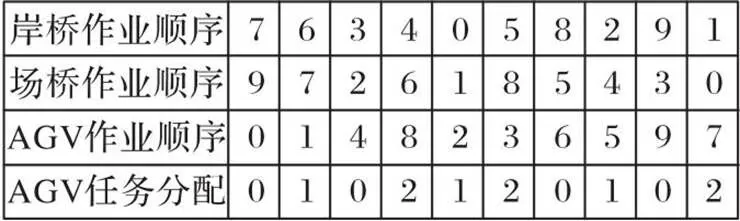
图2 染色体编码
3.1.2解码
假设现有装卸作业任务10个、2台岸桥、3辆AGV和2台场桥,岸桥和场桥的作业分配已知。初始化种群如图2所示,则岸桥和场桥的初始作业顺序如下:
岸桥①:7→4→0→8→9 岸桥②:6→3→5→2→1
场桥①:9→7→1→5→3 场桥②:2→6→8→4→0
如图2所示,第3行中的任务对应第4行中的,则表示任务由第台AGV执行,如第3行中任务8对应第4行中的2,则任务8由第2台AGV执行,且根据第4行得知任务8为第2台AGV的第一个任务,AGV的初始作业分配和顺序如下所示:
AGV0:0→4→6→9
AGV1:1→2→5
AGV2:8→3→7
3.2 染色体修复
遗传过程在解码之前,需要对染色体进行修复操作。一是因为在初始化染色体种群时,没有对各编码位置进行约束,可能存在非可行个体;二是在经过交叉、变异等遗传操作后,也可能产生非可行个体,因此对染色体进行修复是十分必要的。修复染色体的伪代码如算法1所示。
算法1 染色体修复流程。
输入 个体;
输出 修复后个体。
1) 对染色体进行解码并获得任务在每个设备上的工作序列agv,qc,yc
2) Forinagv:
3) Forinagv:
4) 获得任务和任务在岸桥、场桥和AGV的执行顺序0,1,2和0,1,2
5) 基于agv的工作调度,判断任务和任务在岸桥的工作顺序是否需要修复
6) If (1-1)(0-0)<0或(2-2)(0-0)<0:
7) 基于agv的工作序列修复qc,yc
8) 更新染色体
3.3 自适应交叉、变异概率
本文基于Srinivas等[18]提出的自适应遗传算法,对自适应函数进行改进使它能够优化多目标算法,自适应如式(35)(36)所示:
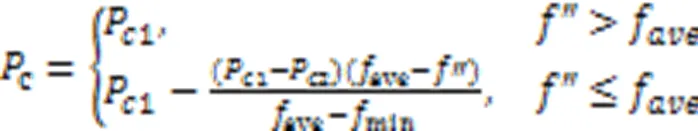
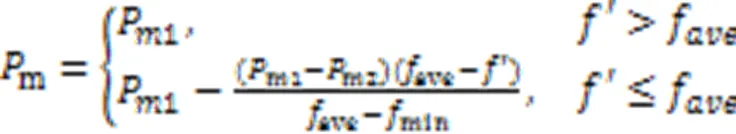
3.4 交叉操作
为了避免在对工作序列进行交叉操作后出现个别任务重复和缺失的情况,对表示工作序列的染色体采用顺序交叉的方式,对表示任务分配的染色体采用两点交叉的方式。
3.4.1顺序交叉
以岸桥作业顺序为例,根据自适应交叉概率选中两个染色体父代1、父代2,在两条染色体上随机生成不相邻的两个交叉点,以父代1为例,首先生成子代1,子代1被选中的基因的位置与父代1相同;其次,找到父代2中基因所在位置,再将其余基因按顺序放入子代1中,子代2同理可得,如图3所示。
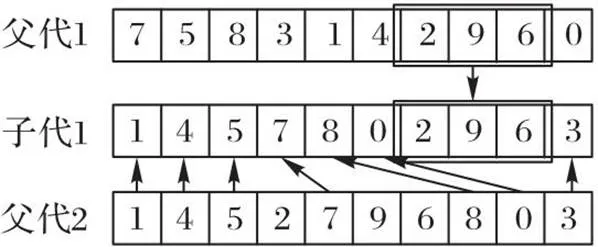
图3 染色体顺序交叉
3.4.2两点交叉
对于表达AGV作业分配的染色体,采用两点交叉方式。先得到随机生成的两个交叉点,再交叉父代1和父代2两点之间的基因片段生成子代1和子代2,其中子代1产生过程如图4所示。
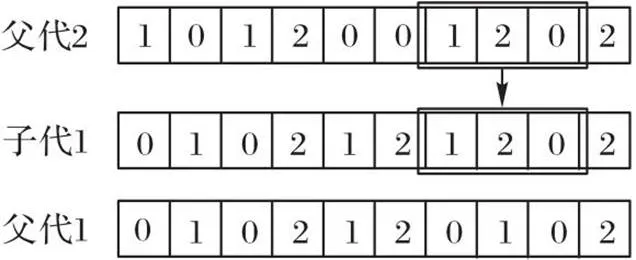
图4 染色体两点交叉
3.5 变异操作
变异操作与交叉操作相似,首先,根据自适应变异概率选中父代染色体;其次,随机生成两个变异点;最后交叉两个变异点位置对应的基因,如图5所示。
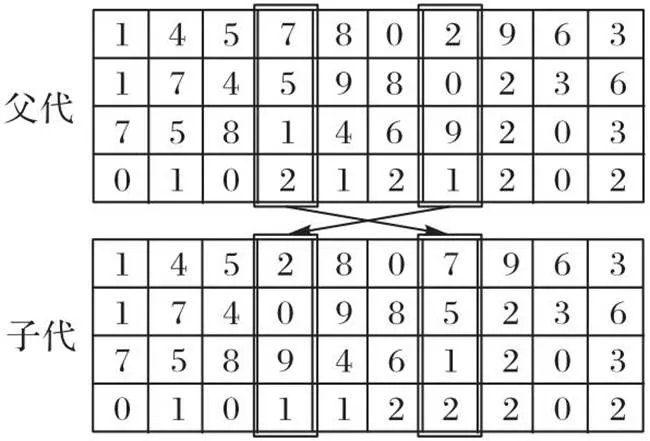
图5 染色体变异
3.6 算法流程
自适应NSGA-Ⅱ的具体流程如图6所示,其中表示当前种群迭代次数,表示最大迭代次数。
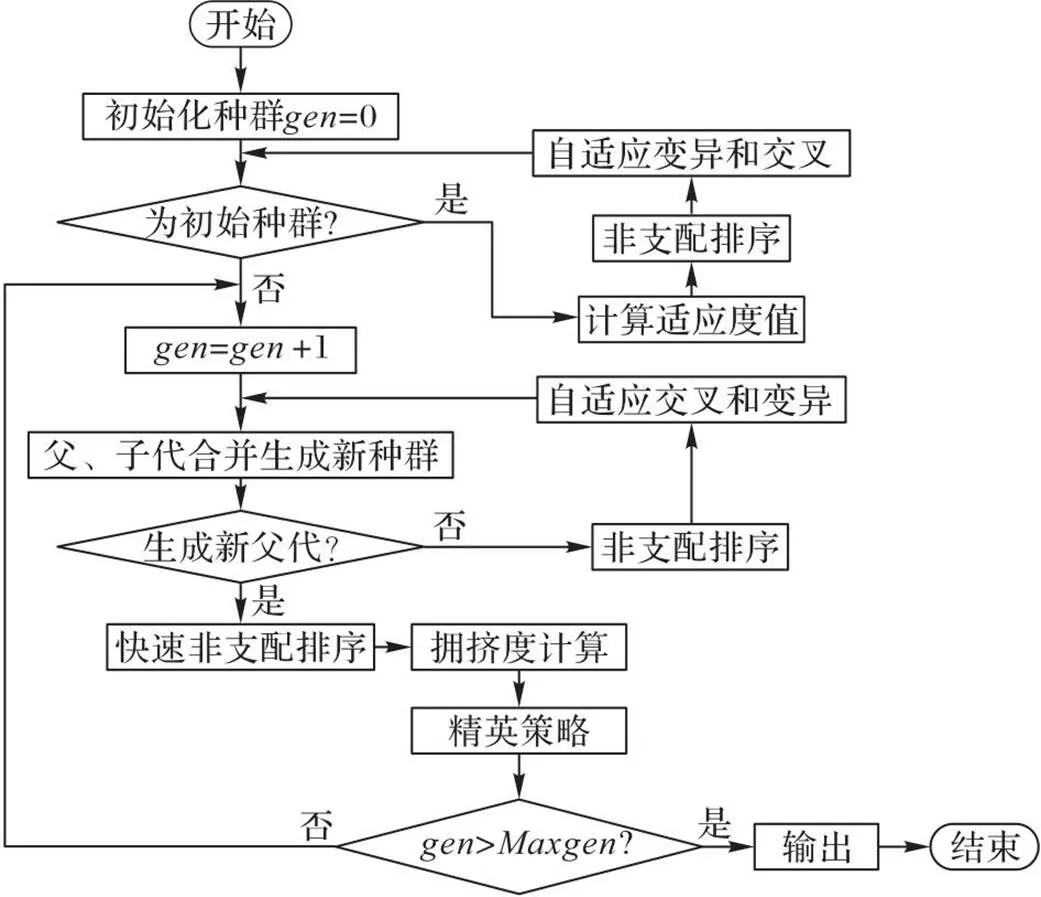
图6 自适应NSGA-Ⅱ的流程
4 算例分析
4.1 算例设计
本文以ACT实际布局为参考,对岸桥、场桥和充电站的位置进行适当修改,在Windows 64系统中使用Python 3.8检验模型和算法的可行性。
已知岸桥和场桥的作业分配、作业装卸性质采用均匀分布随机生成,且装卸比和设备任务比保持在1∶1。岸桥数为3,堆场数为5,充电站数为1,AGV的最大电池容量参考文献[19]中设为200 Ah。
本文设计以下3个实验:实验1对比CPLEX求解模型得出的精确解与NSGA-Ⅱ[17]、自适应NSGA-Ⅱ[18]、多目标粒子群优化(Multi-Objective Particle Swarm Optimization, MOPSO)算法[20]得出的近似解,验证模型的有效性;实验2利用自适应NSGA-Ⅱ,对不同充电策略下AGV最大完工时间、总耗电量和充电时间进行对比并分析不同参数下各充电策略的优劣;实验3研究场桥和AGV数量配比变化对设备时间利用率的影响。
4.2 性能分析
为使AGV在小规模实验中执行充电任务,在此实验中对参数进行适当调整,以验证模型的可行性,设备参数源于文献[21-22],表3为相关参数设置。
表3相关参数
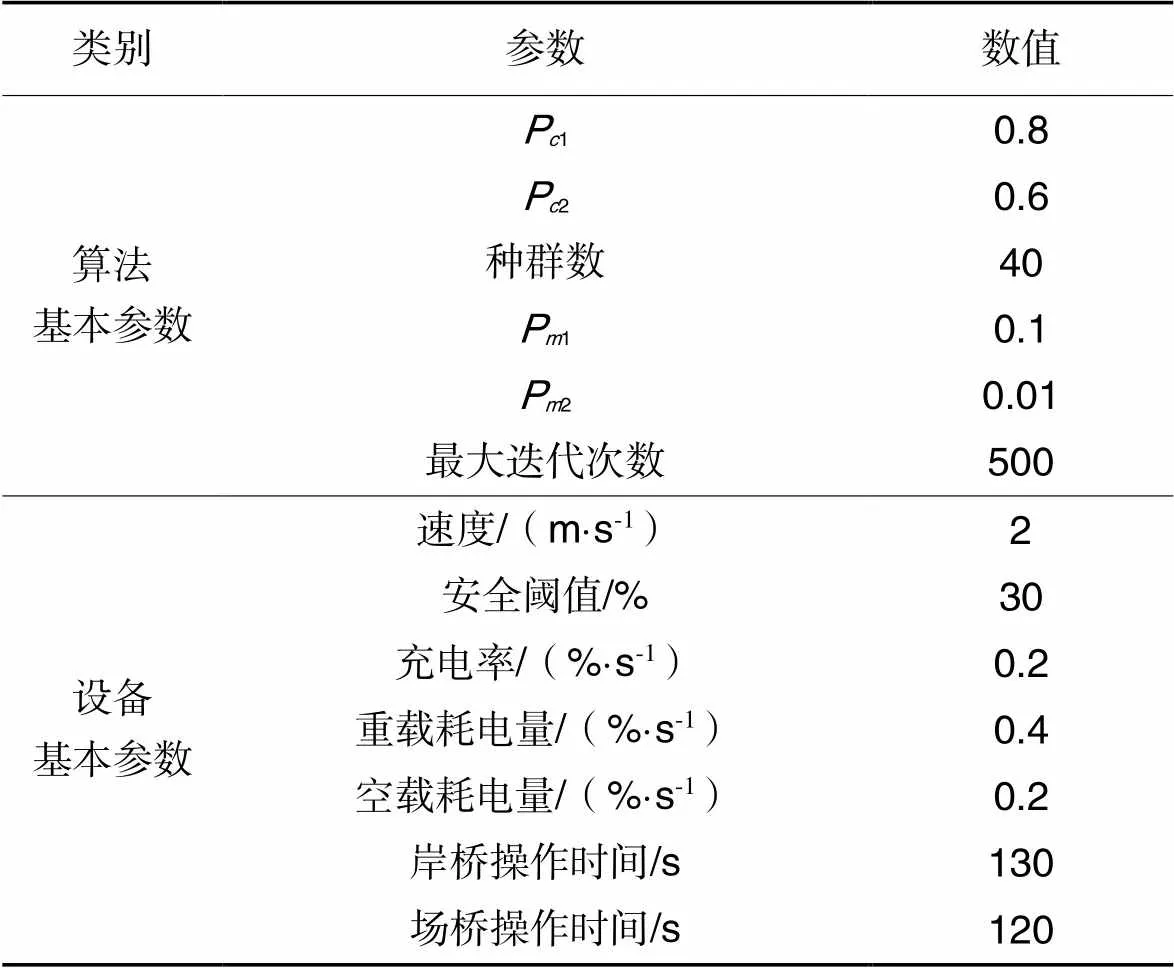
Tab.3 Related parameters
本文设置6组实验,任务数设置为10、15、20,AGV数设置3、4、6。由于CPLEX无法求解多目标问题,因此在利用CPLEX求解时以AGV最大完工时间为目标。表4为CPLEX、自适应NSGA-Ⅱ、NSGA-Ⅱ和MOPSO算法运行10次的平均求解结果,其中f1和f2分别表示最大完工时间和AGV耗电量的平均值,time表示4种求解方法的平均运行时间。表5为4种算法在目标值上的差距绝对值对比表,其中GAP1、GAP3和GAP5分别表示自适应NSGA-Ⅱ与CPLEX、NSGA-Ⅱ和MOPSO算法在f1目标值上的差距绝对值,GAP2、GAP4和GAP6分别表示它们在f2目标值上的差距绝对值。
表4算法求解目标值及运行时间结果
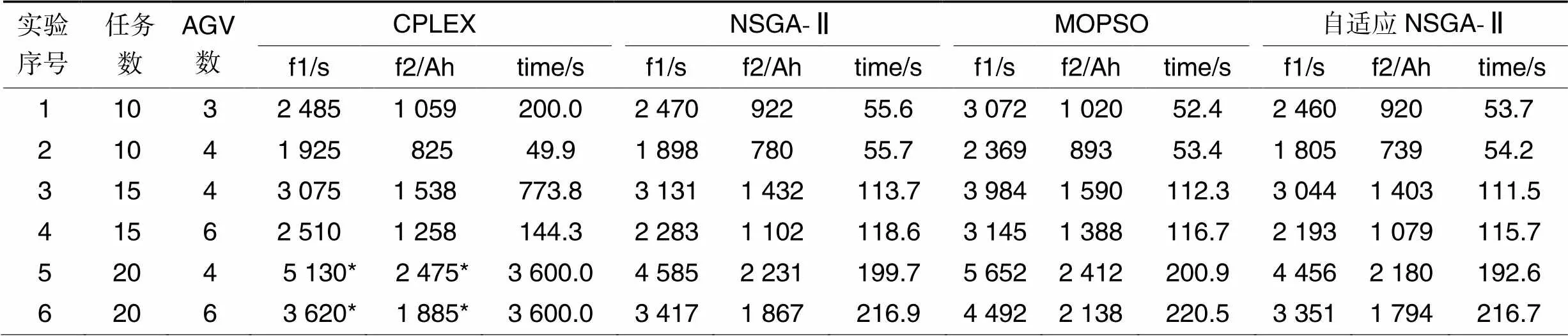
Tab.4 Objective solution results and running time of algorithms
注:*表示运行时间为3 600 s时CPLEX得出的一个可行解。
首先对运行时间和结果进行分析。如表4、5所示,当任务数较少时,自适应NSGA-Ⅱ的结果最优,CPLEX的求解结果较差于NSGA-Ⅱ的结果,当任务数增大时,NSGA-Ⅱ得出的f1和f2值逐渐低于CPLEX求解器得出的值,而自适应NSGA-Ⅱ仍然优于前二者,且自适应NSGA-Ⅱ与NSGA-Ⅱ之间的差距变大。当任务数从10增长到20时,MOPSO算法的实验结果始终最差。实验结果表明,自适应NSGA-Ⅱ求解得出的f1目标值分别优于NSGA-Ⅱ和MOPSO算法2.80%和24.03%;而自适应NSGA-Ⅱ对f2目标值相较于NSGA-Ⅱ和MOPSO算法提升较小,分别为2.63%和14.46%。从运行时间看,CPLEX的运算时间随任务数的增加呈倍数增长。当任务数从10增加到15时,CPLEX的运算时间增加了723.9 s,当任务数为20时,在3 600 s内CPLEX无法得出最优解;而自适应NSGA-Ⅱ运算时间随着任务数的增加变化幅度较小,且运算时间最少。
表5算法求解目标值差距对比
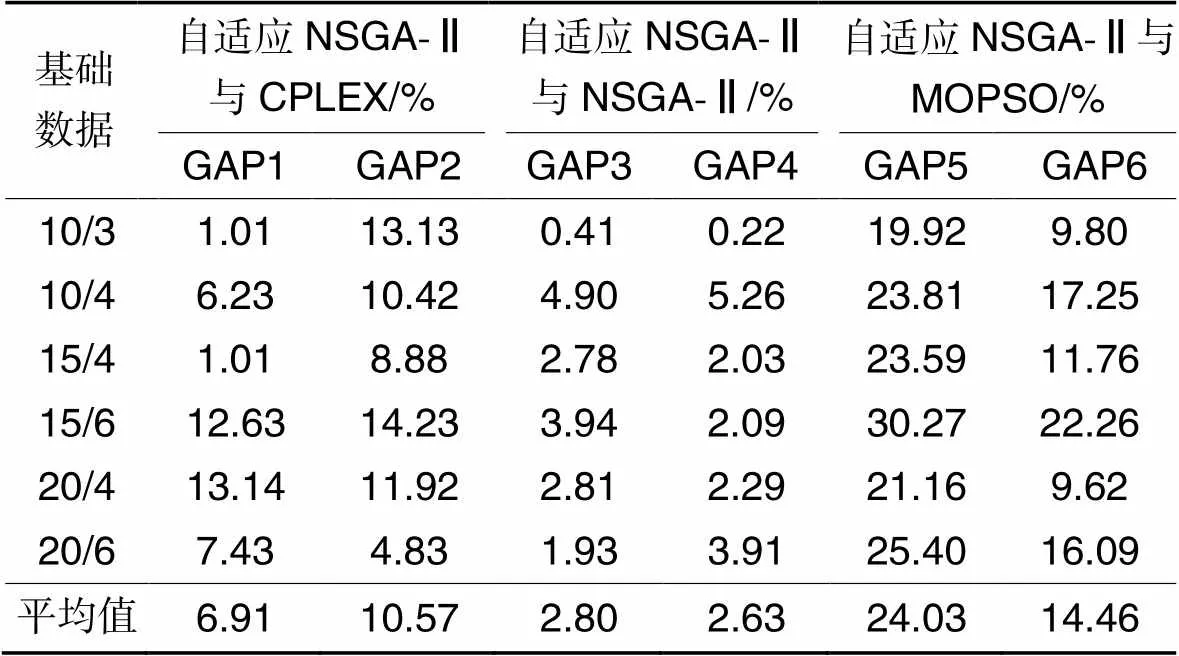
Tab.5 Comparison of difference between algorithm results
注:基础数据由任务数/AGV数组成。
其次对多目标算法的帕累托最优解集进行分析。图7为NSGA-Ⅱ、自适应NSGA-Ⅱ和MOPSO这3种算法某次运行实验5得出的帕累托最优解。如图7所示,可以看出自适应NSGA-Ⅱ的帕累托前沿更靠近原点且解更优,其次是NSGA-Ⅱ,最优解集最差的是MOPSO算法。根据解的聚集情况,自适应NSGA-Ⅱ的解更密集,而NSGA-Ⅱ和MOPSO算法得出的最优解较分散。
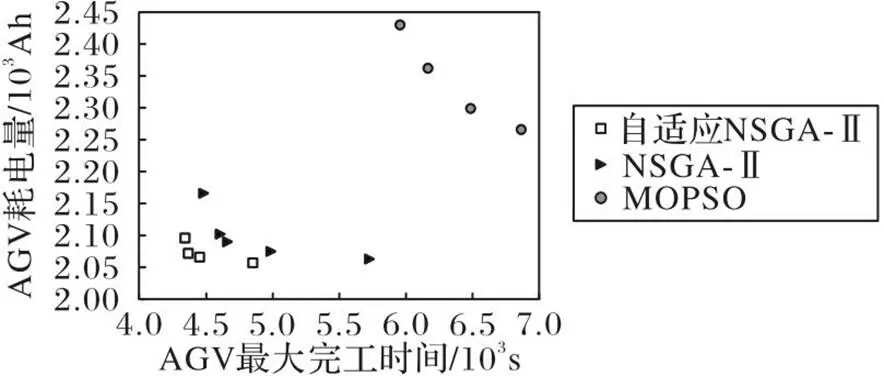
图7 3种算法运行实验5某次得出的帕累托最优解集
综上所述,与NSGA-Ⅱ、CPLEX求解器和MOPSO算法相比,自适应NSGA-Ⅱ在运算时间、计算结果和帕累托最优解集等方面在解决本文问题上具有较大的优势。
4.3 实验研究
AGV作为一种电池供电的运输设备,在执行任务的过程中需要及时进行充电以避免出现拥堵现象,因此AGV充电策略至关重要。对AGV充电策略进行研究时,充电和结束充电时间点是最重要的两个特征,合理的充电策略能够提高AGV工作效率,降低能耗。为研究AGV充电范围和设备数量配置对集装箱整个作业过程的影响,设置两组实验。
实验一 AGV充电策略影响分析。
实验一对安全阈值()和最大可充电池容量()进行参数设计并实验,分别从最大电池容量的[10%,40%]、[70%,100%]组合设计16种充电策略进行实验,并对实验结果从AGV时间利用率、AGV充电时间等几个指标进行分析,计算公式如式(37)所示:
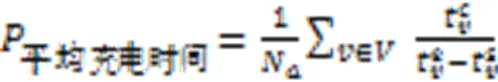
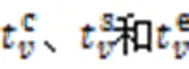
由图8所示,AGV耗电量随的增加而增加,随的增加而减少。
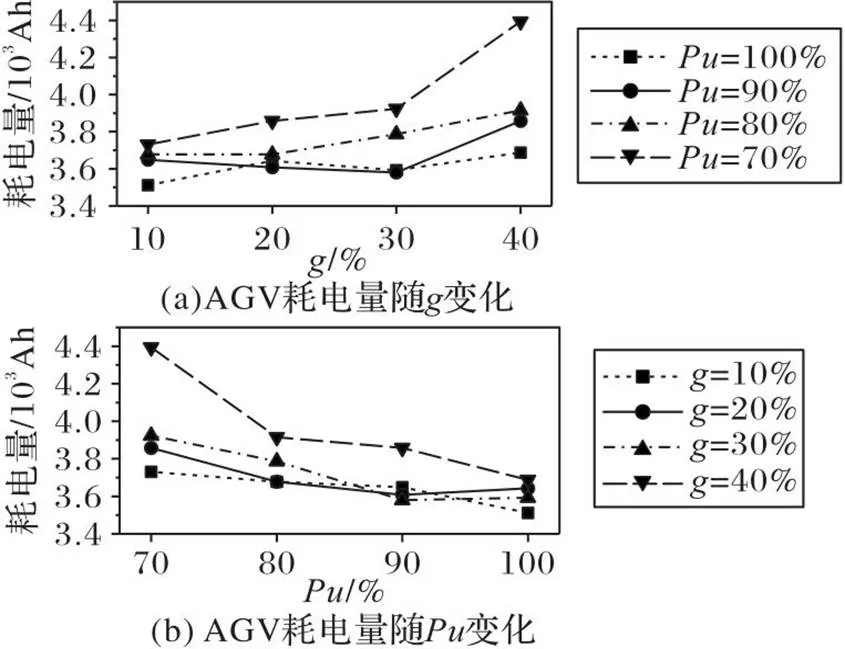
图8 AGV耗电量变化
如图9(a)和图10所示,当从10%增加到40%时,AGV平均单次充电时间减少,使得AGV前往充电站的次数增加,充电时间占比在此情况下呈增加趋势。如图9(b)和图11所示,当从70%增加到100%时,AGV平均单次充电时间增加,AGV在充电站停留的时间增加,因此AGV能够在单次充电后完成更多的集装箱任务,从而降低了AGV的充电次数,使得充电时间占比减少。
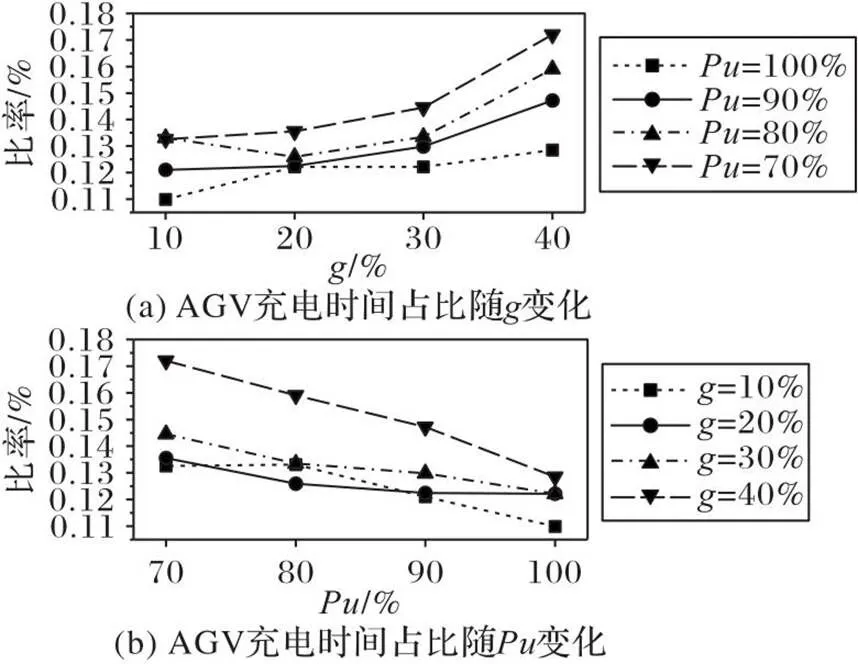
图9 Changes of AGV charging time proportion
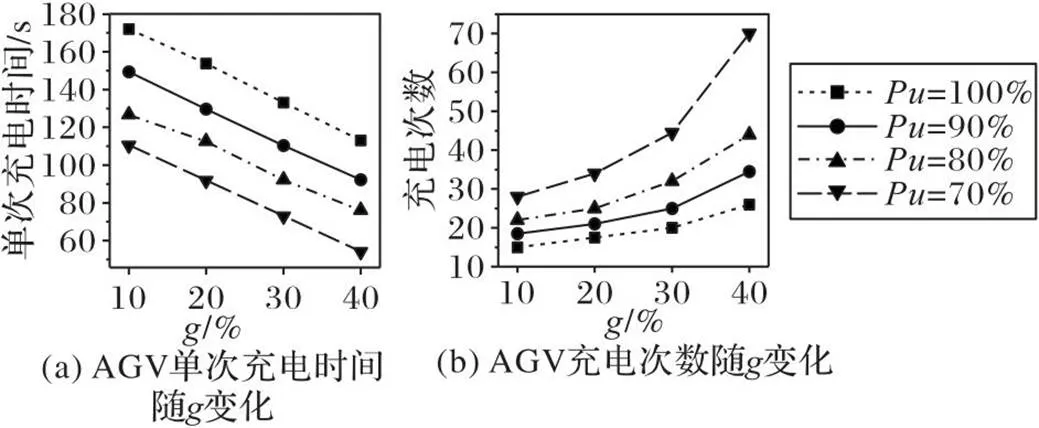
图10 充电时间和充电次数随g变化的情况
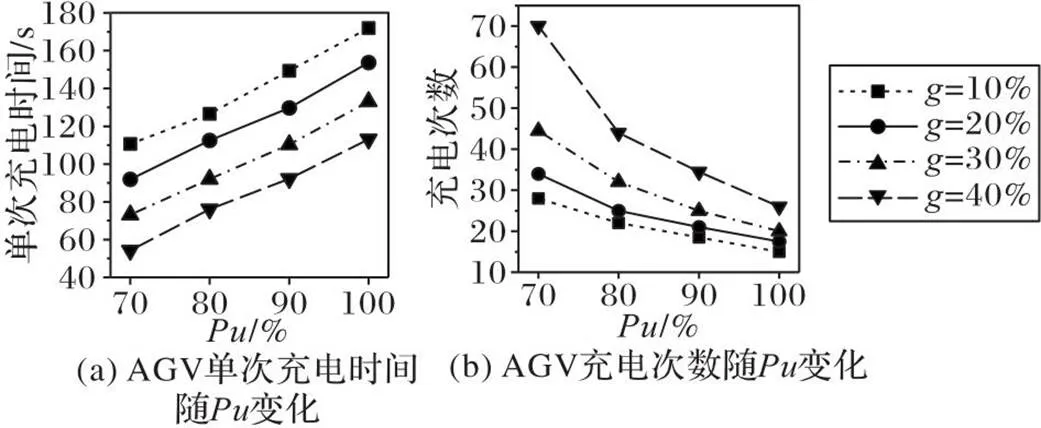
图11 充电时间和充电次数随Pu变化的情况
综上可以看出AGV充电时间占比与充电次数呈正比、与单次充电时间呈反比。相较于充电时间,充电次数对所研究问题下的AGV整体充电时间影响更大,降低AGV充电次数能够减少AGV充电时间占比,提高AGV时间利用率。
实验二 设备数量配比影响分析。
实验二设置任务数为90,岸桥数为3,改变岸桥和AGV数,对岸桥、场桥和AGV数配置进行研究。实验的AGV数分别为3、6和9,场桥数从[3,7]依次分组。通过岸桥时间利用率、场桥时间利用率和AGV时间利用率分析对比,研究岸桥、场桥和AGV配比对集装箱作业任务的影响,公式如式(38)所示:
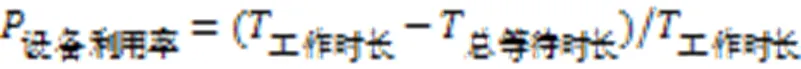
其中:设备利用率表示各设备的时间利用率,工作时长和总等待时长分别表示设备工作总时长和设备总等待时长。实验结果如图12、13所示。
如图12所示,最大完工时间随着AGV数的增加而减少,但场桥数的变化对最大工时间的影响较小。在AGV总耗能方面:当场桥数小于4时,场桥数的增加对AGV耗电量的影响不大;但当场桥数大于4时,AGV耗电量增幅增大。这是因为随着场桥数的增加,AGV执行单位集装箱任务时行驶的距离增加,耗电量增加。
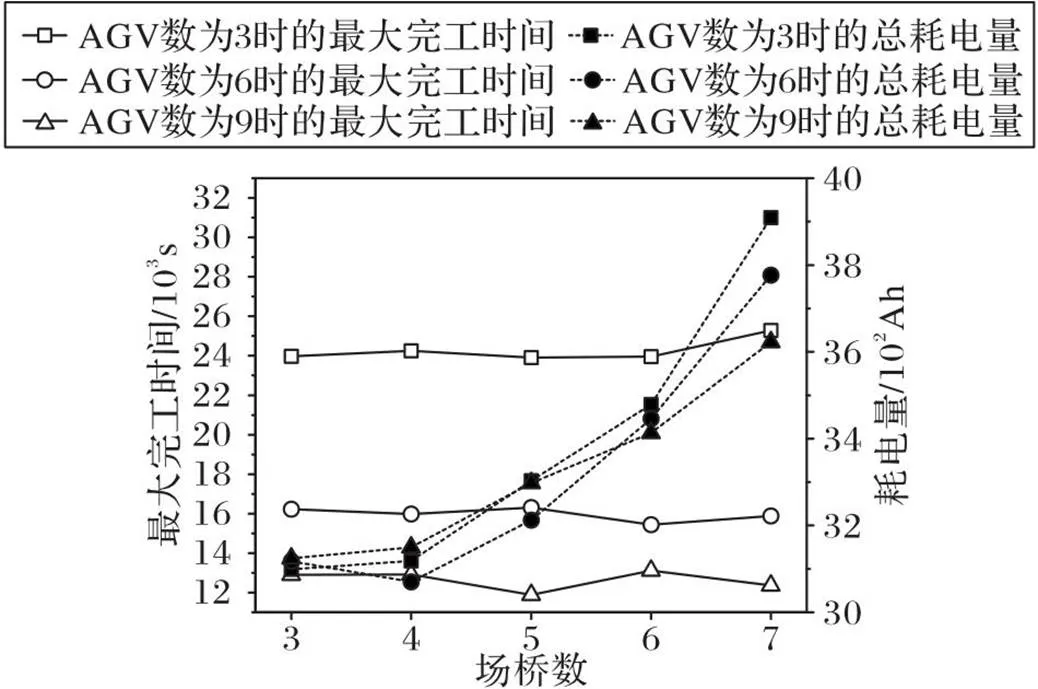
图12 完工时间和AGV耗电量变化
如图13(a)所示,随着AGV数的增加,岸桥利用率增加。这是因为当AGV数增加时,岸桥等待AGV运输集装箱任务的时间缩短,岸桥实际操作时间增加,又因为总完工时间变化不大,则岸桥时间利用率提高,而场桥数的增加对岸桥的时间利用率的影响较小。
如图13(b)所示,随着场桥数的增加,场桥等待时间增加,实际操作时间减少,场桥利用率降低。同时,AGV数的增加使得场桥的利用率增加,这是因为AGV增多后,岸桥的等待时间减少,从而提高了时间利用率。
如图13(c)所示,AGV数的增加反而使得AGV利用率降低。这是因为当任务数一定时,AGV数增加使得AGV在装卸设备下等待的容易产生拥堵,从而增加了AGV的等待时间,使得AGV利用率降低。场桥数的增加使得相同的任务量下,AGV可以将集装箱任务运往其他场桥,从而减少AGV在装卸设备的等待时间。

图13 设备时间利用率变化
综上所述,场桥利用率随着AGV数的增加而增加,随着场桥数的增加而降低;AGV利用率随着AGV数的增加而降低,随着岸桥数的增加而降低。岸桥、场桥和AGV的不同数量配比影响了设备的时间利用率,当岸桥∶场桥∶AGV=3∶3∶9时,场桥的时间利用率最大,为40.69%;当岸桥∶场桥∶AGV=3∶7∶3时AGV的时间利用率最大,为93.2%。
5 结语
在装卸同步的情况下,本文在岸桥、场桥和AGV的集成调度研究中考虑AGV的电量约束,研究了设备的作业序列和AGV调度问题,考虑AGV不同状态下的耗电量、AGV安全阈值等因素,建立多目标混合规划模型最小化AGV最大完工时间和总耗电量。为了减小AGV充电过程对集成调度的影响,本文提出自适应NSGA-Ⅱ,并设计实验验证了模型的可行性。其次,本文对安全阈值和最大电池容量分别组合设计实验,研究AGV不同充电策略对总耗电量、AGV充电时间等的影响,得出了较优的充电策略。最后,研究AGV和岸桥数变化对各设备实际利用率的影响。实验结果表明:1)AGV充电时间受AGV充电次数的影响,可以通过减小安全阈值或增大最大电池容量减少AGV充电时间和耗电量;2)AGV数与岸桥数会影响设备的时间利用率,增加AGV数能够提高场桥和岸桥的时间利用率,而场桥数的增加也能够提高AGV的时间利用率。因此,AGV的数量配置和电池充电阈值能提高设备工作效率、降低耗电量。
然而,本文没有考虑岸桥和场桥在船舶或堆场的翻箱问题;未考虑充电站数量配置、容量限制等问题对AGV充电及调度的影响,当充电站数大于1时,AGV的充电策略都值得进行进一步研究。
[1] LIU D, GE Y-E. Modeling assignment of quay cranes using queueing theory for minimizing CO2emission at a container terminal [J]. Transportation Research Part D: Transport and Environment, 2018, 61(A): 140-151.
[2] 范厚明,岳丽君,李荡,等.考虑路径冲突的AGV配置与调度优化[J].运筹与管理,2020,29(5):43-51(FAN H M, YUE L J, LI D, et al. Optimization of AGV dispatching and configuration considering path conflict [J]. Operations Research and Management Science, 2020, 29(5): 43-51.)
[3] ZHAO Q R, JI S W, GUO D, et al. Research on cooperative scheduling of automated quayside cranes and automatic guided vehicles in automated container terminal [J]. Mathematical Problems in Engineering, 2019, 2019: No. 6574582.
[4] 周玉清,韩晓龙. 双循环策略下岸桥与跨运车的联合调度[J].计算机应用: 2023,43(2):645-653.(ZHOU Y Q, HAN X L. Joint operation of quay crane and straddle carrier under double-cycle strategy [J].Journal of Computer Applications,2023,43(2): 645-653.)
[5] YANG Y, ZHONG M, DESSOUKY Y, et al. An integrated scheduling method for AGV routing in automated container terminals [J]. Computers & Industrial Engineering, 2018, 126: 482-493.
[6] JONKER T, DUINKERKEN M B, YORKE-SMITH N, et al. Coordinated optimization of equipment operations in a container terminal [J]. Flexible Services and Manufacturing Journal, 2019, 33: 281-311.
[7] ZHANG H,QI L, LUAN W, et al. Double-cycling AGV scheduling considering uncertain crane operational time at container terminals[J]. Applied Sciences,2022,12: No.4820.
[8] 陈铮荣. 考虑AGV无冲突路径规划的自动化集装箱码头集成调度[D].北京:北京交通大学, 2020:5-7.(CHEN Z R .Integrated scheduling considering AGV conflict-free path planning in automated container terminal [D]. Beijing: Beijing Jiaotong University, 2020:5-7.)
[9] 吴洪明,邹梦艳. 考虑电池电量约束的自动化码头AGV调度[J]. 起重运输机械, 2021(3): 47-52.(WU H M, ZOU M Y. AGV scheduling of automated terminal considering battery power constraints [J]. Hoisting and Conveying Machinery, 2021(3): 47-52.)
[10] SWEDA T M, DOLINSKAYA I S, KLABJAN D. Optimal recharging policies for electric vehicles [J]. Transportation Science, 2017, 51(2): 457-479.
[11] 周小凡,苌道方,余芳,等. 考虑充电和等待时间的集装箱码头AGV调度[J]. 上海海事大学学报, 2019, 40(3): 1-5,13.(ZHOU X F, CHANG D F, YU F, et al. Scheduling of AGV in container terminals considering charging and waiting time [J]. Journal of Shanghai Maritime University, 2019, 40(3): 1-5,13.)
[12] 张亚琦,杨斌,胡志华,等.自动化码头AGV充电与作业的集成调度研究[J]. 计算机工程与应用, 2017, 53(18): 257-262,270.(ZHANG Y Q,YANG B, HU Z H,et al. Research of AGV charging and job integrated scheduling at automated container terminal [J]. Computer Engineering and Applications, 2017, 53(18): 257-262,270.)
[13] 赵涛,梁承姬,胡筱渊,等. 自动化集装箱码头AGV调度与换电双层模型求解[J]. 大连理工大学学报, 2021, 61(6): 623-633.(ZHAO T, LIANG C J,HU X Y,et al. Solution of AGV scheduling and battery exchange two-layer model for automated container terminal [J]. Journal of Dalian University of Technology, 2021, 61(6): 623-633.)
[14] 陈珲,韩晓龙. 考虑充电策略的自动化码头AGV调度[J]. 上海海事大学学报, 2021, 42(2): 20-25,74.(CHEN H,HAN X L. AGV scheduling of automated terminals considering charging strategy [J]. Journal of Shanghai Maritime University, 2021, 42(2): 20-25,74.)
[15] 傅正堂,胡志华,宗康. 集装箱码头AGV电量非饱和状态下的调度优化[J]. 大连海事大学学报, 2017, 43(3): 58-62.(FU Z T ,HU Z H,ZONG K. Scheduling optimization of container terminal AGV under electricity unsaturation condition [J]. Journal of Dalian Maritime University, 2017, 43(3): 58-62.)
[16] 谢旦岚,郭笛,纪媛,等.自动化码头运输设备充电策略优化的仿真研究[J]. 系统仿真学报, 2020, 32(10): 1927-1935.(XIE D L,GUO D, JI Y,et al. Simulation research on optimization of AGV charging strategy for automated terminal [J]. Journal of System Simulation, 2020, 32(10): 1927-1935.)
[17] DEB K, PRATAP A, AGARWAL S, et al. A fast and elitist multiobjective genetic algorithm: NSGA‑Ⅱ [J]. IEEE Transactions on Evolutionary Computation, 2002, 6(2): 182-197.
[18] SRINIVAS M, PATNAIK L M. Adaptive probabilities of crossover and mutation in genetic algorithms [J]. IEEE Transactions on Systems, Man, and Cybernetics, 1994, 24(4): 656-667.
[19] ZHAN X, XU L, ZHANG J, et al. Study on AGVs battery charging strategy for improving utilization [J]. Procedia CIRP, 2019, 81: 558-563.
[20] COELLO C A C, PULIDO G T, LECHUGA M S. Handling multiple objectives with particle swarm optimization [J]. IEEE Transactions on Evolutionary Computation, 2004,8(3): 256-279.
[21] CHEN J C, CHEN T-L, TENG Y-C. Meta-model based simulation optimization for automated guided vehicle system under different charging mechanisms [J]. Simulation Modelling Practice and Theory, 2021, 106: 102208.
[22] SCHNEIDER M, STENGER A, GOEKE D. The electric vehicle-routing problem with time windows and recharging stations [J]. Transportation Science, 2014, 48(4): 500-520.
Integrated scheduling considering automated guided vehicle charging strategy based on improved NSGA-Ⅱ
XUE Hairong*, HAN Xiaolong
(,,201306,)
Aiming at the power problem of Automated Guided Vehicle (AGV) in the process of performing tasks in Automated Container Terminal (ACT), an integrated scheduling considering AGV charging strategy based on improved Non-dominated Sorting Genetic Algorithm-Ⅱ (NSGA-Ⅱ) was proposed. Firstly, considering the power consumption of AGV under different operating statuses in the integrated scheduling mode of quay crane, yard crane and AGV, a multi-objective mixed programming model with the goal of minimizing the completion time and total power consumption was established. Secondly, to improve the performance of the traditional NSGA-Ⅱ, an adaptive NSGA-Ⅱ was designed and compared with CPLEX solver and Multi-Objective Partical Swarm Optimization (MOPSO) algorithm on performance. Finally, different charging strategies and equipment number ratios of AGV were designed for experimental research. The experimental results of algorithm comparison show that the solution results of the adaptive NSGA-Ⅱ are improved by 2. 80% and 2. 63% respectively on the two objectives proposed compared with NSGA-Ⅱ. The experimental results of applying the adaptive NSGA-Ⅱ to study the ratio of charging strategies and equipment number ratios show that increasing AGV charging number can reduce AGV charging time, and adjusting the ratio of the equipment number to 3:3:9 and 3:7:3 lead to the highest time utilization of yard crane and AGV respectively. It can be seen that the AGV charging strategy and equipment number ratio can influence the terminal integrated scheduling with multiple equipment.
Automated Container Terminal (ACT); Automated Guided Vehicle (AGV); charging strategy; terminal integrated scheduling; adaptive Non-dominated Sorting Genetic Algorithm-Ⅱ (NSGA-Ⅱ); power consumption
TP301.6; TP391.9
A
1001-9081(2023)12-3848-08
10.11772/j.issn.1001-9081.2022121923
2023⁃01⁃04;
2023⁃03⁃21;
2023⁃03⁃22。
薛海蓉(1998—),女,浙江温州人,硕士研究生,主要研究方向:港口运营与管理;韩晓龙(1978—),男,山东潍坊人,副教授,博士,主要研究方向:物流与供应链管理。
XUE Hairong, born in 1998, M. S. candidate. Her research interests include port operation and management.
HAN Xiaolong, born in 1978, Ph. D., associate professor. His research interests include logistics and supply chain management.
