分布式工厂中微型制造单元多目标优化

2024-01-09柳春锋李峥王居凤

计算机应用 2023年12期

柳春锋，李峥，王居凤

分布式工厂中微型制造单元多目标优化

柳春锋1，2*，李峥1，王居凤3

（1.杭州电子科技大学管理学院，杭州 310018； 2.杭州电子科技大学数据科学与智能决策实验中心，杭州 310018； 3.中国计量大学理学院，杭州 310018）（∗通信作者电子邮箱lcf_spring@163.com）

由于各地区存在资源禀赋和产业政策差异，分布式生产对提升制造企业竞争力的作用非常重要，如何利用分布式生产增强大规模定制的柔性是提振消费信心需要解决的重要问题。结合微型制造单元的思想，在多市场多类型产品的分布式混流生产情景下，以最小化人工和转运等运营成本以及最大完工时间为目标，提出分布式工厂构建和生产调度集成模型，以求解微型单元构建、工人和机器配置和各批次产品的生产策略。所提模型能帮助企业实现产能快速释放和合理混流生产，从而实现满足多区域、多产品和差异化需求的分布式制造与销售，并在确保产量的同时降低制造过程中的运营成本。此外，设计多目标粒子群优化（MOPSO）算法求解模型，并将它与非支配排序遗传算法Ⅱ（NSGA‑Ⅱ）和多目标模拟退火（MOSA）算法进行比较。大规模数值实验的结果表明，在相同的运行时间内，MOPSO算法在解集支配覆盖率（CM）、平均理想距离（MID）和最大分散度（MS）这3个指标上均优于NSGA‑Ⅱ和MOSA算法。所提算法可以为微型化分布式生产系统提供高质量的生产运作决策方案。

微型制造单元；分布式制造；生产调度；多目标优化；粒子群优化算法

0 引言

分布式生产指多家工厂（车间）同时参与生产制造，已经应用于钢铁、食品和化工等领域，也受到越来越多学者的关注。多地建设工厂有效利用各地区位、人力和政策等优势，对于企业在激烈市场竞争中降本增效至关重要。近年来许多研究者聚焦分布式生产问题。在传统的调度问题中，一般只考虑工厂内机器之间的作业分配和机器上的作业顺序；而在分布式生产调度问题中，必须额外确定各个工厂之间的作业分配。Fu等［1］总结了近年来学者对分布式生产调度的相关研究，发现以往研究集中在同质化工厂之间的调度，异构工厂间调度应为今后研究方向。Chaouch等［2］提出了一种新的工厂动态分配方法和一种结合局部搜索的混合蚁群优化算法，以解决具有制造时间准则的分布式作业车间调度问题，并通过大规模数值实验，与其他算法的对比结果证明了所提算法的有效性。Xu等［3］提出了一个仿真平台，该平台支持在分布式工厂之间集成各种硬件和软件组件，例如制造设备、基于物理的过程模拟器、系统动态、基于代理和离散事件模拟器，它们通过模拟飞机机翼车间装配，证明模拟集成模型的有效性。

传统制造系统中的制造单元相对固定，无法快速调整适应市场变动，因而一些学者提出微型制造单元的构想，设计了更加灵活的结构适应高度波动的多产品需求。Mohammadi等［4］基于大规模定制产品提出了微型单元制造，即根据产品功能选项对应微型生产单元，将单元采用S型布局，以最小化总材料处理成本、最大化机器之间的总相似性为目标，提出了一种归一化加权方法统一这些目标函数，验证了微型制造单元可以有效地降低成本。Alhawari等［5］提出分层制造单元构建模型，相较于传统单元制造能取得更好效果，在3种需求模式下，以预期利润最大化为目标，证明了分层单元制造系统构建模型的优势。Saraçoğlu等［6］提出一种多阶段单元制造模型，该模型集成了微型单元构建和流水线调度问题，并以一家鞋类制造厂为例，将制造过程分为3个阶段，即持久单元、旋转注塑单元、精整包装单元，通过模型得到生产效率最大化的单元构建和生产调度方案。

优化问题通常存在多个优化目标，且目标之间相互影响，甚至相互冲突，这种问题或存在多种可能的解决方案。对于多目标优化，一般有聚合［4］、字典排序、亚群、帕累托最优和混合应用等方法，其中帕累托最优是应用最广泛的方法。Kaur等［7］提出一种多目标细菌觅食算法，引入优势和非优势前沿面和自适应步长，加速迭代搜索寻优过程，解决多目标调度问题。Yin等［8］建立了一个多目标拆解线平衡模型，同时最小化工作站数量、总拆卸时间、怠速平衡指标和拆卸工具的数量，提出了一种帕累托离散蜂鸟算法。Ayyoubzadeh等［9］研究了车间调度问题，以最小化剩余能源消耗的税收成本和最小化基于软时间窗的工作延误总成本为目标函数，开发了一个双目标数学模型表述该问题，并引入了一种改进型非支配遗传算法Ⅱ（Non-dominated Sorting Genetic Algorithm Ⅱ， NSGA-Ⅱ）。Zhang等［10］提出一种改进的人工蜂群算法以同时优化生产线平衡和工件排产，验证动态节拍时间的合理性，同时在多个维度上将该算法与多目标粒子群和多目标遗传算法比较，验证所提算法的优越性。

可见，以往研究将分布式生产作为传统车间调度的延伸，着眼于多工厂调度或供应链协调，对制造单元微型化的研究主要侧重单元布局角度。本文在多市场场景下提出了分布式工厂中微型单元构建和调度的集成模型，结合了分布式生产的稳定性和微型制造单元的灵活性，可以更加柔性地实施大规模定制产品，从而满足快速变动的市场。同时，设计了多目标粒子群优化（Multi-Objective Particle Swarm Optimization， MOPSO）算法，改进了传统多目标粒子群算法，将决策变量在多个维度的变异对应为粒子在相应方向的移动，粒子群以一定概率向种群最优和个体最优方向移动并快速迭代，这种寻优方式具有较好的收敛和稳定特性。

本文的主要工作如下：

1）通过将制造过程划分为多个阶段，对每个阶段灵活组合多平行机构建微型单元，从而消除生产瓶颈，实现产能快速释放，提高生产效率。

2）将多地区产品需求和资源禀赋差异融入生产制造场景中，使分布式生产的优化更具有全局性。

3）MOPSO算法的个体编码能有效表征高维度的复杂决策变量，有利于求解最优资源配置和生产策略。

1 问题描述与假设

现阶段消费者对个性化的需求日益增加，对制造企业灵活性、敏捷性的要求越来越高。随着人工智能的发展，大规模分布式生产受到越来越广泛的关注。

一方面，传统制造单元大部分依据产品制造全流程形成，随着产品更加多元，制造单元亟须提升灵活性以适应生产需要。传统制造单元导致加工等待时间长，需要将加工过程合理划分为多阶段加工，将机器分阶段组合为微型制造单元，以灵活适应需求变化；同时，生产单元需要合理配置平行机，以提升生产线平衡率，适应小批量生产，提高生产效率。另一方面，分布式生产对于制造企业应对风险、保障市场竞争力至关重要。企业在多地区建厂也存在人力和转运等成本的差异，需要通过合理决策提升制造企业的稳定性和适应性。因此，本文的优化问题将微型单元和分布式生产结合，形成一个集成模型解决多平行机的微型制造单元构建、分布式生产工厂构建和生产调度问题。此问题基于以下假设：

1）区域。已知区域数、区域中包含的产品需求来源、加工工厂、加工所需人力和机器等资源。不同区域对不同类型产品需求量存在差异，不同区域间距不同，劳动力雇佣成本各不相同。同一区域内的运输时间远小于任意产品单阶段加工时间，所以运输时间和成本可忽略不计。

2）工厂。工厂可能分布于不同区域，工厂在不同区域的建厂成本可能不同，最大建厂可用面积因地制宜。各区域建厂数存在上限，工厂的产品可以销往本地或外地区域。

3）机器。机器类型数已知，每种类型机器仅对应一道加工工序，每种类型产品的机器加工时间可能不同。不考虑机器启动或故障等影响生产进度因素。

4）产品。已知产品类型数和各类型产品的需求量。各类型产品的需求量远大于各类型平行机数。

5）工序。各类型产品的加工包含若干道工序，其中每道工序需要相应的机器类型加工；如果某类型机器存在多台平行机，则将相应产品平均分配至平行机加工。每个产品的每道工序的处理一旦开始就不能中断。两台不同机器之间的产品安装和卸载时间远小于处理时间，可以忽略不计。

6）批次。各种类型产品中每批次数相同，且仅与产品类型相关。批次数不超过任意区域需求。产品按批次生产运输，当产品需求量不足一个批次，按照一个批次计算。

7）生产阶段。生产工序依据实践经验可划分为多个生产阶段，每阶段至少包含一种机器类型。各产品类型各批次的各生产阶段任务应在某个微型单元处理。

8）微型制造单元。每个微型单元仅可完成某一个生产阶段的产品加工，配置该阶段所有机器类型一台，如果配置多台平行机，平行机数不超出上限。

9）工人。工人包含多种技能水平，不同技能水平的工人拥有不同的加工速度。技能水平及区域位置决定着雇佣成本。要求一台机器由一位工人操作。

2 模型建立

2.1　参数介绍

1）输入变量。

2）决策变量。

目前宏济堂中医药文化产业园区已建成多条不同主题的游览线路以适合不同群体的需求，旅游配套设施不完善是园区的短板，逐渐设置明确的路标、导览图、标示牌、景物介绍牌、安全提示牌等标识。园区内设有多辆观光游览车、摆渡车等，主题展区均配备充足的厕所，男女厕位比例合理。特色旅游商品主要有阿胶、阿胶枣、阿胶山楂、阿胶速溶粉、雪梨膏等企业自有产品。园区内虽然有高中低不同档次的餐厅，但与员工、游客期望的差距依然巨大，调查问卷对应得分是2.72和3.56，均为所有项目中的最低分。

3）中间变量。

2.2　数学模型

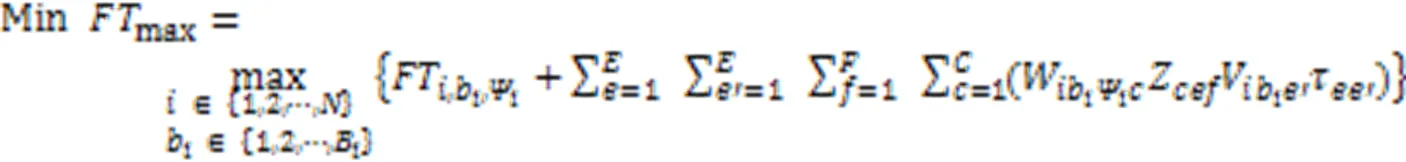
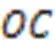
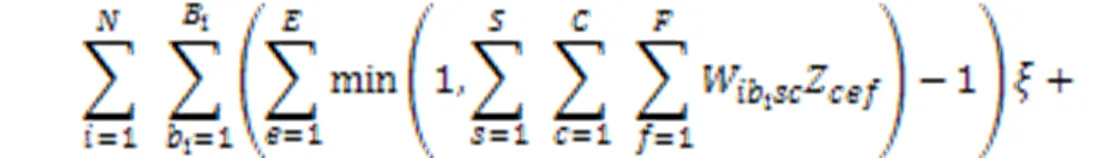
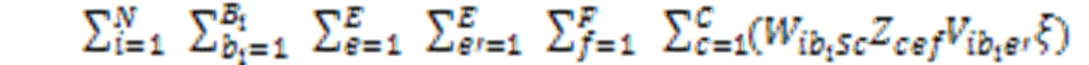
s.t.

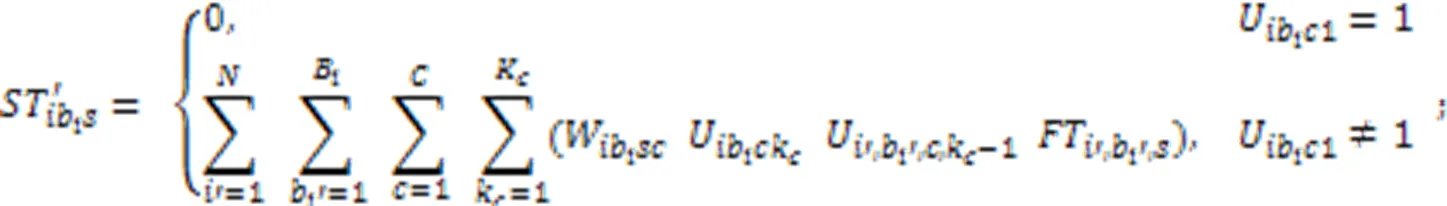
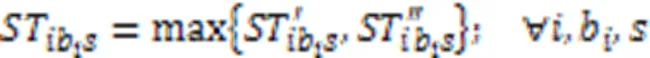
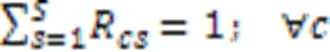
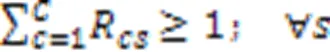
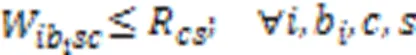
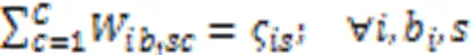
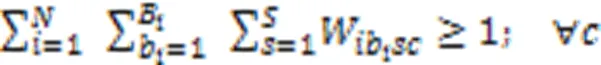
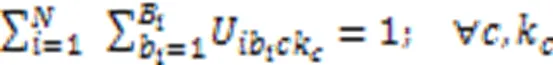
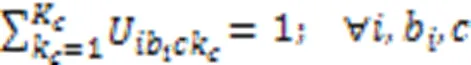
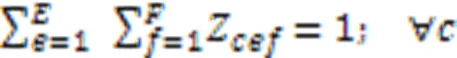
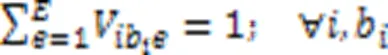
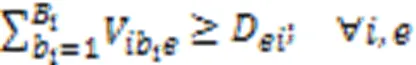
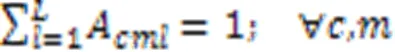
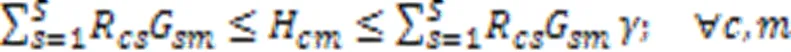
目标函数式（1）表示最大完工时间，其中包含不同阶段制造单元间转运时间以及生产完工后到达需求所在区域的运输时间。

目标函数式（2）表示运营成本，包含以下四项：第一项为固定投资成本，是不同地域工厂数、工厂面积与单位面积固定成本的乘积；第二项为机器成本，是每种类型机器价格与所有微型单元中数和的乘积；第三项为人工成本，是不同区域中不同技能水平工人数与该区域中人工雇佣成本的乘积；第四项为转运成本，包含不同阶段制造单元间的转运成本和生产完工后到达需求所在区域的转运成本。

约束式（3）确保任意产品任意批次任意阶段所在微型单元释放资源的时刻等于该单元中更高优先级任务的完成时间，优先级最高的任务可直接开始加工；约束式（4）确保任意产品任意批次任意阶段的任务抵达生产单元时间等于上一阶段任务的完工时间与运输时间之和，任意产品任意批次第一阶段的任务可直接开始加工；约束式（5）确保任意产品任意批次任意阶段任务的开始加工时间不早于微型单元资源释放时间和该任务抵达时间；约束式（6）确保任意产品任意批次任意阶段任务的完成时间等于它的开始时间与加工时间之和，其中加工时间为该批次产品数与该批次加工瓶颈时间的乘积，瓶颈时间为产品在该阶段的工序的加工时长与机器数和工人效率系数乘积之比的最大值；约束式（7）确保任意微型单元中仅能加工某一个生产阶段的任务；约束式（8）确保任意生产阶段的任务至少配置一个可用微型单元；约束式（9）确保任意产品的任意批次在任意阶段仅能分配至具备该阶段生产能力的微型单元；约束式（10）确保任意产品任意批次仅将需要加工的生产阶段分配至微型单元，且只能分配至某一个微型单元加工；约束式（11）确保任意微型单元至少加工一个批次产品；约束式（12）确保任意单元中所有产品所有批次需要排定优先级；约束式（13）确保任意单元中所生产的任意产品的任意批次仅占一个优先级；约束式（14）确保任意微型单元仅能分配至唯一工厂；约束式（15）确保任意产品的任意批次仅销往某一区域；约束式（16）确保任意产品的任意区域的需求都被满足；约束式（17）确保任意微型单元中任意类型机器上分配一种类型工人操作；约束式（18）确保任意微型单元处理某阶段任务所需机器类型数不少于1且不超过平行机数上限；约束式（19）确保任意区域的任意工厂中所分配机器占地面积总和不得超过该工厂可使用面积；约束式（20）定义了决策变量类型。

3 本文算法

3.1　MOPSO算法

粒子群优化（Particle Swarm Optimization， PSO）是一种应用广泛的智能优化算法［10-12］，算法最初受到飞鸟集群活动规律性启发，进而利用群体智能建立了一个简化模型。粒子群算法在对动物集群活动行为观察基础上，利用群体中的个体对信息的共享，使整个群体的运动在问题求解空间中产生从无序到有序的演化过程，从而获得最优解。

经典PSO算法常用于连续空间求解［13］，但本文模型中包含的7个决策变量均为多维度离散变量，同时模型的两个优化目标为时间和成本，属性不同，使用传统算法思路求解存在收敛慢、易陷入局部最优解等诸多问题，因此决策变量编码和寻优路径设计将直接决定求解效率和所求解的质量。本文为构建的多目标模型提出了离散型MOPSO算法。算法的群体中包含多个粒子（可行解），并标记群体和个体最优方向（即决策变量），寻优过程中每个粒子以一定的概率朝各个方向移动（即变异），并朝个体和群体最优方向进行多次移动，将产生的粒子放入种群，通过快速非支配排序和拥挤度排序更新种群。

3.1.1粒子编码

粒子采用7个多维解结构的组合［14］，每个多维解结构分别代表不同的决策变量。

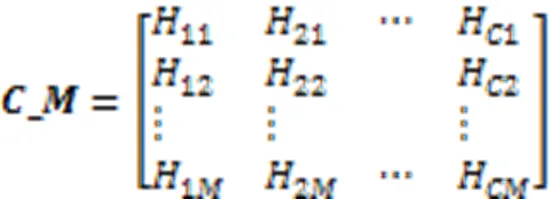
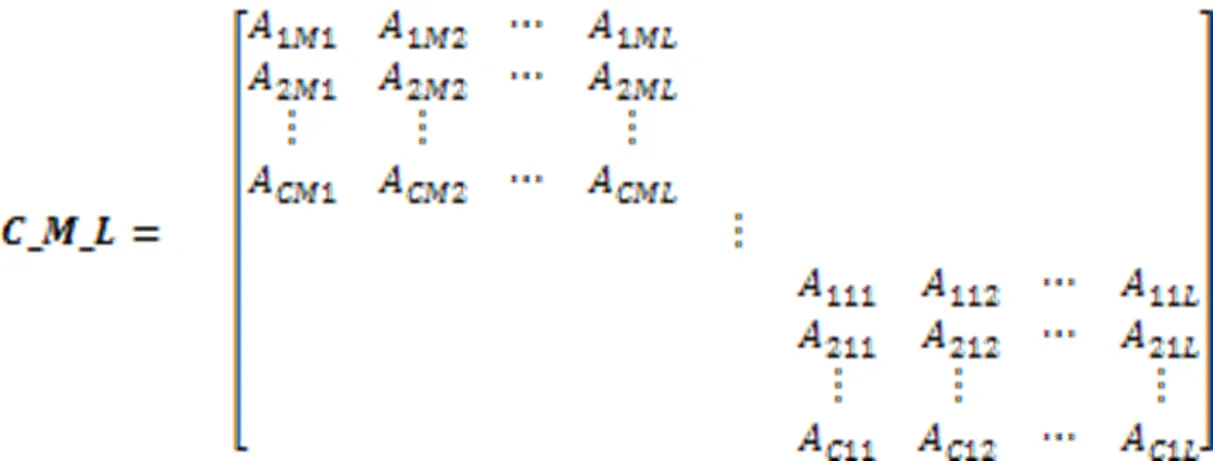
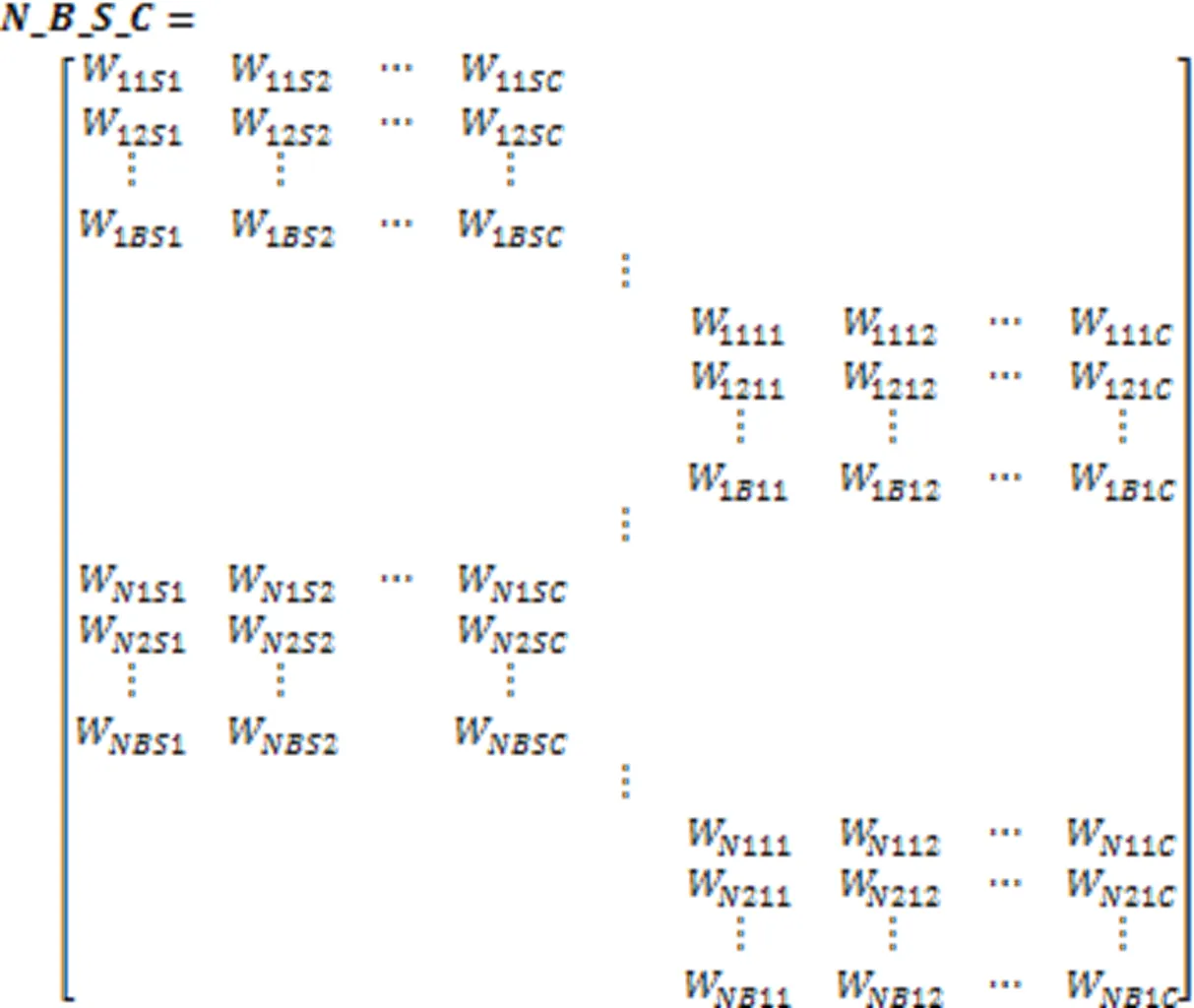
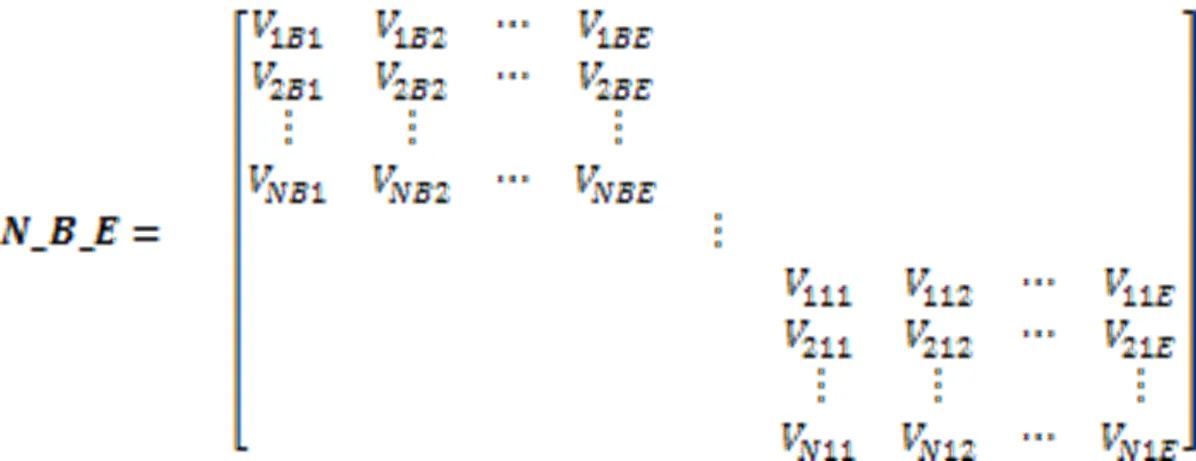
结合以上七个部分，粒子（解决方案）的编码如下所示：

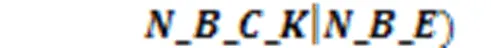
3.1.2算法实施

MOPSO算法系数的选取综合考虑算法运行时间、收敛速度、解的质量等要素，系数均为多次实验调试得到的较理想的值。MOPSO算法流程如下：

7） End for

11） End for

15） End for

18） End if

19） End for

24） End while

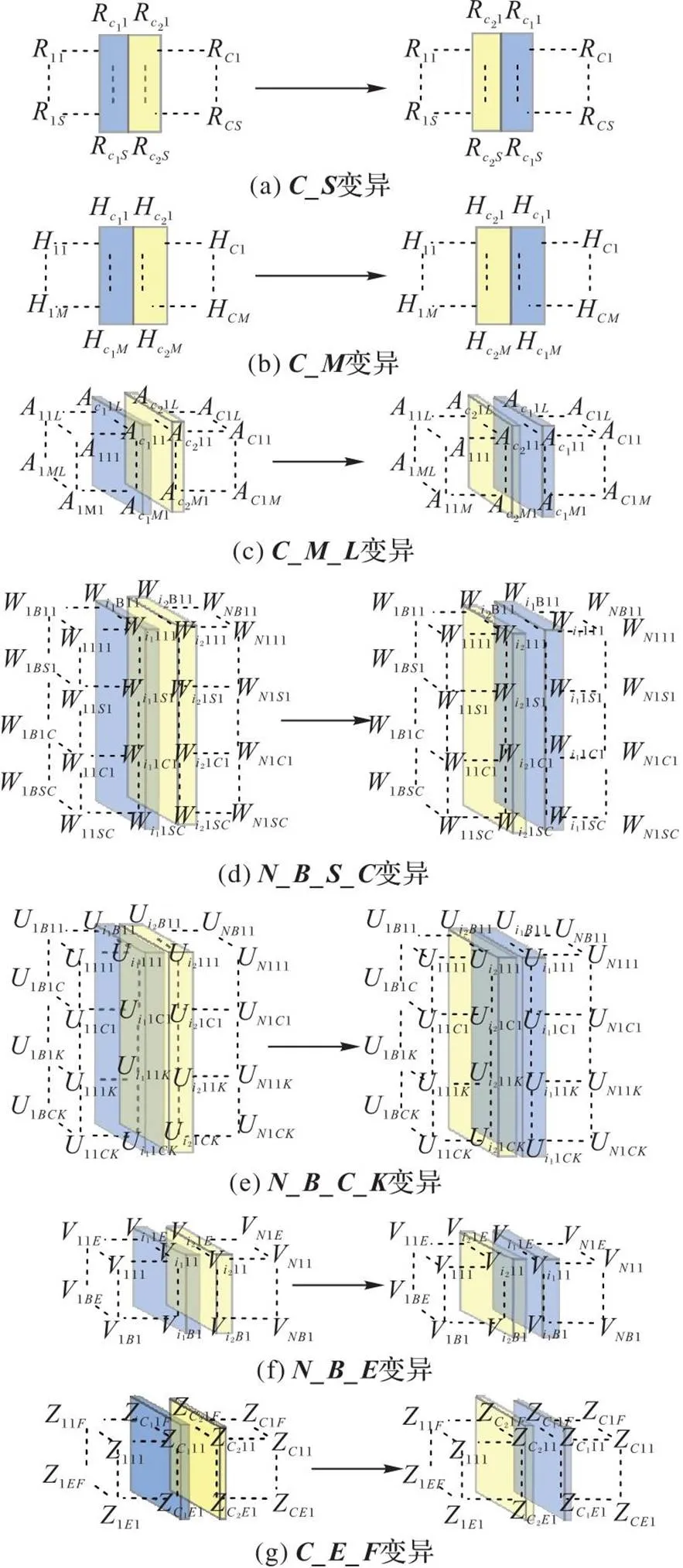
图1　粒子变异

3.2　多目标优化相关术语

1）多目标优化基础模型。

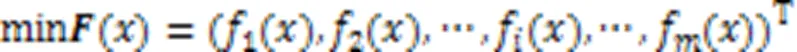
2）帕累托支配。

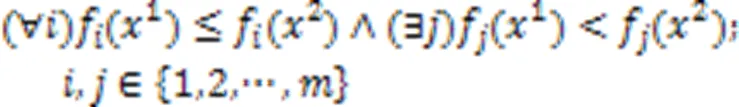
3）非支配解。

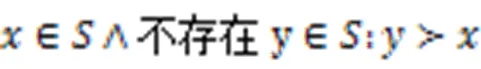
4）帕累托最优解集。

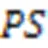
5）帕累托前沿面。

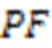
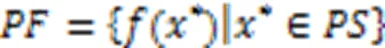
4 实验与结果分析

4.1　参数

本文通过算例实验对比MOPSO、NSGA-Ⅱ［9，16］和多目标模拟退火（Multi-Objective Simulated Annealing， MOSA）算法［17］的性能。实验在64位戴尔个人笔记本电脑上运行，时钟脉冲频率为1.8 GHz，RAM为6 GB。两种算法均通过C++编写，用Microsoft Visual C++ 8.0编译器编译，并在Microsoft Windows 7操作系统下测试。

实验种群规模为50，变量取值情况见表1，其中部分参数是给定数值，部分参数在极值范围内随机生成。通过实验对比两种算法性能差异，图2显示了相同运行时间内两种算法所得解集的帕累托前沿面，可以看出MOPSO算法前沿面明显优于NSGA-Ⅱ和MOSA算法。下文通过更加科学的指标统计，并通过大规模数值实验进一步验证算法性能。

4.2　多目标优化解的评价

由于多目标优化算法存在多维决策变量，本文将从收敛性和延展性［10］出发，通过两种多目标优化算法所得解集质量验证算法的优劣，其中：收敛性通过两种算法帕累托前沿面的覆盖率进行比较，延展性根据最大分散度指标衡量。

4.2.1收敛性

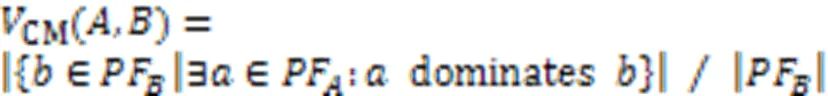
4.2.2延展性

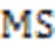
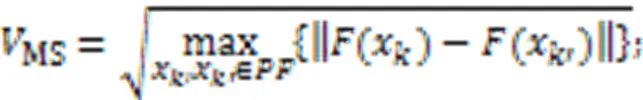
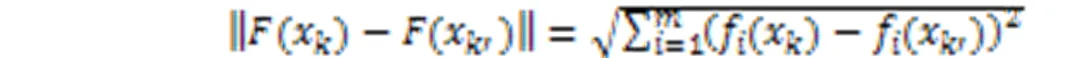
4.2.3综合性指标

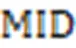
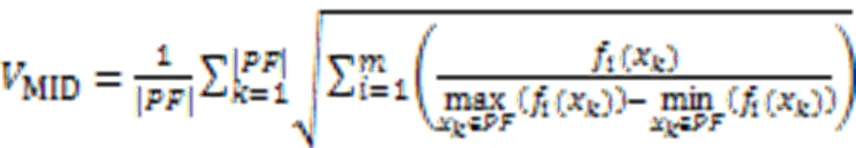
4.3　数值实验

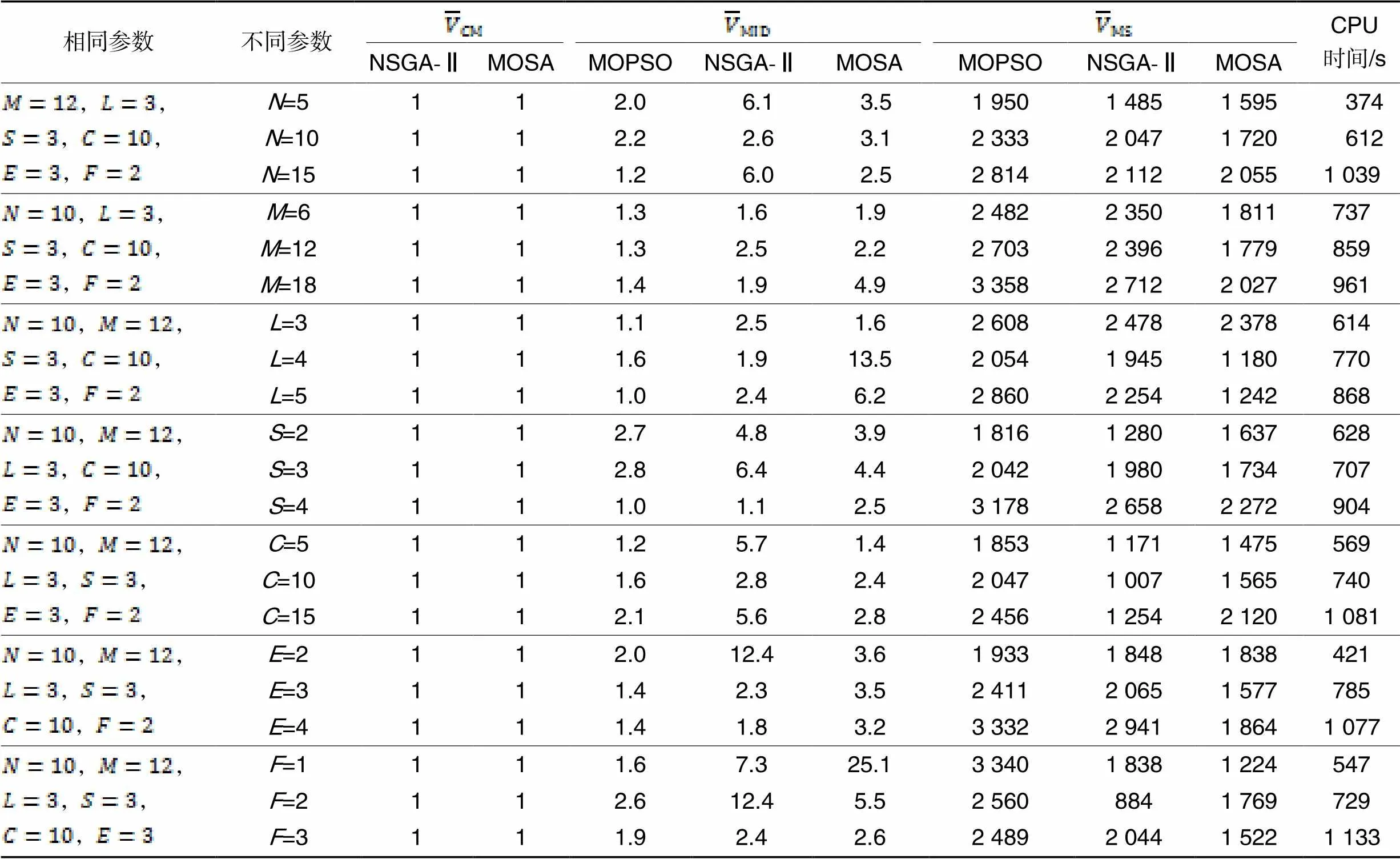
表2　MOPSO算法、NSGA-Ⅱ和MOSA算法在不同参数取值下的性能对比

5 结语

本文分析了多区域建设工厂满足各区域的多类产品差异性需求的生产场景，研究了合理划分加工过程、将机器组合为微型单元，并使它集成于分布式制造系统。以最小化人工和转运等运营成本和最小化最大完工时间作为双目标，提出了一个微型单元构造和生产调度的集成模型，该模型可得出多区域的工厂中工人和机器配置以及各批次产品的生产策略。本文提出了MOPSO算法，种群中粒子能以一定的概率多次向个体历史最优值、种群最优值学习，通过快速非支配排序和拥挤度排序不断更新迭代，使得种群趋向最优值。算例和大规模数值实验结果显示：MOPSO算法在3个评价指标（即解集支配覆盖率、平均理想距离和最大分散度）上均优于应用广泛的NSGA-Ⅱ和MOSA算法，可见MOPSO算法在处理高维多目标问题时，可快速收敛并具有更好的寻优性能。未来可以进一步研究分布式微型制造单元系统的实时布局，为大规模个性化定制创造有利的技术条件。

[1] FU Y， HOU Y， WANG Z， et al. Distributed scheduling problems in intelligent manufacturing systems［J］. Tsinghua Science and Technology， 2021， 26（5）： 625-645.

[2] CHAOUCH I， DRISS O B， GHEDIRA K. A novel dynamic assignment rule for the distributed job shop scheduling problem using a hybrid ant-based algorithm［J］. Applied Intelligence， 2019， 49（5）： 1903-1924.

[3] XU D， NAGESHWARANIYER S S， SON Y J. A service-oriented simulation integration platform for hierarchical manufacturing planning and control［J］. International Journal of Production Research， 2016， 54（23）： 7212-7230.

[4] MOHAMMAD M， FORGHANI K. Designing cellular manufacturing systems considering S-shaped layout ［J］. Computers and Industrial Engineering， 2016， 98： 221-236.

[5] ALHAWARI O I， SÜER G A， BHUTTA M K S. Operations performance considering demand coverage scenarios for individual products and products families in supply chains ［J］. International Journal of Production Economics， 2021， 233： No.108012.

[6] SARAÇOĞLU İ， SÜER G A， GANNON P. Minimizing makespan and flowtime in a parallel multi-stage cellular manufacturing company［J］. Robotics and Computer-Integrated Manufacturing， 2021， 72： No.102182.

[7] KAUR M， KADAM S. A novel Multi-Objective Bacteria Foraging Optimization Algorithm （MOBFOA） for multi-objective scheduling［J］. Applied Soft Computing， 2018， 66： 183-195.

[8] YIN T， ZHANG Z， JIANG J. A Pareto-discrete hummingbird algorithm for partial sequence-dependent disassembly line balancing problem considering tool requirements［J］. Journal of Manufacturing Systems， 2021， 60： 406-428.

[9] AYYOUBZADEH B， EBRAHIMNEJAD S， BASHIRI M， et al. Modelling and an improved NSGA-Ⅱ algorithm for sustainable manufacturing systems with energy conservation under environmental uncertainties： a case study ［J］. International Journal of Sustainable Engineering， 2021， 14（3）： 255-279.

[10] ZHANG W， HOU L， JIAO R J. Dynamic takt time decisions for paced assembly lines balancing and sequencing considering highly mixed-model production： an improved artificial bee colony optimization approach ［J］. Computers and Industrial Engineering， 2021， 161： No.107616.

[11] XUE B， ZHANG M， BROWNE W N. Particle swarm optimization for feature selection in classification： a multi-objective approach［J］. IEEE Transactions on Cybernetics， 2013， 43（6）： 1656-1671.

[12] FENG H， DA W， XI L， et al. Solving the integrated cell formation and worker assignment problem using particle swarm optimization and linear programming［J］. Computers and Industrial Engineering， 2017， 110： 126-137.

[13] ADINARAYANAN A， DINESH S， BALAJI D S， et al. Design of machine cell in cellular manufacturing systems using PSO approach［J］. Materials Today： Proceedings， 2021， 46（Pt 9）： 3951-3955.

[14] LIU C， WANG J， ZHOU M. Reconfiguration of virtual cellular manufacturing systems via improved imperialist competitive approach［J］. IEEE Transactions on Automation Science and Engineering， 2019， 16（3）： 1301-1314.

[15] DEB K， PRATAP A， AGARWAL S， et al. A fast and elitist multiobjective genetic algorithm： NSGA‑Ⅱ［J］. IEEE Transactions on Evolutionary Computation， 2002， 6（2）： 182-197.

[16] 季宁，张卫星，于洋洋，等.基于最优拉丁超立方抽样方法和NSGA‑Ⅱ算法的注射成型多目标优化［J］. 工程塑料应用， 2020， 48（3）： 72-77.（JI N， ZHANG W X， YU Y Y， et al. Multi-objective optimization of injection molding based on optimal Latin hypercube sampling method and NSGA‑Ⅱ algorithm［J］. Engineering Plastics Application， 2020， 48（3）： 72-77.）

[17] 姜东，唐秋华，李梓响，等.多目标模拟退火算法求解混装线平衡与排序［J］. 机械设计与制造， 2018（9）： 189-192.（JIANG D， TANG Q H， LI Z X， et al. Multi-objective simulated annealing algorithm for balancing and sequencing of mixed-model assembly line ［J］. Machinery Design & Manufacture， 2018（9）： 189-192.）

[18] LU C， GAO L， PAN Q， et al. A multi-objective cellular grey wolf optimizer for hybrid flowshop scheduling problem considering noise pollution ［J］. Applied Soft Computing， 2019， 75： 728-749.

[19] SHABANI-NAEENI F， GHASEMY YAGHIN R. Integrating data visibility decision in a multi-objective procurement transport planning under risk： a modified NSGA‑Ⅱ［J］. Applied Soft Computing， 2021， 107： No.107406.

Multi-objective optimization of minicells in distributed factories

LIU Chunfeng1，2*， LI Zheng1， WANG Jufeng3

（1，，310018，；2，，310018，；3，，310018，）

Due to differences in resource endowments and industrial policies among different regions， the role of distributed production in improving the competitiveness of manufacturing enterprises is very important. How to use distributed production to enhance the flexibility of mass customization is an important problem to be solved to boost consumer confidence. Combined with the idea of minicells — small manufacturing cells， in the distributed mixed production scenario with the multi-market and multi-product characteristics， an integrated model of distributed factory construction and production scheduling was proposed with the objectives to minimize the operating costs （e.g.， labor and transportation costs） and minimize the makespan. By the proposed model， the minicell construction， worker and machine configuration， as well as production strategies for each batch of products were able to be solved. With the help of the proposed model， the enterprises were able to realize the quick release of production capacity and reasonable mixed flow production， so as to realize distributed manufacturing and sales that meet the multi-region， multi-product， and differentiated needs， and reduce the operating cost in the manufacturing process while guaranteeing the throughput. In addition， a Multi-Objective Particle Swarm Optimization （MOPSO） algorithm was designed to solve the proposed model， and was compared with Non-Dominated Sorting Genetic Algorithm Ⅱ （NSGA-Ⅱ） and Multi-Objective Simulated Annealing （MOSA） algorithm. The results of extensive numerical experiments show that MOPSO algorithm outperforms NSGA-Ⅱ and MOSA algorithm with the same running time in terms of three metrics： C-Metric （CM）， Mean Ideal Distance （MID） and Maximum Spread （MS）. The proposed algorithm can provide a high-quality decision-making scheme of production operation for the miniaturized distributed production system.

minicell; distributed manufacturing; production scheduling; multi-objective optimization; Particle Swarm Optimization (PSO) algorithm

This work is partially supported by Foundation of Humanities and Social Sciences of Ministry of Education （21YJA630065）.

LIU Chunfeng， born in 1977， Ph. D.， professor. His research interests include production system optimization， intelligent optimization algorithm.

LI Zheng， born in 1995， M. S. candidate. His research interests include production system optimization， intelligent optimization algorithm.

WANG Jufeng， born in 1977， Ph. D.， associate professor. Her research interests include mathematical modeling， intelligent optimization algorithm.

TP30； F406.2

1001-9081（2023）12-3824-09

10.11772/j.issn.1001-9081.2022111772

2022⁃12⁃07；

2023⁃06⁃19；

2023⁃06⁃28。

教育部人文社会科学研究规划基金资助项目（21YJA630065）。