基于Fisher score与模糊邻域熵的多标记特征选择算法

2024-01-09孙林马天娇薛占熬

计算机应用 2023年12期

孙林，马天娇，薛占熬

孙林1*，马天娇2，薛占熬2，3

（1.天津科技大学人工智能学院，天津 300457； 2.河南师范大学计算机与信息工程学院，河南新乡 453007； 2.智慧商务与物联网技术河南省工程实验室（河南师范大学），河南新乡 453007）（∗通信作者电子邮箱sunlin@htu.edu.cn）

针对Fisher score未充分考虑特征与标记以及标记之间的相关性，以及一些邻域粗糙集模型容易忽略边界域中知识粒的不确定性，导致算法分类性能偏低等问题，提出一种基于Fisher score与模糊邻域熵的多标记特征选择算法（MLFSF）。首先，利用最大信息系数（MIC）衡量特征与标记之间的关联程度，构建特征与标记关系矩阵；基于修正余弦相似度定义标记关系矩阵，分析标记之间的相关性。其次，给出一种二阶策略获得多个二阶标记关系组，以此重新划分多标记论域；通过增强标记之间的强相关性和削弱标记之间的弱相关性得到每个特征的得分，进而改进Fisher score模型，对多标记数据进行预处理。再次，引入多标记分类间隔，定义自适应邻域半径和邻域类并构造了上、下近似集；在此基础上提出了多标记粗糙隶属度函数，将多标记邻域粗糙集映射到模糊集，基于多标记模糊邻域给出了上、下近似集以及多标记模糊邻域粗糙集模型，由此定义模糊邻域熵和多标记模糊邻域熵，有效度量边界域的不确定性。最后，设计基于二阶标记相关性的多标记Fisher score特征选择算法（MFSLC），从而构建MLFSF。在多标记K近邻（MLKNN）分类器下11个多标记数据集上的实验结果表明，相较于ReliefF多标记特征选择（MFSR）等6种先进算法，MLFSF的平均分类精度（AP）的均值提高了2.47～6.66个百分点；同时，在多数数据集上，MLFSF在5个评价指标上均能取得最优值。

多标记学习；特征选择；Fisher score；多标记模糊邻域粗糙集；模糊邻域熵

0 引言

目前，维度灾难是多标记学习面临的重要挑战之一［1］。特征选择是大数据降维的一种有效手段，可以分为过滤法、包裹法和嵌入法等［2］。过滤法筛选特征集，使用学习算法训练，它的过程与学习算法无关，可以快速剔除噪声特征，计算效率较高、通用性强，所选特征子集冗余度小，适用于大规模数据集［3］。包裹法依赖于所选择的学习算法，使用分类器性能评价特征重要程度，特征子集的分类性能较好；但是不适合处理高维数据，通用性弱，计算复杂度高［4］。嵌入法结合特征选择过程和分类器训练过程；但是过度依赖具体的学习算法，会出现过拟合现象，缺乏通用性［5-6］。因此，为了有效处理高维多标记数据集，提升计算效率和避免出现过拟合情况，使用过滤法设计多标记特征选择。

Fisher score是一种经典的过滤式特征选择算法，主要思想是利用距离度量鉴别使类内距离尽可能小、类间距离尽可能大的特征［7］。该算法具有可操作性强、精度高、计算成本低等优点，目前已有较多的研究：Guyon等［8］提出了基于Fisher score的特征选择算法应用于基因分类；Günes等［9］采用Fisher score进行多重分类，并将得分均值作为特征选择阈值；孙林等［10］针对非平衡数据采用Fisher score选择高分的特征实施降维。但是，上述算法未考虑特征之间的相关性。Hancer等［11］使用ReliefF和Fisher score进行特征选择，考虑了特征与类别标记的相关性；吴迪等［12］结合最大信息系数和Fisher score进行特征选择。但是，上述2种算法未考虑类之间的差异性。同时，上述5种使用Fisher score的特征选择算法只能处理单标记中的类别型数据。随着Fisher score在单标记的广泛应用，在多标记方面的研究也逐渐出现：汪正凯等［7］考虑由于极值带来的类别中心与实际中心的偏差，提出一种结合中心偏移和多标记集合关联性的多标记Fisher score特征选择算法；但是没有考虑特征之间的相关性。Sun等［6］构建了正、负标记之间的互信息以考虑标记之间的相关性，设计了一种基于互信息的Fisher score多标记特征选择算法；但是标记的正、负数通常不平衡，也没有考虑特征与标记的相关性。受上述研究启发，本文为了考虑标记与特征的相关性、标记之间的相关性，构建了标记之间的二阶关系，与Fisher score结合，对多标记数据进行特征选择预处理，有效提升算法分类性能。

邻域粗糙集作为一种过滤式策略在多标记学习和分类中得到了广泛的应用［1］：段洁等［13］提出了一种处理连续数据和数值数据的多标记邻域粗糙集特征选择算法，但该算法耗时，且邻域半径需通过手动设置步长，无法达到最优效果；为了克服这个缺点，Lin等［14］推广邻域信息熵多标记学习，提出了一种基于邻域互信息的多标记特征选择算法；Liu等［15］针对流式多标记数据设计了基于邻域粗糙集的特征选择算法；Huang等［16］提出了一种基于邻域粗糙集的改进的最大相关和最小冗余的多标记特征选择算法；Sun等［1］利用Jaccard相关系数构建了特征权值公式，进而设计了一种基于多标记ReliefF和邻域互信息的多标记特征选择算法；Wu等［17］通过考虑标记相关性，将相关标记划分为多个标记子集，进而将标记相关性引入邻域粗糙集模型。然而，多标记邻域粗糙集使用邻域粒近似描述决策等价类，无法描述模糊背景下实例的不确定性。Chen等［18］为处理多种类型的数据，研究了基于变精度模糊邻域粗糙集的多标记特征选择算法；但是，该算法仍存在邻域半径参数需要手动设置的问题。Sun等［19］提出了一种基于多标记模糊邻域粗糙集和最大相关性最小冗余度的特征选择算法，用于处理缺失标记的多标记数据；但该算法的求解过程需要大量的矩阵运算，时间代价较高。Xu等［20］引入模糊邻域近似精度考虑上近似中的不确定性，建立了多标记模糊邻域条件熵；但该算法需要遍历所有参数，以确定每个数据集的最佳模糊邻域半径，且实验数据集的维度较低。为解决上述问题，本文采用分类间隔得到自适应的邻域粒半径与邻域类，构造多标记邻域上、下近似集，挖掘边界域邻域粒包含的不确定信息并构造多标记粗糙隶属度函数，构建多标记模糊邻域粗糙集模型，由此基于模糊邻域熵研究多标记邻域决策系统的不确定性度量。

本文的主要工作如下：

1）为了考虑特征与标记以及标记之间的相关性，利用最大信息系数衡量特征与标记之间的关系，构建特征与标记关系矩阵；使用修正余弦相似度计算特征与标记关系矩阵，建立标记关系矩阵，分析标记之间的相关性，进而定义一种二阶策略，获得二阶标记关系组。

2）利用二阶标记关系组，通过增强标记之间的强相关性和削弱标记之间的弱相关性，改进已有的多标记Fisher score，设计基于二阶标记相关性的多标记Fisher score特征选择算法（Multilabel Fisher Score-based feature selection algorithm with second-order Label Correlation， MFSLC），使它初步消除原始不具有分类特性的特征，为后续算法降低时间开销。

3）为了展现多标记数据的边界域中的不确定性，采用多标记分类间隔定义自适应邻域半径及上、下近似集，定义多标记粗糙隶属度函数和多标记模糊邻域粗糙集模型；由此构建模糊邻域熵和多标记模糊邻域熵，在MFSLC基础上，构建基于Fisher score与模糊邻域熵的多标记特征选择算法（MultiLabel Feature Selection algorithm based on Fisher score and fuzzy neighborhood entropy， MLFSF），并给出外部与内部特征重要度的计算公式，使它在预处理的基础上选择最优特征子集。在多标记K近邻（Multilabel K-Nearest Neighbor，MLKNN）分类器下的11个多标记数据集的实验结果验证了本文算法的有效性。

1 基础理论

1.1　Fisher score

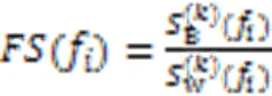
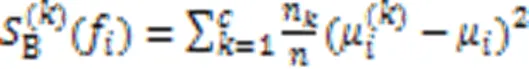
1.2　最大信系数

最大信息系数度量了两个特征变量之间的关联程度，相较于互信息的准确度更高［21］，主要思想是：如果两个变量之间存在一定相关性，那么在这两个变量的散点图上进行某种网格划分之后，根据这两个变量在网格中的近似概率密度分布情况，可以计算这两个变量的互信息。

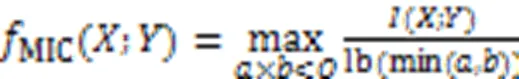
其中：和是在和方向上划分的格子数；是大小为×的网格的上限，依据文献［22］，取样本量的0.6次方效果较好。

1.3　多标记邻域粗糙集

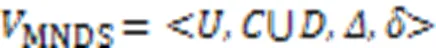
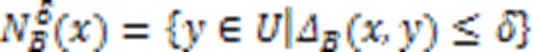
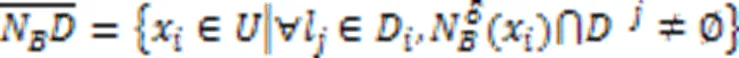
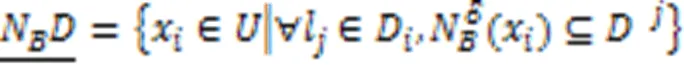
2 多标记特征选择算法

2.1　多标记Fisher score

传统Fisher score未考虑特征与标记以及标记之间的相关性，因此基于二阶标记相关性改进多标记Fisher score。由于在计算标记之间相关性时，现有算法大多从标记空间直接计算得到标记相关性［23］，较少考虑从原始特征空间出发。利用MIC衡量两个变量之间的关联程度。

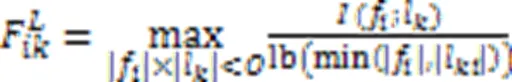
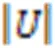
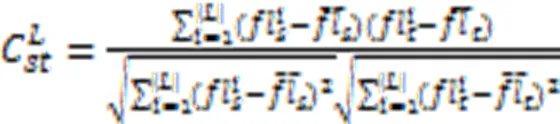
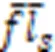
标记之间的二阶策略能够在一定程度上考虑标记之间的相关性，故它的系统泛化性能较优［26］。为了分析标记之间的相关性，基于标记关系矩阵提出一种新的二阶策略。

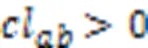
由此得到二阶标记关系组，建立一个多标记论域的划分。

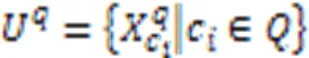
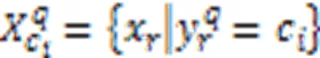
根据定义3得到的二阶标记关系组，具有强相关性和弱相关性的标记组之间具有较大差异。为了使标记间的强弱关系界限能够被明显区分，增强标记之间的强相关性，弱化标记之间的弱相关性，在多标记论域划分的基础上对Fisher score进行改进，使它更适合处理多标记数据。

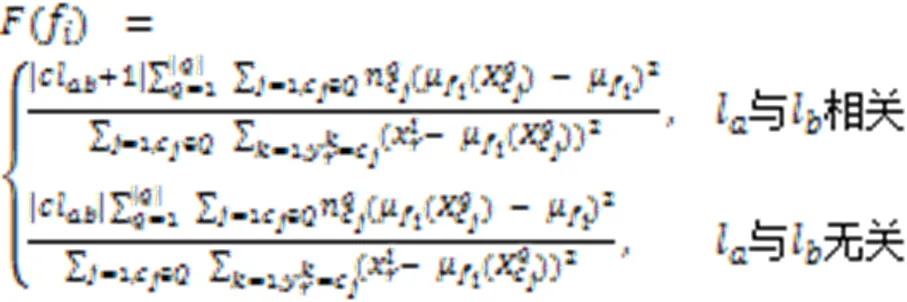
2.2　多标记模糊邻域粗糙集

针对邻域决策系统中邻域半径由手动设置，时间开销大，全局共享同一邻域半径的局限性，使用多标记分类间隔实现邻域半径自适应，不仅可以克服邻域半径手动设置的缺陷，也能解决原始分类间隔过大导致分类无意义的问题。

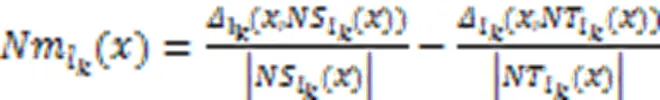
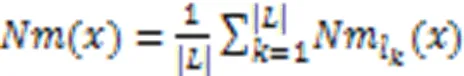
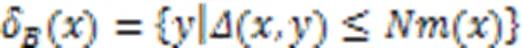
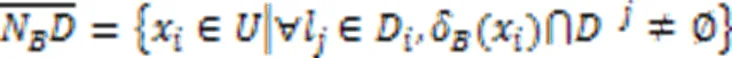
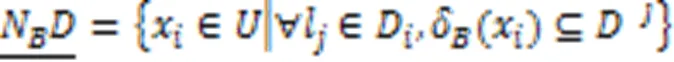
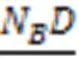
文献［27］中给出了样本与邻域粗糙集之间的隶属关系，通过构造粗糙隶属度函数，将粗糙集转化为模糊集，衡量粗糙集的不确定性。因此，在多标记邻域决策系统中，基于多标记粗糙集构建粗糙集隶属函数，捕捉边界域邻域粒的不确定性，进而定义多标记粗糙隶属度函数。

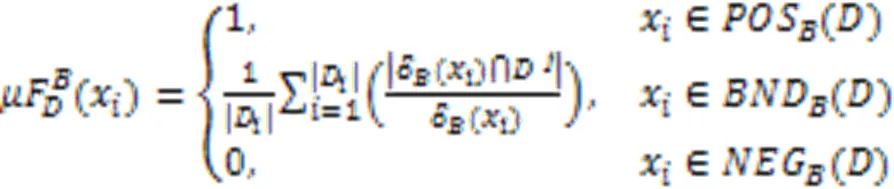
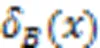
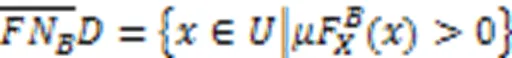
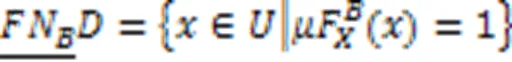
根据每个标记下样本情况，定义11采用普通二分类熵。

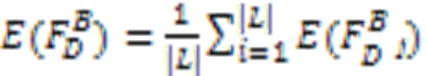
2.3　算法描述

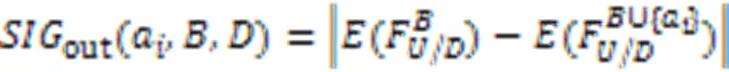
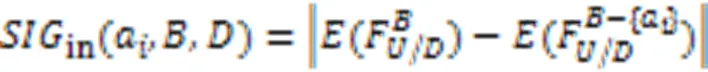
式（22）反映了从当前特征子集中删去特征a后多标记模糊邻域熵的变化程度。在此基础上，借助正向贪心搜索算法迭代地选择具有最大重要度的特征［28］，当加入特征后，不再影响确定性规则生成时，则算法终止。

本文提出基于二阶标记相关性设计多标记Fisher score特征选择算法（MFSLC），如算法1所示。

算法1 MFSLC。

输出候选特征子集。

1）利用式（6）计算特征与标记关系矩阵

2）由式（7）计算标记关系矩阵，根据定义3设计的二阶策略，进而得到多个二阶标记关系组

3）初始化每个特征得分（f）=0

4） For每个二阶标记关系组

5） For每个f∈

6）由式（10）改进Fisher score计算特征f的得分

7） End For

8） End For

9）对每个特征得分进行排序，得到候选特征子集

10） Return候选特征子集

算法2 MLFSF。

输出最优特征子集。

2）使用MFSLC得到初始的候选特征子集

4） For每个x∈

5）根据式（12）与式（13）得到x的邻域半径与邻域类

6） End For

7） For每个特征a∈-

11） End If

14） End For

19） Else返回最优特征子集

20） End If

21） End For

22） Return最优特征子集

在算法2中，假设根据MFSLC得到的候选特征子集个数为，7）～14）计算多标记模糊邻域熵，它的计算复杂度为（）；15）～22）进行多标记模糊邻域熵的特征选择，假设最终约简的特征子集数为，它的计算复杂度为，约为，因此算法2的总计算复杂度为。最终算法1与算法2的总计算复杂度为（2+2lb+）。

2.4　算法异同点

为了加强MLFSF与其他相关算法的异同点的分析讨论，选用5种相关的对比算法：PMU（Pairwise Multi-label Utility algorithm）［30］、MUCO（MUltilabel feature selection algorithm with label COrrelation）［31］、MDDM（Multi-label Dimensionality reduction algorithm via Dependence Maximization）［32］、MFSMR （Multilabel Feature Selection for missing labels using Maximum relevance minimum Redundancy）［19］和基于改进ReliefF的多标记特征选择算法（Multilabel Feature Selection algorithm based on improved ReliefF， MFSR）［33］。表1列出了上述5种对比算法的异同点及计算复杂度。

表1MLFSF与5种对比算法的异同点和计算复杂度

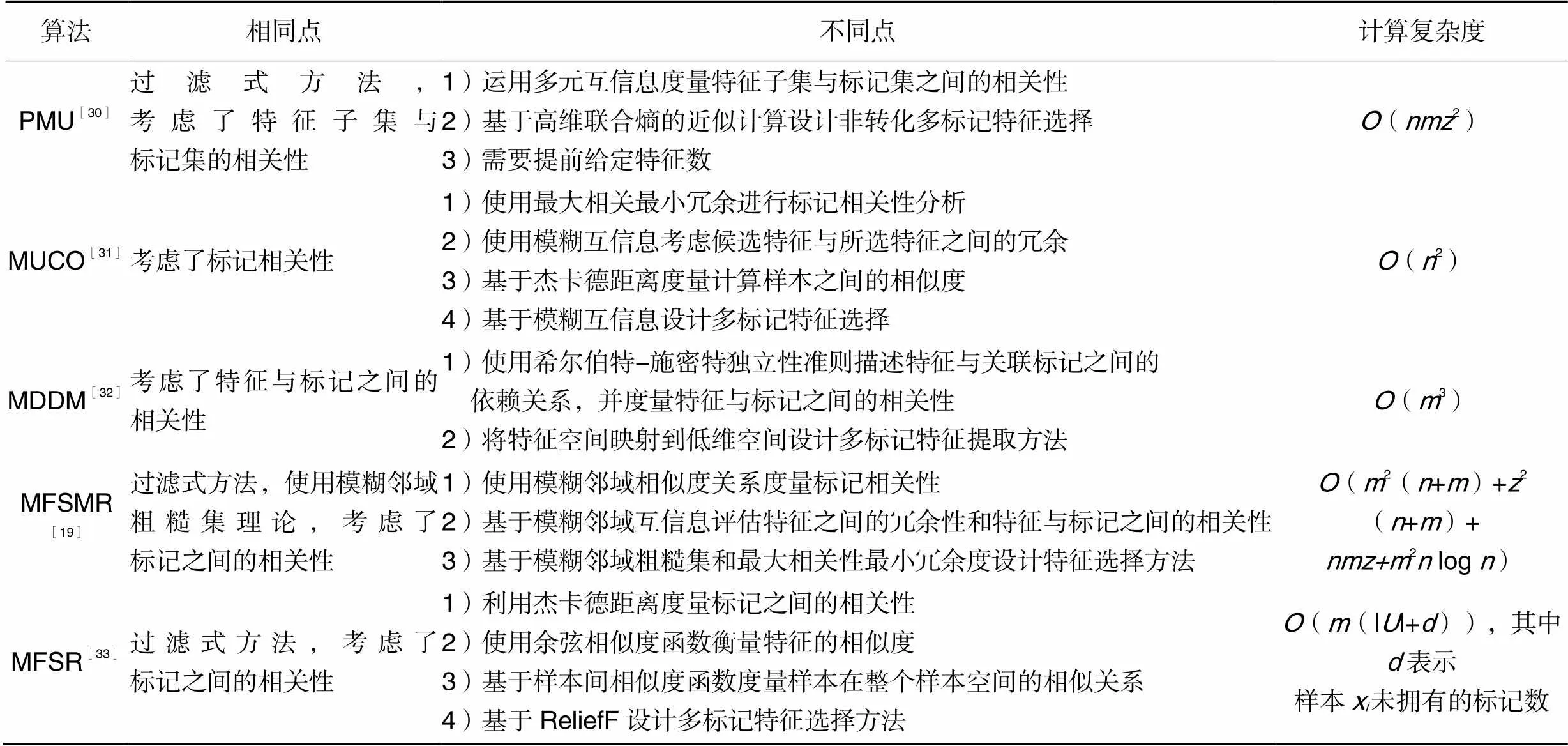
Tab.1　Similarities and differences and computational complexities between MLFSF and five comparative algorithms

3 实验结果与分析

3.1　实验准备

为了测试MLFSF的有效性，从MuLan数据库（http：// mulan.sourceforge.net/datasets.html）中选择了11个多标记数据集，如表2所示。采用MLKNN［3］和5个评价指标：平均分类精度（Average Precision， AP）［34］、汉明损失（Hamming Loss， HL）［35］、排序损失（Ranking Loss， RL）［34］、1-错误率（One Error， OE）［34］、覆盖率（CoVerage， CV）［34］，对算法性能进行分析，并使用选择的特征数（Number of selected Features， FN）展示特征选择的结果。所有实验的硬件环境为64位Windows 7操作系统、内存32 GB、处理器Intel Core i7-7700CPU @ 3.60 GHz，软件为Matlab R2016。

表2多标记数据集的详细信息

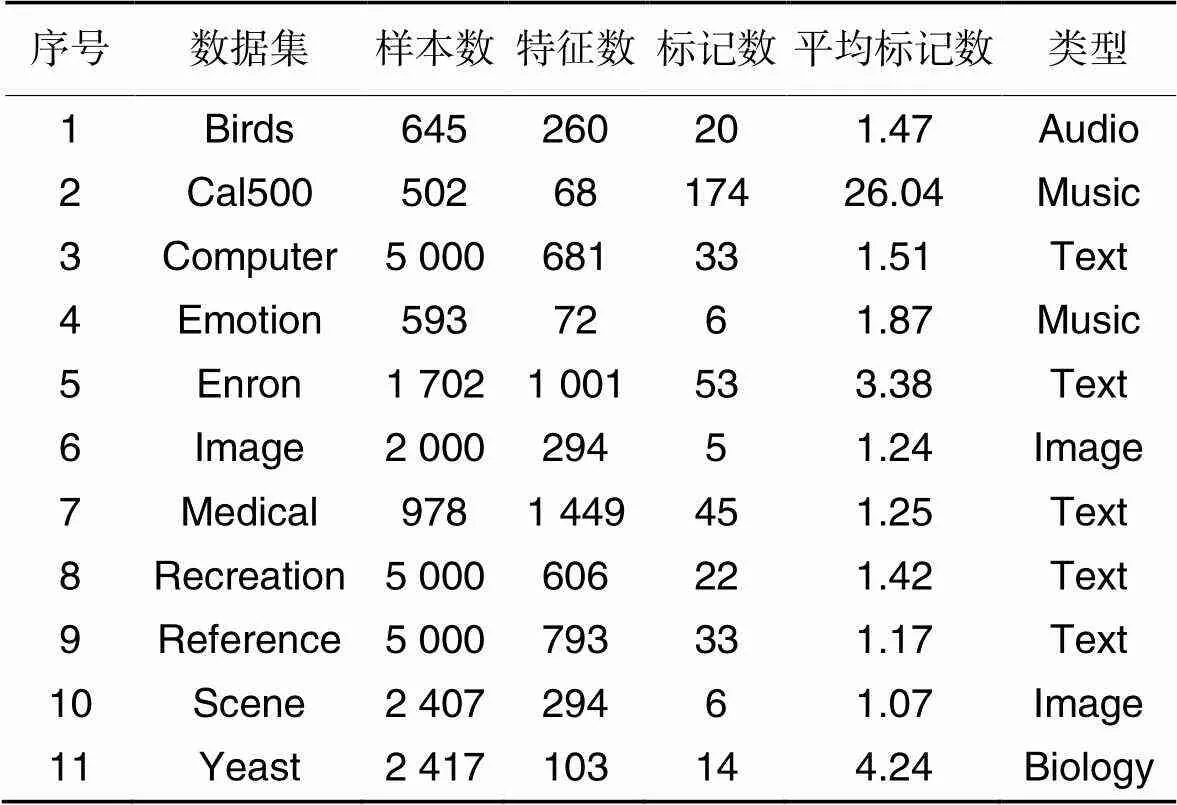
Tab.2　Details of multilabel datasets

3.2　实验结果对比

为了检验算法的有效性，将MLFSF与6种算法进行比较，对比算法主要包括：PMU［30］、MUCO［31］、MDDM-proj［32］、MDDM-spc［32］、MFSMR［19］和MFSR［33］，在11个数据集上通过5个指标评估算法的分类性能。其中对比的4种算法（PMU、MUCO、MDDM-proj和MDDM-spc）的实验数据出自文献［36］。为了保证实验的一致性，实验参数均按照文献［36］，设置MLKNN分类器的平滑参数=1，近邻数=10，并采用五折交叉验证。为了给每个数据集选择合适的FN且更直观地观察指标的变化情况，图1展示了7种算法在11个多标记数据集上的AP指标的变化曲线对比。由于篇幅限制，其余4个指标的变化曲线不再详细叙述。

从图1可知，在Birds、Cal500、Emotion、Enron、Image、Medical、Recreation、Reference、Scene和Yeast这10个数据集上，MLFSF均达到最优。对于Computer数据集，MLFSF整体不如MUCO和PMU，处于中等水平，但指标上升趋势明显，原因可能是忽略了重要特征，导致最终预测的标记数与实际存在差别；对于Emotion数据集，在FN=10和FN>30时，MLFSF高于其他6种算法；对于Enron数据集，在FN<100时，MLFSF整体低于MFSR，当FN>100，MLFSF优于其他6种算法；对于Image数据集，当FN>80时，MLFSF取得了最优值，其余范围均低于MFSMR；对于Recreation数据集，在FN<50时，AP远高于其他6种算法，并取得最优AP，当FN>50时，AP逐渐降低，居于MUCO之下，说明当FN<50时，该部分特征具有重要信息，达到了少而优的目的。因此，结合FN和AP这2种指标的评价结果，在大多数情况下，相较于其他6种算法MLFSF在AP上具有良好的分类效果。

为了更具体地展示MLFSF的分类效果，根据图1以AP指标的最优值指定7种算法在每个数据集上的FN，如表3所示。对表3分析可知，与其他7种算法相比，MLFSF在给定的7个数据集Birds、Computer、Medical、Recreation、Reference、Scene和Yeast上的FN指标均为最优；在剩余4个数据集Cal500、Emotion、Enron和Image上，MLFSF与其他算法差距较小，依次与最优值相差13、13、51和36。对于多标记数据，FN与其余5个指标（AP、HL、RL、OE和CV）在特征选择过程中是同等重要的，因此需要综合考虑各个指标来评价算法的分类性能。表4为8种算法在11个多标记数据集上的5个指标的实验结果，其中，MLKNN表示使用MLKNN分类器对原始多标记数据集进行处理的分类结果。

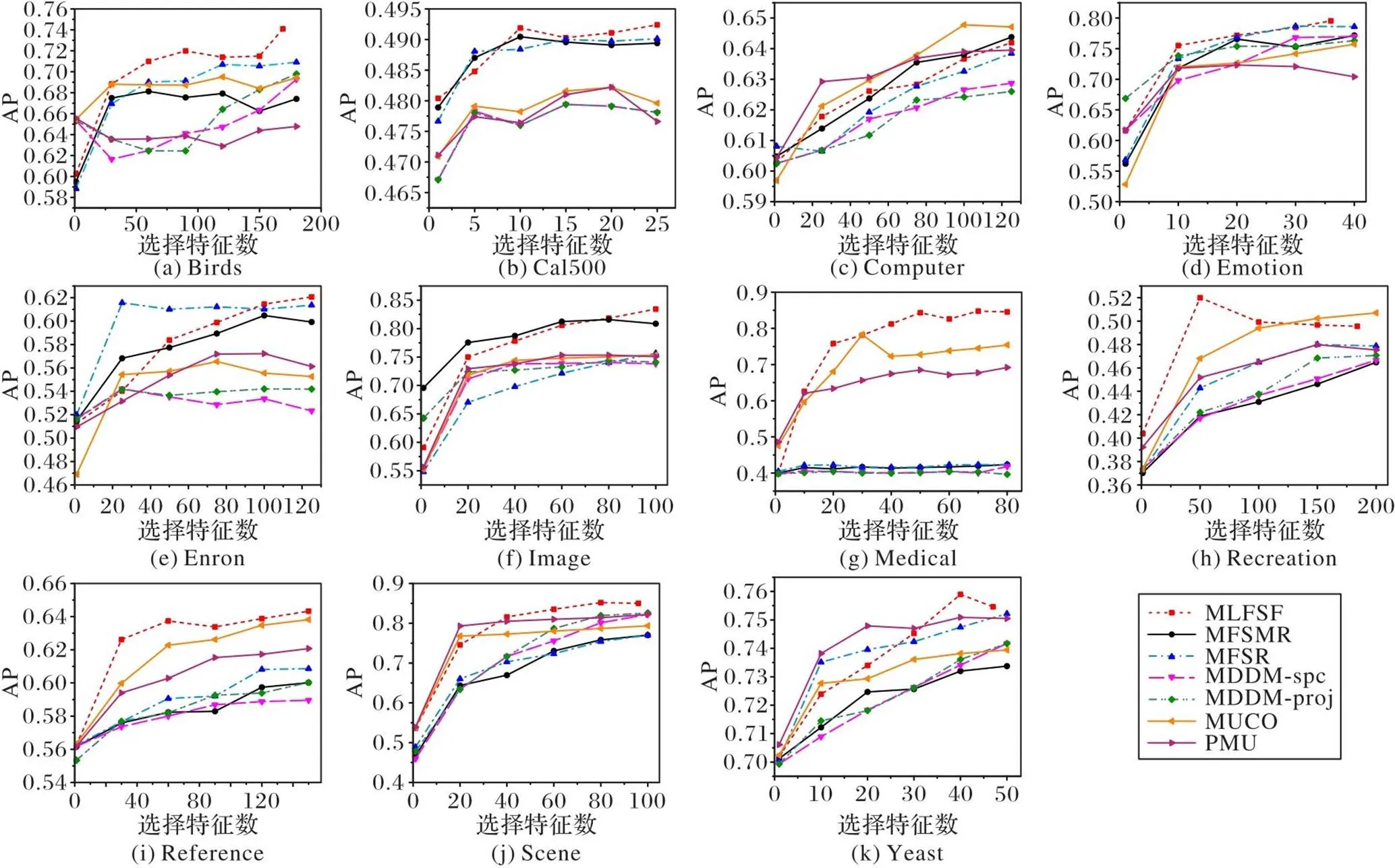
图1　7种算法在11个多标记数据集上的AP（↑）指标比较

表37种算法在11个多标记数据集上的FN（↓）指标比较

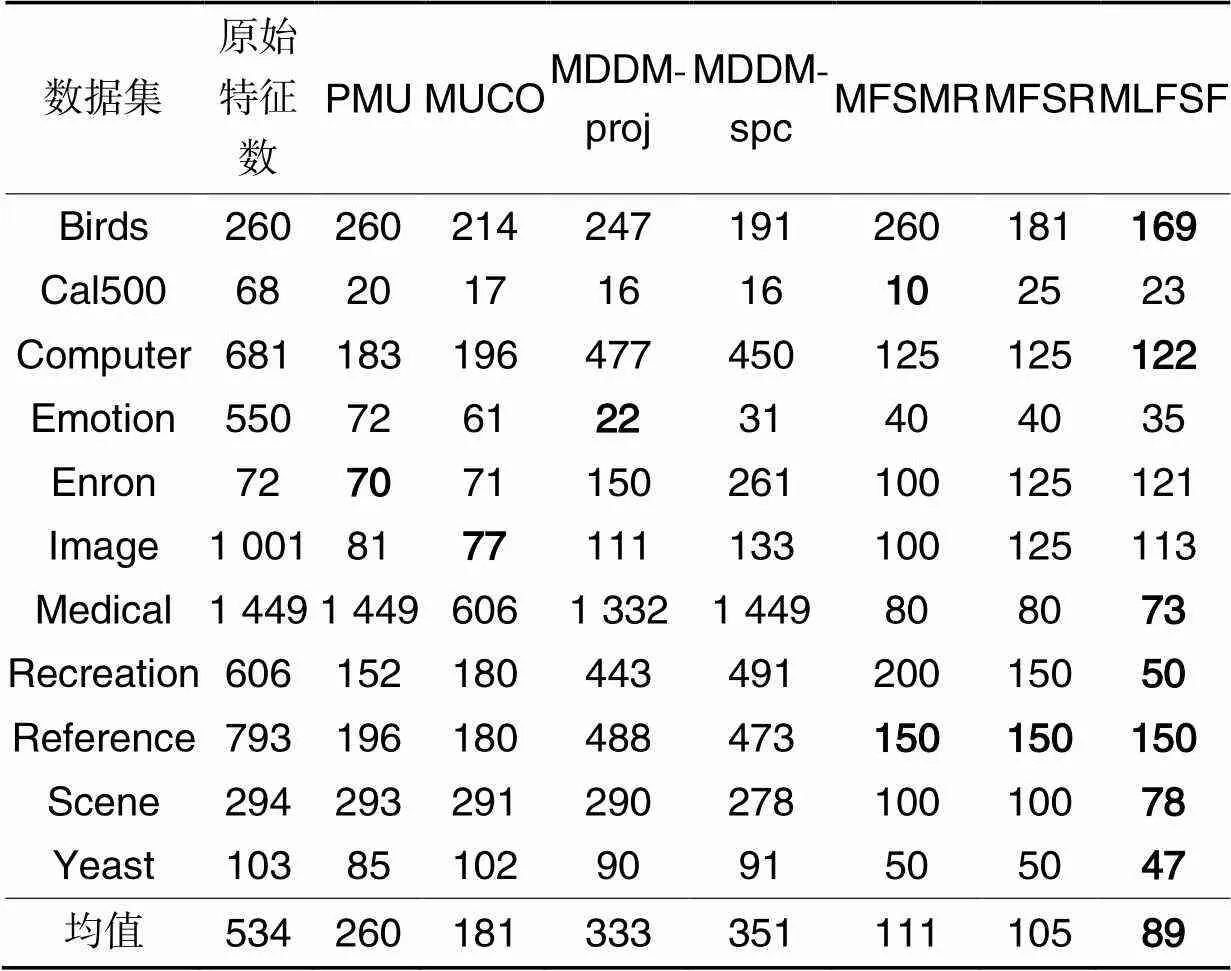
Tab.3　Comparison of seven algorithms on eleven multilabel datasets in terms of FN（↓）

分析表4的实验结果可知，对于AP，与其他7种算法相比，MLFSF在10个数据集Birds、Cal500、Emotion、Enron、Image、Medical、Recreation、Reference、Scene和Yeast上表现最优。其中，在Medical数据集上表现突出，比次优算法MUCO高5.96个百分点，结合表3中的FN，在Medical数据集上的FN也最优；在Computer数据集上，MLFSF的AP高于MLKNN与MFRS，低于其他5种算法，但是根据表3中的FN，MLFSF的FN最少。因此，结合FN和AP这2个指标，MLFSF表现较好。对于HL，与其他7种算法相比，MLFSF在给定的10个数据集Birds、Cal500、Computer、Emotion、Enron、Image、Medical、Recreation、Reference和Scene上表现最优，在Yeast数据集上比最优算法MDDM-spc差0.000 3。其中，在Emotion数据集上，MLFSF比次优MFSR低1.37个百分点，但是它的FN比MFSR更有优势；在Image数据集上，MLFSF与次优算法MFSMR相差1.18个百分点；在Scene数据集上，MLFSF与MDDM-spc均为最优，但对比表3的FN发现，MDDM-spc在FN上没有优势，与MLFSF相差较大。因此，结合FN和HL这2个指标，MLFSF表现较好。对于RL，与其他7种算法相比，MLFSF在给定的10个数据集Birds、Cal500、Emotion、Enron、Image、Medical、Recreation、Reference、Scene和Yeast上均为最优。在Computer数据集上，MLFSF与最优算法MUCO相差0.005 6，但在FN上MLFSF更占优势。其中，在Medical数据集上表现较为显著，与次优算法相差2.05个百分点，且FN为所有算法中最优；在Emotion数据集和Image数据集上，MLFSF分别与次优算法MFSR和MFSMR相差1.36个百分点和1.57个百分点。因此，结合FN和RL这2个指标，MLFSF表现较为良好。对于OE，与其他7种算法相比，MLFSF在给定的8个数据集Birds、Emotion、Enron、Image、Medical、Recreation、Reference和Scene上表现最优；在Cal500数据集上，MLFSF与最优算法MFSR相差0.002 2，但优于其他5种算法；在Computer数据集上，与最优算法MUCO相差0.019 6，优于MFSR、MFSMR与MLKNN；在Reference数据集上，MLFSF与MUCO最优，优于其他6种算法；在Yeast数据集上，MLFSF与最优PMU相差0.002 0，优于其他6种算法，但它在表3中的FN为最小。对于CV指标，与其他7种算法相比，MLFSF在给定的10个数据集Birds、Cal500、Emotion、Enron、Image、Medical、Recreation、Reference、Scene和Yeast上表现最优；在Computer数据集上，MLFSF的CV与最优MUCO相差0.183 0，但是MLFSF在该数据集上的FN最小；在Medical数据集上，比次优MDDM-proj低0.960 0且在该数据集上的FN最小。因此，结合FN指标，MLFSF在CV和OE这2个指标均表现良好。

根据表4的5个指标的整体结果，MLFSF在11个数据集上整体表现最佳且均值最优。其中，在AP的均值上，MLFSF比次优算法MUCO高了2.47个百分点，比最差算法MFRS高了6.66个百分点。具体地，MLFSF在Birds、Emotion、Enron、Image、Medical、Recreation、Reference和Scene这8个数据集上5个指标表现均是最优值，这些数据集是特征空间分布稠密的连续型数据或离散型数值的数据，相较于分布稀疏的特征空间中每一维特征的重要度都小，不易去除特征，而MLFSF中的多标记模糊邻域熵过滤准则能够筛选特征重要度较大特征，更适合特征空间分布稠密的数据集，因此MLFSF在这些数据集上效果表现优异。在Cal500数据集上，MLFSF只在OE指标上未取得最优值，排名第3，但与最优值相差较小，故整体表现良好；在Yeast数据集上，共拥有3个评价指标的最优值AP、RL和CV，上述分析中，在HL和OE指标中与最优值仅有略微差距，但选择特征数最少，所以部分重要的特征未被选中影响了最终的分类性能；在Computer数据集上，只在HL指标上表现最优，其余指标上表现一般，观察发现，在该数据集选择特征数较小，导致重要特征被漏掉，另一方面，在该数据集的特征空间分布上，数值分布较为稀疏，虽然算法考虑特征之间的相关性，但忽略了同等重要的特征也会成为冗余，造成最终结果不佳。总体地，虽然在个别数据集上选择出的特征子集存在冗余信息，但在大部分数据集上MLNIF能够带来较好的分类效果。

表48种算法在11个多标记数据集上的5个评价指标比较

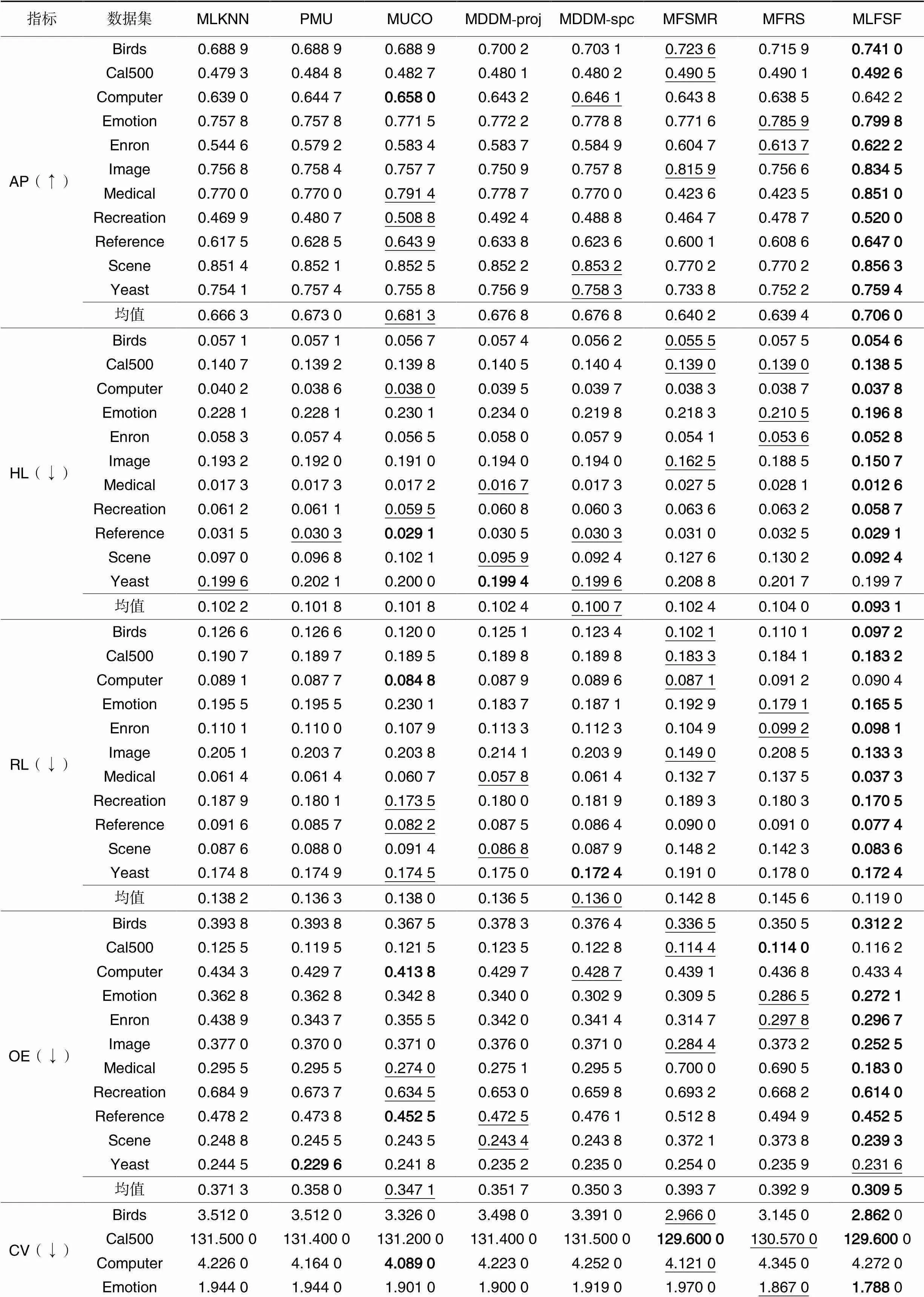
Tab.4　Comparison of eight algorithms on eleven multilabel datasets in terms of five metrics

注：“↑”表示值越大越好，“↓”表示值越小越好；粗体表示最佳结果，下画线表示次优结果。

3.3　统计分析

为了分析所有算法在每个评价指标上的统计性能，采用Friedman测试和Nemenyi测试［4］。Friedman统计量表示如下：

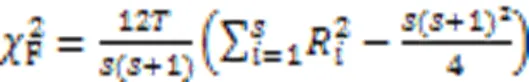
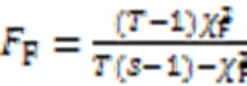
其中：和分别为数据集和算法的数量；R（=1，2，…，）表示第个算法在所有数据集上的平均排序。这里的临界值域（Critical Difference， CD）的计算公式为：

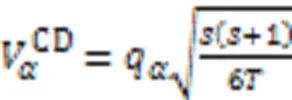
其中：q表示测试的临界列表值，为显著性级别。采用CD图可视化显示所有比较算法之间的差异性［4］。如果两个算法的平均排名差在一个误差之内，则使用连线将它们连接起来；否则在统计学上认为它们之间具有显著差异，其中不同颜色的连线是为了区分不同的两种算法之间存在显著差异［16］。

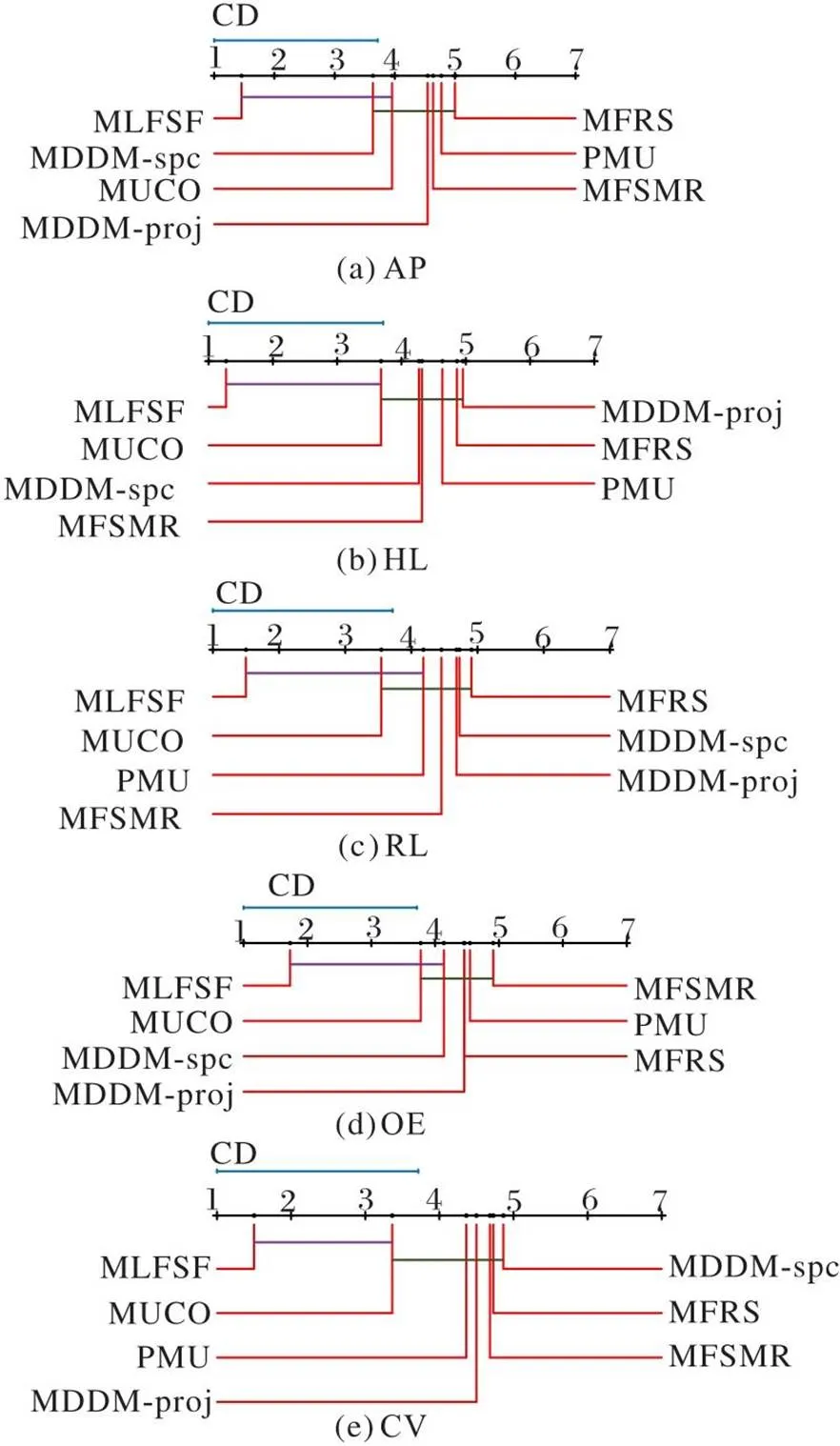
图2　7种算法在5个指标上的Nemenyi检验结果

表57种算法的5个评价指标的统计结果

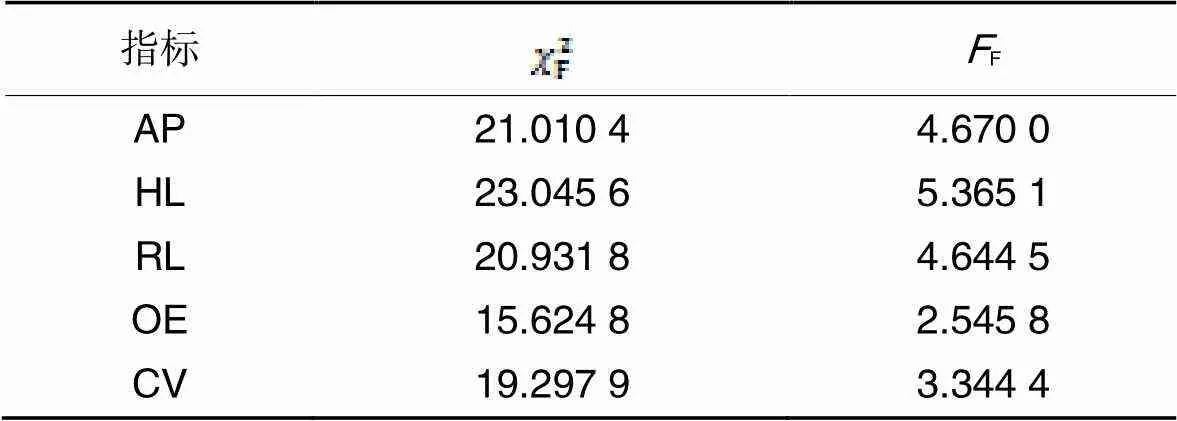
Tab.5　Statistical results of five metrics for seven algorithms

4 结语

现有的多标记Fisher score易忽略特征与标记之间以及标记之间相关性，导致分类性能下降，且使用多标记邻域粗糙集进行约简时会忽略边界域的不确定性信息。为解决上述问题，提出了一种基于Fisher score与模糊邻域熵的多标记特征选择算法。首先，为了衡量标记与特征之间的相关性，通过MIC得到特征与标记关系矩阵，在此基础上使用修正余弦相似度计算特征与标记关系矩阵，进一步得到标记关系矩阵，给出一种标记相关性的二阶策略，从而得到二阶标记关系组；其次，为了增强标记之间的强相关性与削弱标记之间的弱相关性，改进传统Fisher score，从而对多标记数据进行预处理；再次，利用分类间隔得到自适应的邻域半径构建多标记邻域上、下近似集，为了挖掘边界域的知识粒度的不确定性，构造多标记粗糙隶属度函数，得到新的多标记模糊邻域粗糙集模型，提出模糊邻域熵和多标记模糊邻域熵，并给出相应的性质和定理；最后，设计了一种基于Fisher score与模糊邻域熵的多标记特征选择算法。在11个多标记数据集上进行测试，实验结果验证了所提算法是有效的。但是，通过观察实验结果可以看出，对于特征空间分布较稀疏的文本类多标记数据集，MLFSF在MLKNN分类器下的分类效果提升不明显，因而，针对此问题仍需进一步探索和研究。

[1] SUN L， YIN T， DING W， et al. Multilabel feature selection using ML-ReliefF and neighborhood mutual information for multilabel neighborhood decision systems［J］. Information Sciences， 2020， 537： 401-424.

[2] 张志浩，林耀进，卢舜，等. 缺失标记下基于类属属性的多标记特征选择［J］. 计算机应用， 2021， 41（10）： 2849-2857.（ZHANG Z H， LIN Y J， LU S， et al. Multi-label feature selection based on label-specific feature with missing labels［J］. Journal of Computer Applications， 2021， 41（10）： 2849-2857.）

[3] 孙林，黄苗苗，徐久成. 基于邻域粗糙集和Relief的弱标记特征选择方法［J］. 计算机科学， 2022， 49（4）： 152-160.（SUN L， HUANG M M， XU J C. Weak label feature selection method based on neighborhood rough sets and Relief［J］. Computer Science， 2022， 49（4）： 152-160.）

[4] 阮梓航，肖先勇，胡文曦，等. 基于多粒度特征选择和模型融合的复合电能质量扰动分类特征优化［J］. 电力系统保护与控制， 2022， 50（14）： 1-10.（RUAN Z H， XIAO X Y， HU W X， et al. Multiple power quality disturbance classification feature optimization based on multi-granularity feature selection and model fusion ［J］. Power System Protection and Control， 2022， 50（14）： 1-10.）

[5] 滕俊元，高猛，郑小萌，等. 噪声可容忍的软件缺陷预测特征选择方法［J］. 计算机科学， 2021， 48（12）： 131-139.（TENG J Y， GAO M， ZHENG X M， et al. Noise tolerable feature selection method for software defect prediction ［J］. Computer Science， 2021， 48（12）： 131-139.）

[6] SUN L， WANG T， DING W， et al. Feature selection using Fisher score and multilabel neighborhood rough sets for multilabel classification ［J］. Information Sciences， 2021， 578： 887-912.

[7] 汪正凯，沈东升，王晨曦. 基于文本分类的Fisher Score快速多标记特征选择算法［J］. 计算机工程， 2022， 48（2）： 113-124.（WANG Z K， SHEN D S， WANG C X. Fisher Score fast multi-label feature selection algorithm based on text classification［J］. Computer Engineering， 2022， 48（2）： 113-124.）

[8] GUYON I， WESTON J， BARNHILL S， et al. Gene selection for cancer classification using support vector machines［J］. Machine Learning， 2002， 46： 389-422.

[9] GÜNES S， POLAT K， YOSUNKAYA S. Multi-class f-score feature selection approach to classification of obstructive sleep apnea syndrome［J］. Expert Systems with Applications， 2010， 37（2）： 998-1004.

[10] 孙林，黄金旭，徐久成. 基于邻域容差互信息和鲸鱼优化算法的非平衡数据特征选择［J］.计算机应用， 2023， 43（6）： 1842-1854.（SUN L， HUANG J X， XU J C. Feature selection for imbalanced data based on neighborhood tolerance mutual information and whale optimization ［J］. Journal of Computer Applications， 2023， 43（6）： 1842-1854.）

[11] HANCER E， XUE B， ZHANG M. Differential evolution for filter feature selection based on information theory and feature ranking［J］. Knowledge-Based Systems， 2018， 140： 103-119.

[12] 吴迪，郭嗣琮. 改进的Fisher Score特征选择方法及其应用［J］. 辽宁工程技术大学学报（自然科学版）， 2019， 38（5）： 472-479.（WU D， GUO S Z. An improved Fisher Score feature selection method and its application［J］. Journal of Liaoning Technical University （Natural Science）， 2019， 38（5）： 472-479.）

[13] 段洁，胡清华，张灵均，等. 基于邻域粗糙集的多标记分类特征选择算法［J］. 计算机研究与发展， 2015， 52（1）： 56-65.（DUAN J， HU Q H， ZHANG L J， et al. Feature selection for multi-label classification based on neighborhood rough sets［J］. Journal of Computer Research and Development， 2015， 52（1）： 56-65.）

[14] LIN Y， HU Q， LIU J， et al. Multi-label feature selection based on neighborhood mutual information［J］. Applied Software Computation， 2016， 38： 244-256.

[15] LIU J， LIN Y， LI Y ， et al. Online multi-label streaming feature selection based on neighborhood rough set［J］. Pattern Recognition， 2018， 84： 273-287.

[16] HUANG M， SUN L， XU J， et al. Multilabel feature selection using Relief and minimum redundancy maximum relevance based on neighborhood rough sets ［J］. IEEE Access， 2020， 8： 62011-62031.

[17] WU Y， LIU J， YU X， et al. Neighborhood rough set based multi-label feature selection with label correlation［J］. Concurrency and Computation： Practice and Experience， 2022， 34（22）： e7162.

[18] CHEN P， LIN M， LIU J. Multi-label attribute reduction based on variable precision fuzzy neighborhood rough set ［J］. IEEE Access， 2020， 8： 133565-133576.

[19] SUN L， YIN T， DING W， et al. Feature selection with missing labels using multilabel fuzzy neighborhood rough sets and maximum relevance minimum redundancy ［J］. IEEE Transactions on Fuzzy Systems， 2022， 30（5）： 1197-1211.

[20] XU J， SHEN K，SUN L. Multi-label feature selection based on fuzzy neighborhood rough sets ［J］. Complex & Intelligent Systems， 2022， 8： 2105-2129.

[21] 张大斌，张博婷，凌立文，等.基于二次分解聚合策略的我国碳交易价格预测［J］.系统科学与数学， 2022， 42（11）： 3094-3106.（ZHANG D B， ZHANG B T， LING L W， et al. Carbon price forecasting based on secondary decomposition and aggregation strategy［J］. Journal of Systems Science and Mathematical Sciences， 2022， 42（11）： 3094-3106.）

[22] RESHEF D N， RESHEF Y A， FINUCANE H K， et al. Detecting novel associations in large data sets［J］. Science， 2011， 334（6062）： 1518-1524.

[23] 刘琨，封硕. 加强局部搜索能力的人工蜂群算法［J］. 河南师范大学学报（自然科学版）， 2021， 49（2）： 15-24.（LIU K， FENG S. An improved artificial bee colony algorithm for enhancing local search ability［J］. Journal of Henan Normal University （Natural Science Edition）， 2021， 49（2）： 15-24.）

[24] SARWAR B， KARYPIS G， KONSTAN J， et al. Item-based collaborative filtering recommendation algorithms［C］// Proceedings of the 10th International Conference on World Wide Web. New York： ACM， 2001： 285-295.

[25] 黄剑湘，林铮，刘可真，等. 考虑换流站海量事件的关联规则挖掘分析方法［J］. 电力系统保护与控制， 2022， 50（12）： 117-125.（HUANG J X， LIN Z， LIU K Z， et al. Association rule mining analysis method considering massive events in a converter station ［J］. Power System Protection and Control， 2022， 50（12）： 117-125.）

[26] 余鹰. 多标记学习研究综述［J］. 计算机工程与应用， 2015， 51（17）： 20-27.（YU Y. Survey on multi-label learning［J］. Computer Engineering and Applications， 2015， 51（17）： 20-27.）

[27] ZHENG T， ZHU L. Uncertainty measures of neighborhood system based rough sets［J］. Knowledge Based Systems， 2015， 86： 57-65.

[28] 刘艳，程璐，孙林. 基于K-S检验和邻域粗糙集的特征选择方法［J］. 河南师范大学学报（自然科学版）， 2019， 47（2）： 21-28.（LIU Y， CHENG L， SUN L. Feature selection method based on K-S test and neighborhood rough sets［J］. Journal of Henan Normal University （Natural Science Edition）， 2019， 47（2）： 21-28.）

[29] 姚晟，徐风，赵鹏，等. 基于改进邻域粒的模糊熵特征选择算法［J］.南京大学学报（自然科学）， 2017， 53（4）： 802-814.（YAO S， XU F， ZHAO P， et al. Fuzzy entropy feature selection algorithm based on improved neighborhood granule ［J］. Journal of Nanjing University （Natural Science）， 2017， 53（4）： 802-814.）

[30] LEE J， KIM D-W. Feature selection for multi-label classification using multivariate mutual information［J］. Pattern Recognition Letters， 2013， 34（3）： 349-357.

[31] LIN Y， HU Q， LIU J， et al. Streaming feature selection for multilabel learning based on fuzzy mutual information［J］. IEEE Transactions on Fuzzy Systems， 2017， 25（6）： 1491-1507.

[32] ZHANG Y， ZHOU Z-H. Multilabel dimensionality reduction via dependence maximization［J］. ACM Transactions on Knowledge Discovery from Data， 2010， 4（3）： Article No. 14.

[33] 孙林，陈雨生，徐久成. 基于改进ReliefF的多标记特征选择算法［J］. 山东大学学报（理学版）， 2022， 57（4）： 1-11.（SUN L， CHEN Y S， XU J C. Multilabel feature selection algorithm based on improved ReliefF ［J］. Journal of Shandong University （Natural Science）， 2022， 57（4）：1-11.）

[34] SCHAPIRE R E， SINGER Y. BoosTexter： a boosting-based system for text categorization［J］. Machine Learning， 2000， 39： 135-168.

[35] TSOUMAKAS G， VLAHAVAS I. Random-labelsets： an ensemble method for multilabel classification ［C］// Proceedings of the 2007 European Conference on Machine Learning. Berlin： Springer， 2007： 406-417.

[36] CHEN L， CHEN D. Alignment based feature selection for multi-label learning［J］. Neural Processing Letters， 2019， 50： 2323-2344.

Multilabel feature selection algorithm based on Fisher score and fuzzy neighborhood entropy

SUN Lin1*， MA Tianjiao2， XUE Zhan’ao2，3

（1，，300457，；2，，453007，；3（），453007，）

For that Fisher score model does not fully consider feature-label and label-label relations， and some neighborhood rough set models easily neglect the uncertainty of knowledge granulations in the boundary region， resulting in the low classification performance of these algorithms， a MultiLabel feature selection algorithm based on Fisher Score and Fuzzy neighborhood entropy （MLFSF） was proposed. Firstly， by using the Maximum Information Coefficient （MIC） to evaluate the feature-label association degree， the relationship matrix between features and labels was constructed， and the correlation between labels was analyzed by the relationship matrix of labels based on the adjusted cosine similarity. Secondly， a second-order strategy was given to obtain multiple second-order label relationship groups to reclassify the multilabel domain， where the strong correlation between labels was enhanced and the weak correlation between labels was weakened to obtain the score of each feature. The Fisher score model was improved to preprocess the multilabel data. Thirdly， the multilabel classification margin was introduced to define the adaptive neighborhood radius and neighborhood class， and the upper and lower approximation sets were constructed. On this basis， the multilabel rough membership degree function was presented， and the multilabel neighborhood rough set was mapped to the fuzzy set. Based on the multilabel fuzzy neighborhood， the upper and lower approximation sets and the multilabel fuzzy neighborhood rough set model were developed. Thus， the fuzzy neighborhood entropy and the multilabel fuzzy neighborhood entropy were defined to effectively measure the uncertainty of the boundary region. Finally， the Multilabel Fisher Score-based feature selection algorithm with second-order Label Correlation （MFSLC） was designed， and then the MLFSF was constructed. The experimental results applied to 11 multilabel datasets with the Multi-Label K-Nearest Neighbor （MLKNN） classifier show that when compared with six state-of-the-art algorithms including the Multilabel Feature Selection algorithm based on improved ReliefF （MFSR）， MLFSF improves the mean of Average Precision （AP） by 2.47 to 6.66 percentage points； meanwhile， MLFSF obtains optimal values for all five evaluation metrics on most datasets.

multilabel learning; feature selection; Fisher score; multilabel fuzzy neighborhood rough set; fuzzy neighborhood entropy

This work is partially supported by National Natural Science Foundation of China （62076089， 61976082）.

SUN Lin， born in 1979， Ph. D.， professor. His research interests include granular computing， data mining， machine learning.

MA Tianjiao， born in 1998， M. S. candidate. Her research interests include multilabel learning.

XUE Zhan’ao， born in 1963， Ph. D.， professor. His research interests include granular computing， three-way decision.

TP181

1001-9081（2023）12-3779-11

10.11772/j.issn.1001-9081.2022121841

2022⁃12⁃09；

2023⁃01⁃29；

2023⁃01⁃31。

国家自然科学基金资助项目（62076089， 61976082）。