基于滑动四分位和可行搜索圆算法的风速-功率异常数据清洗方法
2024-01-09白星振隋舒婷葛磊蛟朱爱莲顾志成
白星振,隋舒婷,葛磊蛟,朱爱莲,赵 康,顾志成
(1. 山东科技大学 电气与自动化工程学院,山东 青岛 266590;2.国网山东省电力公司 阳谷县供电公司,山东 聊城 252300;3. 天津大学 智能电网教育部重点实验室,天津 300072;4. 青岛龙发热电有限公司,山东 青岛 266317)
风能作为一种环境友好且经济实用的可再生能源,是国家“碳达峰、碳中和”的主力军[1-3]。风电场建成投运后,根据实际运行条件下风速和功率数据得到的风电机组出力曲线不仅能够表征风电机组的实际运行情况,也能够衡量机组的出力水平[4]。良好的风电机组出力曲线对风速和功率数据的质量有很高要求,但受地理条件、运行环境、弃风限电等多因素影响,风电场数据采集与监视控制(supervisory control and data acquisition,SCADA)系统实时采集的风电场运行数据常存在较多的奇异数据,严重影响了风速和功率本应有的整体分布规律和对应关系,无法直接用于风电机组的性能分析和风电场调度管理,因此对采集的风电场运行数据进行识别和清洗[4-5]非常必要。
目前,针对风速-功率异常数据识别和清洗方面,国内外学者进行了一些研究。已有的数据清洗算法主要存在三类问题。一是奇异数据的漏检,如文献[4]采用最优组内方差算法识别异常数据,但仅能识别位于功率曲线下方的堆积型异常数据,且需要大量的迭代计算;文献[5]采用基于密度的局部离群因子算法,能有效识别分散型异常数据,但不能识别成堆出现的异常数据。二是在识别异常数据的同时删除了大量正常运行的数据,不能保证正常运行数据的完整性,如文献[6]采用四分位法和k-means算法剔除异常数据,但没有给出具体的剔除标准,会导致正常运行数据被误删,而且对于不同的弃风数据簇,聚类算法中k值的选取目前没有统一的标准;文献[7]基于Copula理论建立了风电机组的等效置信边界模型,但需要多台风机运行数据,数据需求量大,且数据删除率高,常出现误删。三是清洗效率低下,如文献[8]建立非线性模型判别异常数据,但清洗效率低且对样本数据的需求量大;文献[9]采用四分位法和基于密度的聚类算法确定出越限风功率数据的识别边界,但算法本身存在较多控制参数且数据处理速度较慢。
综上,现有的数据清洗算法主要存在数据删除率高、异常数据漏检、清洗效率低等问题。本研究提出一种基于滑动四分位和可行搜索圆(feasible search circle,FSC)算法的异常数据清洗方法,该方法首先删除原始风速-功率数据中功率小于等于零的数据,然后利用滑动四分位算法清洗掉位于风功率曲线周围的功率散点,最后利用FSC算法完成分布密集的异常数据簇的识别和清洗。实验结果表明,本研究所提的基于滑动四分位和FSC算法的清洗方法能够实现多类型异常数据的识别和清洗,具有运算简单、清洗时间短、数据删除率低的优点。
1 风速-功率历史数据分析
标准风功率曲线是在标准工况下根据风电机组设计参数计算得出[10],较难体现风电机组的实际运行状况。实际风电场运行环境下,风电机组SCADA系统采集到的实际风功率曲线数据主带周围分布着大量的异常数据点,除了由系统误差和随机误差等原因产生的少量散点之外,大多数异常数据点是由机组非正常运行引起的。这些数据点一般不能用于功率曲线建立和机组性能分析,必须进行针对性剔除。异常数据可根据其空间分布特征分为两大类:分散型异常数据和堆积型异常数据[17]。图1为我国北方某个风电机组一年内的实测风速-功率曲线与标准功率曲线对比图,图1中(1)、(2)处为分散型异常数据,(3)、(4)处为堆积型异常数据。剔除上述两大类异常数据点之后,保留的数据主带是机组的常规发电状态数据,能较好地反映风电机组的正常工作范围和出力特性。因此,本研究的目的是实现异常数据的有效清洗。
2 异常数据的识别和分析
异常数据产生的原因及其在风功率曲线中存在的形式多样,目前尚无一个算法实现多类型异常数据的完全识别和清洗,因此本研究根据异常数据的空间分布特点,采用滑动四分位算法处理分散型异常数据,采用FSC算法处理堆积型异常数据。
2.1 滑动四分位法
四分位算法[9]通常用于处理分散型异常数据,该算法需要提前进行数据分区且受异常数据量的影响较大,一般不能单独使用。本研究采用的滑动四分位法将滑动窗口[11]与四分位法结合。设原始数据集为:
W={(v1,p1),(v2,p2),…,(vn,pn)}。
(1)
式中:vi和pi分别表示第i个数据样本的风速和功率值,数据按照功率升序排列,即pi 1) 计算样本的第2分位数即中位数Q2。 (2) 2) 计算第1、3个分位数Q1和Q3。Q2将v分为两部分(Q2不包含在两部分数据之内),分别计算两部分的中位数Q1、Q3。当L=4k+3(k=0,1,2,…)时,有 (3) 当L=4k+1(k=0,1,2,…)时,有 (4) 3) 计算第1分位数Q1和第3分位数Q3之间的差值IQR,称作四分位距。 IQR=Q3-Q1。 (5) 根据四分位距确定样本中数据的正常值范围为[Q1-1.5IQR,Q3+1.5IQR],位于此范围之外的数据称为异常值。 滑动四分位算法中不同的L和m取值对应着不同的数据处理精度,通过窗口宽度和步长的设置,可以保证一次处理的数据量,灵活改变算法的精度,可较好地实现风功率曲线分散型异常数据点的剔除。 经过滑动四分位算法初步识别之后,大部分位于风功率曲线周围的无规律散点被清除,但位于曲线中部的横向堆积型异常数据仍存在,该类数据多是由弃风限电等原因引起,对于此类异常数据,本研究提出可行搜索圆数据清洗算法。 弃风限电是指因当地电网接纳能力不足、风电不稳定等原因造成的部分风机被迫降低出力或暂停出力的现象,弃风限电产生的原因是多方面的[12-14]。当风电场发生弃风限电时,风电机组的输出功率将不再与风速呈对应关系,而是被限制在一定范围内。此时,在同一风速范围内,正常运行时的功率和发生弃风时的功率相差较大,所以通过弃风数据点偏离正常数据点的程度进行识别,故提出FSC算法。考虑到正常运行数据存在一定的波动范围,发展轨迹不是单一的,故选用欧氏距离作为评判标准,以搜索圆的半径阈值作为搜索的边界值,搜索圆的圆心和半径确定后,可在搜索圆的范围内对正常数据进行全方位搜索,极大减少了漏判和误判率。设经过四分位算法初步处理之后的数据样本集合为: (6) 设置一个长度为2的可变数据窗口[(a1,b1),(a2,b2)],将数据集的第一个数据点(风速数值最小的)看作正常数据点,并将其作为窗口的左端点,即: (7) 将数据集的下一个数据点放在该数据窗口内,以窗口的左端点为圆心,阈值δ为半径作圆,判断数据集的下一个数据点是否在此圆包含的范围内。若在,则该数据点属于当前的数据窗口,为正常数据点,此时将窗口的左端点取出,用该点作为窗口的新的左端点判断下一个数据点;若不在,则该点距离正常数据点较远,视作异常数据点舍弃,继续判断接下来的数据点。 FSC算法示意图如图2所示,si、sj、sl分别是相邻的3个数据点。假设si为正常点,则si∈D,D是长度为2的数据窗口,检验sj时,以si为圆心,δ为半径作圆,比较si和sj之间的欧氏距离d1和δ之间的大小关系: (8) 图2 算法示意图 (9) 进而判断sj可加入窗口。此时,将si取出,用sj作为窗口的左端点,判断接下来的数据点sl。此时,比较数据点sj和sl之间的欧氏距离d2和δ之间的大小关系, (10) 由图2可知,sl不可加入窗口,即sj不是弃风数据点,此时将sl舍去,继续用sj判断下一个数据点。 分析风电机组的实际运行情况发现,原始的风功率曲线中位于曲线中部的横向堆积型异常数据十分常见,若直接在竖直方向(沿着风速变化的方向)使用滑动四分位算法进行数据清洗,四分位算法的内限会受到堆积型异常数据的严重影响,不仅无法正确识别异常数据,还会产生一系列新的异常数据点,影响总体的数据识别效果,不利于后续FSC算法半径阈值的选取,而在水平方向(沿着功率变化的方向)使用滑动四分位算法可避免此类问题。滑动四分位和FSC算法的具体步骤如下: 1) 数据预处理。将原始数据中风速位于切入风速和切出风速之间而功率小于等于零的数据点清除,此类数据在风功率曲线中表现为位于曲线底部的横向密集数据带,如图1中的(4)处所示; 2) 在水平方向运用滑动四分位算法消除分散型异常数据。根据曲线周围分散型异常数据的分布情况,定义合适宽度和步长的滑动窗口(选取方法见2.4节),对每个窗口中的数据采用四分位算法进行识别清洗,可消除功率曲线中的大部分分散型异常数据,避免了数据散点对后续堆积型异常数据的清洗产生干扰,方便FSC算法半径阈值的确定; 3) 对经过滑动四分位算法处理之后的数据用FSC算法进行二次处理,将数据按照风速升序顺序排列,将第一个数据点作为初始圆的圆心,依次沿着风速增大的方向进行异常点搜索,直至遍历完所有数据点,即可得出正常数据集。 滑动四分位和FSC算法流程如图3所示。 图3 滑动四分位和FSC算法流程图 2.4.1 宽度和步长的选取 滑动四分位算法的滑动窗口区间的宽度和步长的阈值的选取参照式(11): (11) 式中:Num为功率数据的总数,L和m需为整数,将风功率数据进行N等分。 2.4.2 半径阈值的选取 良好的半径阈值应能较完整地识别堆积型异常数据,半径阈值的选取依赖于堆积型异常数据区间集合,堆积型异常数据区间的选取参考文献[6],FSC算法半径阈值的选取流程如下。 1) 确定阈值所在的区间[a,c]。求得堆积型异常数据区间集合为Z={U1,U2,…,Um},其中Um={(v1,p1),(v2,p2),…,(vn,pn)},且满足vi 2) 求区间[a,c]的中点b,判断当阈值为b时,经FSC算法处理之后的数据是否含有堆积型异常数据。若含有堆积型异常数据,则半径阈值的最佳取值位于区间[a,b],若处理之后的数据不含有堆积型异常数据,则半径阈值的最佳取值位于区间[b,c]。 3) 继续在区间内进行二分搜索,直到找出最佳的半径阈值,该阈值能基本实现堆积型异常数据的清洗。 以北方某风电场风电机组数据为例,对采用滑动四分位清洗过后的风速-功率数据进行堆积型异常数据区间的判断,确定半径阈值过程如图4所示。 1) 半径阈值的初始范围为[200, 600],当半径阈值为600时,FSC算法的处理效果如图4(a)所示,图中(1)处仍显示异常数据簇,显然不满足清洗要求。 2) 计算初始区间的中点为400,当半径阈值为400时,FSC算法的清洗效果如图4(b)所示,仍有部分堆积型异常数据清洗不彻底,故可知最佳半径阈值应位于区间[200, 400]。 3) 计算区间[200,400]的中点为300,当半径阈值为300时,FSC算法的清洗效果如图4(c)所示,仍存在少量异常数据点,故可知最佳半径阈值位于区间[200, 300]。 4) 依次类推,重复上述步骤,最终取整数确定半径阈值为230时,处理效果如图4(d)所示,处理效果最为合适。 为了更好地说明本研究提出的半径阈值确定方法的数据识别效果,对清洗过后的风功率数据采用bin算法[15]建模,以均方根误差(root mean square error,RMSE)和平均绝对误差(mean absolute error,MAE)作为评价指标,对比不同半径阈值的建模误差大小[16]。其中,每个bin区间的风速和功率均值分别为: (12) (13) 均方根误差RMSE和平均绝对误差MAE的计算式分别为: (14) (15) 表1 风电机组等值功率曲线的评价指标值 结合表1和图4可知,当半径阈值选择为230时,通过bin算法建模得到的风功率曲线最接近于标准的风功率曲线,且建模的RMSE和MAE取得最小值。同时,比较图4(c)和图4(d)可知,只有少量异常数据点存在时,对功率曲线的建模影响很小,故为了方便计算,选取半径阈值时可取近似。 为了说明本研究所提算法和流程的有效性,选取我国北方某风电机组的实际运行数据进行实验验证,取该风电机组2014年9月—2015年8月、2015年9月—2016年8月、2016年9月—2017年8月共3年的原始数据,数据每10 min记录一个点。该风电机组的基本参数为:切入风速为3 m/s,切出风速为23 m/s,额定功率为1 500 kW,额定风速为12 m/s。该风电机组3年间每连续12个月的原始数据如图5所示。 图5 实测风速-功率散点图 由图5可知,该风电场的风电机组3年来的风功率实测数据中存在不同类型的异常数据,但具体分布位置和数量有明显差别。其中,图5(a)中风功率实测数据中两类异常数据均比较典型,图5(b)中风功率实测数据中主要为分散型异常数据,图5(c)中风功率实测数据中主要为堆积型异常数据。 对图5(a)、5(b)、5(c)风电机组的风速-功率实测数据运用滑动四分位算法进行预处理,窗口宽度、步长分别取为40、40,41、41,20、20,初步处理效果如图6所示。 图6 风功率数据初步处理效果图 由图6可知,原始数据经过滑动四分位算法首次处理之后,分散型异常数据基本被剔除,但位于曲线中部横向分布的堆积型异常数据并未被识别,接下来用FSC算法进行下一步处理。按照2.4节所述最佳阈值的选取规则,将半径阈值分别设置为230、200、120,清洗结果与原始数据对比如图7所示。由图7可知,本研究提出FSC算法能够进一步完成堆积型异常数据的清洗。 图7 FSC算法数据清洗效果图 采用本研究所提算法与Thompson tau-四分位算法[17]、LOF算法[18]分别对该风电机组前述数据进行分析,比较3种算法在清洗效果、数据删除率、清洗时间等方面的差距。对比分析时,Thompson tau-四分位算法的舍弃水平设置为0.01;为便于比较,LOF算法的邻域点的个数为20,且LOF算法的数据删除率设置为与本研究算法相同。表2统计了3种方法对该机组3年内的数据删除率、清洗效率情况,Thompson tau-四分位算法、LOF算法的数据清洗效果分别如图8、图9所示。 表2 不同方法的数据清洗效果 图8 Thompson tau-四分位算法清洗效果 图9 LOF算法清洗效果 由表2可知,3种算法的数据删除率、算法效率存在较大差距,具体表现为: 1) 数据删除率。用本研究算法对2014年9月—2016年8月数据进行处理,数据删除率分别为7.24%和9.59%,而采用Thompson tau-四分位算法处理,数据删除量分别为21.49%和21.06%,表明Thompson tau-四分位算法在处理这两年的数据时存在过识别现象,一部分正常数据被误删。结合图7(c)和图8(c)可知,Thompson tau-四分位算法无法准确识别2016年9月—2017年8月的堆积型异常数据。 2) 算法效率。本研究算法对该风电机组3年的数据清洗时间均在5 s左右,Thompson tau-四分位算法的清洗时间约为2~3 min,LOF的清洗时间约为30 s,表明本研究算法效率比Thompson tau-四分位算法和LOF算法均有很大提升。 此外,对比图7、图8可知,Thompson tau-四分位算法可以处理分散型异常数据,但当堆积型异常数据过多时,该算法将失去使用价值。 由表2和图7、图9可知,LOF算法和本研究算法在异常数据识别率相同的情况下,LOF算法对于该风电机组2014年9月—2015年8月实测风功率数据中存在的分散型异常数据处理效果尚可,但基本无法识别该风电机组产生的堆积型异常数据。该风电机组2015年9月—2016年8月产生的异常数据多为分散型异常数据,故LOF算法基本能保留完整的数据主带,但对于以堆积型异常数据为主的2015年9月—2016年8月实测风功率数据处理效果欠佳。 本研究分析了风电机组风速-功率异常数据的来源及分布特征,提出基于滑动四分位和FSC算法的风速-功率异常数据清洗方法,首先采用滑动四分位算法实现了数据散点的清洗,然后针对滑动四分位算法不能有效清洗的横向堆积型异常数据提出了FSC算法。验证结果表明,本研究提出的基于滑动四分位和FSC算法的风速-功率异常数据清洗方法,通过设置算法半径阈值,能够很好地识别并清洗风电机组产生的异常数据,清洗效果不受堆积型异常数据的影响。同时,该方法考虑了风功率数据的运行主带,在实现异常数据清洗的同时尽可能地保留了正常运行的数据点,清洗效率较高,具有一定的实际应用价值。2.2 可行搜索圆法
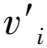

2.3 滑动四分位和FSC算法清洗流程
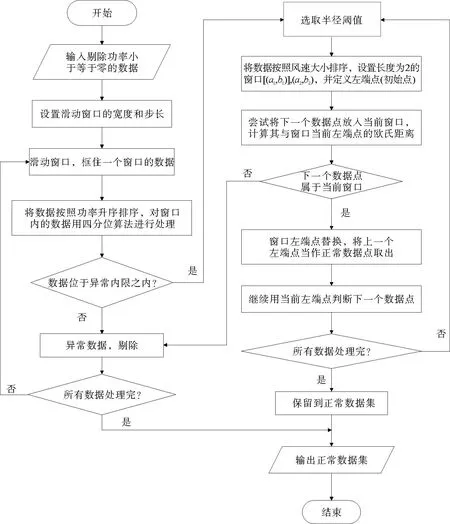
2.4 阈值的选取

3 实验结果与分析
3.1 数据来源
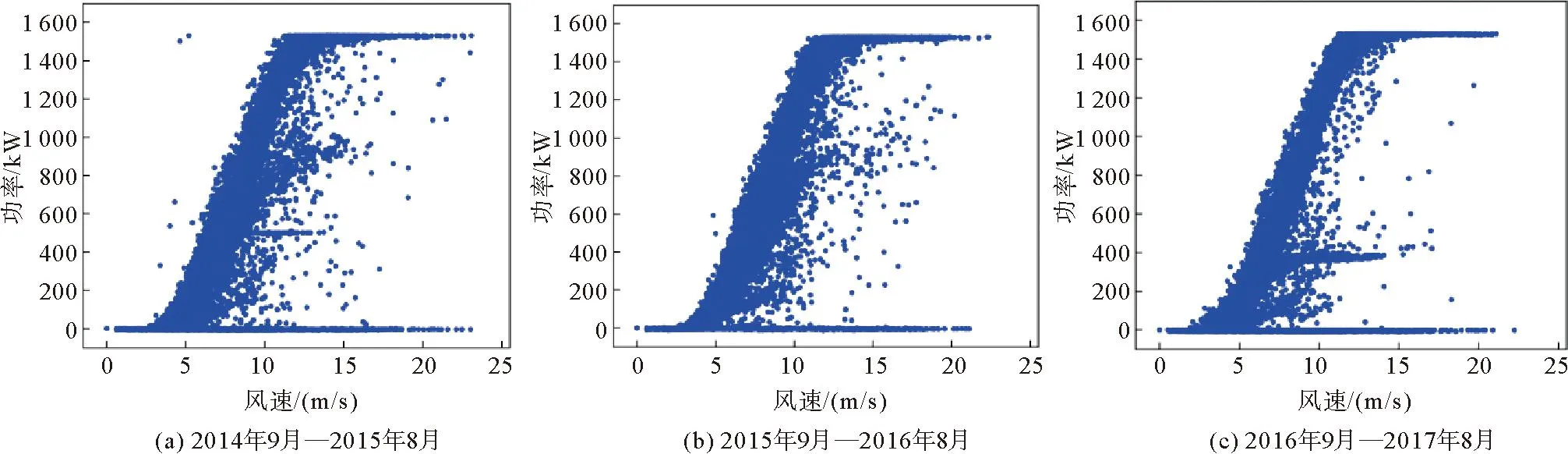
3.2 数据清洗测试


3.3 算法对比分析


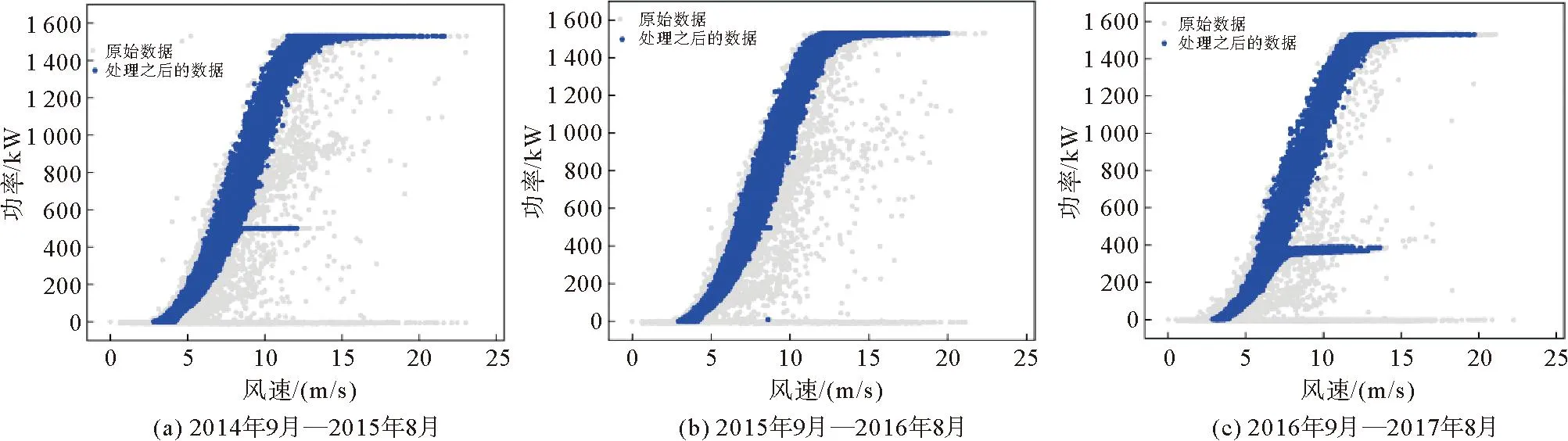
4 结论
