基于混合双层自组织径向基函数神经网络的优化学习算法

杨彦霞, 王 普, 高学金, 高慧慧, 齐泽洋

(1.北京工业大学信息学部, 北京 100124; 2.北京工业大学计算智能与智能系统北京市重点实验室, 北京 100124)

神经网络技术具有大规模并行处理能力、自适应能力和高灵活性等优点,已成为机器学习和数据处理中非常受欢迎的工具。3层的径向基函数神经网络(radial basis function neural network, RBFNN)和反向传播(back propagation, BP)学习算法可以用足够多的神经元逼近任意非线性连续函数且达到任意精度,在现实任务中得到了广泛的应用[1-2]。在使用RBFNN模型来处理实际问题时,该模型通常包括选择合适的网络模型结构以及高效的学习算法[3]。

RBFNN的结构可由网络层数、每层神经元个数、网络的所有连接以及神经元的传递函数表示。众所周知,RBFNN的性能对神经元的数量极其敏感,神经元数量过少会降低网络的逼近能力,而神经元数量过多又可能导致过拟合, 因此,实现更好的网络性能和简化网络结构相互矛盾。多年实践证明,RBFNN结构的训练是一项具有挑战性的任务,而学习算法是RBFNN的核心。常用的学习算法是基于导数的优化算法[4-6],如梯度下降 (gradient descent, GD) 方法、随机梯度下降(stochastic gradient descent, SGD)方法、共轭梯度(conjugate gradient, CG)方法等。列文伯格-马夸尔特(Levenberg Marquardt, LM)算法作为介于牛顿法与GD方法之间的一种非线性优化方法[7-8],对过参数化问题不敏感,并能有效处理冗余参数问题,使代价函数陷入局部极小值的机会大大减小,在计算机视觉、分类、控制等领域得到了广泛应用。 RBFNN的学习过程是基于实际输出和期望输出之间的直接比较,通过迭代调整连接权值实现的,这种学习过程属于监督学习。其中,一种最常用的算法是基于GD的BP算法,即通过迭代调整权值,使误差最小化。

迄今为止,传统的RBFNN学习模型包括单目标优化模型和多目标优化模型。单目标优化模型是RBFNN训练中最常用、研究最广泛的模型,它只包含一个基于网络误差的目标。当网络结构固定时,RBFNN的权值只能通过训练算法进行优化,目标是使网络误差最小化[9-11]。当同时优化网络结构和连接权值时,目标是使网络误差最小或网络误差和网络复杂度的组合最小[12-13]。 需要注意的是,多目标优化模型通常包含2个相互矛盾的目标,即最小化网络误差和最小化隐藏单元数[14-15],并且多目标模型的目的是实现精度和网络结构之间的最优权衡。Goh等[16]设计了一个多目标问题,同时,考虑了分类准确性和网络复杂性这2个相互冲突的目标。 在文献[17]中,Almeida等构造了基于训练误差、结构复杂度和传递函数复杂度的双目标优化问题。其中:一个目标是测试误差、训练误差、隐藏层的数量、隐藏节点的数量、传递函数权重5项信息的组合;另一个目标是基于网络误差的测量。 Loghmanian等[18]同样提出了多目标策略,即最小化均方误差和由输入神经元个数、输出神经元个数、隐藏层神经个数组成的网络复杂度。神经网络训练的另一个常见困难是神经网络中的非线性激活函数使模型收敛到局部最优解而不是全局最优解,模型性能不能达到最优。为解决此问题,提高训练效果,近几十年来多位学者做了大量的工作,例如,将激活函数更改为线性函数,并保持输入和输出的方差近似,利用Xavier初始化网络权值[19]。然而,这类解决方案高度依赖于数据集的数据分布。之后,也有学者提出更改网络结构,即非常著名的长短时记忆(long short term memory, LSTM) 神经网络,通过使用多门结构控制状态存储器的流量,有效解决梯度消失[20-21]问题。将激活函数更改为整流线性单元(rectified linear unit, ReLU)函数也有助于解决消失的梯度问题[22-23],然而当输入为负数时,神经元呈死亡状态。简而言之,输出要么为0,要么为正,这极大限制了其实际应用。

1 问题描述

现有学习模型大都采用先通过训练模型架构和参数得到最优神经网络模型,再测试网络性能的思路。此种机制将训练过程和测试过程分裂成彼此独立的个体,前者不知后者,而后者亦看不到前者,在实际应用时,由此种机制导致的过拟合和欠拟合很难平衡。当一个模型开始记忆训练数据并以突触权重的形式存储知识,而不是从中学习归纳趋势或规则时,极易引起过拟合或欠拟合问题,从而导致泛化性能较差。

为了设计一种紧凑且具有良好泛化能力的RBFNN体系结构,本文构建了一种以网络结构为领导者、以连接权值为跟随者的双层进化学习模型,即基于混合双层自组织径向基函数神经网络的优化学习(hybrid bilevel self-organizing radial basis function neural network optimization learning,Hb-SRBFNN-OL)算法。该方法是一个线性叠加多层神经网络的双层进化学习系统,包括与网络复杂度和测试误差相关的上层结构优化部分,以及与训练误差相关的下层参数优化部分。其优势如下:

1) 不同于以往只使用元启发式算法来优化RBFNN的结构和权值,该算法兼顾了训练误差和测试误差。上层优化器用于优化网络架构,减少测试误差,下层优化器通过最小化训练误差优化给定的RBFNN权重。

2) 通过一个全局损失函数绕过消失梯度问题和减少非凸优化的负面影响,在训练速度和准确性方面提高模型性能。

3) 将测试过程结果反馈给训练过程,通过持续交互、进化学习,有效解决了过拟合和欠拟合问题。

2 Hb-SRBFNN-OL算法

2.1 混合双层优化学习模型结构

为有效平衡神经网络训练中的过拟合和欠拟合,提出一种组合多层神经网络学习框架,如图1所示。

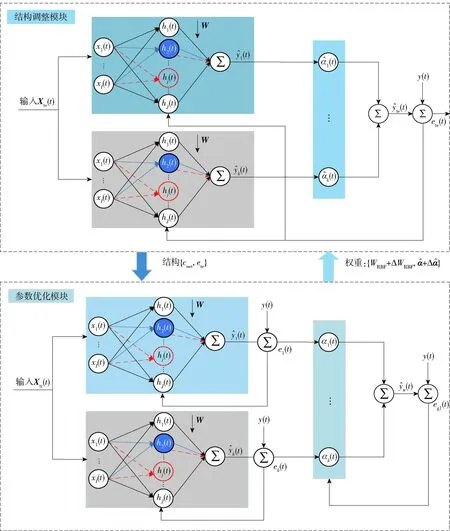
图1 Hb-SRBFNN-OL框架

结构调整模块表示上层优化器,基于测试误差和网络复杂度优化网络结构;参数优化模块表示下层优化器,基于训练误差优化网络权值。Xte和Xtr分别表示测试输入和训练输入数据,te和tr分别为它们对应的预测输出。RBFNN子网络具有相同的结构、不同的初始权值。

参数优化模块,即传统的权值学习算法通过BP输出误差el,k(t)=k(t)-yk(t)更新第k个子网络中的所有参数,使预测输出k(t)在t→∞时逐渐接近其真标签yk(t)。

(1)

(2)

φj(t)=e-‖X(t)-Cj(t)‖2/(2σj(t)2)

(3)

式中:wj(t)为t时刻第j个隐藏层神经元与输出之间的权重;φj(t)为第j个隐藏层神经元在t时刻的输出;Cj(t)=[cj1(t),cj2(t),…,cjI(t);j=1,2,…,J]为第j个隐藏层神经元在t时刻的中心向量;X(t)=[x1(t),x2(t), …,xI(t)]T为RBFNN在t时刻的I维输入向量;‖·-·‖ 表示欧氏距离;σj(t)为第j个隐藏层神经元在t时刻的宽度;i(t)为第i个子网络在时间步t的组合系数, 目标系数αi(t)满足准则

(4)

在任意时刻,当前系数的估计值满足

(5)

2.2 上层目标:网络结构优化

对于一个典型的3层RBFNN,输入神经元的个数和输出神经元的个数分别取决于训练模式和训练样本,而核心问题在于优化过程获得最优数量的隐藏层神经元个数。因此,一个3层的多输入单输出RBFNN结构可以表示为I-J-1。I表示输入维度,J表示隐藏层神经元个数。 假设最大隐藏层神经元数量为Jmax,隐藏层结构表示为h=[h1,h2,…,hJmax],hJmax表示第Jmax个隐藏层神经元的状态。

自组织RBFNN(self-organizing RBFNN,SO-RBFNN)的拓扑结构见图2。对于保留神经元,它与输入层的每个神经元和输出层的每个神经元都有连接。蓝色神经元表示新添加神经元,而红色虚线神经元为删除神经元,即断开网络中该神经元的所有连接。网络结构的自适应调整过程即本文所提模型框架的上层网络优化过程。

上层目标主要考虑2个指标:网络复杂度cnet和测试误差ete,并分别优化这2个指标。基于此,对网络结构进行自适应调整,目的是获得紧凑且泛化能力良好的RBFNN结构。上层目标函数定义为

Lu=c1×cnet+c2×ete

(6)

式中:c1,c2∈(0,1)表示权重系数;cnet用来描述网络拓扑结构。网络复杂度的值越小,说明网络越简单、越紧凑。cnet定义为

(7)

式中:Ac表示上层SO-RBFNN得到的实际网络连接数;Tc表示包括所有输入神经元、隐藏层神经元和输出神经元的网络连接总数。

对于具有最大隐藏层神经元个数Jmax的3层RBFNN结构,Tc和Ac的计算方式分别为

Tc=I×Jmax+Jmax×1=(I+1)×Jmax

(8)

Ac=I×J+J×1=(I+1)×J

(9)

在获得紧凑且泛化能力良好的RBFNN体系结构后,基于目标函数对网络结构进行自调整,调整规则为

(10)

式中ε1和ε2表示阈值因子,ε1设定为0.3,ε2设定为0.7。

2.3 下层目标:网络权值优化

SO-RBFNN训练的主要困难是获取最优的一组参数,即网络的中心、宽度、输出层与隐藏层之间的权向量,统一记为W。神经元之间的信息是单向传递的,而信息强度主要依靠神经元之间的连接权值,即实数加权来表示,因此,将网络中所有的连接权向量W视为较低层次的决策变量,表达形式如图2所示。算法的下层目标是对给定网络结构的RBFNN权值进行优化,为了保证算法的快速收敛,本文提出了基于局部优化和全局优化的独立优化机制。

2.3.1 局部网络权值优化

局部优化的任务是训练RBF子网络的连接权值,在这里,选择LM作为底层局部优化器,原因是它是一种优秀的基于导数的方法,收敛速度快,稳定性好。对给定的网络架构h,设置第k个子网络目标函数为

(11)

式中:P为训练集中样本个数;k,p为第k个子网络中第p个样本的网络输出;yk,p为相应的目标输出。最小化目标函数,即

(12)

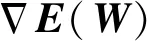
(13)

J(W)为雅可比矩阵,公式为

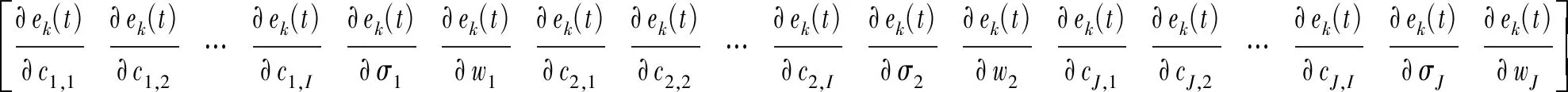
(14)

式中:ek(t)表示第k个子网络在t时刻的网络误差;cJ,1为第J个神经元中心的第1个元素,并且

(15)

假设H(W)很小,则Hessian矩阵近似为

(16)

将式(13) (16)代入式(12),得到

ΔW=[JΤ(t)J(t)]-1JΤ(t)ek(t)

(17)

JΤ(t)J(t)可能是不可逆的,因此,使用近似Hessian矩阵

ΔW=[JΤ(t)J(t)+μI]-1JΤ(t)ek(t)

(18)

式中:I为单位矩阵;μ表示一个大于0的参数。μ较大时,算法变为最陡下降法,而μ较小时,算法变为高斯牛顿法。在本文中,初始化μ为0.01。

2.3.2 全局组合系数优化

全局损失函数egl定义为真实输出与预测输出之间的差值,公式为

egl(t)=y(t)-tr(t)

(19)

将式(3)代入式(19),可以将全局损失函数改写为

egl(t)=y(t)-tr(t)=y(t)-[1(t)1(t)+2(t)2(t)+…+k(t)k(t)]=

(20)

式中ei(t)定义为第i个子网络预测输出与目标输出的差值,即

ei(t)=yi(t)-i(t)

(21)

则

(22)

i(t)=ei(t)-ek(t)

(23)

由式(20)推导出的损失函数可进一步简化为

(24)

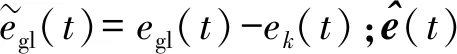
(25)

(26)

(27)

注1全局叠加系数的更新是一个线性差分方程,全局损失通过从多个子网络中收集信息提高收敛速度和性能。

注2通过定义并更新全局损失函数,系统无须等待每个子网络在系统收敛之前收敛,有效避免了梯度消失问题。

注3将训练过程和测试过程集成到一个系统中,上层框架用来自调整网络结构,降低网络复杂度,下层框架用来优化子网络的连接权值和线性组合的系数。通过持续交互、进化学习,有效解决了过拟合和欠拟合问题。

3 实验结果与分析

为了证明所提Hb-SRBFNN-OL的可行性,本文给出了多个分类任务和预测任务的测试结果与分析。下面将Hb-SRBFNN-OL算法用于从UCI机器学习库中选择的4个基准分类问题,并将其用于Lorenz混沌时间序列预测和污水处理过程中出水总磷(total phosphorus, TP)质量浓度预测的实际问题。为了进一步说明本文所提方法的优越性,将其与现有多种算法进行了比较。

所有实验均在Microsoft Windows 10.0操作系统、时钟速度为3.6 GHz、RAM为32 GB的计算机上使用MATLAB 2020b软件运行并通过均方根误差(root mean square error, RMSE)测量其性能。

3.1 Hb-SRBFNN-OL算法用于分类任务的实验结果与分析

3.1.1 实验设置

在本节实验中,下层优化器使用的LM方法中的参数设置如下:预定阈值为0.01, 最大迭代步数为20,μ=0.001 5。 所有数据集的输入标准化为[-1,1],采用“赢家通吃”策略,输出激活度最高的类别, 实验数据集及详细参数如表1所示。在本实验中,所有数据集被分成两部分:随机选择85%作为训练集,剩余15%作为测试集。在上层优化器提供网络结构的基础上,下层优化器使用训练集训练子网络权值,并将权值结果反馈至上层优化器,用以测试集测试Hb-SRBFNN-OL的泛化性能。

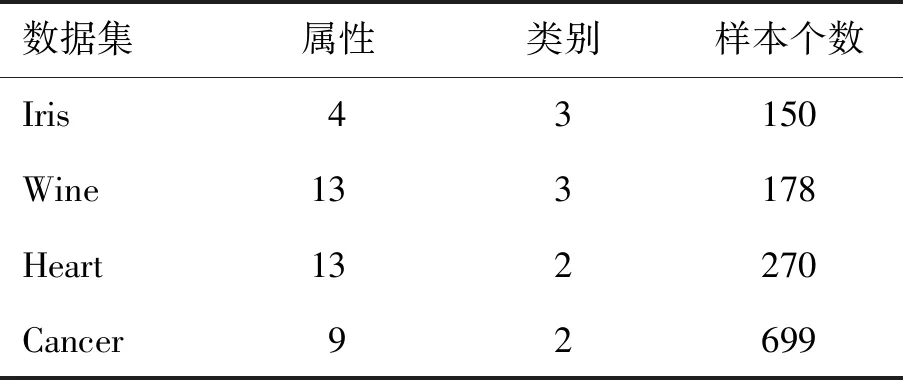
表1 数据集的描述

3.1.2 实验结果与分析

每个实例的所有实验具有相同的初始参数,通过对所有数据集多次独立运行,计算连续30次实验的统计结果。表2为使用Hb-SRBFNN-OL算法进行训练和测试的错误率、隐藏层神经元数量以及运行时间的统计结果,表中给出了训练和测试错误率的平均值和标准差(standard deviation, SD)。此外,还给出了隐藏层神经元个数的最小值和SD以及平均运行时间。

表2 Hb-SRBFNN-OL算法的训练和测试结果

分析表2,不难得出以下结论:1) 与以往建模方式不同,本文将训练过程和测试过程整合成一个总系统,通过上下2层交互学习,得到最优的网络结构和网络参数。测试误差率比训练误差率小得多,可见本文所提方法可以有效地避免过拟合。Hb-SRBFNN-OL算法在测试误差率足够小的情况下,对4种分类问题都具有较好的泛化能力,这也进一步表明,Hb-SRBFNN-OL算法能够在过拟合和欠拟合之间取得很好的平衡。 2) Hb-SRBFNN-OL算法同时考虑训练集和测试集,基于此,自适应动态调整RBFNN结构和连接权值,从而得到针对每个分类任务的最紧凑的网络结构。

为了进一步证明Hb-SRBFNN-OL算法的优越性,基于表1中的3个数据集,与单层学习算法进行了比较。 其中,粒子群优化算法(particle swarm optimization,PSO)、鲸鱼优化算法(whale optimization algorithm,WOA)[9]等元启发式方法均采用固定网络结构,隐藏层神经元的数量根据2×I+1选择,I表示数据集中属性的个数,实验结果如表3所示。

表3 与其他单层模型在分类任务上的对比结果

从表3中可以看出,在Wine、Heart和Cancer这3个基准数据集上,Hb-SRBFNN-OL算法在分类准确率平均值和最佳值方面明显优于PSO、WOA等元启发式方法且所需要的隐藏层神经元数量最少。需要特别说明的是,由于本文所提算法的下层优化器选择LM方法,在网络权值调整过程中需要计算并存储Hessian矩阵,增加了计算量。因此,在除Wine数据集之外的2个实例中,Hb-SRBFNN-OL算法的运行时间都稍长于WOA算法,并且无论在网络结构和分类准确率方面都充分证明了其在分类任务中的优越性。

3.2 Hb-SRBFNN-OL算法用于Lorenz混沌时间序列预测任务的实验结果与分析

在本节中,将Hb-SRBFNN-OL算法应用于Lorenz混沌时间序列的预测。Lorenz时间序列系统是一种大气对流数学模型,并且是一个高度非线性的三维系统,已被广泛用作评价学习算法性能[24-25],定义为

(28)

式中:a1、a2、a3为Lorenz时间序列中的参数,a1=10,a2=8,a3=8/3;X(t)、Y(t)和Z(t)表示三维空间向量。

在本实验中,使用由步长为0.01的四阶Runge-Kutta方法产生的9 000个数据样本,前6 000个样本作为训练数据,后3 000个样本作为测试数据,比率为2∶1。不失一般性地,网络结构均初始化为3-15-1,学习因子设置为0.5,中心c初始化为[-10,10]的随机数,宽度σ和隐藏层-输出层权值W分别初始化为[0,8]和[0,2]的随机数,最大迭代次数设置为200,预测结果如图3～6所示。图3为Hb-SRBFNN-OL算法的预测结果。图4为Hb-SRBFNN-OL算法与RBFNN、混合双层RBFNN (hybrid-bilevel RBFNN,Hb-RBFNN)、SO-RBFNN的预测误差。图5为用Lorenz时间预测时Hb-SRBFNN-OL模型中4个子网络的隐藏层神经元个数。从图4、5可以看出,Hb-SRBFNN-OL算法的预测性能良好,通过在迭代过程中不断调整网络结构,得到网络结构为7～9时,性能最好,并且测试误差保持在[-0.45,0.45]。图6 为线性系数变化相应的子模型误差结果,通过调整线性系数,避免了子网络中的梯度消失问题,加速了网络收敛。

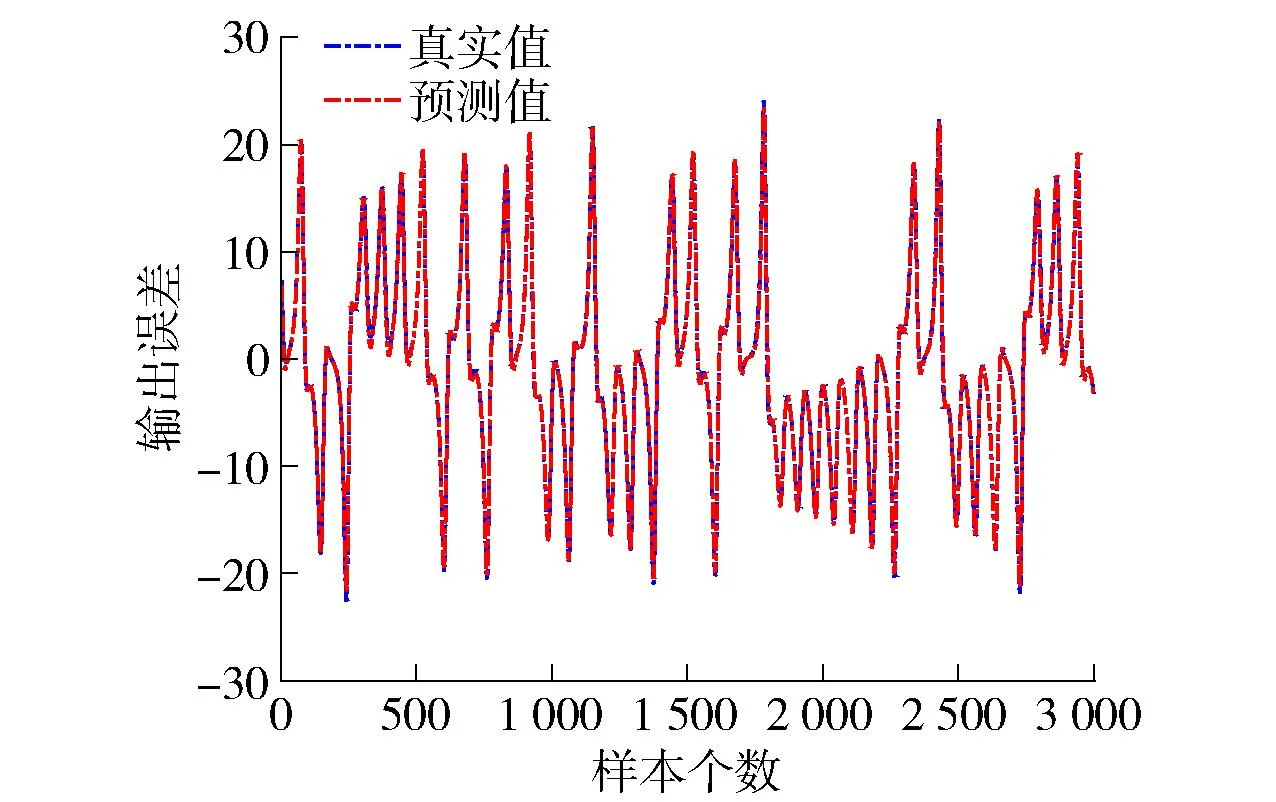
图3 Hb-SRBFNN-OL算法用于Lorenz时间序列预测的实验结果

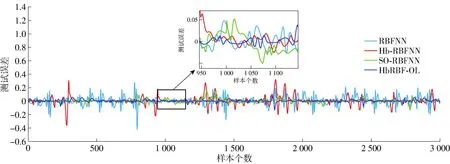
图4 不同方法用于Lorenz时间序列预测的测试误差

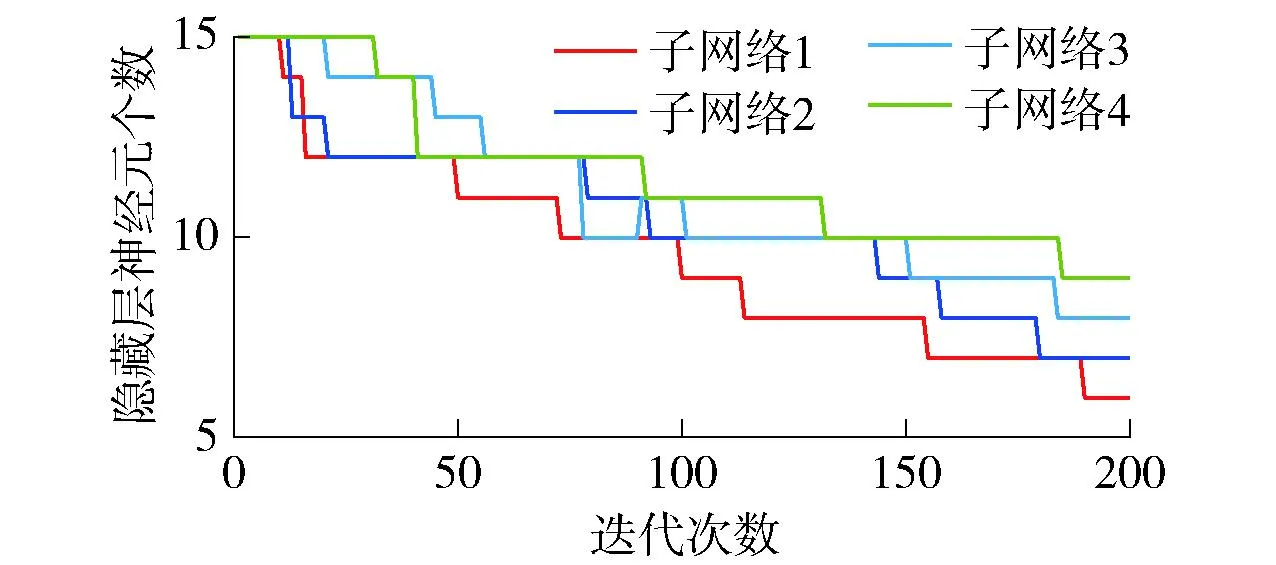
图5 子模型的隐藏层神经元个数(Lorenz时间序列预测)

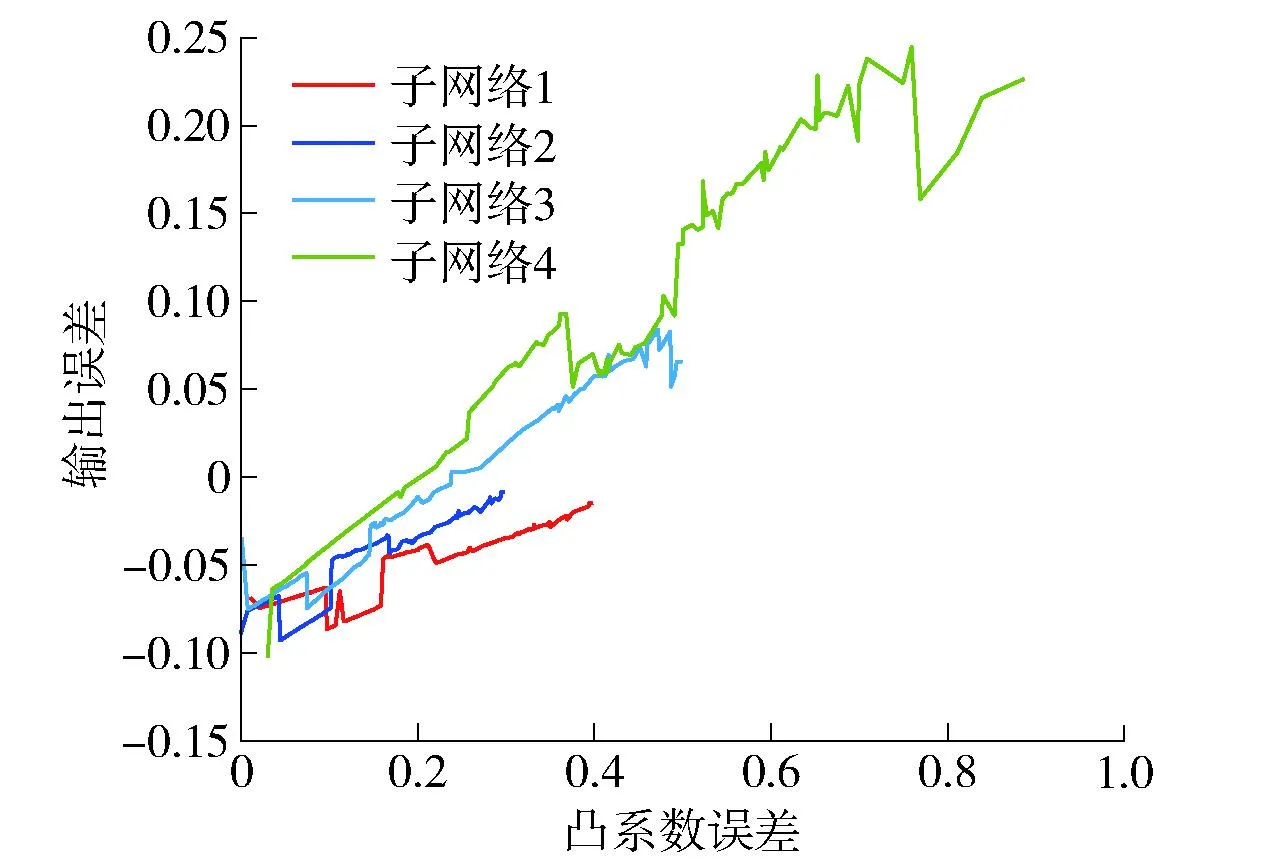
图6 子模型误差与系数关系(Lorenz时间序列预测)

为进一步验证Hb-SRBFNN-OL算法的有效性,将所得结果与RBFNN、Hb-RBFNN、SO-RBFNN这3种算法进行比较。以80次仿真实验结果的平均值作为最终结果,详细对比结果如表4所示。可以看出,Hb-SRBFNN-OL算法中第1个子网络的平均运行时间为36.16 s,在所有对比算法中时间是最短的,训练时间提高了30.49%～54.18%,充分说明更新全局损失函数可以加快网络的学习速度。主要原因是通过调整全局线性系数代替子网络参数,使得网络不必等待所有子网络收敛。此外,测试集的RMSE保持在[0.001 5～0.005 0],与其他3种算法相比,降低了38.22%～39.56%。基于表4的分析结果,不难得出结论,本文所提出的Hb-SRBFNN-OL算法能够以更高的精度逼近Lorenz系统,并且具有更紧凑的网络和更好的泛化能力。

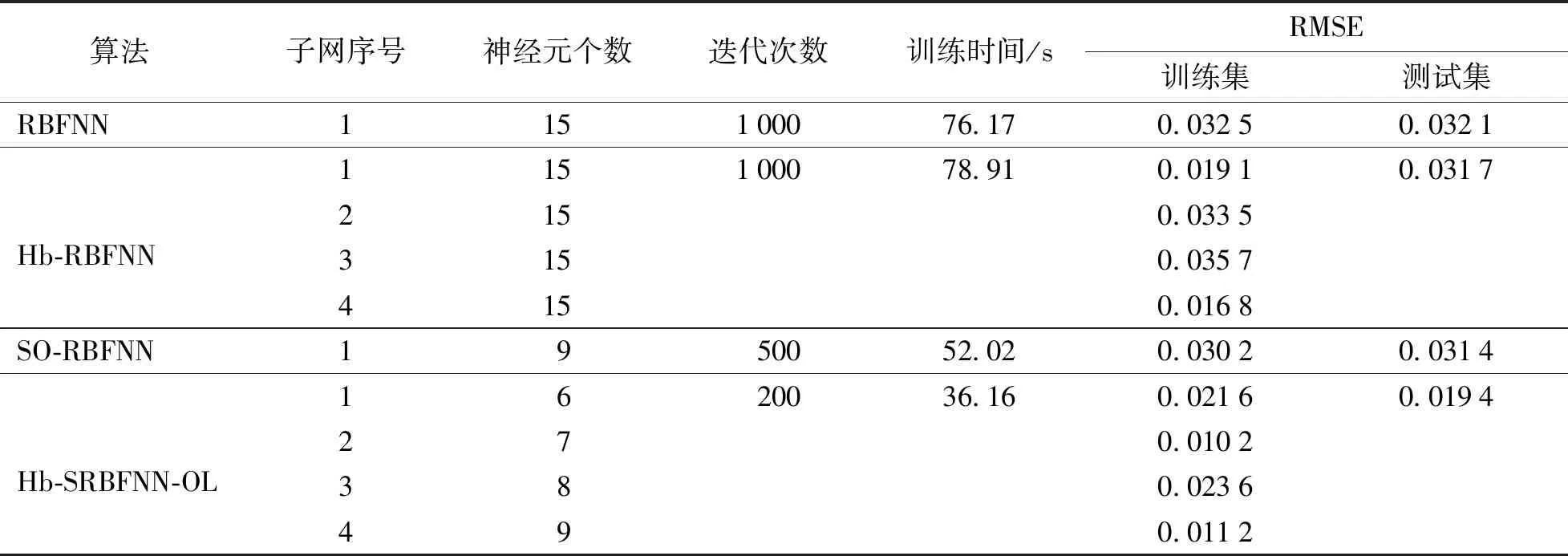
表4 Lorenz时间序列预测的不同算法比较

3.3 污水处理过程出水TP质量浓度预测

出水TP质量浓度是评价污水处理过程性能的一个重要参数。然而,由于活性污泥法的生物特性,出水TP的测定非常困难。因此,本实验采用所提出的Hb-SRBFNN-OL算法预测出水TP质量浓度。

实验采用北京某小型污水处理厂2016年1月至6月的60 000组数据,由于测量精度、操作方法等因素的影响,所采集的数据存在一定的误差。若对未处理的数据直接建模,必然会导致系统性能较差。为了保证预测结果的可靠性和准确性,先对异常数据进行剔除。最终,随机选取其中的10 000组数据作为训练样本,3 000组数据作为测试样本。

在本实验中,利用主成分分析方法选取预测模型输入:温度(T)、氧化还原电位(oxidation reduction potential,ORP)、溶解氧(dissolved oxygen,DO)、总悬浮固体(total suspended solids,TSS)以及pH。模型训练分为两部分:1) 下层模型用于训练子网络权值,利用LM方法训练RBFNN子网络中的参数,利用全局损失函数训练组合线性系数;2) 上层模型用于训练网络结构,利用网络复杂度和测试误差组成的损失函数对隐藏层神经元个数进行自适应调整,获得紧凑且泛化性能较好的预测模型,实验结果如图7～10所示。

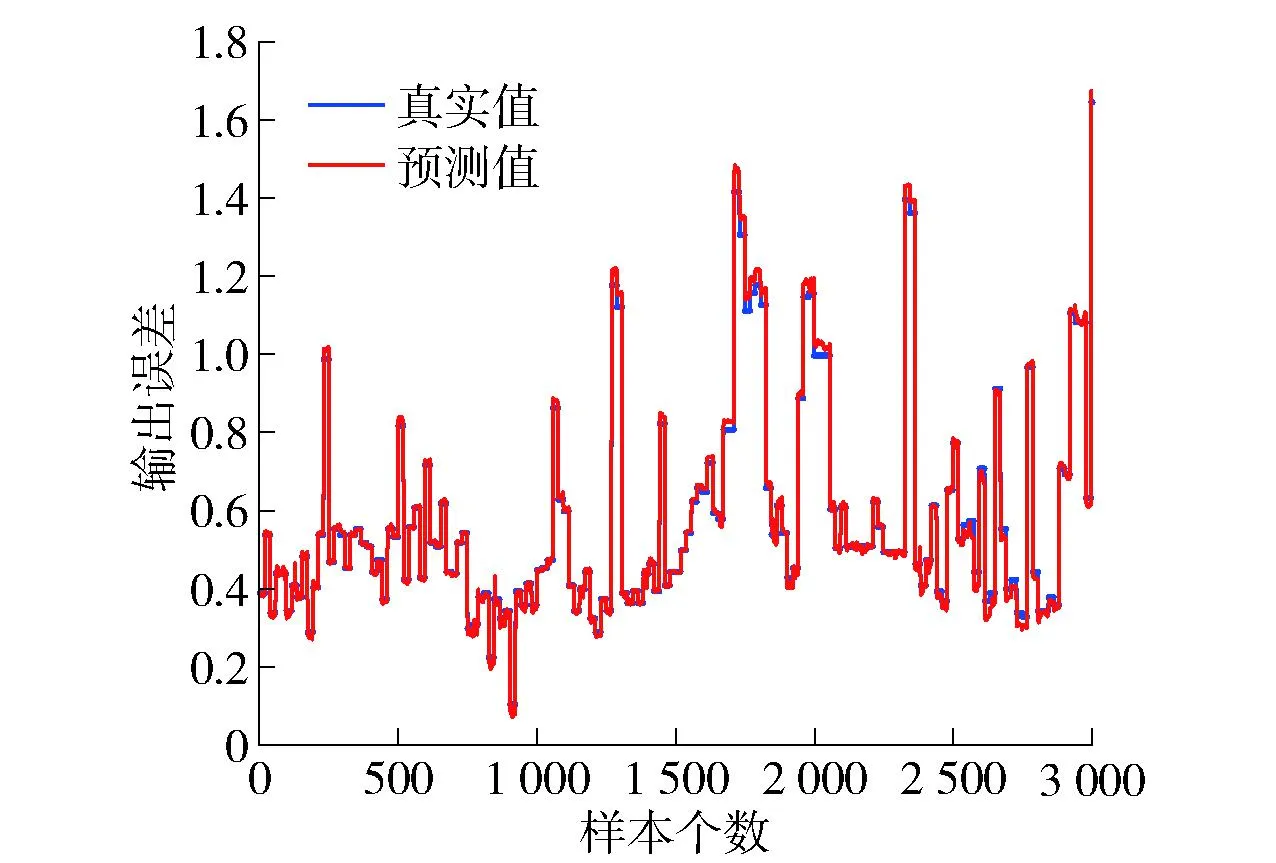
图7 Hb-SRBFNN-OL算法用于TP质量浓度预测的实验结果

从图7中可以看出,本文所提算法有很好的拟合效果。图8和图9分别为Hb-SRBFNN-OL与RBFNN、Hb-RBFNN、SO-RBFNN的预测误差及Hb-SRBFNN-OL模型中4个子网络的隐藏层神经元个数。从图中可以看出,Hb-SRBFNN-OL算法可以较好地预测TP质量浓度,预测误差较小,保持在[-0.02～0.02]。这主要是由于该算法基于结构复杂度和测试误差将参数调整和结构设计结合在一起,把模型更新转换成优化问题,并根据优化结果确定网络的最佳结构,有效地平衡了过拟合和欠拟合问题,使其泛化性能得到提高。图10为线性系数的更新过程。从图中可以看出,随着系数的不断调整,子网络误差不断更新,通过始终保持总和不变降低了运算量,保证了Hb-SRBFNN-OL算法的快速收敛和成功应用。

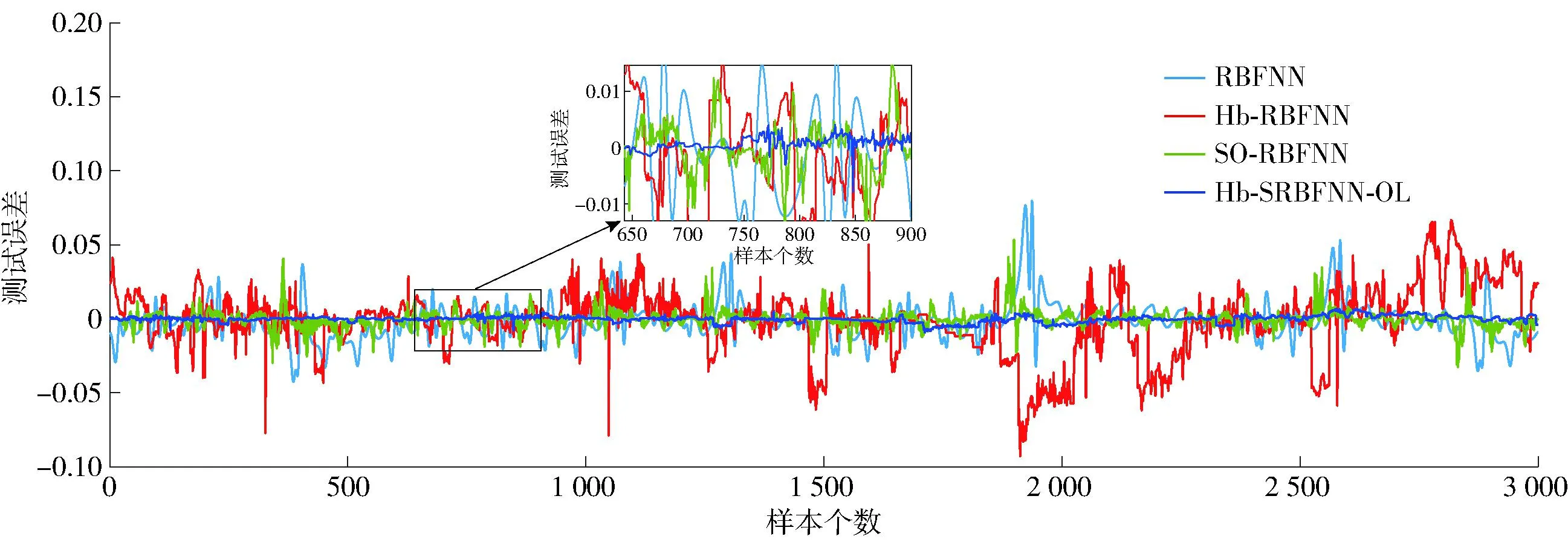
图8 不同方法用于TP质量浓度预测的测试误差

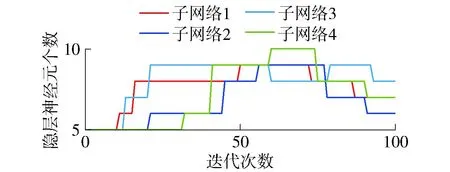
图9 子模型的隐藏层神经元个数(TP质量浓度预测)

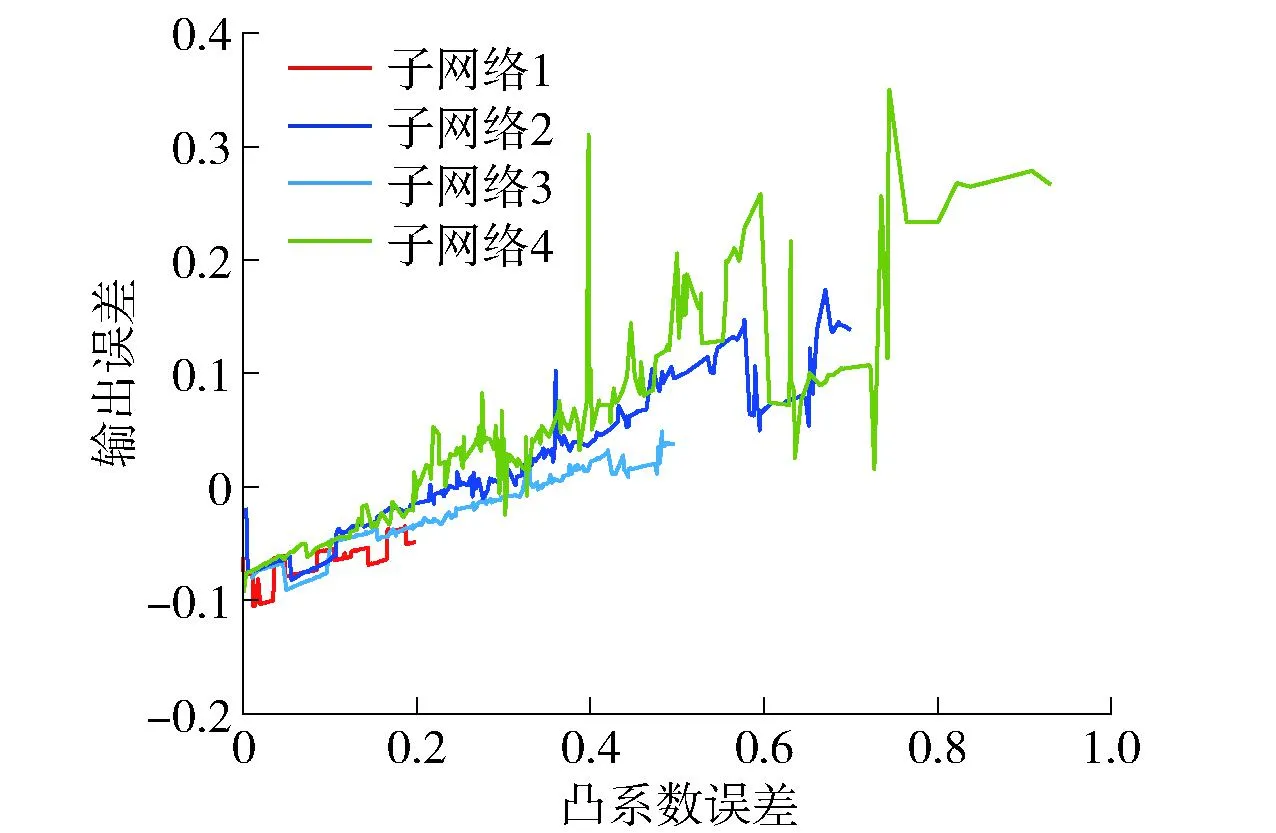
图10 子模型误差与系数的关系(TP质量浓度预测)

为避免实验结果带来的随机性,同时,为了验证算法的整体性能,将4种算法独立运行60次,并求取平均值,详细对比结果如表5所示。可以看出,Hb-SRBFNN-OL算法能较好地预测目标函数的值,并且具有最小的RMSE平均值。同时,该算法可以随着样本数据的变化自适应调整网络结构,使得RBF网络结构更加紧凑。最重要的是通过调整线性组合的全局线性系数而非网络参数,加速了网络收敛,这直接导致了Hb-SRBFNN-OL算法的预测时间最短。从表中也可看出,网络的训练时间与SO-RBFNN算法和RBFNN算法相比分别提高了32.61%和43.99%。上述结果表明,Hb-SRBFNN-OL算法在预测出水TP质量浓度方面比其他对比方法更合适、更有效。

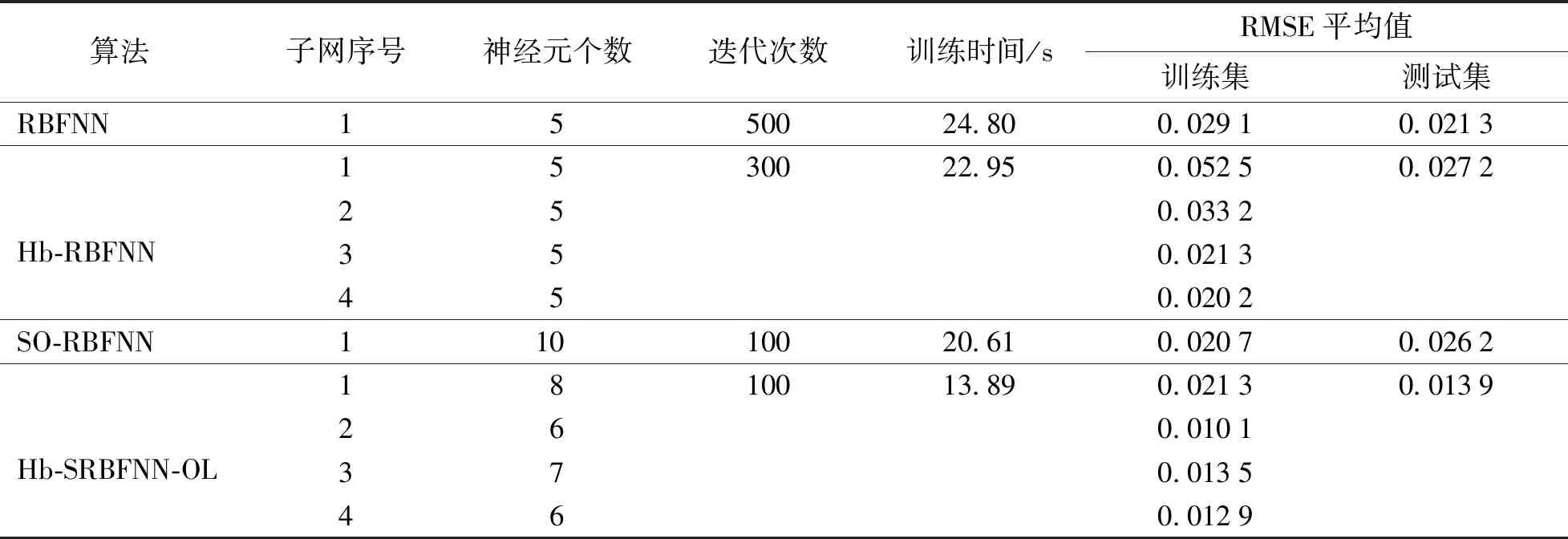
表5 TP质量浓度预测的不同算法比较

4 讨论

本文的目的是开发一种有效的进化学习机制来有效解决过拟合和欠拟合问题。实验结果表明,Hb-SRBFNN-OL算法的性能优于现有的一些方法。其主要贡献如下:

1) 学习速度快。Hb-SRBFNN-OL的关键问题是学习速度,本文提出以全局损失函数代替局部损失函数策略以调整网络参数,无须等待所有RBFNN收敛,有效避免了网络训练中的梯度消失问题。此外,系数的更新公式为差分方程,计算简单。表4、5中的结果表明,Hb-SRBFNN-OL算法比现有的对比方法有更快的学习速度。

2) 泛化能力强。泛化性能是Hb-SRBFNN-OL算法的另一个重要组成部分。混合双层进化学习机制可以兼顾训练过程和测试过程,通过持续交互更新网络参数和网络结构,克服了传统方法先训练后测试的弊端,有效解决了过拟合和欠拟合问题。

此外,在进行网络结构自组织时,Hb-SRBFNN-OL算法基于网络复杂度和测试误差调整隐藏层神经元个数,而在选择系数c1、c2时,始终没有成熟的理论依据,因为测试误差最小为最终目标,故尝试{ε1,ε2}={(0.5;0.4;0.3;0.2;0.1),(0.5;0.6;0.7;0.8;0.9)}时的网络预测结果。结果表明,当ε1=0.3,ε2=0.7时,所提出的Hb-SRBFNN-OL算法能够获得比其他方法更好的预测精度。另外,在上述TP质量浓度预测实验中,本文提出的Hb-SRBFNN-OL算法可以获得比同类算法更快的学习速度和更小的测试误差。

5 结论

1) 针对神经网络训练过程中过拟合和欠拟合难以取得平衡的问题,本文构建了一个混合双层进化学习模型。针对该双层学习模型,基于进化学习机制,提出了一种交互进化学习算法Hb-SRBFNN-OL。上层基于网络复杂度和测试误差优化网络结构,以便得到该场景下最精简紧凑的网络结构;下层基于训练误差对网络参数进行调整,得到一组最优的连接权值,以便提高准确率和泛化能力。此外,提出了线性叠加多层神经网络结构的思路,用系数组合的全局损失函数代替各个子网络的局部损失函数的策略进行进化学习迭代更新,加速了学习过程。

2) 通过在4个分类任务和2个预测问题上进行实验,并与其他现存的多种算法进行比较,结果表明,文中所提算法获得的SO-RBFNN结构更紧凑,泛化能力更强,并且预测准确率最高可提升30%,为工业过程中的预测和分类任务提供了一个更加灵活、开放、准确可靠的框架。

3) 未来将进一步开展以下两方面工作:进一步提高模型精度,考虑使用粒子群优化、遗传算法等启发式策略,寻找最优的网络结构;进一步降低双层学习算法的计算成本,开发极限学习机等非迭代学习算法,得到神经网络的最优连接权值。