基于岩石物性引导的地球物理联合反演研究
2024-01-08连晟程正璞罗旋李敬杰田蒲源
连晟,程正璞,罗旋,李敬杰,田蒲源
(1.中国地质调查局 水文地质环境地质调查中心,河北 保定 071051; 2.天津市地热资源勘查开发工程研究中心,天津 300300)
0 引言
作为深地资源勘探中重要的定量解释工作,地球物理反演通过地球物理观测数据(重力数据、磁法数据、地震数据和电磁数据)反推地下场源的空间分布情况,提供目标地质构造的物性和几何形态等特征信息。然而由于反演的多解性和单一地球物理方法的局限性等问题,导致了反演获得的结果与真实地下结构存在不同程度的差异。地球物理反演多解性问题主要是由于有限的观测数据量、观测数据的离散化、观测数据包含的随机噪声以及地球物理场自身的等效性。为改善反演多解性和单一方法的局限性,获得可靠的反演结果,融合多种地球物理场信息,并充分考虑岩石地球物理测试结果,进行多种地球物理场联合反演被认为是符合实际规律的一种解决方案。
基于空间分布结构性耦合的联合反演方法,由于强调结构上的相似性,不依赖于岩石物性间关系,应用更加广泛。Gallardo等[1]提出了交叉梯度函数,该方法通过对不同物性梯度之间叉乘来识别结构边界,实现了重、磁、电、震4种方法的交叉梯度联合反演;Moorkamp等[2]实现了重力、大地电磁和地震交叉梯度联合反演和岩石物性约束反演,并对二者进行了对比研究;李桐林等[3]实现了部分区域约束下的交叉梯度多种地球物理数据联合反演。
通过岩石物性实验室测试得到的地球物理参数是最为精确的方式之一,在实验基础上通过理论推导,部分岩石物性参数之间存在明确的函数关系,例如密度和地震波速度之间存在明确的正比关系,但大量的地球物理参数之间并不存在明确的函数关系,仅岩石物性测试尺度中存在统计学相关性。如何将该种来自岩石物理测试获得的地球物理参数之间的统计学关系应用到地球物理联合反演中,学者们做了大量研究工作。张磊[4]基于正则化思想利用宽范围岩石物性约束方案实现了MT与重力联合反演。Sun等[5]将岩石地球物理先验信息在参数域利用模糊C聚类方案以参考聚类中心的方式融入反演过程,有效提高反演效果。此外,模糊C聚类算法在磁法、重力等数据反演中的应用均取得了良好效果[5-6]。易柯等[7]在经典最小结构模拟正则化约束的基础上开展了多地球物理参数的联合反演研究工作。随着大数据的发展考虑岩性约束的联合反演方案应用越来越广泛,其中利用有限混合模型,将不同岩石样本物性测试得到的统计学分布特征用简单的概率密度函数模拟,使得分析结果具有较好的空间连续性和稳定性[8]。学术及实践中发展了大量类型的有限混合模型,其中最具代表性的是高斯混合模型。高斯混合模型凭借形式简单、计算方便等优势,成为广泛应用于科学研究有限混合模型[9],Astic等[9]使用高斯混合模型实现了用岩石先验信息引导重力、磁法联合一维反演。Di-Giuseppe等[10-11]基于共网格技术提出了一种后反演(post-inverstion)方案,该方案将k均值聚类分析技术应用于先前获得的单变量反演的二维地震折射层析和可控源音频大地电磁反演剖面,通过定量分析不同参数间的相关程度,识别了聚类后的数据集与岩性的对应关系。Li等[6]将聚类技术应用于大地电磁三维反演结果,识别和归类了反演结果中的地质构造,达到了地质分异(geology differentiation)的目的。
本研究实现了高斯混合模型进行岩石物理和地质引导的多种地球物理场联合反演以及基于共网格的单变量反演模型的多元物理信息k均值聚类的地质分异,达到了多种地球物理场联合反演及数据融合分析的目的。本文仅就联合反演部分进行展开,将高斯混合模型作为岩石地球物理的约束方案,在地震勘查的结构基础上,联合重磁、大地电磁法数据进行联合反演。
1 重力、磁法和大地电磁正反演理论
本文重力正演计算采用曾华霖[12]给出的解析算法,磁法正演使用管志宁[13]给出的算法。大地电磁正演使用基于六面体网格剖分的矢量有限元法[14]。
φ=φd+λφm,
(1)
其中:φd为数据拟合项,表达式如下:
(2)
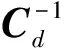
φm为模型平滑约束项:
(3)
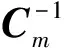
正则化反演的实现可以认为是一个寻优过程,其目标是找到一个使目标函数最小的地球物理模型m,该地球物理优化问题的形式为[13]
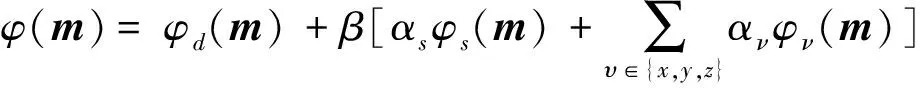
(4)
(5)
由图6可知,降低购房者购买被动房的增量成本可有效降低购房者购买普通房的概率,即提高购房者购买被动房的意愿,间接说明可提高对购房者激励的有效性,反之,若购买被动房的增量成本增加会降低被动房的购买意愿。
2 高斯混合模型及岩性约束
为实现岩石物性对地球物理反演的约束,首先需要将岩石物理测量的物性参数如密度、磁导率和电导率等测量结果进行数字化表达,本次研究使用了高斯分布来描述某种岩石物性参数的概率分布规律,同时利用不同岩性的高斯分布相叠加后得到多岩性单地球物理参数的高斯混合模型。若M个岩石样本均测量了4个地球物理参数(密度、磁化率、电阻率、速度),这些岩石样本可以分为泥岩、砂岩、花岗岩3种类型,对应每个地球物理参数会有4个高斯混合模型,每个高斯混合模型有K=3个子高斯模型,其概率密度函数[9]为:
(6)
式中:K代表混合模型中子高斯模型的数量,即所测量岩石类别的个数;πk是第k个高斯分量的先验权值,该权值满足条件:
(7)
φ(x∣θk)是第k个高斯分量的高斯分布密度函数,表达式如下:
(8)
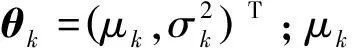
3 多地球物理岩性约束反演
地球物理联合反演问题使用Tikhonov反演方法,该方法将反演问题转化为一个最优化问题,其中描述岩石物性参数分布的高斯混合模型以负对数形式作为Tikhonov反演中的误差估计[9],该误差可以通过当前模型mi和参考模型mref之间的最小二乘误差来近似,该项误差和最小系数矩阵Ws需要在每次迭代时更新。动态参考模型和系数矩阵根据当前地球物理模型以及地质结构及岩石物理先验信息来确定[9,17]。
3.1 多地球物理岩性约束反演目标函数
多地球物理属性下岩性约束反演的目标函数用如下的最小二乘形式表示拟合误差:
(9)
其中:m为地球物理模型;β、αs、αν,p为正则化参数;φd(m)为包含多个地球物理属性的拟合误差;φs(m)为针对各模型的高斯混合模型拟合误差;φν,p(m)是对每个方向和物理属性的平滑项,其表达式分别为:
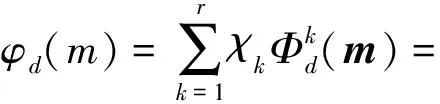
(10)
(11)
(12)
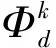
3.2 正则化参数的计算方式
反演目标函数中包含3个正则化参数β、αs、αν,p,计算中采取保持αν,p不变,仅更新β、αs来求解式(9)。在平滑项中,αν,p作为尺度参数控制着空间导数项,αν,p的数值采用对每个物理属性进行加权获得,用于均衡不同尺度(如密度、电导率和磁化率等)时,均衡平滑项对目标函数值的贡献,具体加权系数根据经验给定。
正则化参数β、αs的计算采用Astic等[9]的计算策略,对于多物理场情况,本次研究通过以下方式对其进行改变:当所有的地球物理数据拟合误差大于或者等于其目标值时,减小β的数值,当全部地球物理数据拟合误差都等于或低于其目标值时,则增加参数αs的数值。
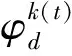
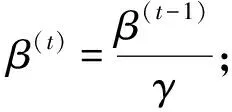
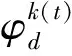
则参数αs按照式(13)增加其数值:
(13)
4 温度预测方法
本文选用与温度最为关联的电导率参数来进行温度场计算,温度与电导率之间的关系根据Arrhenius定律[18]表示为:
σ=σ0e-E0/kT,
(14)
其中:σ为电导率(岩石物理试验实测电导率),S/m;k为波尔兹曼常数0.8617×10-4ev/°K;E0为活化能eV;T为开氏温度;σ0为前指因子,不同温度、不同岩石其值不同;e为自然常数。这些参数可由实验室实验测得[19],一些岩石的活化能E0和前指因子σ0可参见表1。

表1 岩浆岩的活化能E0值与常数系数logσ0试验室测量结果
5 模型试算
基于以上反演理论及算法,采用C语言联合Python语言实现了基于岩性引导的联合反演计算,为检验算法有效性,本文进行了模型的单独反演和联合反演模型试验,设计模型如下:在电阻率为1 000 Ω·m、相对密度为0 g/cm3、异常体相对磁化率为0 SI的均匀半空间介质中,设置长方体异常体,长宽高为1 km×1 km×0.4 km,顶面距离地面1 km,相对密度为-0.2 g/cm3,相对磁化率为0.2 SI,电阻率为10 Ω·m,异常体的空间分布见图1所示;该理论模型由地下两部分组成,即块状体和背景值,两部分属性值的分布符合高斯混合模型分布,其中块状体密度为20%,背景值的分布密度为80%,密度/磁化率和密度/电阻率二维分布及高斯混合模型分布见图2。
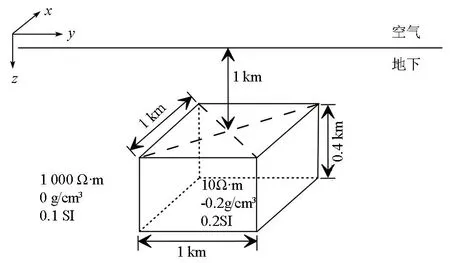
图1 正演模型参数
大地电磁正演观测数据频率为100~0.01 Hz之间的10个对数间隔频率,在正演计算结果中加入2%随机误差的合成数据;重磁反演的观测数据来自于在重磁三维理论正演计算结果中加入2%随机误差的合成数据,通过对重、磁、电合成数据进行基于高斯混合模型先验信息约束下的联合反演,反演的初始模型均使用均匀半空间模型,其半空间物性参数为:1e-4g/cm3、1e-4SI和1 000 Ω·m。磁法正反演过程所假设的磁性参数为:地球磁场强度50 000 nT与剖面夹角0°、剖面内磁倾角90°、地磁场倾角90°。
由以上3种方法的单独反演结果与联合反演结果对比(图3所示),可以在电阻率模型单独反演结果中看出异常面积大于真实模型,异常上下边界均偏差较大;在密度和磁化率单独反演结果中,无法准确识别异常体上下界面,异常体面积偏大,范围较理论模型有较大差距,异常体下部出现了一定范围的假异常,表明该类方法垂向分辨率较弱。通过联合反演得到的电阻率、密度、磁化率结果(图3b、d、f)显示与理论模型数值相比较,异常体边界位置、几何尺寸和物性参数值均更加接近理论模型,密度和磁化率联合反演结果上下界面位置比单独反演定位结果更加准确。通过以上分析,证明联合反演效果好于单独反演。
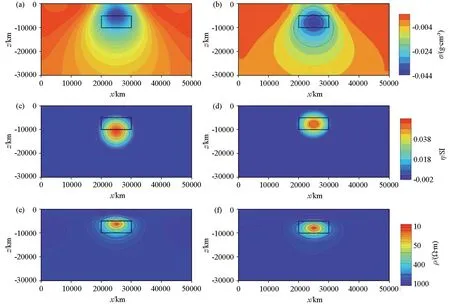
a—重力单独反演结果;b—长方体模型联合反演密度结果;c—磁法单独反演结果;d—长方体模型联合反演磁化率结果;e—大地电磁单独反演结果图;f—长方体模型联合反演电阻率结果
6 实际案例
为了验证该项技术的应用效果,在青海共和盆地进行了应用。青海共和盆地位于青藏高原东北缘,为高温地热异常盆地[20],现已建成我国干热岩勘探与开发示范研究区[21-22]。研究区位于青海共和盆地二级构造单元切吉凹陷东缘,切吉凹陷基底以三叠纪地层和印支期花岗岩为主,基底具东浅西深的斜坡带性质[20]。
研究区内进行了大地电磁、重力、二维地震等多种地球物理勘查,以位于切吉凹陷中部1条NE向综合测线为例介绍应用效果。该测线地震勘查结果(图4)显示覆盖层西厚东薄,多条断裂切穿基底,断裂多为西倾逆断层。共和组—咸水河组地层为砂岩和泥岩,最厚处达2 900 m,具有较好的保温效果。
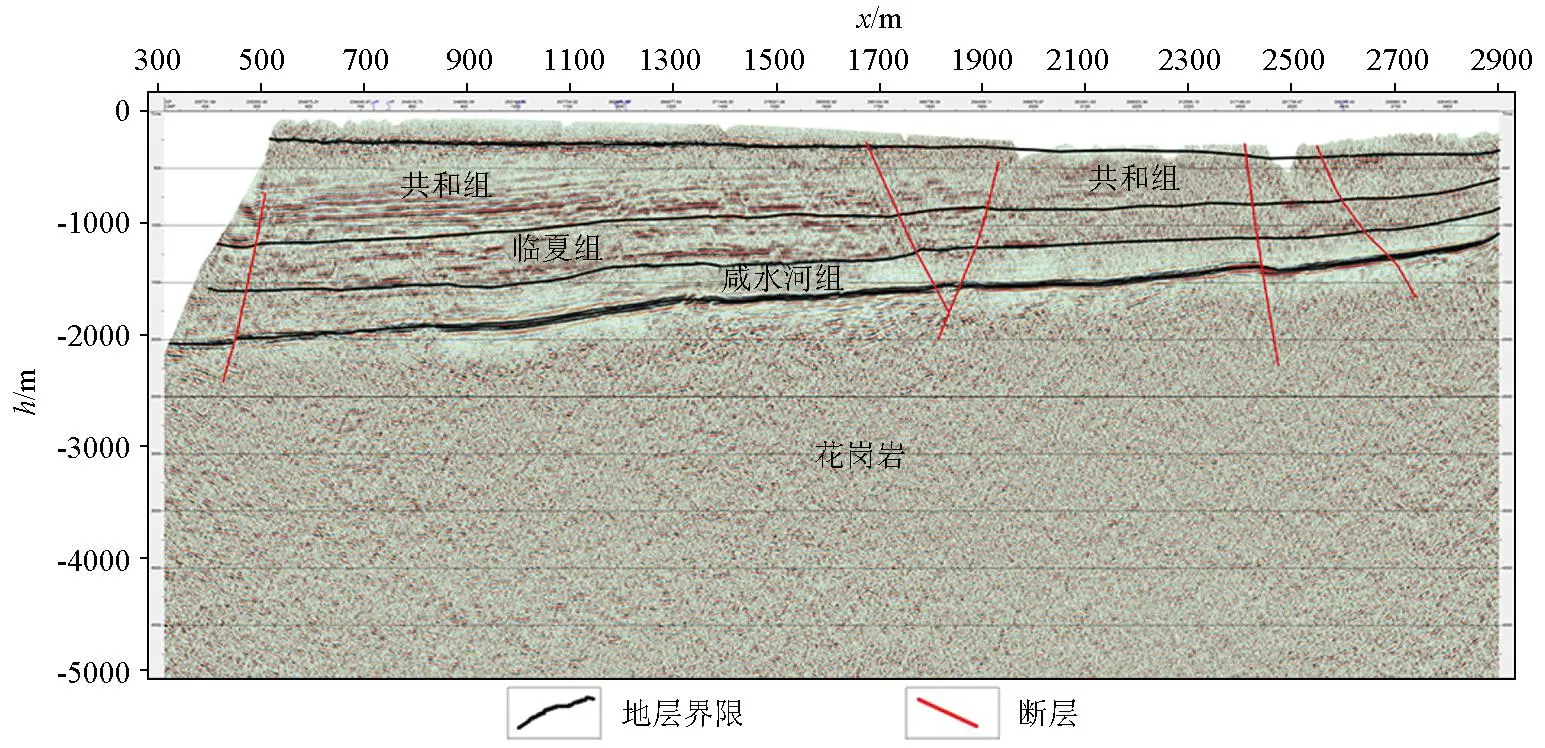
图4 共和盆地典型地震勘查结果
通过地震划分的地层作为模型结构约束,联合二维重力、大地电磁法两种数据进行联合反演,得到该条剖面的电阻率分布(图5)和密度分布(图6),由于该条测线磁法数据质量较差,故磁法数据没有加入该案例进行联合反演。综合分析认为共和组地层为次高阻、低密度层,具有一定的横向连续性,局部电阻率横向不均匀,推断为因断层发育导致的电阻率变化,横向西部厚度大、东部厚度略小,与地震勘探显示结构一致,该层重力反演结果显示为低密度响应;临夏组和咸水河组地层为低阻、低密度响应,西部埋深大、东部埋深小,电阻率横向连续性较好;下覆花岗岩为高阻、高密度特征。
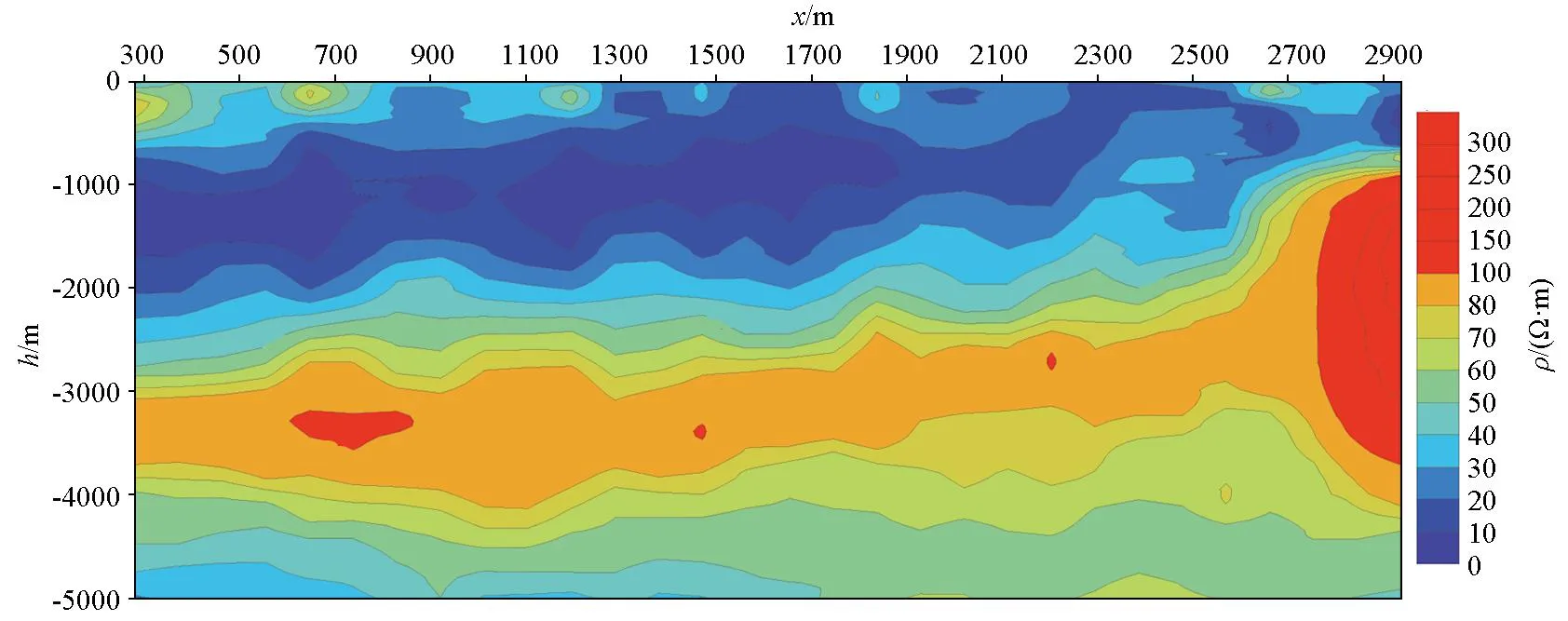
图5 研究区联合反演电阻率结果
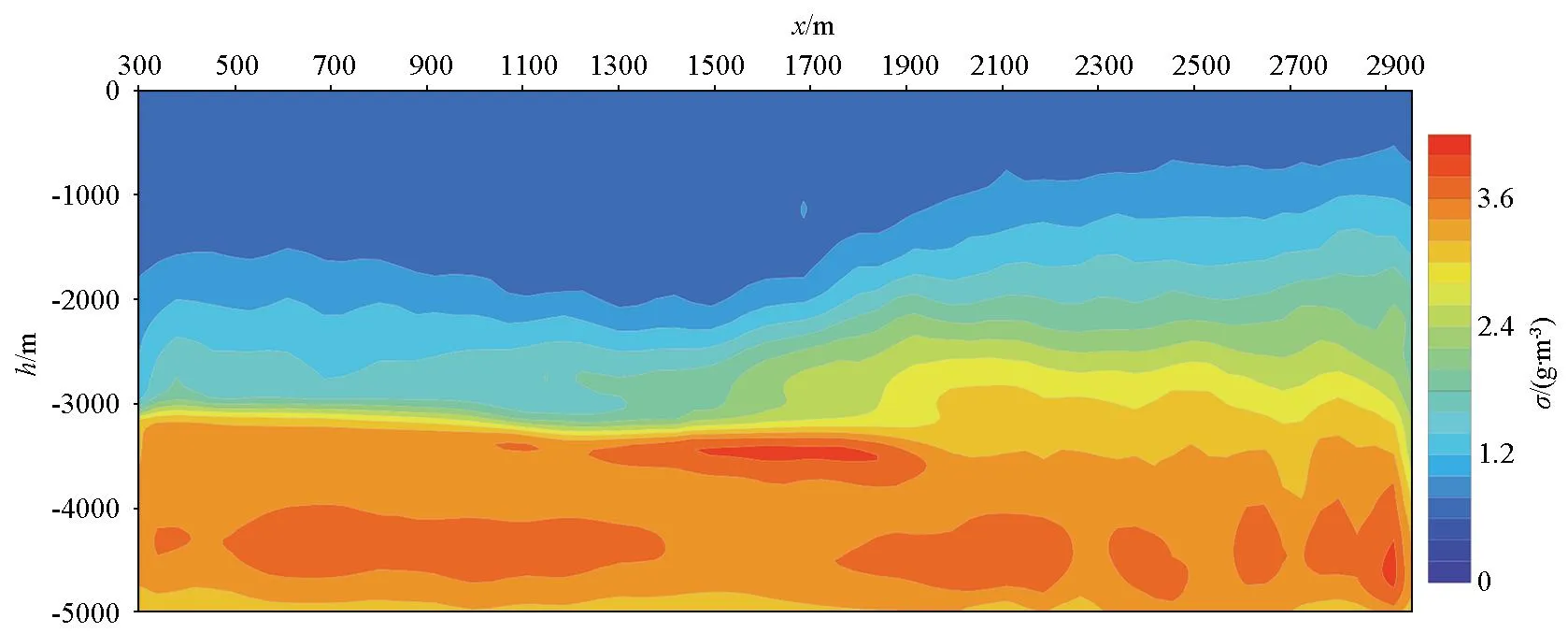
图6 研究区联合反演密度结果
从电阻率和密度交会(图7)及密度分布图中可见,密度由2个高斯分布组成,其均值分别为3.7 g/cm3和0.5 g/cm3,电阻率同样由2个高斯分布组成,其均值分别为20 Ω·m和70 Ω·m。
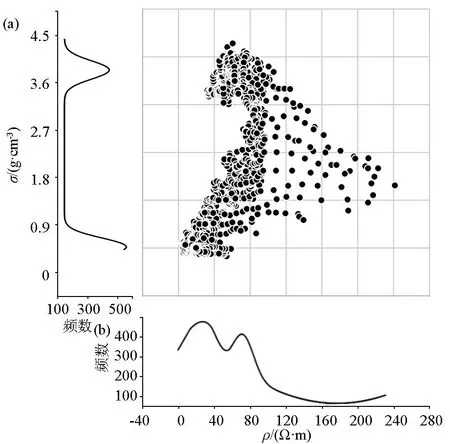
图7 密度和电阻率联合反演结果交会(a)及密度分布(b)
将联合反演后剖面的电阻率值利用式(13)计算得到剖面的温度场分布结果,由于上覆地层岩性主要为泥岩和砂岩,为区域内的保温层,其电阻率和温度对应关系不够明确,因此本项工作仅计算了该剖面覆盖层之下花岗岩地层的温度场分布(图8),其中活化能和前指因子σ0按照表1中实验室利用花岗岩测定的数值来进行计算,其中E0为0.9 eV,logσ0为-2.4 Ω-1cm-1。由于该温度场是通过电阻率剖面计算得来,其温度场分布特征规律与电阻率剖面特征基本一致,花岗岩中3 000~4 000 m深度范围内温度基本均匀,温度范围在200 ℃左右,等温线呈西低东高的特征,随着深度加深温度逐渐升高,到5 000 m深剖面西段温度达到280 ℃以上;但由于浅部地层电阻率较低,花岗岩顶部接近覆盖层的区域所计算温度场不符合地温场特征,造成该种形态的原因是由于温度场是通过电阻率直接计算得到,而该段处于电阻率从低向高变化的过渡带区域,需要进行针对的校正研究才能符合真实地温场特征。
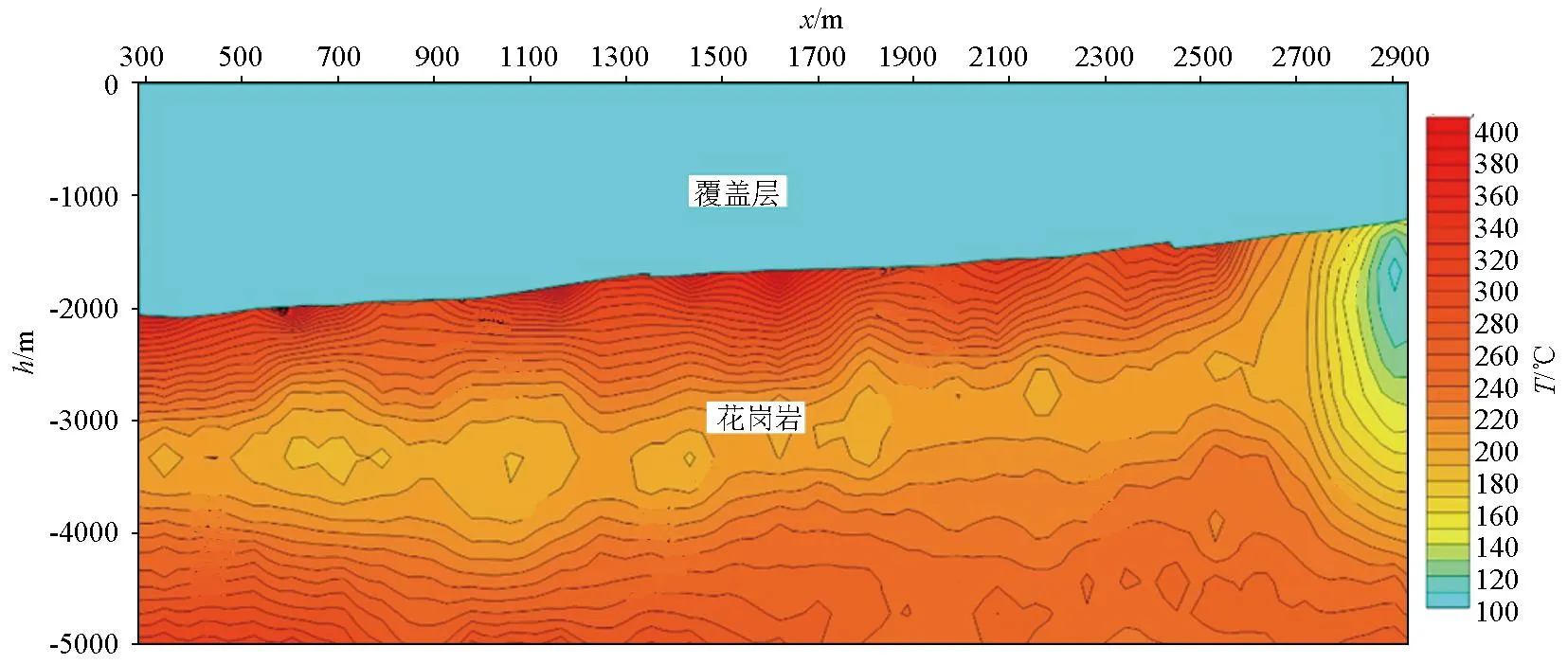
图8 温度—深度剖面
7 结论
1)利用高斯混合模型能够表征模型参数的多峰分布特点,将其用于联合反演连续地球物理变量和离散岩性。相比传统的反演算法,将岩石物性测量结果中同一岩性不同参数之间的统计学关系引入反演过程中,更加符合实际规律。
2)联合反演相对于单一反演不论在数值恢复能力还是在异常边界的刻画能力上都有较大程度的提高,使得反演结果具有较好的空间连续性。
3)基于约束的联合反演方案,虽然可以较好地将已知的结构信息和岩石物性分布规律置于反演过程中,反演结果与先验信息更加匹配,但所求得的反演最优解与单独反演相比,模型参数的小尺度变化被“平滑”,使得垂向分辨率变差。
4)直接将电阻率与温度之间的实验室测量参数应用在岩性简单的大尺度温度场,分布结果与钻孔测温结果基本相符,但在岩性过渡带位置,温度场与实际温度测量结果相差较大,需要进行校正研究,进行针对性校正后可以用于温度预测使用。
