卷积神经网络在山东金矿勘查预测中的应用

郑孝诚,张明华,,任伟

(1.中国地质大学(北京) 地球物理与信息技术学院,北京 100083;2.中国地质调查局 自然资源综合调查指挥中心,北京 100083)

0 引言

成矿预测是实现科学找矿、扩大资源储量的重要途径和方法[1]。从20世纪中叶开始,关于找矿的相关研究经历了从定性到定量、再到定位定量预测的发展阶段[2]。1975年,国际地质科学联合会推出了第一代标准矿产资源定量评价方法,包括区域价值估计法、体积估计法、丰度估计法、矿床模型法、德尔菲法和综合法等6种[3],这些方法主要是依靠从业者的相关经验来进行应用。但在应用中,因实际地质情况较为复杂,通过第一代标准矿产资源定量评价方法得到的变量太多,导致无法判断。针对这一问题,地质学者们设想通过减少变量来进行降维,将原有变量通过一些方法转化为数量更少的新变量。

1993年,由Singer提出的矿产资源的“三步”定量评估方法[4]逐渐成为了当时的主流方法,但该方法在实施过程中有较大的局限性,因为不同的成矿类型可能在相同的地质条件下产生。赵鹏大等[5-6]也提出了“三联式”资源定量预测与评价。随着计算机技术的发展,GIS技术开始应用在地质研究中,地质工作者们利用地质体或者矿体建立找矿模型,通过GIS技术来探究地质体和矿体之间的相互作用关系,从而进行成矿预测[7-8],或是将多重分形原理与成矿过程、矿产资源分布规律、矿产资源信息获取研究相结合,以“奇异性—广义自相似性—分形谱系”为核心进行非线性成矿预测[9]。周永章等[10-11]通过分析大数据和智能矿床模型研究的背景和进展,将机器学习应用到找矿预测中,奠定了大数据智能矿产资源预测与找矿理论的基础;并将机器学习用在安徽省兆吉口铅锌矿床预测的研究中,其预测的45、56号区域已被证实含矿,证明了卷积神经网络模型在其研究区域中已有的数据中是有效的。

为能够从宏观上预测山东部分地区的金矿分布情况,笔者尝试应用卷积神经网络这种机器学习方法来对山东部分地区的金矿分布进行圈定。本研究根据山东省某地金矿成矿区域的3×104km2范围内地质、矿产、地球物理、地球化学等实测专业数据资料进行卷积神经网络的训练,建立一套高效的卷积神经网络,可以有效识别出已知矿床分布的位置,进而将这套卷积神经网络用于山东省其他未知地区,进行金矿床分布位置(勘查靶区)的预测试验,得到较好的结果,其大部分已知金矿床勘探区的分布与网络输出的存在金矿床的高概率位置基本重合,验证了本文卷积神经网络方法技术的可行性。同时,通过输入不同数量的专业数据特征量对网络输出结果的影响研究,证实了更多的输入数据特征量可以明显提升网络预测结果的准确率和效率。本研究成果为海量多专业地质数据与卷积神经网络相结合进行隐伏矿产资源预测的可行性和有效性研究提供了依据。

1 数据准备

通常,在训练有监督的卷积神经网络模型的时候,会将数据划分为训练集、验证集和测试集,对原始数据进行三个集合的划分,是为了能够选出准确率最高的、泛化能力最佳的模型。

训练集:用来拟合模型,通过设置分类器的参数,训练分类模型。后续结合验证集作用时,会选出同一参数的不同取值,拟合出多个分类器。

验证集:当通过训练集训练出多个模型后,为了能找出效果最佳的模型,使用各个模型对验证集数据进行预测,并记录模型准确率。选出效果最佳的模型所对应的参数,即用来调整模型参数。

测试集:通过训练集和验证集得出最优模型后,使用测试集进行模型预测,用来衡量该最优模型的性能和分类能力。可以把测试集当做从来不存在的数据集,当已经确定模型参数后,使用测试集进行模型性能评价。

2 技术路线与数据预处理

以我国山东半岛中西部地区已知的金矿床资源量和储量数据以及当地的地质及物探、化探等7组数据作为标签特征,后增设了与金矿关系密切的5种元素的化探数据再次进行试验,将实际矿点作为标签,采用网格单元划分的方法,进行多专业数据赋值、网络学习和预测。图1为研究区区域地质图。

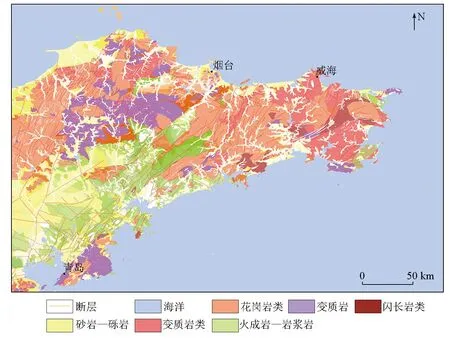
图1 研究区地质概况

首先,将典型金矿点及其周围区域根据经纬度划定测点,将划定测点上所对应的金矿含量以及12种标签特征罗列出来,利用计算机算法和程序处理划分训练集,并归纳总结出一套适用于该地区金矿勘查预测的网络层数和神经元数及属性参数相对固定的神经网络。多次测试之后得到某一阈值之下的最佳卷积神经网络,然后将这套网络算法应用到其他已知的金矿区进行预测正确性与准确性的测试。将所得到的卷积神经网络应用到测试集进行测试,在确定其应用性后,推广应用到其他类似地区实际的金矿勘查预测工作中。图2给出了具体流程。

图2 研究流程

对于相关特征数据的预处理,由于所选的特征中岩性与地质构造两种特征无法用数字定义,卷积神经网络训练过程中需要识别数字,所以首先要将岩性和地质构造定义为数字(表1)。例如岩性特征,在训练网络时是自己定义某种岩性的值,如把某点存在花岗岩,则定义该点的岩性为1,其他的岩性分别定义为2、3、4…,不明地质体定义为0。同理,地质构造也是根据上述条件来进行赋值。

表1 不同岩性和地质构造标签定义

任意选取训练集中的一个点,该点经度为122.28°,纬度为37.01°,在地质图上查询后得知该点处于上庄断裂,主要岩性为含砾砂岩—粉砂质黏土,则其对应的岩性和地质构造数据为14、4。

3 训练集划分

图3给出了所选训练集的位置。训练集取值经度范围为122.02°～122.51°,纬度范围为37.02°～37.41°,经纬度以0.01°为间隔进行取点。将图3中黑色测点的各项特征提取出来整合成训练集。

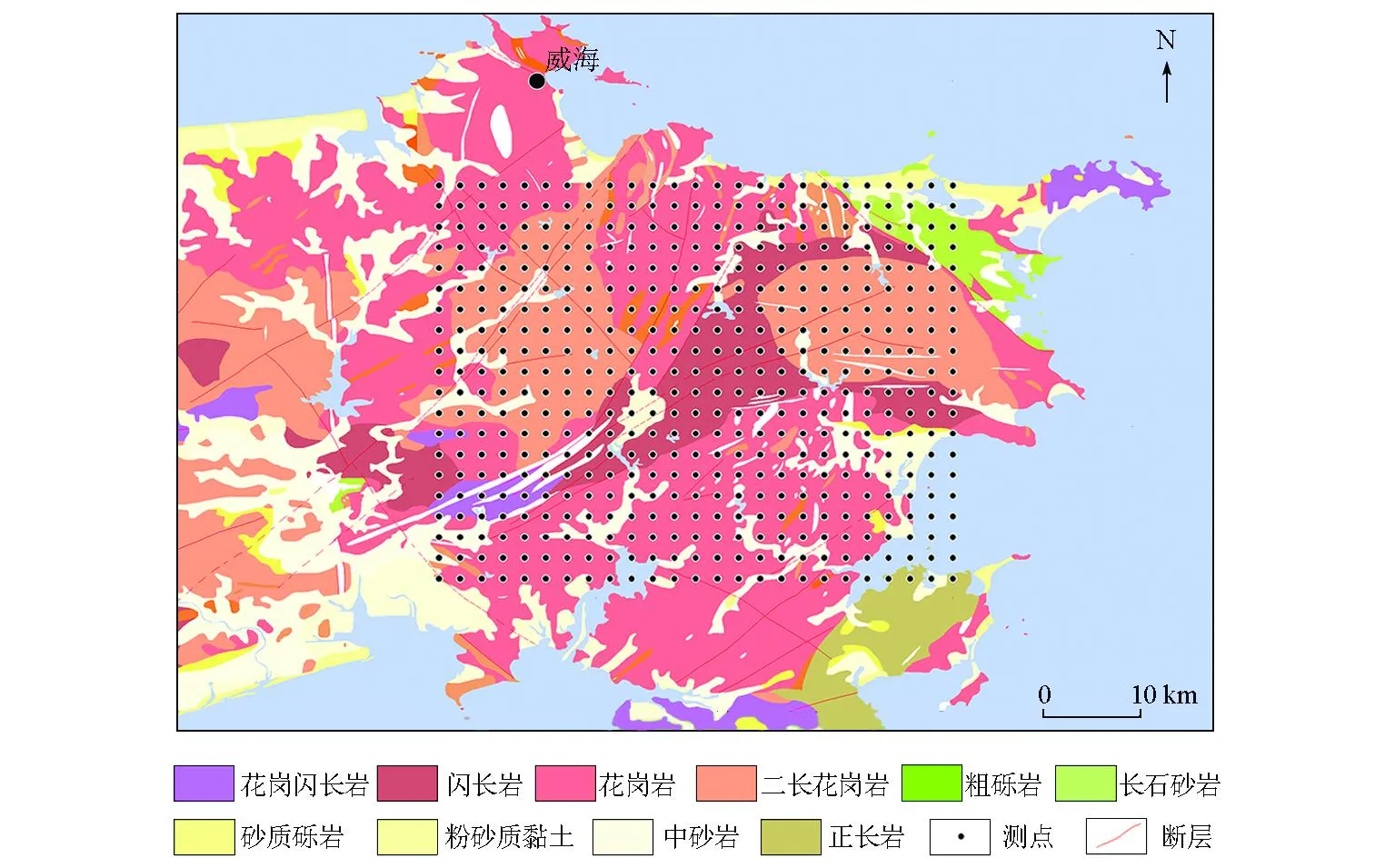
图3 训练集的点位区域

选择该区域的原因有以下几点:①训练集所在区域的中上部(烟台市牟平区)有几个典型的金矿点,区域内其他位置也存在少数金矿点;②该区域所掌握的数据比较详尽,在训练过程中容易得到好的模型;③该地区岩性十分丰富,地质构造也十分复杂,有利于训练网络的准确性。

为了对不同特征数据条件下训练出的卷积神经网络进行比较,选用测点的7种和12种特征数据分别训练对应的卷积神经网络。以研究区已知的金矿床资源量和储量数据以及当地岩性、磁异常、布格重力异常、自由空气异常、金异常及地形高程等7组数据作为标签特征,根据测点的经纬度提取出每个测点所对应的这7种数据,形成一个数据集合,命名为训练集1;然后增设与金矿关系密切的银、砷、铅、锌和锑的5组元素含量再次进行提取,形成的数据集合命名为训练集2。

因为所给数据是一维的,不涉及到图片处理,所以网络选择Keras的一维卷积神经网络。

池化选择最大池化,因为处理非图像数据需要用最大池化来减小卷积层参数误差造成估计均值的偏移。

全连接层激活函数选择relu激活函数。

线性整流函数(linear rectification function),又称修正线性单元,对于进入神经元的来自上一层神经网络的输入向量,使用线性整流激活函数的神经元会输出至下一层神经元或作为整个神经网络的输出。

输出层为二分类,选用siqmoid激活函数。

标签分类的0和1是由测点所在地是否位于实际金矿地而定,位于金矿区内的点设标签为1,金矿区以外区域的点设标签为0。

定义损失函数来用于模型参数的估计,在训练完该卷积神经系统后会得到相应的损失函数。损失函数(loss function)或代价函数(cost function)是将随机事件或其有关随机变量的取值映射为非负实数,以表示该随机事件的“风险”或“损失”的函数。在应用中,损失函数通常作为学习准则与优化问题相联系,即通过最小化损失函数求解和评估模型。当一个模型完美时(虽然不存在),其误差为0;当模型存在问题时,误差不管是负值还是正值都偏离0,误差离0越近说明模型越好。

经过多次训练的调整,发现训练2 000轮的准确率函数与损失函数的结果能够快速收敛,所以将训练轮数设定为2 000轮。用上述参数进行训练后得到了卷积神经网络。图4给出了2组训练集的损失函数与准确率函数。

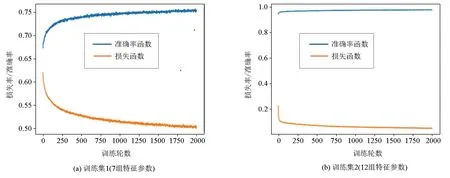
图4 训练后的准确率函数与损失函数

训练结果表明:

1)该网络训练次数越多得到的准确率越高,效果越好。

2)由于所选择的特征仅有7个,所以准确率仅有76%;增设5组特征重新进行训练,所得到的准确率函数达到了95%以上,损失函数也在0.1左右。由此说明在卷积神经网络的训练中,所选特征数据越多,其准确率会提高。

卷积神经网络的评价主要是根据准确率函数和损失函数来进行,损失函数越小,准确率越高,则该卷积神经网络的效果就越好。

4 验证集划分

首先进行验证。选择一块与网络训练使用区域大小相当的区域数据来进行验证,所选区域经度为121.3°～ 122.0°,纬度为37.0°～37.3°,经纬度均以0.02°为间隔来取点。验证集点位分布见图5。验证集的选取理由有2点:①验证集区域和训练集区域大小相差不多;②验证集区域的岩性和地质构造与训练集区域差别不大。

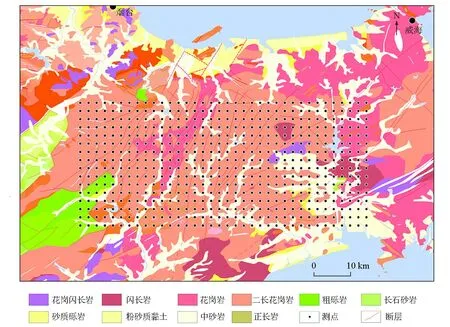
图5 验证集点位分布

验证集一共有577组数据。与提取训练集类似,将验证集每个测点的7组和12组特征数据分别提取出来,得到验证集1和验证集2,然后将其分别用对应卷积神经网络进行验证,得到每个测点对应的标签与存在金矿的概率。

为了验证网络的效果,将输出结果作等概率图,通过比较其中的高概率区是否与实际金矿位置吻合来验证网络的准确性(图6)。

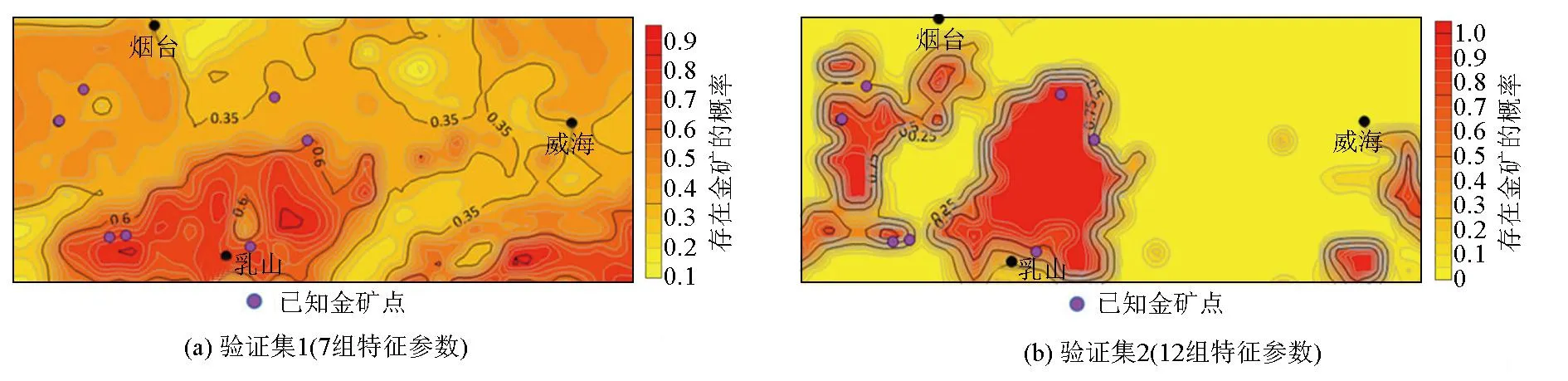
图6 验证集的输出等概率图

验证集1中中部呈现高概率的区域确实有已知金矿的存在,但仍然有已知金矿点处于0.4～0.5的低概率区域;在0.3～0.4概率区间也存在一个已知的金矿点。而验证集2相比于验证集1的测试结果更为理想,基本所有已知金矿都处于高于0.5的概率区域。这说明增加与金矿床产出相关的参数(化探元素异常)进行网络训练,得出的卷积神经网络会更好地预测金矿的存在。

验证集2中仍有少数几个实际金矿位置出现在预测概率只有0.25～0.5的区域,这可能是因为验证集所在的位置岩性不够复杂,略微单一,选取的特征之一的岩性数据重复较多,同时验证集的数据量并不多,缺少更为精确详细的数据;这些因素可能对所得结果产生了消极影响。图6b中东南部高概率反应区并没有金矿存在,卷积神经网络仍然存在改进的空间。

验证结束,所得结果较为理想,各项参数不再进行调试,直接应用到测试中。

5 测试集划分

图7给出了测试集的选取点位分布。选择该测试靶区的理由有以下几点:①该区域的岩性不单一,地形构造也多种多样,能提高所得结果的准确性;②该区域的已知金矿较多,得到的结果有利于直接用于对比;③该区域重、磁等资料较丰富,能得到较为准确的原始数据。

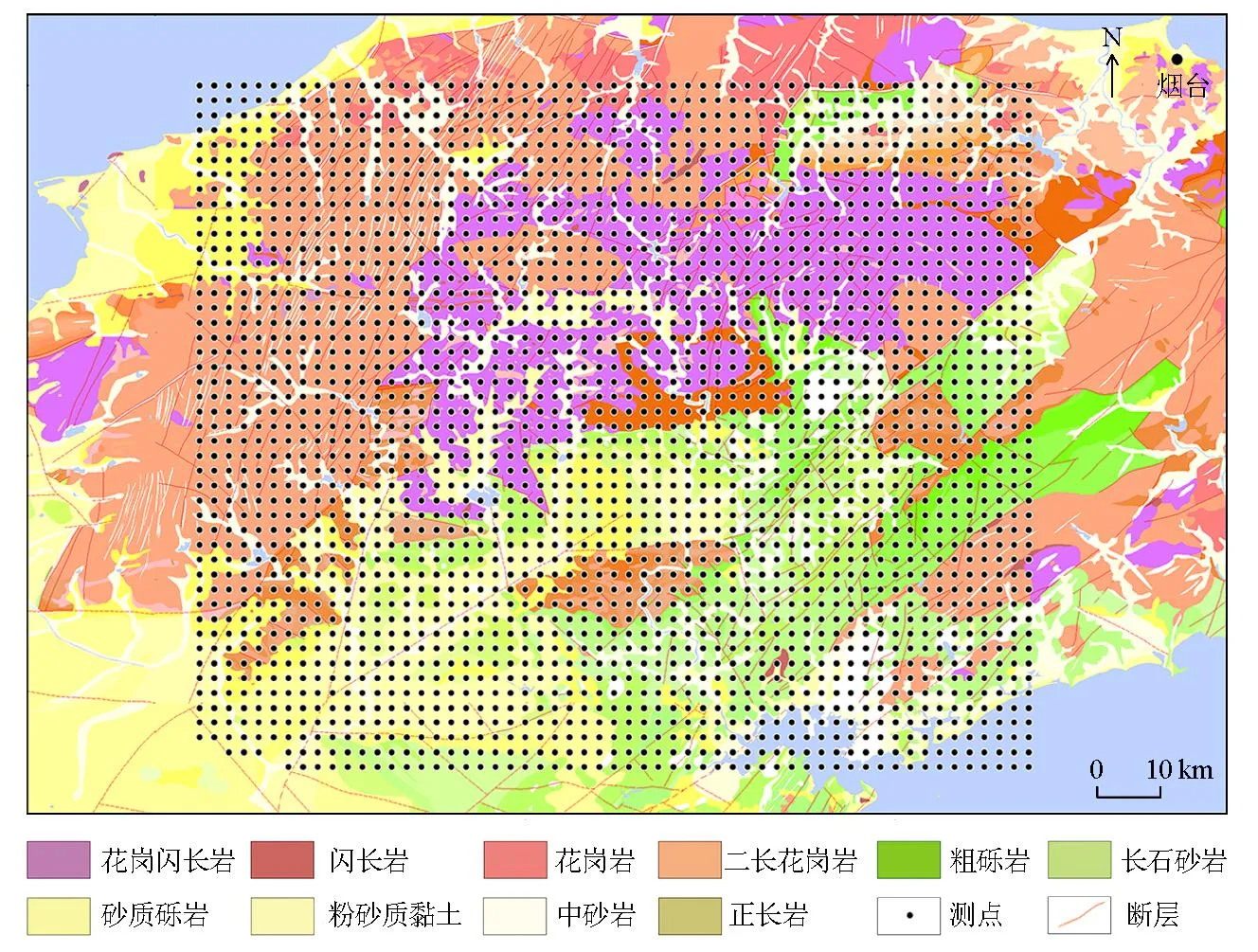
图7 实验测试集数据选取的点位分布

测点的选择是根据经纬度来划分的。选择经度范围为120.06°～121.18°,纬度范围为36.58°～37.50°,均以0.02°为间隔来取点。由于数据缺失和数据重复,所以舍弃了左下角与右下角的部分点位数据的提取。将测点整理成一个数据集,该数据集一共有2 814个测点。与验证集的提取相同,分别提取出测点的7组和12组特征数据得到测试集1与测试集2,然后将2个测试集分别用对应卷积神经网络进行测试,得到每个测点对应的标签与存在金矿的概率,做出等概率图(图8)。

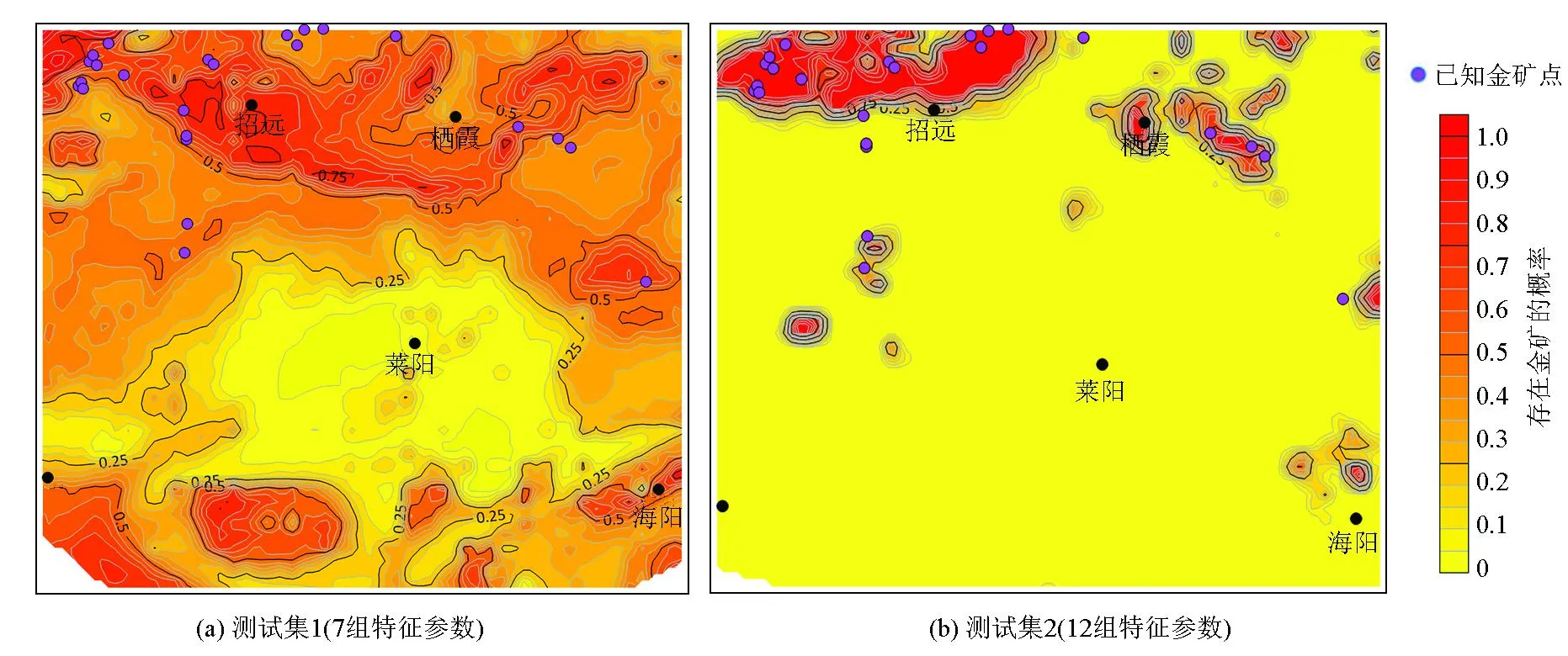
图8 测试集的输出等概率图

由图8可以看出,该网络的拟合结果良好,大多数金矿点都出现在图中50%以上的高概率区域,少数矿点出现在了低概率区域。东北部的实际金矿点与等概率图的高概率点基本吻合,得到了较好的结果,剩下的金矿点也基本上处于大于50%的区域,取得了较为良好的效果。测试集1中南部的高概率点在实地并没有金矿,这种结果的产生是由于卷积神经网络训练时所选用的特征较少,导致其准确率并不是很高。经过增设特征数据后,验证集南部区域的高概率反映消失,得到了更为准确的结果。

测试集1中化探异常仅利用了金元素含量,而与金矿关系密切的异常没有得到充分利用,这可能是导致部分预测结果不很理想的原因。在增设了跟金矿关系密切的相关元素化探数据后,得到了比较符合实际情况的结果,说明了卷积神经网络应用在金矿勘查方面是可行的。

6 结语

通过验证集与测试集的比较,测试集区域更为符合实际情况。因为测试集的数据几倍于训练集的数据,虽然该卷积神经网络选取的特征较少,但这种差异说明了深度学习在与目标输出相关的数据种类越多的情况下,所得到的结果就越为准确。因此,在利用卷积神经网络进行矿产勘查预测中,应尽量多地利用与矿产相关的地质、物化探等多专业数据来训练网络,以达到准确的预测效果。