基于可逆叠加变换的地滚波压制技术

吴 玉

(中国石油化工股份有限公司 石油物探技术研究院,江苏 南京 211103)

0 引言

地滚波是陆上地震资料中常见的一种干扰波类型,具有低频、低速、强能量、频散的特征,在单炮地震记录上呈扇形分布[1]。地滚波严重降低了陆上地震资料的品质,常规处理流程很难对其进行有效压制,残留的地滚波会在成像剖面上形成假象,干扰地震剖面(尤其是深层地震资料)的解释。有效压制地滚波是陆上资料处理的一个重要环节,是提高信噪比的重要手段。

工业界通常在采集阶段通过检波器组合压制地滚波[2]。然而,经过检波器组合后,还会有大量的地滚波残余,需要通过相应的处理技术进行压制。根据地滚波低频的特征,李文杰等[3]提出针对不同的炮检距选用不同的低切频高通滤波压制地滚波。利用地滚波低速的特征,石颖等[4]提出在十字交叉域通过三维FK滤波进行地滚波压制。地滚波存在速度频散,具有非稳态特征,通过小波变换可以在小波域设计一种时变、空变的自适应地滚波衰减方法,相比高通滤波,可以在衰减噪声的同时更好地保持反射波的振幅和相位信息[5-7]。通过小波变换可以把时间域地震数据变换到时间—尺度域,由于尺度缺乏物理含义,在尺度域设计滤波器比较困难,有学者提出通过S变换把地震数据变换到时频域进行噪声压制[8-10]。相比S变换,曲波变换由于其基函数具有多尺度和多方向的特征,更适合地震数据的表达,通过曲波变换对地震数据进行分解,在曲波域进行滤波是一种有效的地滚波压制技术[11-13]。

除了通过变换域滤波压制地滚波,还可以直接对地滚波进行建模,通过预测相减的方式对噪声进行衰减。Strobbia等[14]提出一种模型驱动的地滚波压制技术,通过频散曲线反演获取浅地表的横波速度模型,基于相移法合成噪声模型,通过匹配相减进行地滚波压制,取得了很好的压制效果[15-17]。但基于模型驱动的地滚波建模方案周期长,过程复杂,需要人工拾取频散曲线,耗时费力。Halliday等[18]提出通过基于数据驱动的地震干涉法地滚波建模技术,通过数据互相关预测噪声模型,借助匹配相减实现地滚波衰减[19-20]。

本文提出一种压制地滚波的新思路:在CMP域,反射波的同相轴为一系列双曲线,这些双曲线的顶点位于零偏移距位置,叠加速度能够唯一地表示这些双曲线的曲率。因此,可以通过叠加速度分析获取相对应的参数。对反射信号进行建模,求解对应的反问题获取零偏移距地震数据时,为了达到压制地滚波的目的,需要引入数据预条件算子消除地滚波对反演结果的影响。最后,由零偏移地震数据通过正演得到整个CMP剖面,由于正演算子不含地滚波的影响,最后得到的是干净的反射波数据,实现了衰减地滚波的目的。

1 可逆叠加变换反射波建模技术

1.1 正演算子

正演算子可以抽象表示为

d=Lm,

(1)

式中:d表示数据向量,是一个m维向量;m表示模型向量,是一个n维向量;L表示正演算子,是一个大小为m×n维的矩阵,作用是实现从数据域到模型域的映射。式(1)表示的是线性模型,正演算子不依赖于模型向量,但是正演算子的构建需要提供相应的参数信息,通常包括背景速度、子波、观测系统等信息。

本文研究的正问题是通过叠加道合成相应的CMP道集,与常规NMO叠加的映射方向相反,二者互为共轭转置关系,可以通过NMO叠加算子间接构建正演算子L。NMO叠加包括两个过程:动校正与叠加,可以抽象表示为

Lstack=SN,

(2)

式中:N表示动校正;S表示叠加算子。因此正演算子可以表示为

(3)

式中:T表示共轭转置。为了说明式(3)的含义,给出一个数值算例详细说明各项的具体作用。图1为层状介质模型,其中图1a表示层速度,图1b是根据层速度转化的均方根速度,在地层倾角比较小的情况下,均方根速度等于动校速度。图2a表示输入的叠加道,即模型向量m,将算子ST作用在图2a上,得到了零偏移距剖面结果(图2b)。将算子NT作用在图2b上,合成了CMP剖面(图3)。图2和图3的结果表明,提出的正演算子可以实现叠加道到CMP道集的映射。正演模型的建立是反演的基础,接下来探讨如何通过反演实现正演算子的可逆映射。

3)结合数据分析结果，向驾驶员提出预计停车60 s以上时采取熄火操作、低速行驶时以5 s间均匀加速为宜等策略，帮助驾驶员节约驾驶能耗.

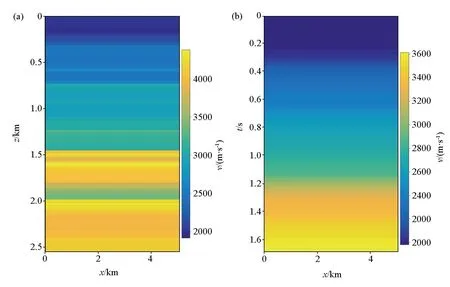
a—层速度;b—均方根速度a—layer velocity;b—RMS velocity

a—叠加道;b—零偏移距剖面a—stacked trace;b—zero offset section

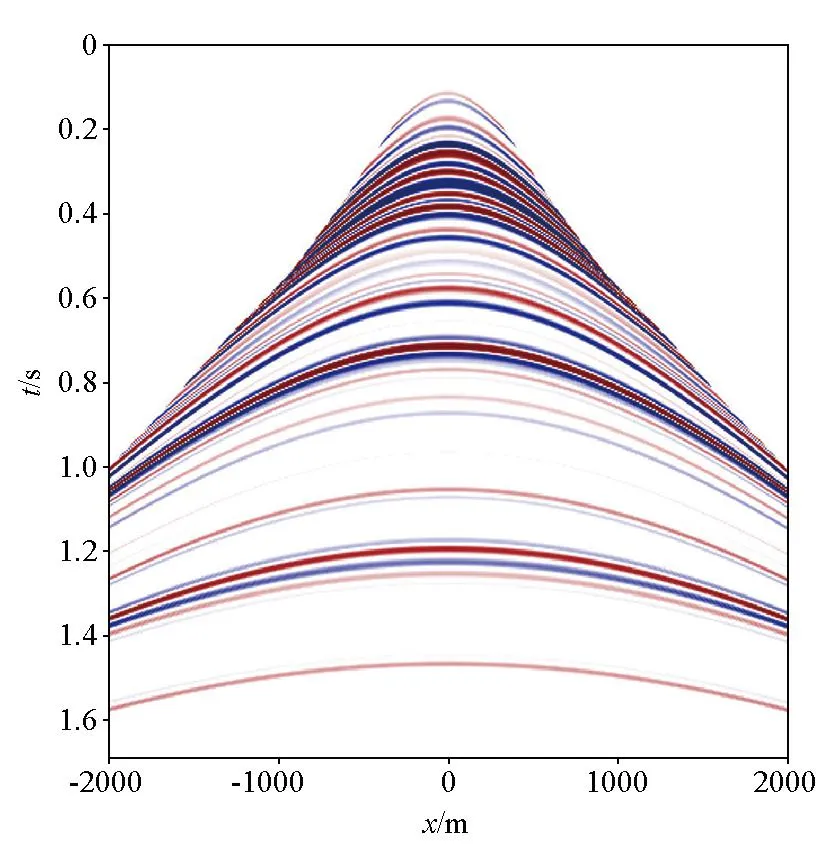
图3 CMP剖面

1.2 共轭算子

1.1节实现了叠加道到CMP道集的映射,但是,实际中经常求解的是对应的反问题,即如何通过CMP道集,估计相应的叠加道。反问题求解有两个关键:①共轭算子的构建;②最优化算法的实施。本节讨论共轭算子的构建,并进行相应的点积测试。正演算子的共轭就是常规的NMO叠加算子:

LT=SN

。

(4)

将图3的CMP道集进行动校正,结果见图4,经过动校正后,非零偏移距的走时得到校正,所有偏移距的走时对齐。在浅层,由于动校拉伸,对远偏移距的信号进行了切除。叠加算子S相对比较简单,对所有道求和即可。

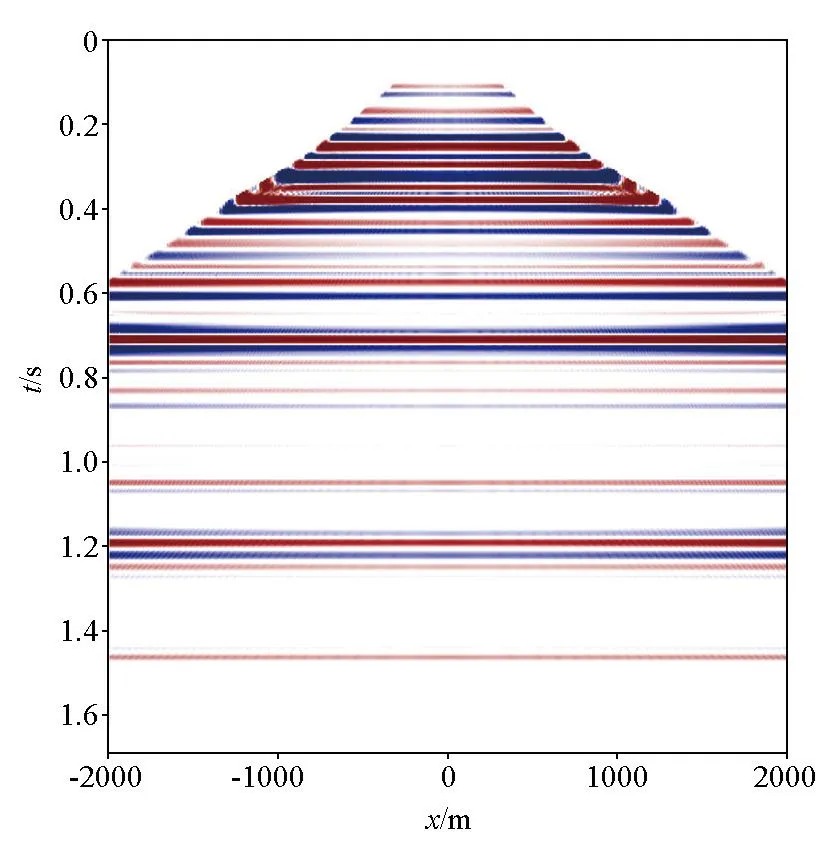
图4 动校后剖面

共轭算子的共轭性对后续反演求解的精度影响很大,需要通过点积测试验证共轭算子的精度。如果共轭算子是准确的,则下式成立:

〈Lm,Lm〉=〈m,LTLm〉,

(5)

式中:〈,〉表示两个向量的内积;m是一个随机的模型向量。输入一个随机的模型向量,使用本文方法计算的式(5)左边与右边的相对误差为10-16,在机器精度范围内,可以认为二者相等,表明本文提出的共轭算子可以满足反演对共轭性的要求。

1.3 可逆映射

为了实现模型域和数据域之间的可逆映射,需要把模型向量的估计表达为一个反演问题:

(6)

式中:‖‖2表示L2范数。通过最优化算法求解式(6),即可实现数据d和模型m之间的可逆映射。

(7)

共轭算法的收敛性可以通过残差曲线进行分析,对图3中的CMP道集进行反演,残差曲线见图5,共轭梯度法收敛很快,通常3～5次迭代即可收敛。

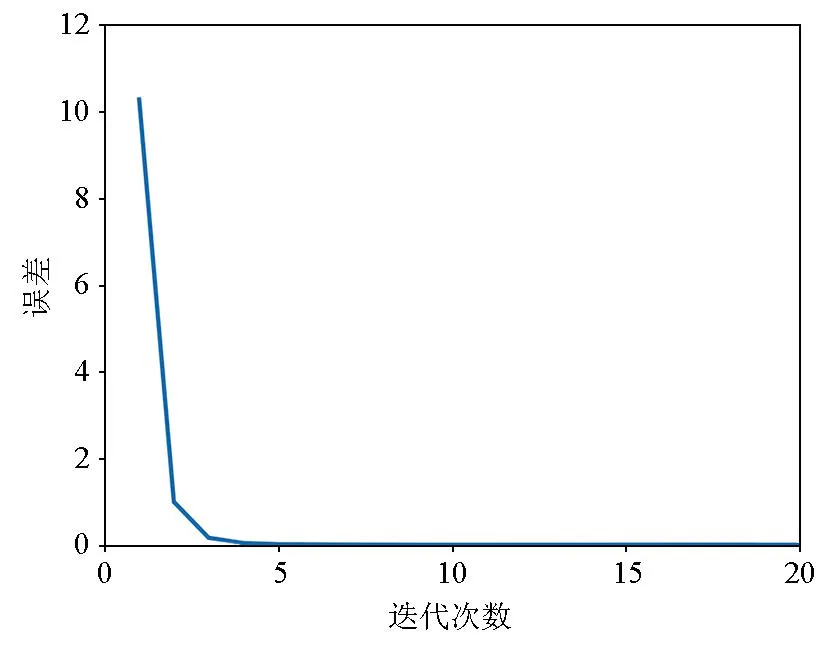
图5 残差曲线

2 基于反演的地滚波压制技术

2.1 信号噪声模型

在CMP域,地震数据可以表示为信号和噪声之和:

d=s+n,

(8)

式中:s表示反射波;n表示地滚波。图6是合成的含地滚波CMP道集,近偏移距地震数据被强振幅地滚波污染。由于地滚波低速的特征,在地震剖面上可以看到明显假频现象:同相轴出现锯齿现象。将地震数据变换到FK域,可以更明显看到假频的影响(图7),地滚波在奈奎斯特波数处发生卷绕。从图7可以看出,地滚波和有效信号在频带、波速、传播方向上存在重叠,这就决定了很难通过变换域+滤波的方法对地滚波进行压制。

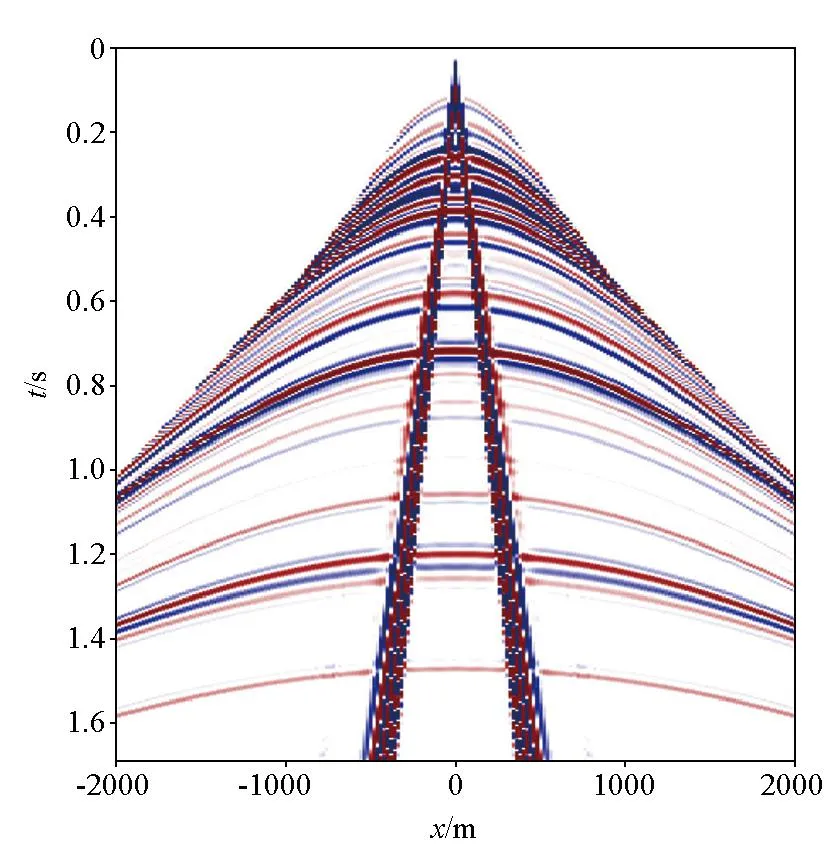
图6 含地滚波CMP道集

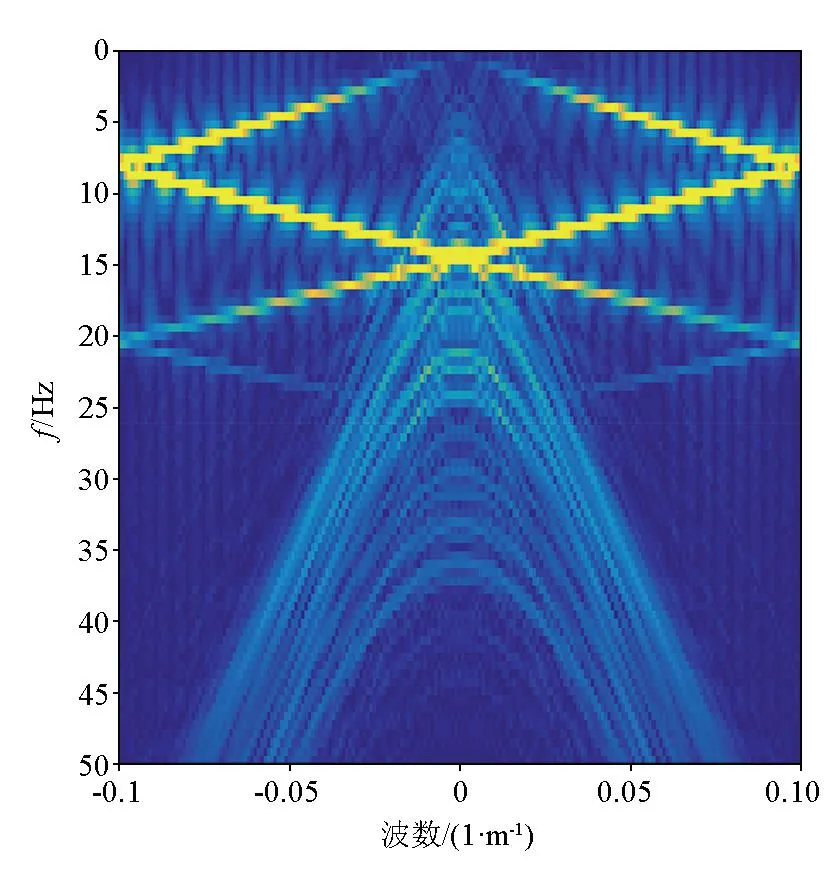
图7 含噪CMP道集的FK谱

2.2 数据预条件反演压制地滚波

如果引入额外的约束,对式(8)所示的信号模型很难进行处理。因此,根据前文的叙述,可以对反射信号进行建模约束,式(8)可以表示为

d=Lm+n,

(9)

通过对式(9)进行反演,可以得到模型m,进而可以通过正演得到反射波。但在实际中,由于地滚波n的存在,导致估计的模型m存在地滚波的干扰,很难达到理想的去噪效果。

由于地滚波的传播速度较低,能量被局限在近偏移距范围,见图6。在近偏移距信噪比较低,为了降低低信噪比数据对反射波估计的影响,设计一个MASK矩阵,降低这部分数据的权重,加权矩阵可以设置为

(10)

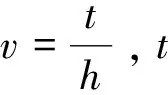
通过引入MASK矩阵作为数据预条件算子解决地滚波对反演的干扰,引入预条件后,式(9)变为

Td=TLm+Tn,

(11)

式中:T表示数据预条件算子,见图8,黄色表示1,蓝色表示0。由于Tn近似等于0,因此可以降低地滚波对反演结果的影响。

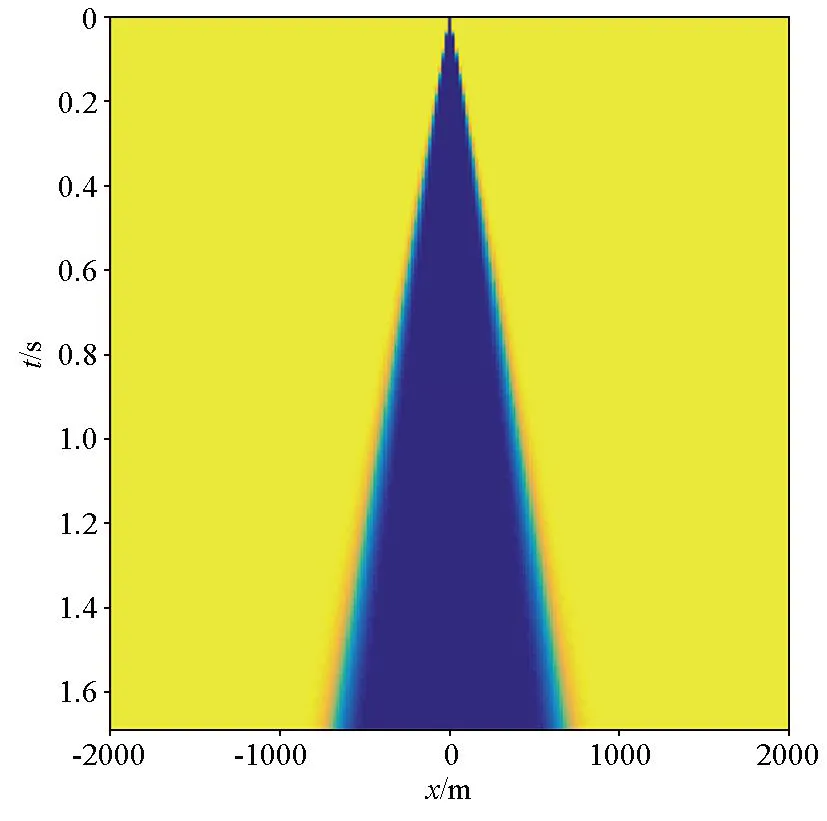
图8 数据预条件算子

图9是去噪结果,通过反演,完全可以把反射信号提取出来,在图9a看不到地滚波的残余,说明噪声得到了有效压制;图9b是去除的噪声,看不到有效信号的泄露,说明该方法具有很好的保幅性,在压制噪声过程中不会造成有效信号的损伤。

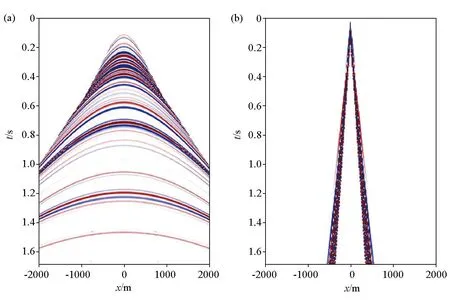
图9 去噪结果(a)和去除的噪声(b)

3 实际资料测试

为了测试本文算法在实际资料上的应用效果,选取西部某工区的陆上地震资料(图10)。通过对比,地滚波被有效压制,去除的噪声看不到有效信号的泄露,说明本文方法可以在压噪的同时尽可能保护有效信号,这非常有利于弱信号的保护。

a—实际数据;b—去噪结果;c—去除的噪声a—real data;b—denoised result;c—noise section

4 结论与认识

本文提出的基于可逆叠加算子的地滚波压制技术,算法噪声压制彻底,保幅性好,去掉的噪声几乎不含有效反射信号,数值算例证明了算法的有效性。但是,该方法基于层状介质假设,对于弱横向变化介质,噪声压制效果好,当速度存在比较大的横向变化,CMP叠加算子对反射波的建模能力降低,可能导致去噪效果变差,还需要结合实际资料开展进一步的研究工作。