基于全卷积残差收缩网络的地震波阻抗反演

2024-01-08王康刘彩云熊杰王永昌胡焕发康佳帅

物探与化探 2023年6期

王康,刘彩云,熊杰,王永昌,胡焕发,康佳帅

(1.长江大学电子信息学院,湖北荆州 434023; 2.长江大学信息与数学学院,湖北荆州 434023)

0 引言

地震波阻抗反演是高分辨率地震资料处理的最终表达形式[1],是在勘探与开发期间进行储层预测的一项关键技术。由于波阻抗能够较好地提供地层速度、密度以及孔隙度等参数信息,因此地震波阻抗反演在油藏描述、油气横向预测等研究工作中所起的作用越来越重要。地震反演的主要目的是从地震剖面反推出地下地层的波阻抗(或速度)的分布,从而进一步得到地下各层的岩性参数,如速度、密度、波阻抗、渗透率、孔隙度、砂泥岩百分比等[2]。以这些岩性参数为依据,进行储层预测和油藏描述,为建立储层的预测模型、地质模型和静态模型提供了简便方法。阻抗反演技术在过去40年里受到了广泛的关注,从直接反演到模型反演,从线性迭代反演到全局寻优。传统线性迭代方法在地震波阻抗反演中发挥了重要作用,如共轭梯度法、L1正则化反演等[3-4],以上线性反演方法对初始模型依赖性强、容易陷入局部最优,在一定程度上反演精度不高。随着波阻抗反演方法的发展,全局寻优反演方法随之兴起,模拟退火(simulated annealing,SA)、遗传算法(genetic algorithm,GA)、粒子群优化(particle swarm optimization,PSO)、蚁群优(ant colony optimization,ACO)等,因可以加入约束条件,不依赖初始模型并且易跳出局部值受到广泛关注[5-8]。但这些方法计算量较大,且难于用于高维反演问题。

近些年来,深度学习蓬勃发展,神经网络已被应用于解决一些地震反演问题,如地震数据插值、油气藏预测以及波形分类和识别等方面[9-11]。卷积神经网络(convolutional neural network,CNN)是最经典的深度网络结构,在各方面应用广泛,并且被成功地用于波阻抗反演,是基于深度学习的地震波阻抗反演中最常用的深度神经网络类型[12]。梁立锋等[13]提出在混合深度学习反演弹性阻抗基础上,探讨超参数对网络性能的影响,为深度学习地震反演超参数选取提供依据;Das等[14]使用两层全卷积神经网络(fully convolutional network,FCN)从地震图中获得波阻抗,并系统地测试了FCN的泛化能力。Puzyrev等[15]分别使用CNN、FCN和循环神经网络(recurrent neural network,RNN)从地震数据中预测速度模型,并证明了深度神经网络在地震反演中的适用性。Xu等[16]提出利用传统方法得到的粗略预测结果对U-net(一种特殊的FCN)进行预训练,然后通过测井数据对预训练后的U-net进行微调,用于油田数据预测。Guo等[17]使用双向长短期记忆RNN进行地震阻抗反演,从150口井的测井数据中生成了网络的训练样本。Wu等[18]提出了一种具有残差模块和两种注意力机制的残差注意网络,以提高地震波阻抗反演的模型精度。Wu等[19]利用Marmousi2模型合成地震数据,使用全卷积残差网络(fully convolutional residual network,FCRN)进行波阻抗反演,取得了很好的效果,但未进行抗噪能力分析。

Zhao等[20]提出的深度残差收缩网络用于机器故障检测,在残差网络的基础上加入软阈值函数和注意力机制,有效提高了抗噪性能。受此启发,本文对FCRN[19]改进,在其基础上也加入软阈值函数和注意力机制,提出了一种全卷积残差收缩网络(FCRSN-CW),以期让网络获得更好的抗噪声性能。

1 方法原理

1.1 FCRSN-CW反演流程

其主要流程共分为3个步骤(图1):

图1 FCRSN-CW地震波阻抗反演流程Fig.1 Flow chart of seismic impedance inversion using FCRSN-CW

1)通过正演得到合成地震数据,构成训练集;

2)从训练集中抽取数据训练FCRSN-CW网络;

3)训练完毕后,将地震数据输入FCRSN-CW网络,直接得到反演结果。

1.2 FCRSN-CW网络结构

为了分析残差块数量对反演结果的影响,确定最优的网络结构,我们对不同数量残差块的FCRSN-CW进行阻抗反演对比实验,分别计算其反演预测阻抗与真实阻抗的均方误差,实验结果如表1。

表1 不同残差块个数预测阻抗与真实阻抗的均方根误差Table 1 Mean square error of predicted impedance and true impedance by different residual blocks

由实验结果可知,当残差块个数设置为3的时候,网络的反演效果最好,所以本实验所采用的网络结构如上图2所示。

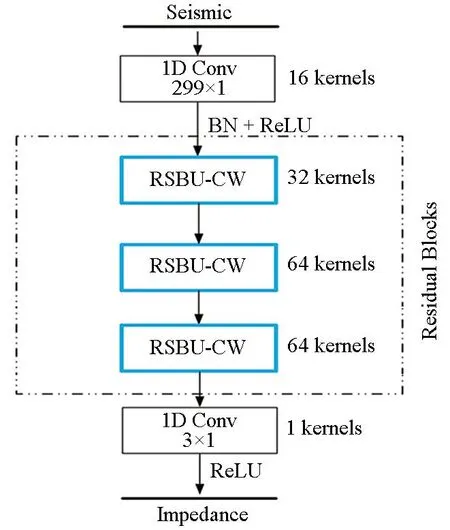
图2 全卷积残差收缩网络的网络结构Fig.2 Architecture of the FCRSN-CW

与Wu等[19]提出的FCRN不同的是,我们对FCRN中的残差块进行改进,如图2中蓝色框所示。全卷积残差收缩网络(FCRSN-CW)主要建立在3个部分的基础之上:深度残差网络、软阈值函数和注意力机制。相较于普通的卷积神经网络,深度残差网络采用跨层恒等路径的方式,缓解了深层网络的训练难度。深度残差网络的主干部分是由很多残差模块堆叠而成的,残差模块(residual building unit,RBU)是深度残差网络(ResNet)的基本组成部分。在Wu等[19]提出的FCRN中,一个残差模块包含两个批标准化(batch normalization,BN)、两个整流线性单元激活函数(rectifier linear unit activation function,ReLU)、两个卷积层(convolutional layer)和恒等映射(identity shortcut)。恒等映射是深度残差网络的核心贡献,在网络进行基于反向传播的模型训练时,其损失不仅能够通过卷积层进行逐层的反向传播,而且能够通过恒等映射进行更为方便的反向传播,从而更容易训练得到更优的模型,极大程度地降低了深度神经网络训练的难度。图2中的RSBU-CW代表的是改进后的残差模块,其结构如图3b所示,输入是通道数为C、宽度为W、高为1的特征图,K表示卷积层中卷积核的个数,在此图中K与输入特征图的通道数C相等。且如图所示中,输出特征图的尺寸和输入特征图的尺寸相等。图3a为改进前FCRN[19]中的残差模块。

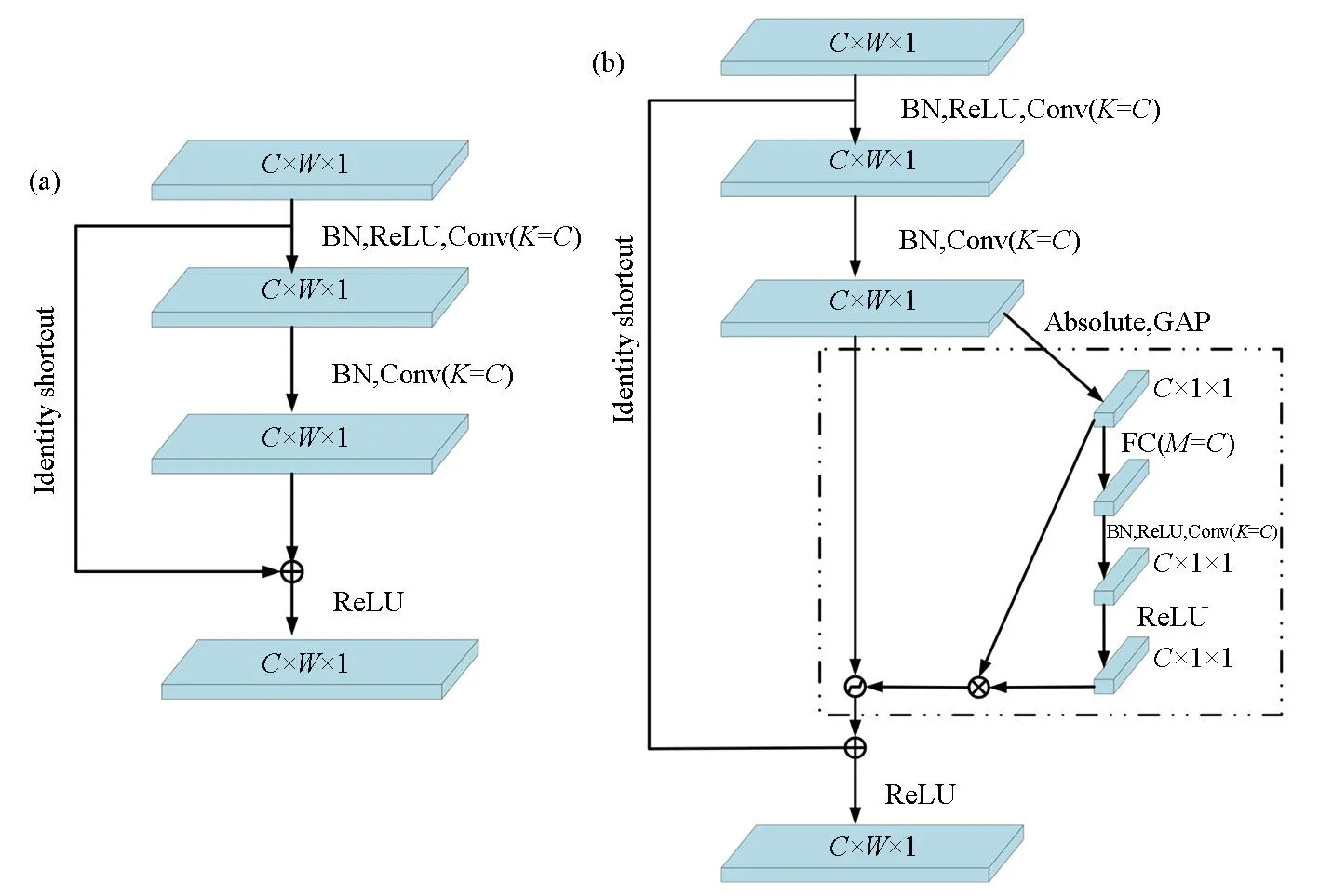
图3 改进前(a)、后(b)的残差模块(逐通道不同阈值)Fig.3 Residual building unit before(a) and after(b) improvement(different thresholds by channels)

本文使用的FCRSN-CW与ResNet类似,改进后的残差模块RSBU-CW是FCRSN-CW的基本组成部分,就是在深度残差网络的基础上增加了“注意力机制”和“软阈值化”。软阈值化是信号处理中常见的一种去噪方式,首先,我们需要设置一个正数阈值,该阈值不能太大,即不能大于输入数据绝对值的最大值,否则输出会全部为零。然后,软阈值函数会将绝对值低于这个阈值的输入数据设置为零,并且将绝对值大于这个阈值的输入数据也朝着零收缩。软阈值函数如下:

(1)

式中:x为输入;τ为阈值。其去噪的基本思想就是先对信号分解(卷积层的作用),然后对阈值内分解的所有信号进行过滤,最后将过滤后的信号重构。软阈值函数还有一个好处就是求导后梯度只有0和1,这样避免了梯度爆炸和梯度消失现象:

(2)

软阈值函数和ReLU激活函数有一定的相似之处,有利于深度学习算法训练时梯度的反向传播。阈值的选取对软阈值函数的结果有着直接的影响。

相较于FCRN[19]中的残差模块,图3中的残差模块里多了一个小型的子网络(如图3中虚线框部分)。而这个子网络的作用就是自适应地设置阈值,避免了人工设置阈值所需要的专业知识,且获得的阈值是一个向量,也就是特征图的每一个通道都对应着一个收缩阈值。此模块的阈值计算公式为:

τc=αc·average|xi,j,c|,

(3)

式中:τc是特征图的第c个通道的阈值;αc是缩放参数;i、j、c分别为特征图x的宽度、高度和通道数。改进后的残差模块能够更好地处理带噪声的数据,在对带噪声数据进行反演的时候能够给出更准确的反演结果。在本文实验中,RSBU-CW模块中第一个卷积层的卷积核大小为299×1,第二个卷积层的卷积核的大小为3×1。步幅设置为1,所有卷积层都使用零填充,使每个卷积层的输入和输出的大小保持相同。为了提高网络的非线性表达和加速网络收敛,我们选择ReLU作为激活函数。此外,我们应用批归一化(BN)来加速网络的训练。

为了更好地捕捉地震数据的低频特征,受Das等[14]的启发,设置卷积核大小与地震子波中心频率(30 Hz)对应的一个波长中的时间样本数量大小相当,可以让网络的学习曲线收敛得更好。所以FCRSN-CW的第一个卷积层有16个大小为299×1的卷积核,最后一个卷积层有1个大小为3×1的卷积核。中间堆叠的3个残差块的卷积核的个数分别为32、64、64,即分别对应了3个残差块的输出的通道数。

2 实验

2.1 合成数据

本文实验使用的波阻抗数据和合成地震数据成图如图4。

波阻抗数据是由Marmousi2模型纵波速度产生的,其数值等于介质密度ρ与波速v的乘积,其中介质密度被假定是恒定的。阻抗分布图如图4a所示,该剖面图由13 601条阻抗数据组成,每条阻抗有2 800个采样点,采样间隔为1 ms。然后通过正演计算得到合成地震数据集,具体计算方法就是先利用这些阻抗数据计算得到反射系数,计算公式如下:

(4)

式中:ri为反射系数r(t)的第i个采样点;Zi为阻抗Z(t)的第i个采样点。然后采用频率为30 Hz,相位为0°,幅度为-0.4～1 ms的雷克子波与反射系数进行卷积运算,得到的地震合成记录分布如图4b所示。

2.2 反演实验

从13 601道合成地震数据中随机取10 601道作为网络的训练集,1 500道作为验证集,1 500道作为测试集。网络的损失函数为均方误差函数(mse),定义为:

(5)

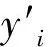
在本文实验中,我们在Marmousi2模型上训练和测试了FCRSN-CW。作为对比,Wu等[19]提出的FCRN也在相同的数据集上进行了训练和测试。

首先使用10 601道地震数据来训练网络。然后从1 500条验证集数据中随机抽取两道地震数据作为网络反演输入,这里取验证集的第650道和第1 250道,每道地震数据的大小为2800×1,然后对反演输出结果与真实阻抗进行比较。如图5a、b所示为Wu等[19]和FCRSN-CW输出的相应预测阻抗和真实阻抗的对比,其中红色线代表真实的阻抗,蓝色线和绿色线分别代表FCRSN-CW和FCRN预测的阻抗。图6a、b分别为FCRN和FCRSN-CW对所有地震数据反演得到的预测阻抗。图中标记处可以看到本文实验方法的反演结果要稍好一些。通过计算网络输出的预测阻抗和真实阻抗的均方误差值(FCRN为0.049 5,FCRSN-CW为0.000 2)发现FCRSN-CW对Marmousi2合成地震数据能取得非常不错的反演效果。

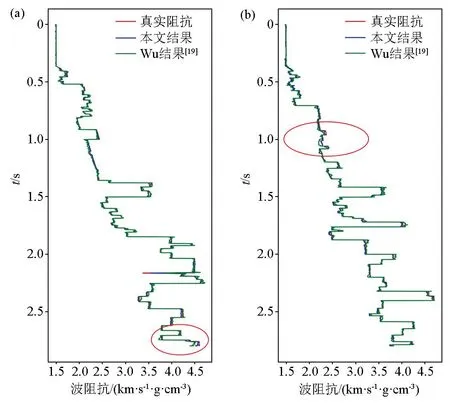
图5 FCRN[19]和FCRSN-CW分别对第650道(a)和第1250道(b)的反演结果Fig.5 Inversion results of No.650(a) and No.1250(b) by FCRN[19] and FCRSN-CW respectively

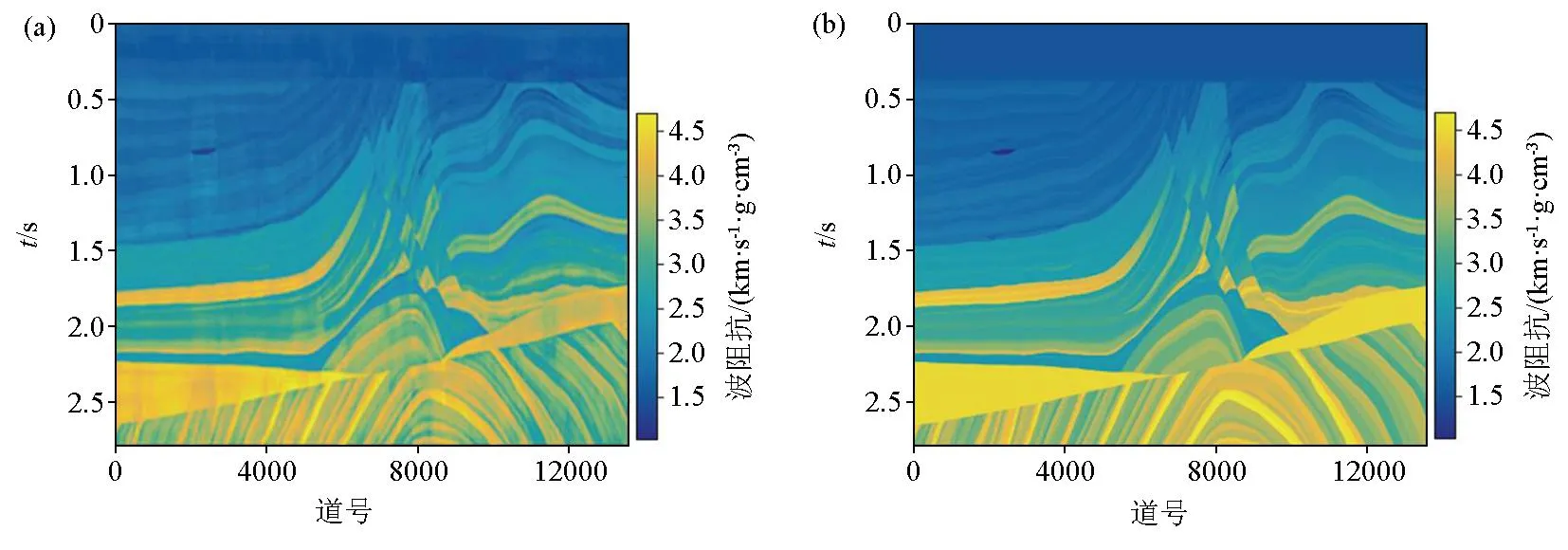
图6 FCRN[19](a)和FCRSN-CW(b)的预测阻抗Fig.6 Predictions of FCRN[19](a) and FCRSN-CW (b)

另外,实验测试了不同相位的子波对阻抗反演结果的影响。分别用不同相位的子波正演合成地震数据,然后进行反演,反演阻抗与真实阻抗的均方误差如表2所示。

表2 不同相位子波预测阻抗与真实阻抗的均方根误差Table 2 Mean square error of predicted impedance and true impedance by wavelet with different phases

由上表数据可知,当子波相位与训练集子波相位相同时(0°)反演效果最佳,两者不同时反演效果变差,其中,子波相位为30°时反演效果相对最差,子波相位为90°时反演效果相对最好。

在真实的环境中,地震道数据通常会带有不同程度的噪声,而这些噪声会直接影响网络的反演结果,因此抗噪能力分析是评估网络质量的重要步骤。本文通过对加噪地震数据的反演实验测试了FCRSN-CW的抗噪声性能。首先使用不加噪声的地震数据来训练网络,然后再给合成地震数据分别加上信噪比为35、25、15、5 dB的高斯噪声,与上面实验方法相同,从带噪声的验证集中随机取其中两道数据作为网络的输入,这里同样取第650道和第1 250道,观察其反演预测的阻抗与真实阻抗之间的差距。如图7a～h所示分别为信噪比在35、25、15、5 dB的高斯噪声环境下FCRN和FCRSN-CW输出的相应预测阻抗和真实阻抗的对比。由图可以看出在噪声环境下FCRSN-CW输出的预测阻抗是比FCRN要更接近于真实阻抗的。

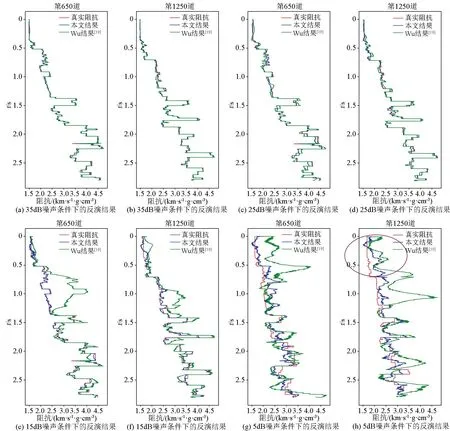
图7 带噪声数据的反演预测阻抗Fig.7 Predicted impedance from noisy data

图7a、b为网络在35 dB噪声条件下的反演结果,我们的结果和Wu等[19]的基本接近。图7c、d为网络在25 dB噪声条件下的反演结果,我们的结果要略优于Wu等[19]的结果。图7e、f为网络在15 dB噪声条件下的反演结果,可以看到,Wu等[19]的结果明显失真,与真实阻抗相差较大,而我们的结果与真实阻抗比较接近。图7g、h为网络在5 dB噪声条件下的反演结果,Wu等[19]的结果和我们的结果均出现失真,但我们的反演阻抗与真实阻抗的曲线趋势大体一致。从图7可以看出,在噪声较小时,本方法和Wu等[19]的反演效果相近,本方法略优;在噪声较大时,本方法的反演结果明显优于Wu[19]。

为定量分析本方法(FCRSN-CW)和Wu等[19]方法(FCRN)的反演效果,我们计算两者在不同噪声环境下反演结果的均方误差MSE,如表3所示。

表3 不同噪声强度下预测阻抗与真实阻抗的均方误差Table 3 Mean square error of predicted impedance and true impedance with different noise

以上实验结果表明:当信噪比小于等于5 dB时,噪声比较大,本方法反演结果明显变差。因此,用本方法处理实际资料的时候,应该尽量控制数据噪声的信噪比大于5 dB,以确保能得到较准确的反演结果。

在图7h中观察到第1 250道的浅层反演效果比深层的差,为了明确这是少数道的个别现象还是全区域的普遍现象,我们对全区域反演结果进行统计计算,将0～0.56 ms(占整条数据长度的1/5)范围内的阻抗数据划分为浅层数据,将0.56～2.80 ms(占整条数据长度的4/5)范围内的阻抗数据划分为深层数据,分别计算在不同噪声环境下反演得到的预测阻抗与真实阻抗在浅层和深层的相关度,计算皮尔逊相关系数(pearson correlation coefficient,PCC),结果如表4所示。

表4 预测阻抗与真实阻抗在浅层和深层的PCCTable 4 The predicted impedance is compared with thetrue impedance at shallow and deep PCC

由表4实验数据可知,理论模型对加噪地震数据反演得到的预测阻抗与真实阻抗在浅层的相关度是要低于在深层的相关度,而且噪声越大,这种差异就越明显。

3 实测资料处理

使用了挪威近海的Volve实测数据来检验该方法的反演效果,目的是使用本文提出的FCRSN-CW方法来预测Volve数据集中部分地震数据对应的阻抗(图8)。由于只有一条测井数据,数据量非常有限,所以需要根据测井数据的特性来增加数据集,用以网络的训练。其中地震子波可以通过对测井数据估计得到,这里采用的是中心频率为20 Hz的零相位雷克子波。然后根据测井阻抗的特性使用序贯高斯模拟来生成具有统计特性的波阻抗数据,再将模拟波阻抗数据通过计算得到反射系数,最后将反射系数与地震子波进行正演卷积运算,就可以得到标记的波阻抗—地震道数据对。这些扩充得到的数据对就可作为网络的训练集数据。

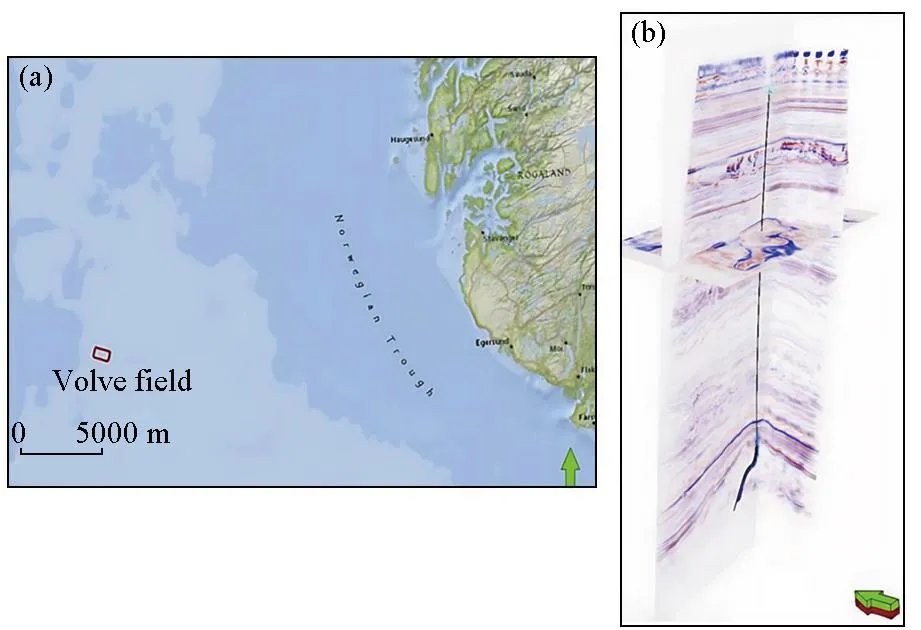
图8 Volve油田的位置(a)和来自Volve油田的地震数据和测井数据(b)Fig.8 Location of the Volve oil field(a),seismic data and well log data from the Volve oil field(b)

通过上述方法得到一个三维的数据集,大小为151×151×160,其中每道地震数据的长度为160。在划分数据集的时候,训练集大小为75×151×160,验证集和测试集大小均为15×151×160,相当于训练集有11 325道地震数据,验证集、测试集各有2 265道地震数据。由于地震数据的长度只有160,所以将原网络中卷积核的大小换成80×1,batch size设置为15,同样训练50次。这里将通过测井阻抗计算得到的反射系数与地震子波进行卷积运算,然后使用训练好的网络模型对得到的地震数据进行反演,图9显示了预测阻抗与真实测井阻抗的比较。由图可看出预测的阻抗与真实的测井阻抗匹配度较高,计算其相关度为94.3%。另外我们实验测试了不同相位、频率的子波对上述实际资料阻抗反演结果的影响。分别用不同相位、频率的子波正演合成地震数据,然后训练网络进行反演,反演阻抗与真实测井阻抗的皮尔逊相关系数(PCC)如表5所示。

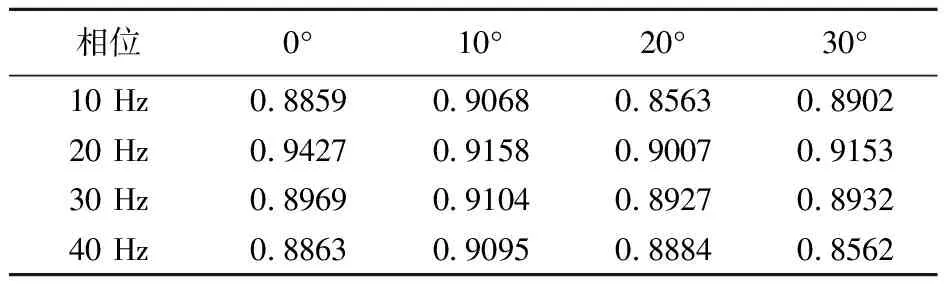
表5 不同相位和频率子波预测阻抗与真实阻抗的PCCTable 5 PCC of predicted impedance and true impedance by wavelet with different phases and frequencies

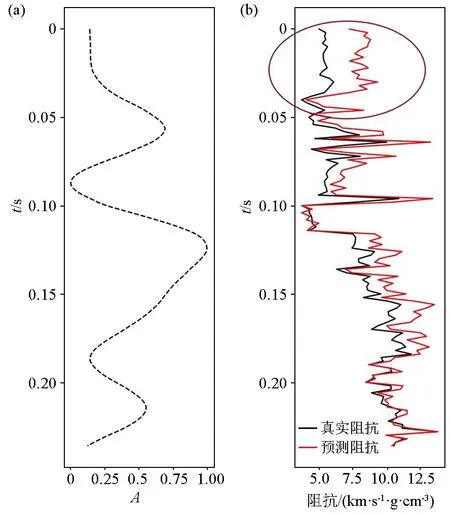
图9 输入地震数据(a)以及测井阻抗和预测阻抗(b)Fig.9 Input seismic data along well(a) and corresponding true and prediction impedance(b)

由表5数据可知,当子波频率为20 Hz时的反演效果要优于子波频率为其他数值时的反演效果,其中,当子波频率为20 Hz、子波相位为0°时的反演效果最佳。因此,针对Volve实测数据的地震波阻抗反演,我们采用中心频率为20 Hz的零相位雷克子波来进行反演实验。另外,当实际资料只有地震数据时,需要根据地震数据的特性进行地震子波提取,提取的具体方法要根据具体数据和研究目的进行选择,以确保提取到的地震子波能够准确反映地下介质结构的特点。

值得指出的是,在图9中虽然预测的阻抗与真实的测井阻抗匹配度较高,但是预测曲线在浅层的误差大,在深层的误差相对较小,这与上文理论模型反演带噪声数据时浅层反演效果比深层的差这一现象一致。至于为什么浅层的相关度会低于深层的相关度这一问题还有待进一步地研究论证。