基于新奥法隧道施工中隧道受力数值分析

周林政

（江西省水利水电建设集团有限公司，江西 南昌 330200）

隧道在施工过程中，隧道围岩的稳定性存在不可控的风险，隧道围岩稳定性与受力变形分析是2个十分重要的问题，合理控制围岩变形是防止隧道发生局部坍塌的重要措施[1，2]。衬砌是防止围岩变形或坍塌的常用支护结构之一，能够支持和维护隧道的长期稳定和耐久性。然而受施工技术和地质环境的影响，部分工程衬砌会出现变形沉降，严重威胁隧道安全运行，因此分析其衬砌受力变化具有重要意义[3]。

郭根发[4]采用Peck 公式计算和FLAC3D 软件模拟2种方法分析了上海某地铁隧道衬砌内力及沉降变形；王淑娟[5]采用数值模拟建立了详细的三维数值模型，研究了跨断层深海隧道衬砌变形规律及加固措施；傅鹤林等[6]以国内在建特长隧道为工程背景，对加固圈的厚度、泊松比、弹性模量、衬砌半径、衬砌厚度5个参数进行数值模拟分析；刘登新[7]通过有限元数值模拟软件建立模型，在原有15°接缝倾角的基础上设置0、9°和18°作为3组工况，研究分析接缝倾斜角度对水工隧道衬砌管片受力的影响；雷晓丹等[8]通过山西某高速公路隧道病害区域的现场监测发现，衬砌变形的整体特征为底部上翘、边墙外扩、拱圈下沉；范一鸣等[9]采用有限元法建立能够考虑衬砌块与块、环与环、衬砌与周围土体相互作用的精细化"梁-弹簧"数值计算模型。

新奥法是当前隧道工程较为常见的一种掘进方法，它将锚杆和喷射混凝土组合在一起作为主要支护手段，已在世界许多国家地下工程中得到广泛应用。本文为探讨隧道在新奥法工艺下的变形特征，以某隧道为例研究了衬砌安装、锚杆支护系统安装以及隧道掘进对隧道变形的影响，得到了其弯矩和应力的变化规律，研究结果对了解新奥法施工过程隧道衬砌和整体变形规律具有借鉴意义。

1 工程概况

本次研究的隧道长20 005 m，设计为2 座单线隧道，除出口段线路位于半径为1 300 m曲线上，右、左线缓和曲线伸入隧道58.76、137.19 m 外，其余地段均位于直线上，线间距41 m；2 座隧道线路纵坡相同，右线隧道较左线隧道高0.52～0.62 m。隧道进口右线轨面设计高程2 354.8 m，交通便利，隧道最大埋深1 100 m。本段线路位于中温带干旱气候区，春季多风，少雨干旱；夏季酷热，降水增多；秋季凉爽，降温较快；冬季寒冷，干旱少雪；气候垂直分带性明显，日温差大，阴雨风雪冰雹天气多变，冰冻时间长。本段年平均气温-0.2～4.1°C，绝对最高气温25.1～33.7°C、最低气温-27.0～-31.6°C；多年平均降水量345.8～400.4 mm，最大降水量542.7 mm；多年平均蒸发量1 538～1 803.6 mm。

2 数值理论

在使用新奥法施工隧道的过程中，首先通过暂时的内衬结构将隧道的上半部固定，同时进行与其下半部挖掘平行的作业，如图1所示。

图1 新奥法施工隧道

然而，隧道因为掘进而导致的截面面积的变化和临时衬砌的安装会改变整个隧道岩体与支护体系的应力-应变状态，因此对每个开挖工期进行一系列隧道稳定性分析十分重要。

采用基于变分公式的有限元方法对隧道的变形进行了分析，其中物体的变形势和外力势的方程通过位移函数表示，使用柯西方程描述：

式中：u，v，w分别为单元节点的位移（m）；μ为泊松比；G为剪切模量（Pa）；V表示单元的体积（m3）。

物体外力势可表示为：

式中：Qx，Qy，Qz表示体积在x，y，z轴上的投影（m3）；Px，Py，Pz表示计算区域Ω（m2）上的力在x，y，z轴上的投影（N）。

物体变形势可以以矩阵形式表示为：

式中：[K]为刚度矩阵（N/m）；{ }UT和{ }U分别为单元节点位移的转置和非转置向量（m）。

3 模型建立

隧道模型被假设为均匀厚度、各向同性、线性弹性材料。隧道有限元模型，如图2 所示。由于模型包括一整套支护体系，因此先将临时衬砌单元安装在拱顶中（见图3（a）），然后安装锚杆支护系统（见图3（b）），最后设置开挖区域（见图3（c））。

图2 初始“临时衬砌-隧道”有限元模型

为了提高计算的准确性和反映“临时衬砌-周围岩体”系统现场相互作用的真实性，在工作区周围创建了一个40 m×40 m 的岩体，并用0.5 m×0.5 m 的有限单元离散。岩石的物理力学参数如下：弹性模量为210 000 kN，泊松比为0.2，容重为22 kN/m3。此外，临时衬砌采用H 梁形式，带平行翼缘，锚（采用10 kN 的预应力）直径为20 mm、长度为4 m、最大允许断裂力为80 kN。

4 数值结果分析

隧道在支护系统建立及开挖过程中的弯矩变化过程，如图4所示。

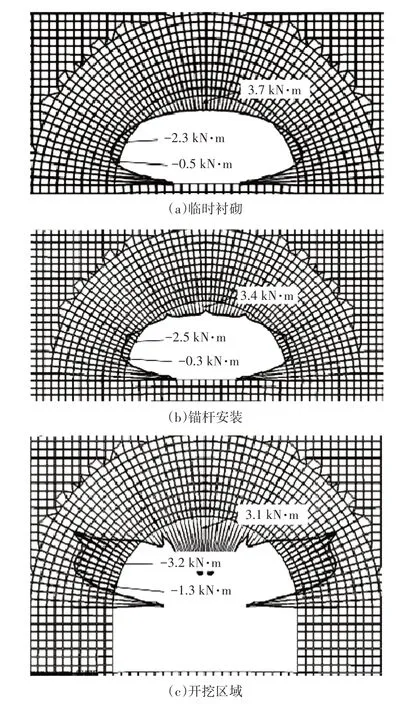
图4 隧道在支护系统建立及开挖过程中的弯矩变化

从图4（a）可以看出，当隧道只安装临时衬砌单元时，拱顶的弯矩最大为3.7 kN·m，而隧道左壁出现了负弯矩，监测点弯矩为-2.3、-0.5 kN·m。因此，隧道衬砌安装完成后，出现了明显的不均匀变形。这是由于衬砌受到不同方向上的作用力而引起的弯矩。总体而言，无论是正弯矩还是负弯矩，都是为了克服衬砌自身产生的弯矩。这样的设计不仅能够减轻荷载对衬砌造成的损害，同时有助于确保隧道的安全性。但过大的弯矩会引发衬砌产生裂缝，因此在安装衬砌时应该合理设计弯矩范围。从图4（b）可以看出，当隧道安装锚杆后，拱顶弯矩由原来的3.7 kN·m 降低至3.4 kN·m，而侧壁弯矩绝对值相比原来减少0.2 kN·m，表明隧道拱顶和侧壁的弯矩变化不大。从图4（c）可以看出，当隧道开始掘进下部预留岩体时，隧道3处监测点的弯矩出现较大变化，拱顶弯矩减少到3.1 kN·m，而侧壁弯矩绝对值分别增加到3.2、1.3 kN·m，说明当隧道开始掘进下部预留岩体时会导致隧道侧壁发生挤压，因此该施工阶段需要对侧壁的内力变化进行密切监测以防止隧道垮塌。

主应力是反映结构应力状态的重要指标，隧道在支护系统建立及开挖过程中的主应力变化过程如图5所示。

图5 隧道在支护系统建立及开挖过程中的主应力变化

从图5（a）可以看出，当隧道只安装临时衬砌单元时，拱顶的主应力为196 kN，主要表现为受拉状态，而隧道侧壁主应力分别为-1 022、-1 137 kN，表现为受压状态，因此隧道内部变形不均匀，与上述根据弯矩得出的结论一致。从图5（b）可以看出，当隧道安装锚杆后，拱顶应力并未发生明显变化，同时侧壁应力也只出现了微小变化。从图5（c）可以看出，当隧道开始掘进下部预留岩体时，隧道3 处监测点的正应力出现较大变化，此时拱顶正应力增加至211 kN，而侧壁正应力分别变为-873、-858 kN，说明当隧道开始掘进时，隧道拱顶的拉应力逐渐增大，而侧壁的压应力也逐渐减少，总体上应力相比衬砌和锚杆安装时有明显突变趋势，隧道出现严重变形的风险增大，需要采取监测和加固措施。

5 结论

本文为探讨隧道在新奥法工艺下的变形特征，以某隧道为例研究了衬砌安装、锚杆支护系统安装以及隧道掘进对隧道变形的影响，得到了其弯矩和应力的变化规律。研究结果表明，当隧道只安装临时衬砌单元时，拱顶的弯矩最大，隧道衬砌安装完成后出现了明显的不均匀变形。这是由于衬砌受到不同方向上的作用力而引起的弯矩。而当隧道安装锚杆后，隧道拱顶和侧壁的弯矩变化不大。相比前两步施工过程，当隧道开始掘进下部预留岩体时，会导致隧道侧壁发生挤压，这一施工规律在考虑主应力时同样有相似表现，因此该施工阶段需要对侧壁的内力变化进行密切监测以防止隧道垮塌。