黏土水泥浆流变本构模型及其时变特性研究

2024-01-08田庆浩

金属矿山 2023年12期

田庆浩

(1.北京中煤矿山工程有限公司,北京100013;2.矿山深井建设技术国家工程研究中心,北京100013)

注浆浆液始终是注浆技术的核心研究内容之一,随着世界上各个国家尤其是中国地下工程建设的飞速发展,注浆法的应用变得愈加广泛,国内外科研工作者在注浆扩散理论方面也做了不少的研究工作。早期的研究者从流体力学方面分析了单液水泥浆在裂隙中的扩散方程,随着技术的进步,近年来有不少学者采用理论推导、数值模拟或模型试验的方法,对注浆扩散规律进行了各种研究,对注浆理论的发展和现场起到积极的作用[1-3]。李术才等[4]研究了水泥-水玻璃浆液和改性水泥浆液2种浆液黏度的时变特性;何涛等[5]则研究了生物胶、缓凝剂等在恒定剪切速率与变化剪切速率下对浆液黏度的影响;阮文军等[6]则通过室内试验分析发现,不同水灰比的水泥浆液分属3种不同流型。

针对各类黏土水泥类浆液的流变性能也有学者进行了研究,郑晨等[7]通过室内试验对黏土-水泥浆在不同温度下的黏度及凝结时间的变化规律进行了研究;王星华[8-9]认为黏土-水泥浆浆液是带屈服值的假塑性流体,本构模型符合改进的双曲模型,但未考虑剪切速率及时间因素的影响;刘杰等[10]通过流变仪对层流状态下不同配比的黏土水泥浆的流变参数进行了试验研究,同样也未考虑时间因素的影响。上述3篇文献所研究黏土水泥浆未添加凝结剂,由黏土及水泥组成。韩春雨等[11]针对添加水泥及水玻璃的黏土水泥浆进行了本构关系试验,认为其为宾汉流体,但对于不同配比黏土水泥浆的流型并未进行详细的研究。

黏土水泥浆是当前注浆工程中应用最为广泛的注浆材料之一,由黏土浆及少量水泥、水玻璃组成。该浆液具有性价比高、可注性好、耐久性及堵水效果好等优点,在井筒预注浆、地面区域治理等众多领域得到了广泛的应用[12-14]。注浆是一个持续的过程,浆液的本构关系及流变性则是指导研究浆液扩散规律的重要基础条件,但针对黏土水泥浆的研究仍较少且多未考虑时间因素的影响。探究浆液的本构关系及模型参数随时间的变化规律对于研究浆液性质以及浆液在裂隙扩散的过程具有重要意义[15-18]。

1 黏土水泥浆本构模型试验

流变特性及流动规律的研究是浆液研究最为重要的问题之一,而本构方程的建立和流变参数的确定更是研究流体流动和流变特性的基础。目前国内外学者提出了很多本构模型,但能够准确描述黏土水泥浆的模型还有待研究探索,故本研究设计本构试验探究能够准确描述黏土水泥浆的本构模型。

1.1 试验配比设计

首先根据现场施工经验选取4种常用配比,如表1所示。这4种配比浆液由稀至稠分布均匀,能够覆盖常用配比浆液,充分体现黏土水泥浆浆液特性。

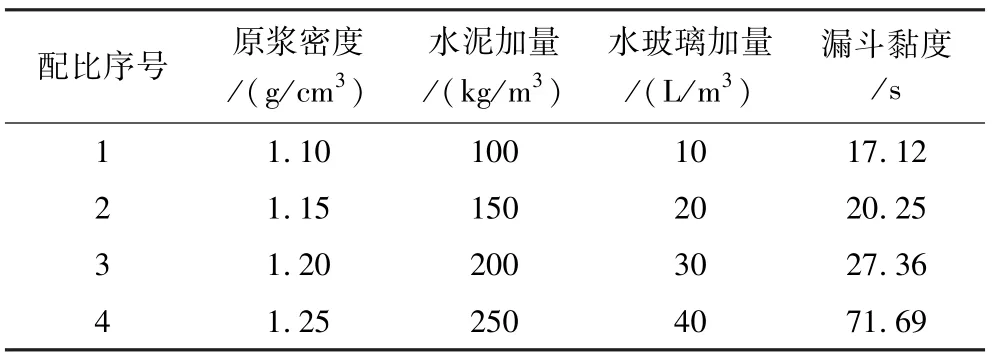
表1 本构试验配比Table 1 Constitutive test ratio

1.2 试验材料

1.2.1 黏土

黏土取自施工项目现场,并经实验室造浆除砂(含砂量小于3%)后用于室内试验,黏土成分及性能分析结果如表2所示。

表2 试验用黏土成分及性能分析结果Table 2 Test clay composition and performance analysis results

1.2.2 水泥

水泥为中联集团生产的基准水泥,水泥标准符合GB 8076-2008,产品型号为P·I 42.5硅酸盐水泥,并做防潮保存,主要成分检验结果如表3所示。

表3 试验用水泥主要成分组成Table 3 Main composition of cement for test

1.2.3 水玻璃

水玻璃为钠质水玻璃,浓度37°Bé,密度1.338 g/cm3。

1.3 试验步骤

按要求配置好各配比的黏土水泥浆液,通过旋转黏度计测试每个档位的流变数据,从读数盘读取对应的数据参数,经过对该参数进行计算处理,得到其对应的剪切应力;然后根据该实验结果绘制-τ曲线,并进行拟合处理,确定各配比浆液的本构模型。

本研究将利用Origin数据分析功能中的曲线拟合功能,利用宾汉流型、幂律流型及H-B屈服假塑性流型3种非牛顿流变本构模型进行数据拟合回归分析,对比评价不同流变本构方程拟合效果,从而确定黏土水泥浆的本构模型。其中,宾汉流体本构方程可表示为τ=τ0+;幂律流体方程表示为τ=;HB模型为τ=τ0+。各式中τ为剪切应力,τ0为屈服应力,μ为塑性黏度,K为稠度指数,为剪切速率,n为幂律指数。

拟合效果评价采用调整相关系数平方Adj.R2以及残差平方和RSS2个参数进行分析。其中Adj.R2称为调整相关系数平方,该参数的数值越靠近1则表示相互间的紧密程度越高;RSS称作残差平方和,RSS的值越小,就可以认为该组数据的相关程度越好。

1.4 本构模型试验结果分析

分析配比1～配比4浆液拟合数据及拟合参数,如图1、表4、图2所示,可以发现宾汉流型及H-B屈服假塑性流体能够准确描述黏土水泥浆的流变本构方程,幂律流体拟合效果均有所欠缺。又因为,宾汉流体的本构方程为线性方程,而H-B屈服假塑性流型的本构方程为幂指数型函数,故综合拟合效果并从考虑简化计算的角度,可以认为4种配比黏土水泥浆模型符合宾汉流型。

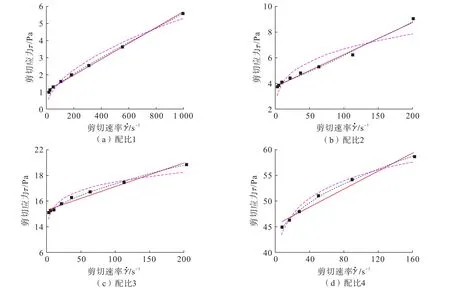
图1 配比1～4浆液流变拟合曲线对比Fig.1 Comparison of slurry rheological fitting curves of ratio 1～4

图2 配比1～4拟合参数分布Fig.2 Ratio 1～4 fitting parameter distribution

表4 配比1～4本构模型拟合结果Table 4 Fitting results of ratio 1～4 constitutive models

2 黏土水泥浆裂隙层流扩散理论分析

前文通过试验分析认为黏土水泥浆的本构模型符合宾汉模式,本构关系可以用方程τ=τ0+来表示。因此,本节便以宾汉流型为基础,推导黏土水泥浆裂隙层流注浆压力与扩散距离间函数关系。

2.1 裂隙模型

宾汉流体在裂隙层流时,假设浆液沿x轴方向流动,扩散距离用L表示,设y方向的裂隙开度为b,层流流核区高度为2y0,如图3所示。

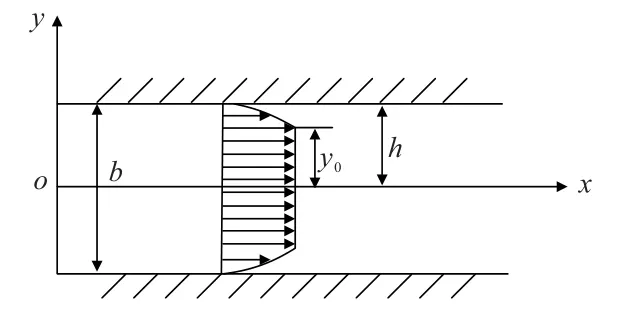
图3 裂隙层流示意Fig.3 Schematic of fracture laminar flow

2.2 裂隙扩散规律理论分析

令u为流速,ρ为流体密度,τ为附加应力,P为压强,fx为x方向的质量力。浆液在裂隙中流动的N-S运动方程:

不可压缩流体的连续性方程:

法向应力协调方程:

对于单向单裂隙模型,因裂隙y方向宽度远大于裂隙开度,故忽略y方向边界对于流体运动的影响,uy=uz=0;所以:

由连续方程,并根据单向流动条件,可知:

由于定常流动条件,所以:

对于宾汉流体浆液粘度粘滞性的影响远大于惯性的影响,假设裂隙x方向为相对地面水平方向,故忽略质量力fx影响,则fx=0。简化得到运动方程:

积分可得:

式中,τw为侧壁处的剪应力;ΔP为压差。

在不考虑时变特性条件下,浆液的本构关系可以表示为

则

由式(5)条件,代入式(7),更换积分变量可得:

该式便为黏性流体流速分布方程。

根据式(5)知,侧壁处浆液切应力最大,且当切应力τ小于屈服应力τ0区域内,浆液不流动,此时浆液流速便为0。因此,浆液产生流动的前提是τw＞τ0,即

屈服应力发生在固液两相的相互接触面处,故代入边界条件y=y0时,τ=τ0。根据侧壁处边界条件,y=h,u=0,代入式(5),可得流核高度:

可见,流核区高度与浆液压差、屈服应力及扩散距离等相关。

在浆液所承受的注浆压力恰好达到屈服应力开始流动时,此刻压力差表示为ΔP0,则

对比式(5)、式(9)及式(10),可以得到:

根据前文研究,黏土水泥浆符合宾汉模型,本构方程可以表示为

根据式(8)可得浆液梯速区流速:

代入式(5),整理可得:

对于流核区流速,将y=y0,代入式(13)可得:

根据对称性原则对截面(-h,h)区域,即整个截面梯速区及流核区积分,可求得截面均速:

计算得:

简化方程中高阶项可以得到:

又针对一展度为a的矩形裂隙,在恒定注浆量q注浆过程中,浆液在裂隙则保持恒定流速。因此,可以求得截面流速:

联立式(16)、式(17),解该联立方程,并将式(9)代入,可以得到压力差与扩散距离的函数关系式:

通过分析式(18),可以发现黏土水泥浆浆液扩散过程中,进出口压力差ΔP除了受裂隙大小以及浆液扩散距离L影响外,还与屈服应力τ0及塑性粘度μ密切相关,因此有必要进一步研究2个参数对浆液本构关系及扩散规律的影响。

3 黏土水泥浆本构模型参数时变特性试验

通过试验及理论分析可知,黏土水泥浆的本构模型符合宾汉模式,可以用方程τ=τ0+来表示,且裂隙层流扩散注浆压力符合式(18)的扩散规律。在实际裂隙扩散过程中注浆浆液始终处于流动状态,单次注浆时间基本都在数小时及以上。故设计试验探究流动状态下黏土水泥浆本构模型参数随时间的变化情况,以建立黏土水泥浆时变扩散方程。

3.1 试验步骤

研究选取上文4种代表性配比黏土水泥浆,按浆液配置标准流程在实验室配置好后,利用JJ-5型砂浆搅拌机并设置在低速模式,对浆液进行连续搅拌以模拟浆液的连续流动状态,并每1 h从搅拌缸取样一次利用旋转粘度计进行流变试验。

3.2 试验结果分析

3.2.1 本构模型方程的时变特性

如图4、表5所示,通过对流动状态下黏土水泥浆的本构模型随时间的变化情况进行试验研究可知,不同密度、不同粘稠度的4种配比黏土水泥浆浆液的本构方程随流动时间增加均呈现屈服应力和塑性黏度的增大的特性,且各配比浆液的流变模型均可以保持宾汉流型且不随流动时间而改变。

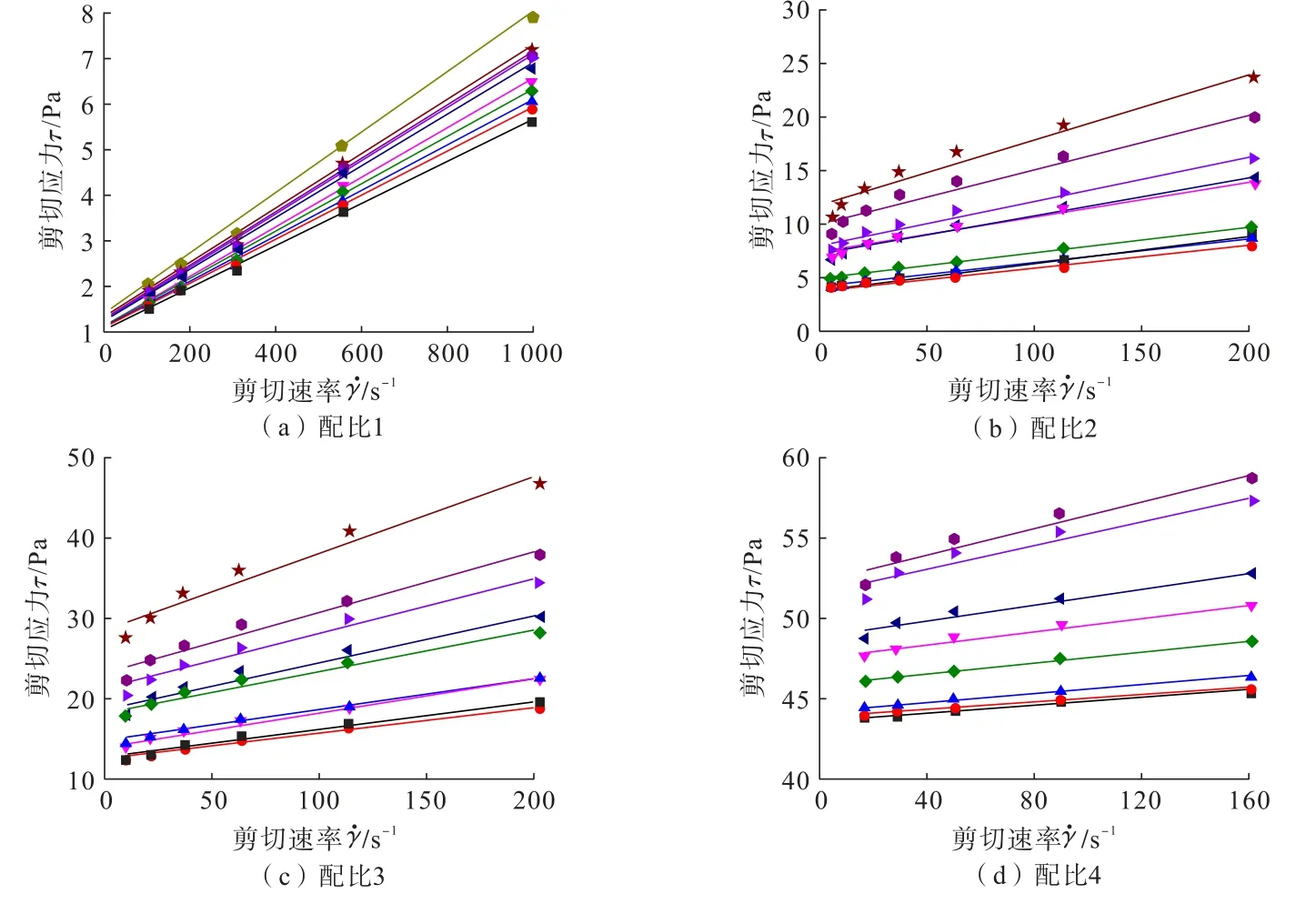
图4 配比1～4浆液不同时刻流变拟合曲线对比Fig.4 Comparison of rheological fitting curves of ratio 1～4 slurry at different times

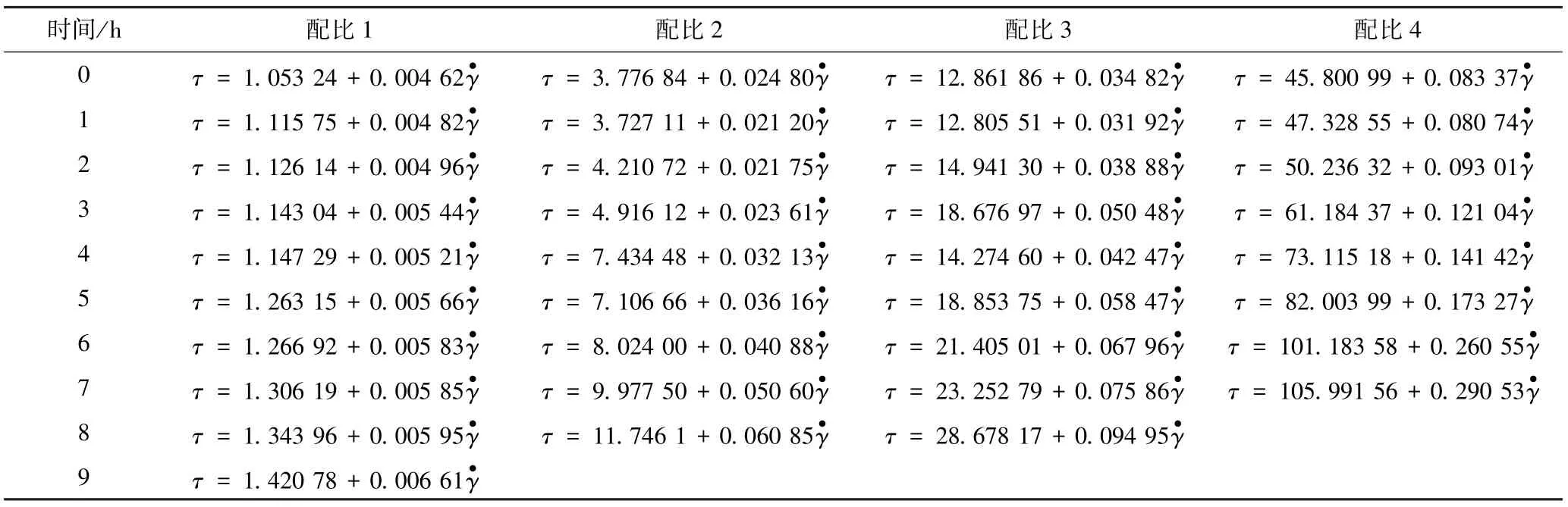
表5 配比1～4不同时刻拟合本构方程Table 5 Ratio of 1～4 different time fitting constitutive equation

3.2.2 本构模型参数的时变特性分析

3.2.2.1 屈服应力的时变特性

屈服应力τ0表示流变曲线的截距,也是浆液在流动过程中需克服的最小剪切应力,浆液剪切应力在到达该值前不会产生流动。通过前文浆液本构时变试验的拟合结果,便可以得到在连续流动状态下,浆液屈服应力τ0的时变数据。

通过对4种配比浆液屈服剪切应力进行时变特性分析,发现屈服应力均随时间呈指数增长,如图5、表6所示,且随着浆液密度及粘稠度的增加,屈服应力逐渐增大。通过幂指数函数τ0=τ00eAt进行拟合处理,相关程度较高,各配比拟合参数Adj.R2值分别为0.956 0、0.960 8、0.870 9、0.973 6。因此,认为黏土水泥浆的浆液屈服应力符合幂指数模型,同时可以得到各配比浆液屈服应力的时变函数关系式。

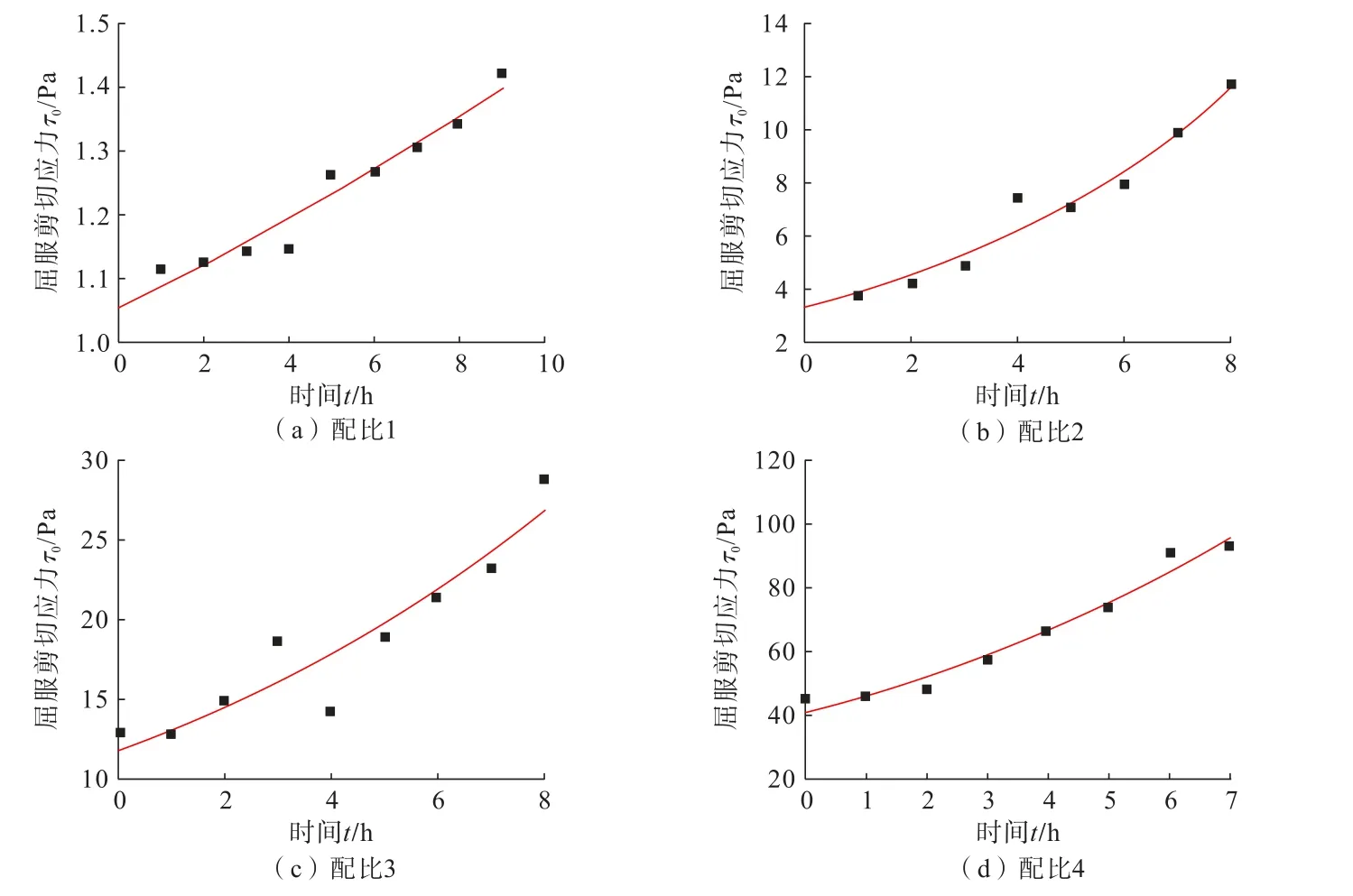
图5 配比1～4屈服应力时变方程拟合曲线Fig.5 Fitting curves of yield stress time-varying equation of ratio 1～4

表6 配比1～4屈服应力时变方程Table 6 Time-varying equation of yield stress for ratio 1～4

3.2.2.2 塑性黏度的时变特性

塑性黏度μ表示宾汉流体本构曲线的斜率,能够反映层流时泥浆中各相(固、液、气3相)间的内摩擦力大小情况,表征流体中的凝胶结构在受破坏后恢复保持原有状态的能力。宾汉流体浆液在某一时刻的塑性粘度值和牛顿流体类似,只和液体本身的性质有关,不随剪切速率的变化而变化,是表征宾汉流体流变特性的主要参数之一。

分析各配比浆液的塑性黏度随流动时间的变化情况,可以发现其随时间同样呈幂指数增长规律,且随着浆液不同配比间粘稠度的提高而增长愈加快速。利用幂函数μ=μ0eBt对塑性黏度时变规律进行拟合处理,拟合度较高,各配比拟合方程如图6、表7所示。

图6 配比1～4塑性黏度时变方程拟合图线Fig.6 Fitting curves of plastic viscosity time-varying equation of ratio 1～4

表7 配比1～4塑性黏度时变方程Table 7 Time-varying equation of plastic viscosity of ratio 1～4

3.3 建立黏土水泥浆的时变本构方程

通过以上内容的分析得到了黏土水泥浆的屈服应力及塑性黏度2个参数的时变函数关系式,在此基础上,便可以宾汉模型为基本模式建立黏土水泥浆时变本构方程。

黏土水泥浆的本构方程可以表示为τ=τ0+,又已知屈服应力随时间变化的函数关系式可表示为τ0=τ00eAt,塑性黏度随时间变化函数为μ=μ0eBt,式中参数A、B分别可以定义为黏土水泥浆浆液屈服应力以及塑性黏度的时变系数;τ00、μ0可以分别定义为初始屈服应力、初始塑性黏度。因此可以推导得到考虑时变因素的黏土水泥浆时变本构方程,表达式为τ=τ00eAt+μ0eBt。

根据试验结果,可以依次可以得到各配比浆液的时变本构方程,列于表8。