独立坐标系高斯投影实用算法程序实现及应用

姜韶,张坤先,匡志威

(1.四川省冶金地质勘查局测绘工程大队,四川 成都 610212; 2.长沙市规划勘测设计研究院,湖南 长沙 410007)

0 引 言

目前GNSS技术已经基本取代了传统大地测量技术,在城市测量、工程测量中已经成为主要的控制网测量技术。GNSS技术直接确定的是大地坐标系坐标(B、L、H),在实际应用中需要通过高斯投影正算计算出平面直角坐标系坐标。根据高斯投影边长改化公式,离中央子午线的距离、高程均会引起长度变形,因此在海拔较高的城市、地区以及线性工程的控制网测量中,均应考虑选择合适的中央子午线、相对参考椭球面来限制投影变形,精度要求应满足长度变形值不应大于 25 mm/km的要求。

随着无人机航空摄影测量技术的广泛应用,利用无人机机载RTK实时获取航摄相机曝光瞬间的高精度坐标信息,加上无人机IMU惯性测量单元的高度集成化、高性能化、组合化发展,现阶段无人机在小于1∶1 000比例尺的地形图测量中可以完全实现免像控。但是POS数据中的坐标一般都是地理坐标和椭球高,在海拔较高城市、地区以及线性工程为了限制变形,仍需要在空三前将坐标系统转换到独立坐标系和1985国家高程基准。少数的商业软件虽然具备独立坐标系投影计算功能,但是对数据格式有固定要求,往往需要单独将机载POS数据中的大地坐标数据提取,转换到独立坐标系后再替换到原POS数据中进行空三处理,数据格式的往返和人工编辑替换比较费事,不方便且容易出错。因此,经过程序开发实现高精度无人机机载POS数据的坐标批量自动转换可有效减少工作环节,有助于提高工作效率。

1 椭球膨胀法

椭球膨胀法是保持参考椭球的定位、定向和扁率不变,对椭球进行缩放,使得缩放后的参考椭球面与独立坐标系所选定的平面相切。因此,采用椭球膨胀法投影后得到的平面坐标在数值上与国家参考椭球的椭球面上的平面坐标接近,只是存在缩放关系,不会引起经度(东坐标)的变化,只要选择合适的投影面,就可以把高程所产生的变形降到最小,继而忽略不计。因此在建立独立坐标系时,通常采用椭球膨胀法。

1.1 算法流程

椭球膨胀法关键是计算膨胀后的新椭球的长半轴改正值dα,以及纬度改正值dB,具体的算法流程如图1所示。

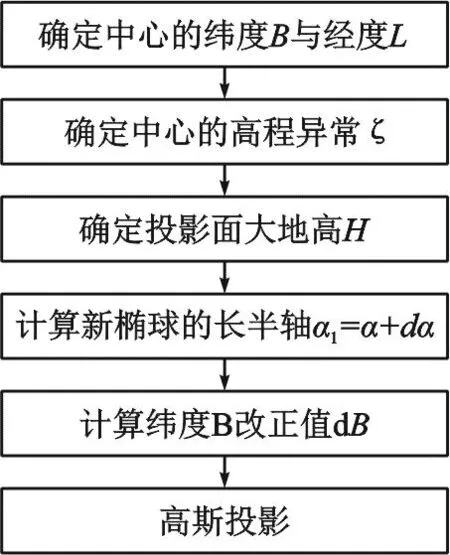
图1 椭球膨胀法算法流程

1.2新椭球的长半轴变化量计算公式

要满足椭球膨胀法的缩放条件,要求项目区的平均曲率半径R变化dR=H,其中H为区域的大地高。根据平均曲率半径计算公式:

(1)

(2)

(3)

将式(2)、式(3)代入(1)求微分得到:

(4)

式中:M为子午圈曲率半径,N为卯酉圈曲率半径,B为大地纬度,e为椭球的第一偏心率,α为原椭球长半轴,dα为缩放后椭球相对于原椭球的长半轴改正数,H为大地高。

1.3大地坐标改正公式

从国家参考椭球到缩放后的参考椭球的坐标由莫洛金斯基公式可得:

L=L0

(5)

(6)

上式中,L、B为缩放后的参考椭球对应的大地坐标,L0、B0为原国家参考椭球对应的大地坐标,H为大地高。

2 高斯投影通用算法

高斯投影正反算算法在很多文献中均给出了详细公式,在本文中将采用适用于不同椭球的高斯平面坐标正算的实用公式[3],本算法可以在编程语言或者Excel表格中简单实现。

(7)

(8)

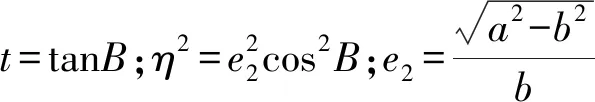
X=c0B-cosB(c1sinB+c2sin3B+c3sin5B)

(9)

式中,c0=Aa(1-e2)/ρ;c1=(C-B-D)a(1-e2)

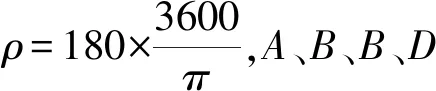
(10)

3 算法编程实现及精度验证

3.1 椭球膨胀法任意投影面高斯投影算法实现

基于本算法,在C#语言环境中开发小程序“基于椭球膨胀法任意投影面高斯正反算工具”,小程序界面如图2所示。选取四川西部某山区城市为例,投影面大地高为 2 600 m,投影中央子午线为102°,城市中心纬度为31°54′,现有GNSS控制点6个(CGCS2000坐标系),利用该程序转换到独立坐标系。

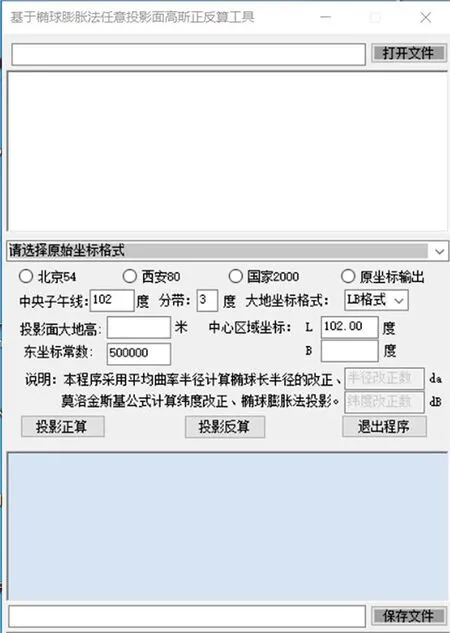
图2 基于椭球膨胀法任意投影面高斯正反算软件界面

3.2 POS数据坐标自动转换功能实现

为方便将无人机POS数据中的坐标转换到工程独立坐标系和1985国家高程基准,并按照规范要求进行航片编号等,本文利用C#语言实现POS数据坐标转换和航摄文件整理功能,程序界面如图3所示。其中平面投影转换采用上文算法,由于无人机航飞区域一般跨度较小,一般仅仅几平方公里,因此高程采用GNSS高程平面拟合即可。POS数据高程转换目标值(正常高)h由下式计算得到:

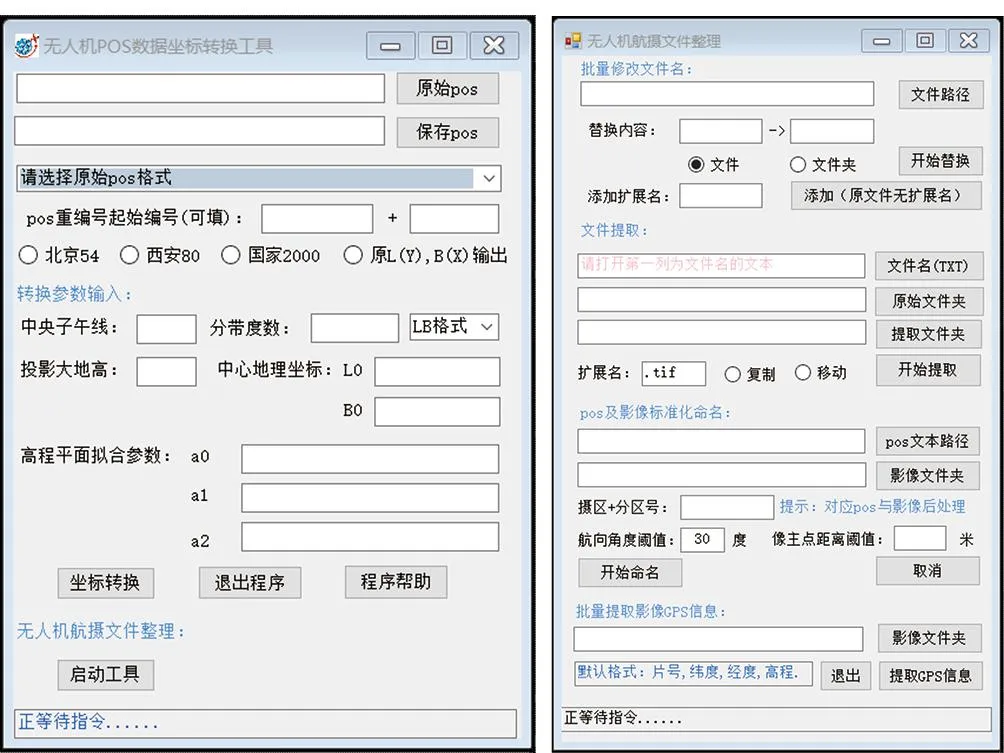
图3 无人机POS数据坐标转换及航摄文件整理工具界面

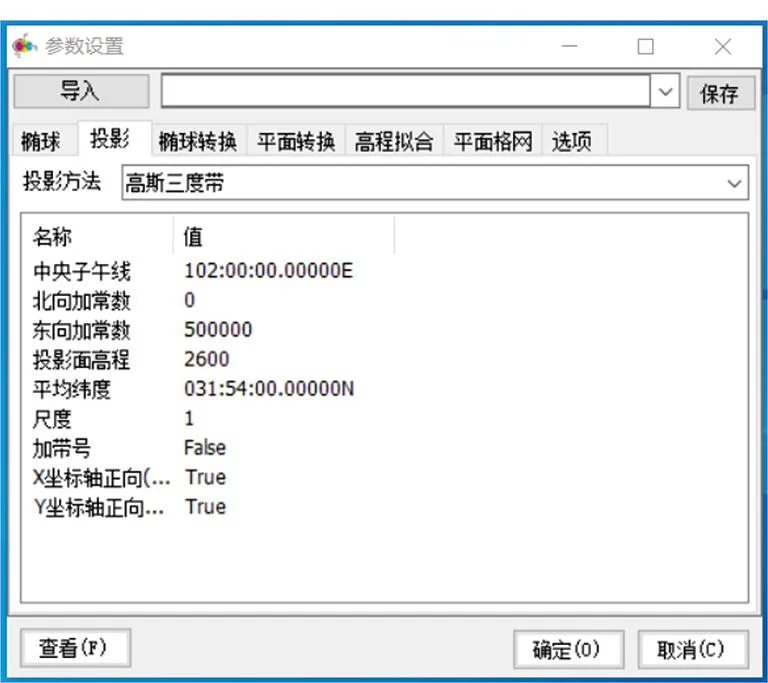
图4 HGO内置CoordTool软件界面

h=H-ζ

(11)

其中:

ζ=a0+a1×(B-B0)+a2×(L-L0)

(12)

式中:B、L为待转POS坐标点地理坐标;H为待转POS坐标点椭球高;B0、L0为测区中心地理坐标;a0、a1、a2为转换系数,由地面控制点计算得到。

3.3 椭球膨胀法任意投影面高斯投影算法精度验证

(1)HGO、CosaGPS软件投影计算

为验证本文实用算法投影后的长度精度,采用相同的参数用CoordTool软件(HGO软件内置系统工具)对以上六点进行坐标转换。打开CoordTool,“参数设置”界面上选择“源椭球”“当地椭球”均为“国家2000”;“投影”设置界面输入中央子午线为“102:00:00.00000E”,“投影面高程”为“2600”,“平均纬度”为“031:54:00.00000N”,其他默认;“选项”界面“椭球变形方法”勾选“膨胀”;返回程序主界面,打开源坐标数据进行高斯投影。

本文算法与HGO软件计算结果如表1所示。

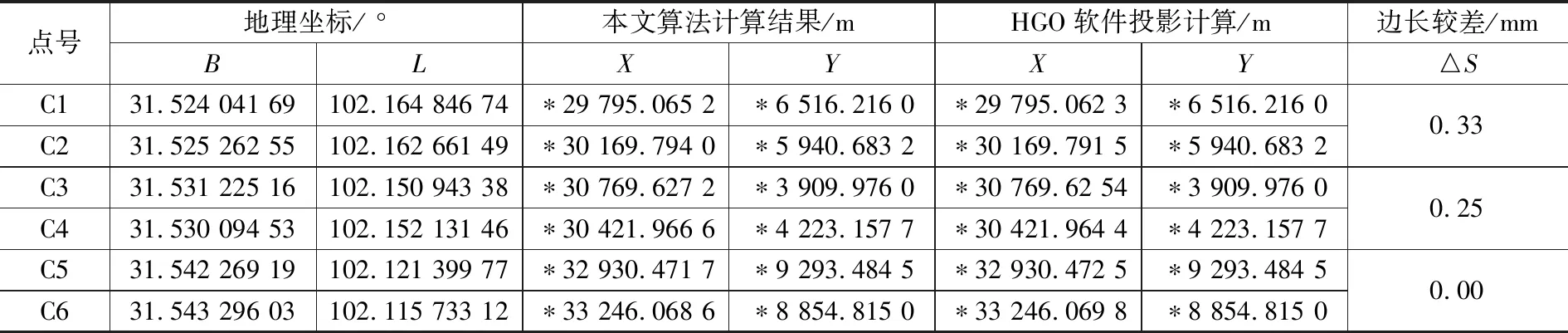
表1 本文算法与HGO软件计算结果比较

采用相同的参数用在CosaGPS软件里面设置好坐标系统、中央子午线、测区平均纬度、投影面大地高等参数进行坐标转换,具体设置如图5所示。

图5 CosaGPS软件坐标转换设置界面

本文算法与CosaGPS软件计算结果如表2所示。

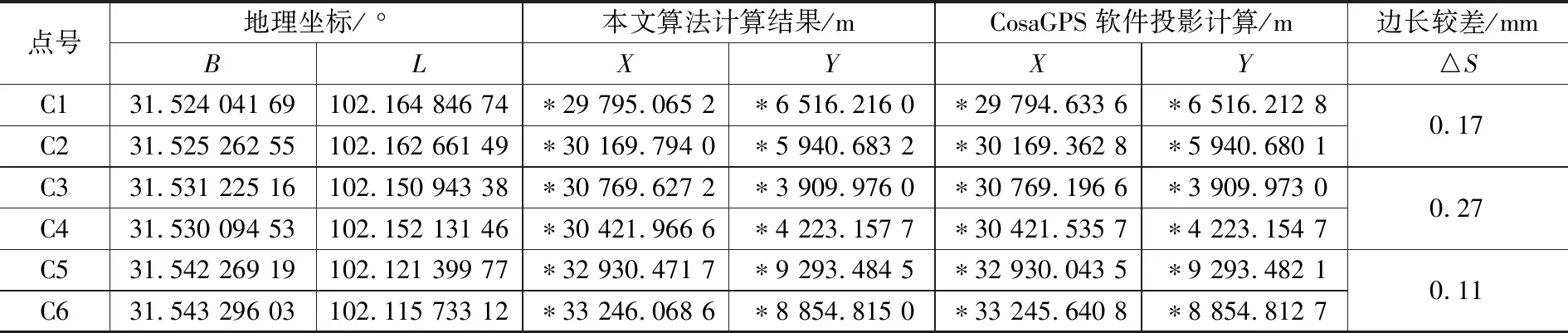
表2 本文算法与CosaGPS软件计算结果比较

由于与HGO、CosaGPS软件在计算新椭球的长半轴变化量及大地坐标改正值采用的公式、参数精度存在差异,因而计算结果存在细微差别,这种差值在随着投影面的高程增大而变大,投影点的纬度与中心纬度差值增大则变大。根据表1、表2可知,这种差值对边长影响较小,一般可以忽略不计。

(2)全站仪测距

为验证本算法的精度,采用全站仪对C1-C2、C3-C4、C5-C6边长进行观测,经过大气改正的边长观测值与本文计算结果反算的边长值对照如表3所示,可见均明显优于《工程测量标准》《城市测量规范》中对四等控制网最弱边相对中误差的要求。

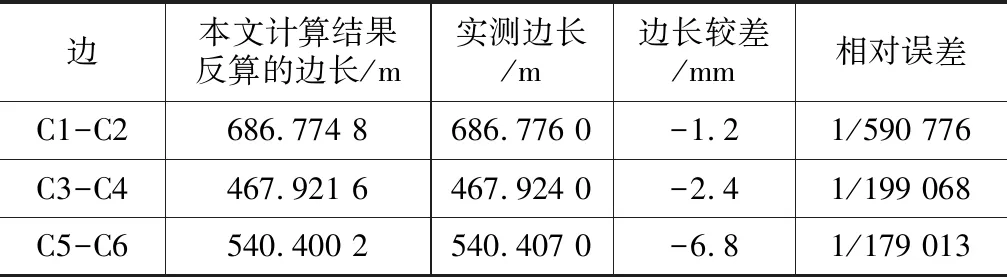
表3 边长精度验算成果

4 结 论

(1)本文采用的独立坐标系高斯投影算法简单实用,适用于各种椭球,不仅可以通过计算机编程语言实现,也可以利用Excel表格进行投影计算,投影精度可以满足一般城市地区、工程项目控制网测量要求。

(2)在进行独立坐标系高斯投影时,应选择合适的投影中央子午线、投影高程面、中心纬度。对于线性工程,比如高差较大的线路工程测量,应进行分带分区投影,确保投影后的边长变形满足工程精度要求。

(3)高精度无人机机载RTK技术在线路工程测量中已得到广泛应用,特别是带状地形图测量基本由无人机航测技术替代,将POS数据中的高精度坐标统一到工程独立坐标系中,有利于后期的空三加密处理工作,提高工作效率。

(4)本文算法有一定的局限性,单次投影的范围不宜过大,特别是高差较大区域应分区进行投影计算,注意控制计算范围。