型钢活性粉末混凝土柱耐火极限数值分析

周杨, 郑晓华

(山东建筑大学 土木工程学院,济南 250101)

0 引 言

型钢活性粉末混凝土(steel-reinforced reactive powder concrete, SRRPC)结构是一种新型组合结构,其既具有活性粉末混凝土强度高和体积稳定的特点,又具有型钢混凝土的延性和韧性。SRRPC柱一般是建筑体系中最重要的承重构件,其稳定性和承载力至关重要,结构柱的破坏会引起整体结构的破坏甚至倒塌,造成财产的大量损失甚至人员伤亡。在火灾作用下,建筑构件的材料性能和内部应力状况会发生变化,承载能力大幅降低,因此有必要研究高温条件下SRRPC柱耐火极限,为该结构的耐火设计提供参考。

许多学者对钢-混凝土结构在高温下的力学性能进行研究。刘书雷等[1]、陆洲导等[2]和廖杰洪等[3]开发纤维模型算法程序,研究三面受火钢筋混凝土连续梁的弯矩、位移以及承载力变化规律,发现三面受火构件的刚度和承载力都大幅降低,且其有限元模型可以较好地预测降幅。王广勇等[4]在试验的基础上建立火灾全过程作用下型钢混凝土柱的温度场和力学计算模型,以含钢率、受火时间、载荷比等参数为变量,利用单向热-力耦合分析研究高温作用后型钢混凝土柱的力学性能。

近年来,部分学者也对SRRPC结构在常温和火灾条件下的力学性能开展试验和有限元研究。王琨等[5]、WANG等[6]和王琨等[7]总结SRRPC柱的抗震性能。卜良桃等[8-10]重点研究在轴心及偏心载荷下SRRPC柱力学性能的变化,结果表明提高混凝土强度等级可以延缓裂缝的发展速度,且其极限承载力随含钢率的增大而增强。姜良芹等[11]和周绍朋等[12]建立SRRPC组合柱有限元模型并进行轴压和偏压分析,模型与试验结果吻合较好,可为实际承载性能提供参考。杨勇等[13]对火灾下配备活性粉末混凝土外壳的型钢混凝土柱的偏压性能进行有限元分析,发现混凝土柱的温度变化幅度由表及里逐渐降低,且其火灾后偏心受压破坏状态与常温下类似。

目前,对于火灾条件下SRRPC结构性能的研究仍相对缺乏。火灾下的结构试验具有危险性高、成本高、难度系数大等缺点,采用有限元模拟可以避免上述问题,达到预期效果。本文采用有限元分析软件Abaqus对不同截面尺寸、偏心距、配箍率、轴压比的SRRPC柱进行数值模拟分析,探究其温度场分布、轴向位移和耐火极限等方面的变化规律。

1 热-力耦合分析模型的建立

1.1 构件概况和模拟工况

建立边长为200 mm的正方形截面SRRPC柱模型,构件总长度为900 mm,中间600 mm为受火区,两端各150 mm为设置的延长段;在顶端施加载荷部位放置加载块,防止应力集中造成破坏而影响分析结果。内部型钢采用HW100×100×6×8的Q235热轧H型钢。箍筋采用直径为6 mm的HRB400钢筋,受火区箍筋间距为100 mm,延长段箍筋间距为40 mm。纵筋采用直径为12 mm的HRB400钢筋,长度为850 mm。构件的配筋和构造见图1。模型约束条件为:构件两端采用铰接方式,约束分别为U1=U2=U3=0与U1=U2=0。有限元网格采用DC3D20二次实体单元。

(a)配筋

1.2 热工参数

模型热工参数包括热传导系数、比热容、质量密度、热扩散系数、线膨胀系数等,钢材的热工参数及其表达式见表1,活性粉末混凝土的热工参数详细情况见表2。

表 1 钢材热工参数及其表达式

表 2 活性粉末混凝土热工参数及其表达式

1.3 力学参数

模型的力学参数包括:活性粉末混凝土塑性损伤本构模型和弹性模量,高温下钢材的塑性本构模型和弹性模量等。活性粉末混凝土本构关系及力学指标见表3,钢材本构关系及力学指标见表4和5。

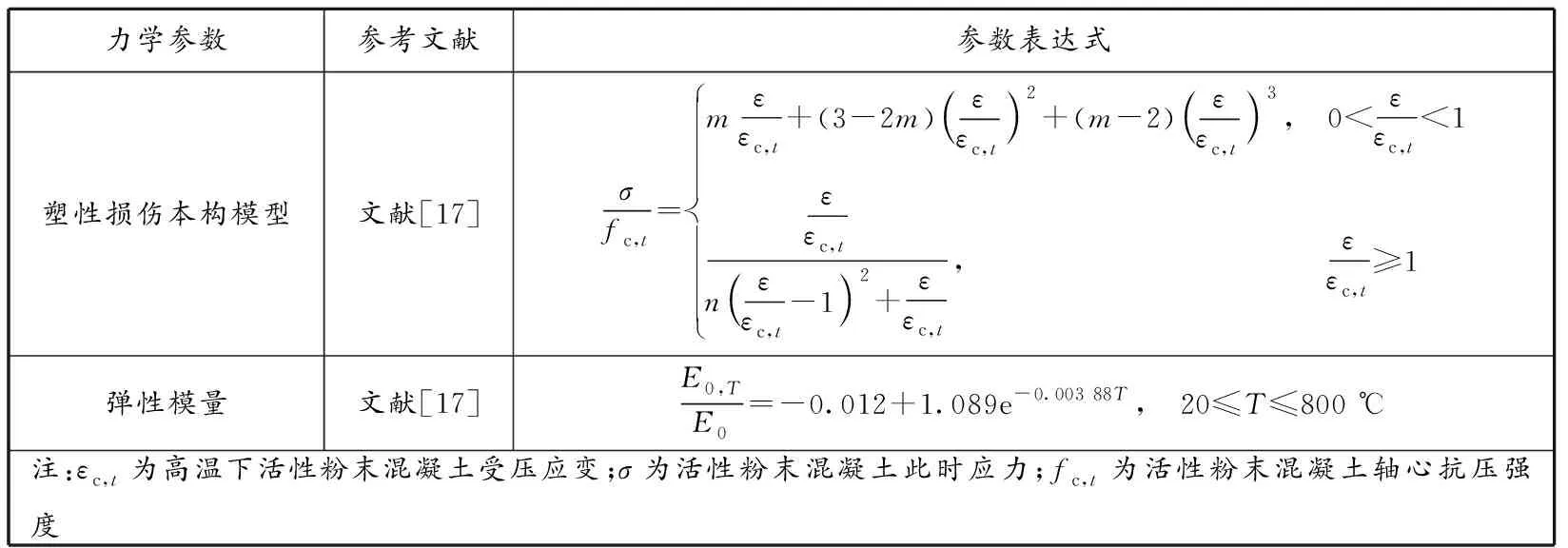
表 3 活性粉末混凝土力学参数表达式

表 4 钢材力学参数表达式

表 5 钢材弹性模量折减系数(文献[18])

1.4 分析过程

在恒载升温条件下,采用静力通用分析步,并基于此分析步设置轴向力。施加轴向力时,先将加载点与加载块顶面耦合,保持加载的一致性,然后以轴压比为0.6将载荷施加到耦合点上。

升温曲线采用实验室炉温曲线,即以4 ℃/min的速度升温。创建热传递分析步,用于设置温度场。在柱表面设置热交换条件,并将升温曲线导入环境温度。除此之外,柱表面还有大量热力辐射,综合辐射率取0.7。因为在加热过程之前构件位于室内,所以场初始温度设定为20 ℃。温度场分析定义绝对零度为-273 ℃,Stefan-Boltzmann常数设定为5.67×10-8。

2 模拟结果与分析

2.1 温度分析

构件的温度场分布结果见图2。在高温下达到耐火极限时,整个模型柱上下被均匀加热,故取中间高度截面剖开,观察构件内部温度场分布。在截面上选取7个代表性测点见图2(b),其最低温为327 ℃(测点3),最高温为576 ℃(测点6)。从柱核心到最外层温度均匀上升,越靠近边缘温度越高,且钢筋温度比周围混凝土温度高,原因是钢筋的导热性能优于混凝土,温度升高速率比混凝土快。

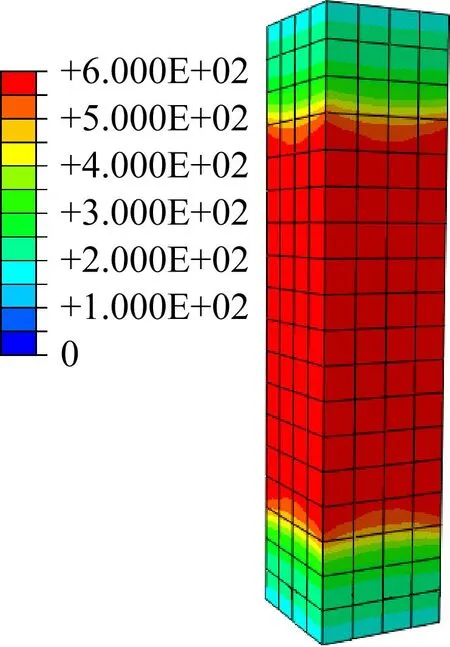
(a)整体

2.2 轴向位移及破坏模式

构件的宏观位移和轴向位移曲线见图3。构件纵向压缩、横向膨胀,为压缩破坏。构件位移先缓慢上升、后快速上升。在温度上升初期,构件轴向位移没有明显变化,此时构件温度较低,在温度场下产生的膨胀能抵消构件受载荷引发的部分压缩,构件位移随温度升高保持平缓增长。随着温度的进一步升高,构件力学性能退化,承载力下降,产生的膨胀无法抵消构件的压缩,且这种情况随时间的增长和温度的升高愈加明显。

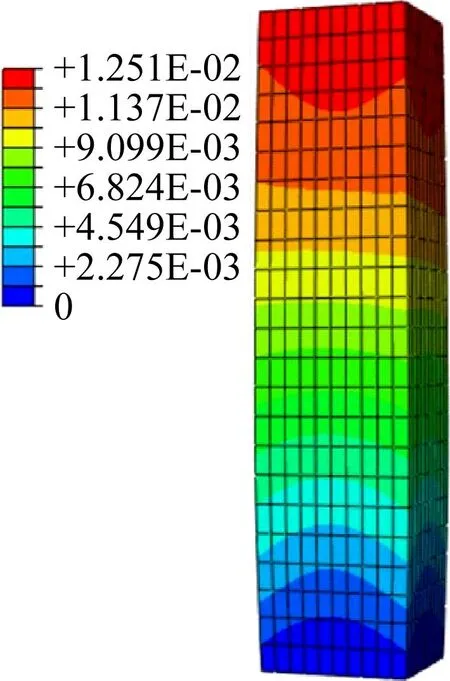
(a)宏观位移

2.3 试验对比

为验证模型的可靠性,取文献[19]的试验进行对比分析。该试验研究高温下箍筋间距对耐火极限的影响。先对试件加载至预定载荷,然后按照预定升温曲线进行升温加载,直至试件轴向位移达到6 mm时试验结束。本文模型所用的尺寸、材料、升温制度、约束条件均与文献[19]一致。

选取部分温度测点,对比试验温度与模拟温度,结果见图4。模拟升温曲线与实际升温曲线吻合度较高,走势基本相同,到达耐火极限的温度相差不大。在升温的过程中,试验温度略高于模拟温度,这是由于在试验中,试件在载荷和高温耦合作用下产生大量裂缝,因此热电偶的温度升高速率较快,而模拟温度场中未考虑裂缝的开展情况,所以温度略低于试验温度。

图 4 试验和模拟温度曲线对比

模拟和文献[19]试验的轴向位移曲线对比见图5。模型构件的位移走势与试验结果基本相同,先经历平稳上升阶段,然后进入高速上升阶段。当构件到达耐火极限的破坏标准(即构件位移到达6 mm)时,模拟构件耗时316 min,试验耗时334 min,总体相差仅5.6%,小于6%,模拟结果较为准确。有限元分析是相对理想化的过程,考虑混凝土各向同性、属于均质材料,得到的位移曲线曲率相对较大,转折相对柔和,没有试验曲线上的尖锐拐点。总体来说,此模拟可用于SRRPC柱结构的分析研究。

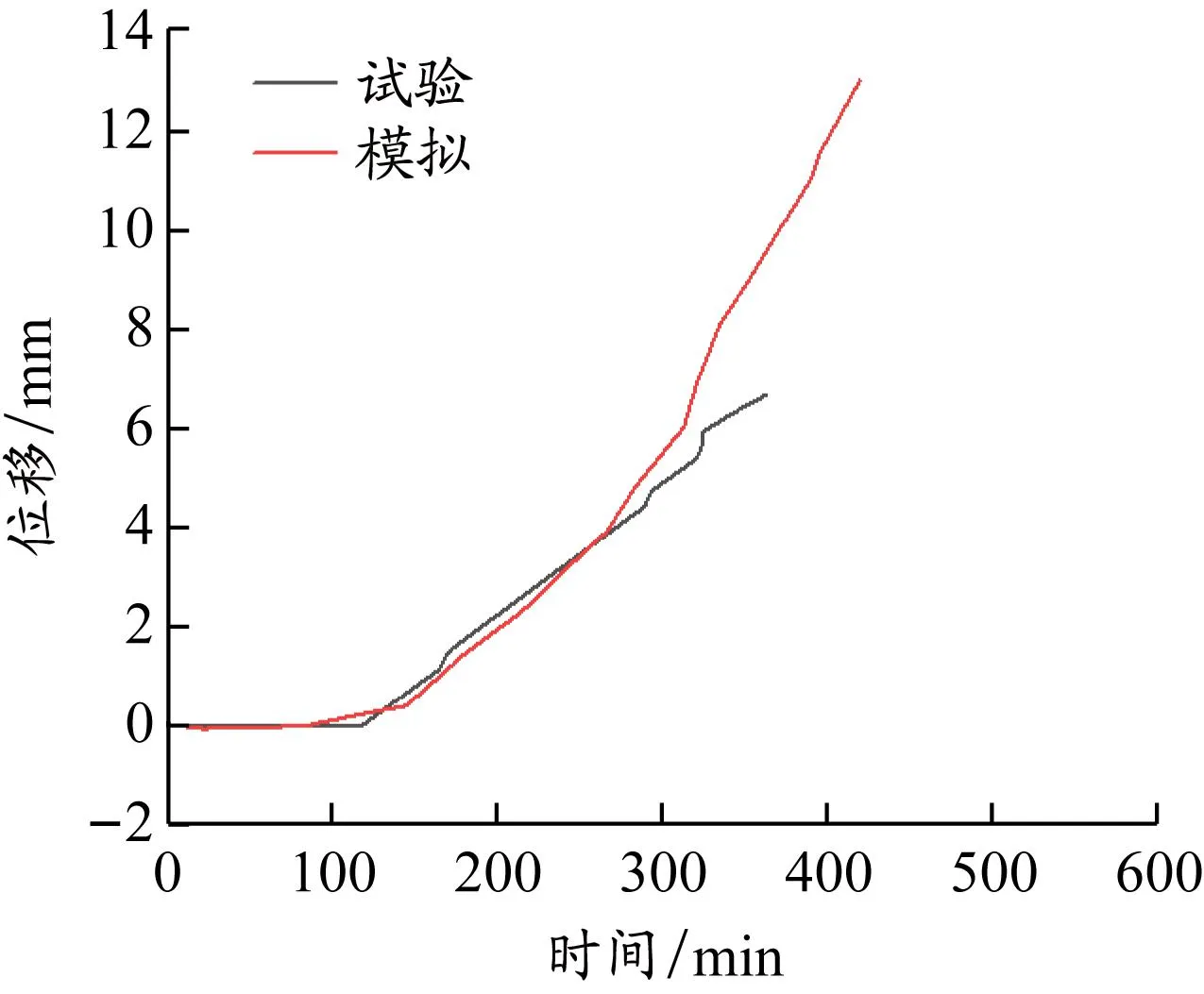
图 5 模拟和试验轴向位移对比

3 影响因素分析

研究四面受火的SRRPC方形柱,其中对照组构件截面为正方形,宽度b和高度h均为200 mm,偏心距e=0,配箍率0.28%,计算高度取600 mm,采用C120级活性粉末混凝土和HRB400级热轧钢筋,型钢采用HW100×100×6×8的Q235级钢。在室温20 ℃时,活性粉末混凝土构件的轴心抗压强度为95.45 MPa,钢筋屈服强度为468 MPa,钢筋极限强度为613 MPa,型钢屈服强度为251 MPa,型钢极限强度为386 MPa,混凝土钢纤维添加率为2%。

SRRPC方形柱耐火极限的影响参数有截面尺寸、偏心距和配箍率。构件的截面参数见图6。截面尺寸的变化可以理解为长细比λ的变化,

λ=μL/i

(1)

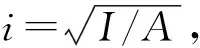
主要影响参数设置如下:

(1)构件截面边长分别设为180、200、220、240和260 mm;

(2)单双向偏心和偏心距设置为:偏心加载点分别沿α=45°和纵轴(α=0°)方向分布,偏心距为e分别为25和50 mm;

(3)配箍率分别为0.28%、0.38%、0.47%、0.57%和0.71%,即箍筋间距分别为100、75、60、50和40 mm;

(4)轴压比分别为0.2、0.3、0.4、0.5和0.6。

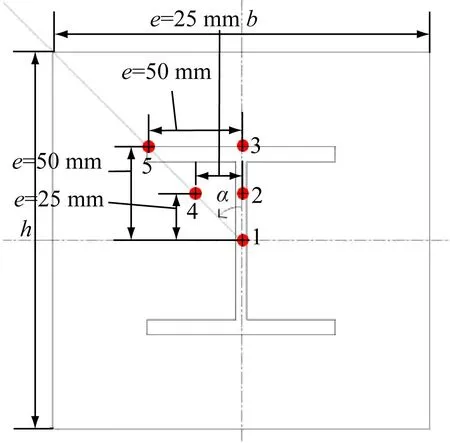
图 6 模型柱截面参数示意

3.1 截面尺寸对耐火性能的影响

模型编号Z-1到Z-5依次为截面边长180、200、220、240和260 mm构件,温度场分布结果见图7,测点温度和耐火极限结果见表6。

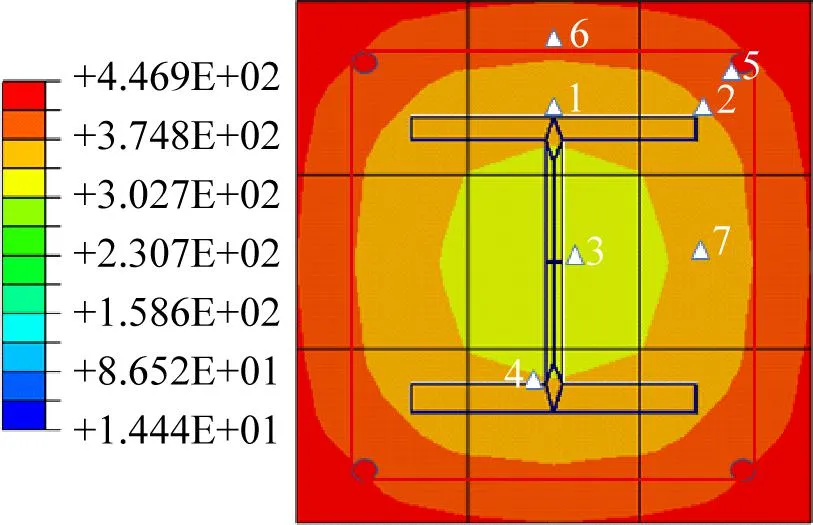
(a)Z-1

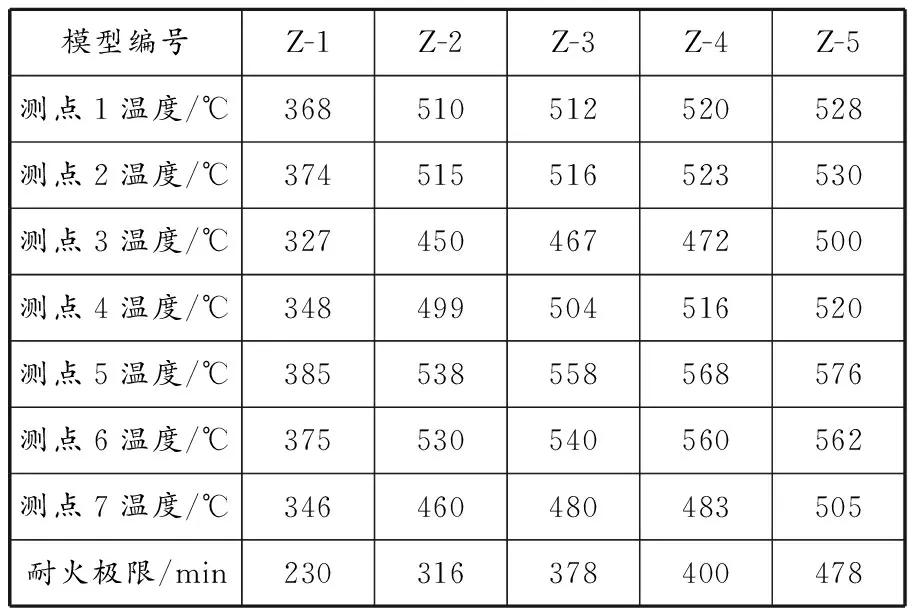
表 6 不同截面尺寸构件测点温度和耐火极限

测点1～7温度均随截面尺寸增大而升高,且越靠近边缘的测点升温越快(如测点5和6),最终温度最高的是测点5,略高于测点6。测点5受2个面温度传输的影响,并且测点5同时受到纵向钢筋和箍筋传递的热量,得到的热量最多。以温度最高的测点5为例,其温度从374.8 ℃升高到576.0 ℃,构件模型温度经历较大跃迁,增长53.7%,温度增长速率呈逐渐减缓的趋势。从宏观来看,截面尺寸越大,构件到达耐火极限时间越长,燃烧越透彻,各测点温度越高,且各测点之间温度相差越小(即等温线越密集)。

不同截面尺寸构件的轴向位移曲线见图8。位移曲线走势大致相同:构件受热膨胀,导致位移曲线初始经历大约100 min的平缓增长段,之后构件在火中的承载能力逐渐衰退,位移曲线步入稳定增长段。随着构件截面尺寸的增大,位移增长速率略有放缓,到达耐火极限点(以模型位移达到6 mm时为破坏标准)的时间也越长(230～478 min)、跨度较大,说明截面尺寸对构件在火中的位移具有一定的影响。构件呈延性破坏,符合轴压破坏特征,且截面越大延性破坏特征越明显。

图 8 不同截面尺寸构件的轴向位移曲线

3.2 配箍率对耐火极限的影响

截面边长取200 mm,不同配箍率构件的模型参数见表7。温度场分布结果见图9,测点温度和耐火极限结果见表8。模型箍筋间距自100 mm缩短至40 mm,模型的最高温度为600～630 ℃。因为炉膛最高温度是630 ℃,所以构件温度相差较小。构件截面对称且加载与加热方式为关于截面对称,因此构件的温度场均呈均匀对称分布。构件温度从中心向外发散式升高,所以7个测点中温度最低者为测点3、最高者为测点5,温度最大相差95 ℃。构件G-1到G-5的模型总体温度逐级升高,随着温度升高,模型内部温度梯度逐渐变得紧凑,最终内外温差逐渐降低,各测点温度同炉温保持一致。

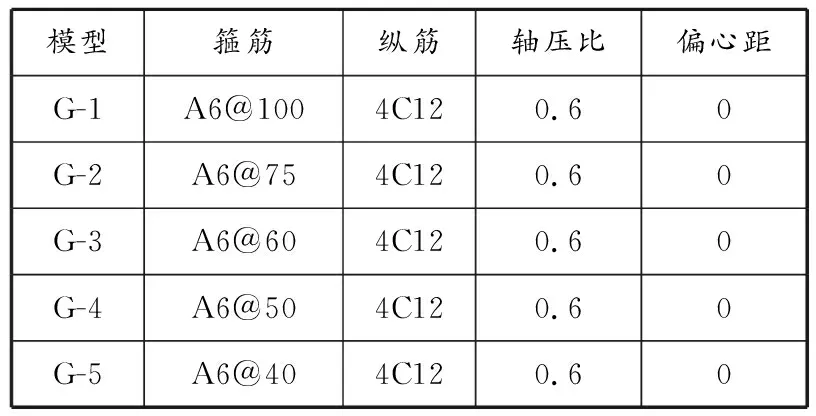
表 7 不同配箍率构件模型设计参数

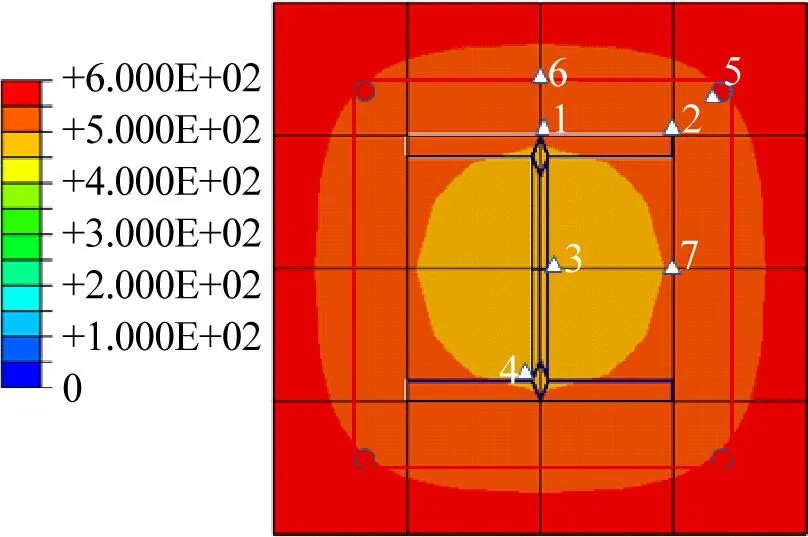
(a)G-1

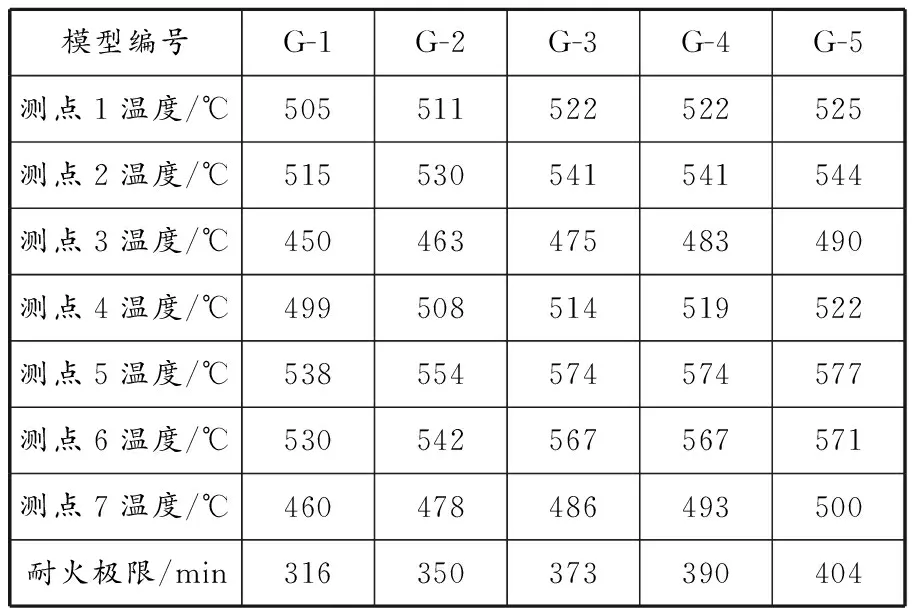
表 8 不同配箍率构件测点温度和耐火极限

不同配箍率构件的位移曲线见图10。5条曲线走势基本相同,均经历缓慢上升阶段和稳定上升阶段。在前150 min内,由于模型有微膨胀,方向与轴压方向相反,所以位移在初期缓慢增加甚至在较低轴压比的情况下出现负增长状况;而后期材料性能逐渐劣化,在稳定载荷下模型位移增长速率增加,形成稳定增长段。在加载初期,5条曲线紧密贴合在一起,到后期稳定上升段,各直线增长速率出现分歧,箍筋分布较为紧密的模型,其位移增长较箍筋分布稀疏者慢,曲线也更加平缓。紧密的箍筋能延缓混凝土出现裂缝破坏的时间,使构件的延性得到很好的改善。

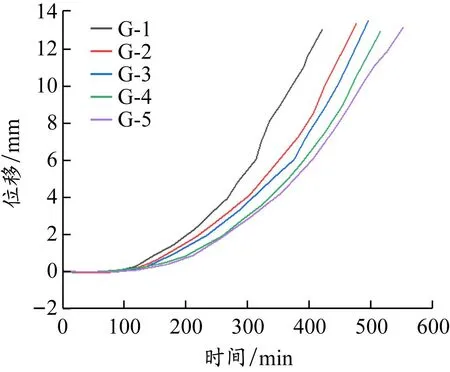
图 10 不同配箍率构件位移曲线

进一步分析,箍筋只能起到抗剪和约束混凝土的作用,对极限承载力贡献不大,所以5条曲线分布差异并不显著。与轴压比较小的情况相比,在轴压比较大的条件下,配箍率对于方柱耐火极限的影响更加明显,轴压比为0.6时,在耐火极限同比增加28%的情况下,增大配箍率可延长模型耐火极限。

3.3 偏心距/偏心角对耐火极限的影响

截面边长取200 mm,不同偏心距构件的模型参数见表9。温度场分布结果见图11,测点温度和耐火极限结果见表10。Y-1为轴心加载构件,承载力最高,达到耐火极限时的温度最高;Y-2、Y-3分别为单向偏心受压25和50 mm的构件,承载力次之,达到耐火极限时的温度有所下降;温度最低的是Y-4和Y-5双向偏心受压模型,承载力最差。相同加载角时,偏心距大的模型在高温下较容易破坏,其耐火极限小,达到的温度低。按照最终达到的温度(耐火极限)由低到高排列构件依次为Y-5、Y-3、Y-4、Y-2、Y-1,且温度下降出现断层。以测点3为例:轴心加载时最低温为450 ℃;当偏心距为25 mm时,单向偏心和双向偏心构件的温度已经分别降至350和325 ℃,降幅较大,分别为22.2%和27.7%;当偏心距增至50 mm时,单、双向偏心构件的温度分别降至254和217 ℃,幅度分别为43.5%和 51.7%,呈断层式下降。双向偏心模型温度下降幅度较单向偏心模型大,偏心距(尤其是双向偏心)对构件温度和耐火极限的影响非常大。

表 9 不同偏心距/偏心角构件模型设计参数

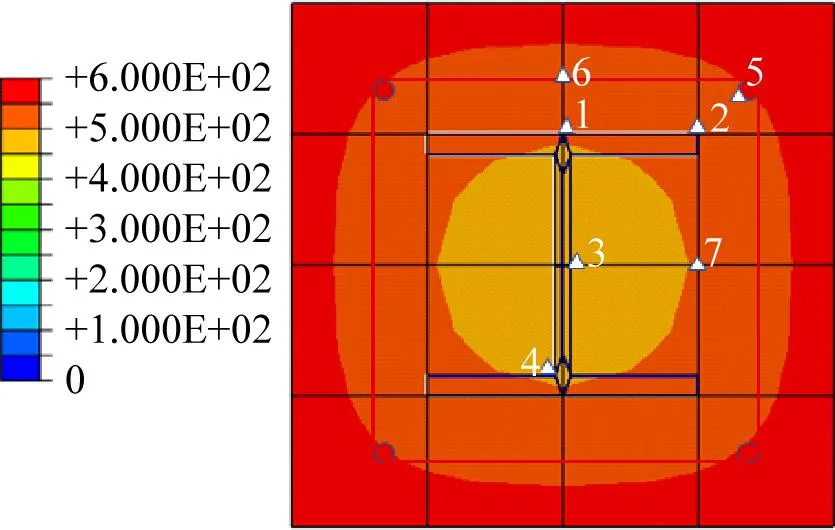
(a)Y-1

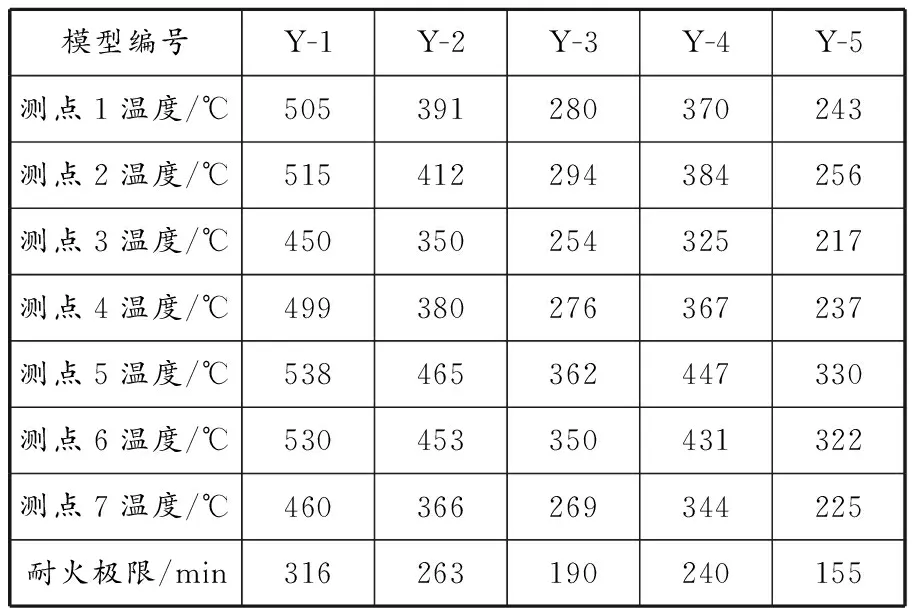
表 10 不同偏心距/偏心角构件测点温度和耐火极限

取构件模型顶面轴心点绘制其轴向位移变化曲线,见图12。图12(a)的5条位移曲线趋势大体类似,都是由于高温膨胀作用先经历缓慢上升段,后由于构件材料性能的退化进入稳定上升段。随着偏心距以及加载角的增大,构件的耐火极限越来越小。将影响因素进一步细分,分别比较加载角一定时偏心距的影响效果(图12(b))和偏心距一定时加载角的影响效果(图12(c))。在加载角一定的情况下,偏心距越大,模型压缩的延性越大,位移走势越平缓,耐火极限越低,且加载角大的模型降低更加明显、幅度更大;在偏心距一定的情况下,加载角越大位移走势越连续,越没有明显的拐点,构件延性越强,模型耐火极限越低,且在偏心距离较大时十分明显。偏心距/偏心角对耐火极限的影响较大,相较于轴心加载,偏心45°/50 mm模型的耐火极限同比下降50.9%。

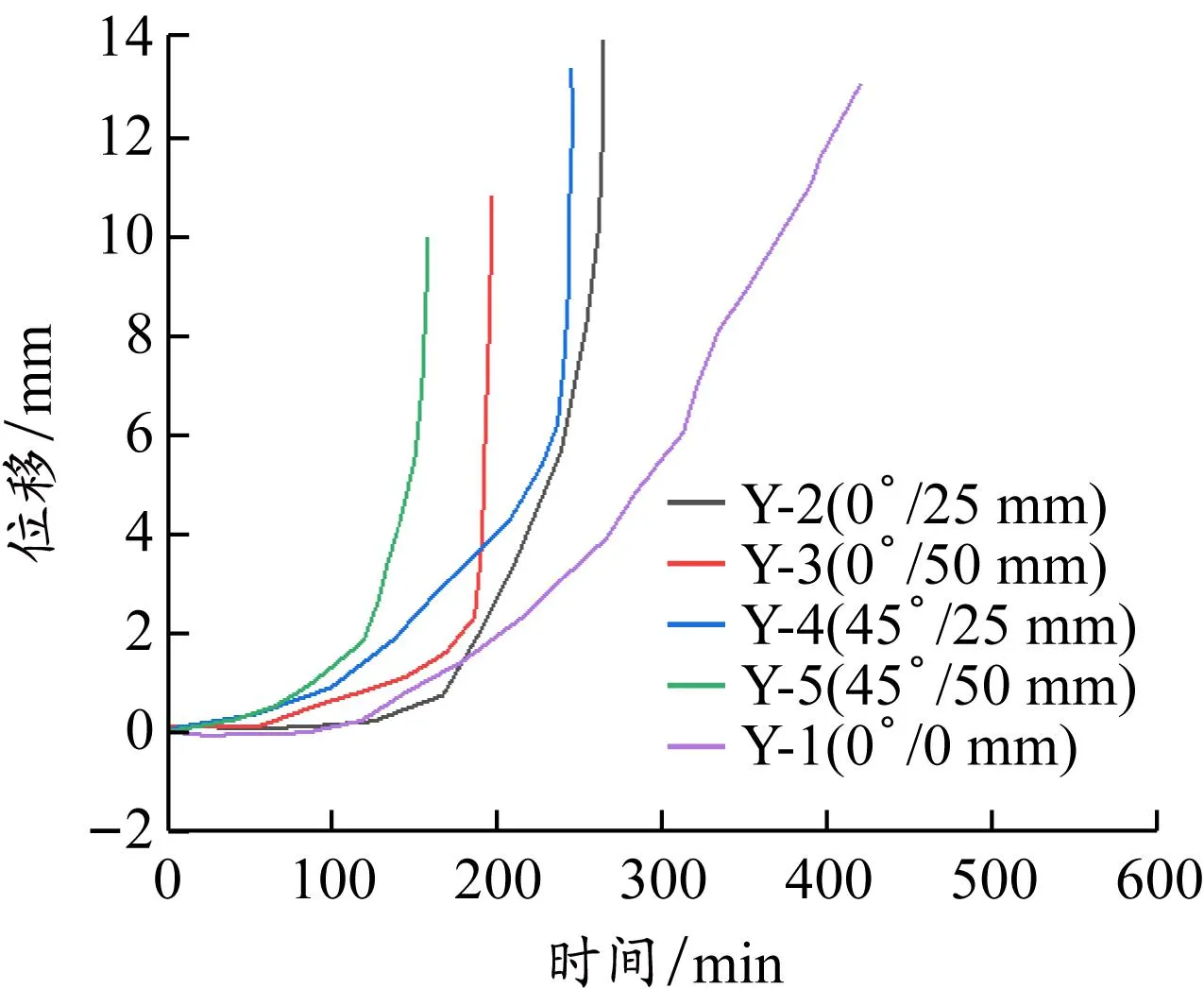
(a)总体轴向位移

3.4 轴压比

截面边长取200 mm,不同轴压比构件的模型参数见表11,测点温度和耐火极限结果见表12。随着轴压比升高,各测点温度有所下降。钢材对温度较敏感,始终比混凝土温度高。轴压比越低,构件在火中持续受载荷的时间越长,构件被燃烧得越透彻。提取构件模型的位移曲线,见图13。

表 11 不同轴压比构件模型参数

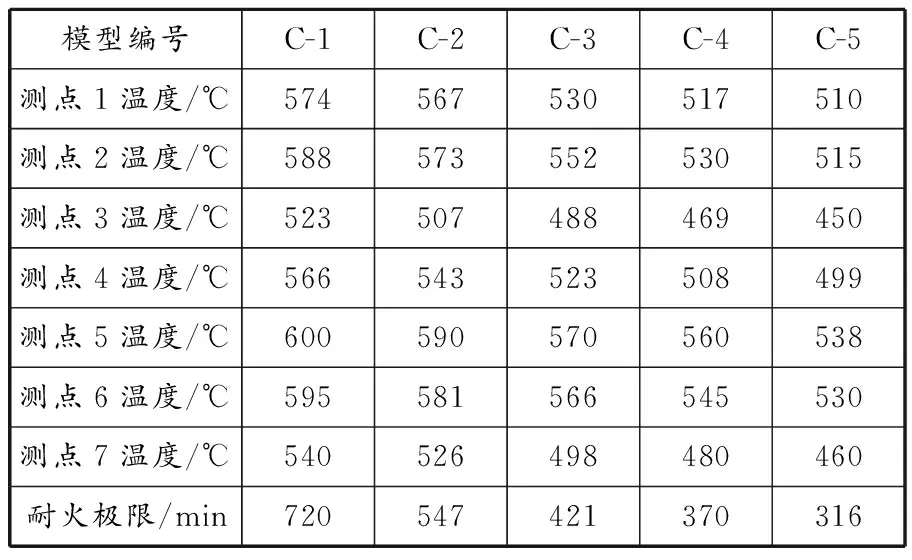
表 12 不同轴压比构件温度

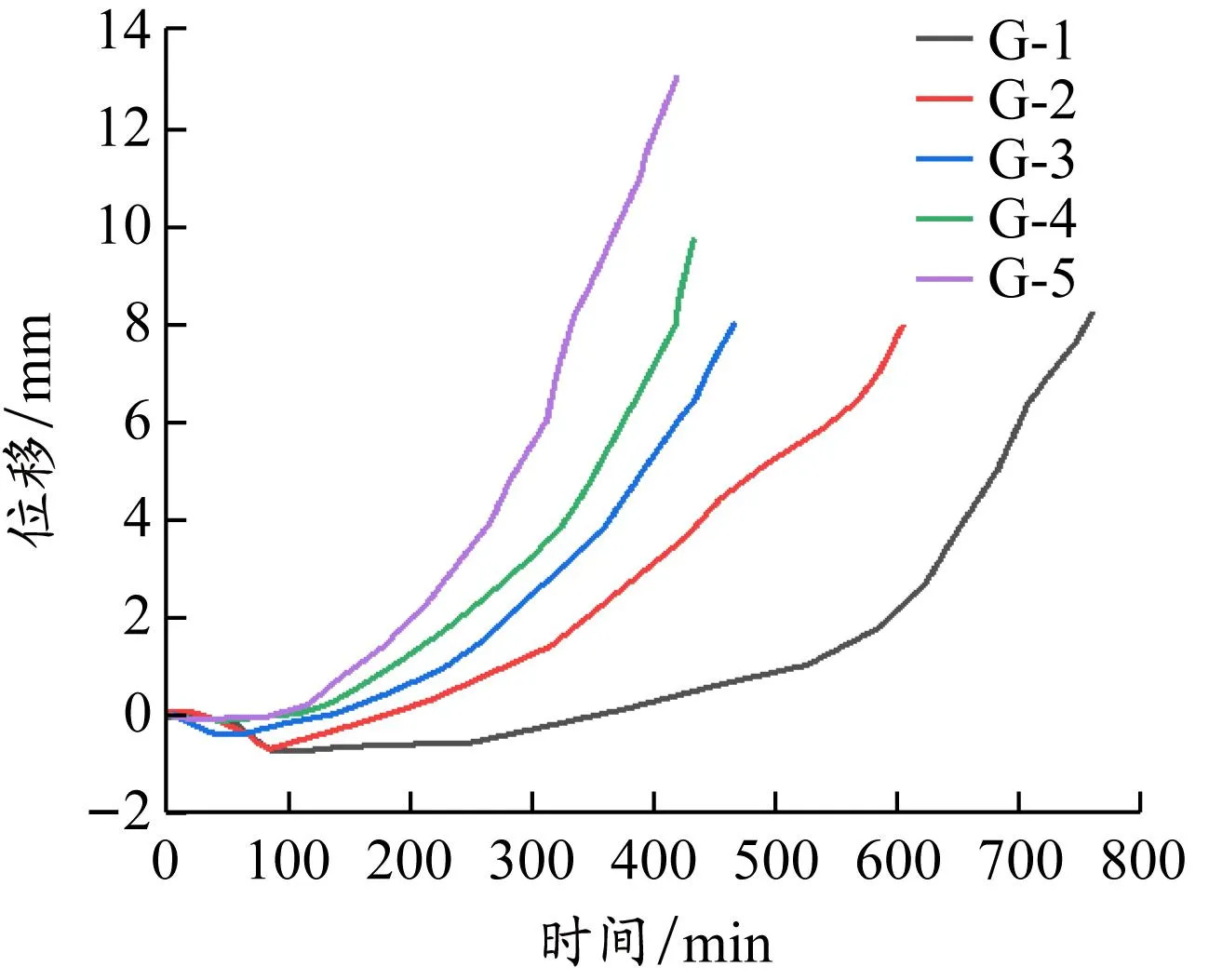
图 13 不同轴压比构件轴向位移曲线对比

轴压比较小的构件其位移增长较为缓慢,短柱被缓缓压坏,整体位移不大,与轴压比较大的构件差距较明显,特别是耐火极限,最大相差404 min。轴压比较小的构件其位移曲线有明显的膨胀段,即初始位移方向与轴压方向相反时。其原因是在热胀冷缩作用下,构件在受较小轴向载荷时产生的轴向压缩不足以抵消受热产生的膨胀,于是表现出反方向的位移。当构件受到的轴压比≥0.5时,这一段反方向位移就可以被轴向位移抵消;之后构件受高温的影响,弹性模量、刚度下降,性能退化,正向位移增长速率逐渐加快,因此由平缓的上升转为快速上升。

4 公式推导

基于以上参数分析,结合目前国内外钢筋-混凝土结构耐火极限研究资料,修正文献[20]中的公式,当0.2 m≤b≤0.6 m、b≤h≤0.6 m、0≤e≤0.05 m、0.22%≤ρ≤0.71%时,提出SRRPC的耐火极限公式:

当α=0°时,

T=412+(-75 268)/((Rf-195.4)2+325.8)

(1)

当α=45°时,

T=155+85 246.76/((Rf-287)2+1 003)

(2)

其中:Rf=βμβLβhdbβbβeβρ

(3)

当α=0°时,

βμ=1.696μ2-3.225μ+1.693

(4)

βL=-1.026L+6.634

(5)

βhdb=-0.326(h/b)2+3.251(h/b)-0.07

(6)

βb=0.003b+0.2

(7)

βe=0.932e3+4.07e2-6.727e+11.166

(8)

βρ=4 857ρ

(9)

当α=45°时,

βμ=1.327μ2-2.328μ+1.167

(10)

βL=-1.233L+10.119

(11)

βhdb=-1.046(h/b)2+4.242(h/b)+1.146

(12)

βb=1.614b-0.209

(13)

βe=-2.956e3+124.24e2-450.66e+31.138

(14)

βρ=4 656ρ

(15)

式中:μ为载荷;L为计算高度;h和b分别为构件截面的高和宽;e为截面的偏心距;ρ为配箍率。

对比耐火极限的有限元分析结果与公式计算结果,误差见图14。大部分数据都在合理误差范围内,说明该理论计算公式可用于SRRPC柱的耐火极限计算。在加载角α=0°和α=45°的基础上,可以通过插值法确定其他加载角加载状况下的耐火极限。

图 14 耐火极限结果误差

5 结 论

利用有限元分析软件Abaqus建立SRRPC柱的热-力耦合模型,并将模型计算结果与试验结果进行对比验证。在基本模型的基础上,进行截面尺寸、偏心距、配箍率、轴压比等影响因素的参数分析,得到以下结论:

(1)在恒载升温条件下,构件位移先缓慢上升、后快速上升:在温度上升初期,构件在高温下产生的膨胀可抵消载荷效应下的部分位移;随着温度的升高,构件的力学性能降低,轴向位移进入快速发展阶段。

(2)随着截面尺寸和配箍率的增大,构件耐火极限增加;随着偏心距和轴压比的增大,构件耐火极限降低;截面尺寸、偏心距和轴压比对耐火极限的影响明显大于配箍率。

(3)基于参数分析,修正已有文献中钢筋混凝土柱耐火极限公式,提出SRRPC的耐火极限公式,计算结果与数值分析结果吻合度较高。

通过Abaqus有限元软件对SRRPC柱进行模拟分析并达到预期效果,可为SRRPC结构的数值分析研究提供参考。