VAR模型中的异常值处理及应用

位雪丽

(河南财经政法大学经济学院,郑州 450046)

0 引 言

新冠疫情暴发导致各国经济增长均经历了断崖式下跌,随着经济逐渐恢复,各国经济指标又出现跳跃式上涨,最终导致疫情发生以来各种经济指标均出现大幅波动,加剧了时间序列数据的不平稳,给模型估计带来挑战。直接去掉极端观测值会导致数据不连续和低估经济波动,而直接将其当作正常值使用又可能会扭曲参数估计结果,因此研究经济变量之间关系时必须选择适当方法处理极端观测值。另外,使用贝叶斯方法估计VAR模型时主观设定模型参数的先验分布可能会影响参数的后验估计值。本文基于分层建模思想对模型参数先验分布中的参数设定分布范围,对极端观测值对应的方差进行建模,以区分不同程度的冲击,一定程度上降低了主观选择对先验分布的影响,使研究结论更有参考价值。

1 文献综述

新冠疫情发生以来,大量学者使用VAR模型研究疫情冲击下经济变量之间的关系[1],部分学者直接将疫情防控期间的样本观测值当作正常值对待。例如,刘达禹等通过构建TVP-VAR模型来研究疫情暴发背景下政策不确定性冲击对我国三次产业的非均衡影响[2]。李能丽和王林使用VAR模型研究了新冠疫情发生以来美国、欧元区、日本的不限量资产购买、零利率等极度宽松的货币政策对我国工业经济的影响[3]。也有部分学者在采样时直接舍弃疫情防控期间的数据。例如王振中等使用2002年1月至2019年12月的数据研究中国居民消费价格指数的动态结构[4]。肖强和汪卢俊使用2004年1月到2018年12月的数据构造中国的FCI指数[5]。梁永玉和田茂再使用2009—2018年的面板数据研究我国东、中、西部以及各省份经济高质量发展的时空特征[6]。为了提高研究结论的现实借鉴价值,需要将疫情防控期间的样本数据纳入研究范围,并对其进行特殊处理。

在模型参数的估计方面,鉴于贝叶斯估计可以同时利用参数的先验信息和变量的样本数据信息,在使用VAR模型进行实证研究过程中应用贝叶斯方法估计模型者较多。使用贝叶斯方法涉及模型参数的先验选择,参数的先验分布总体上有两类:第一类是无信息先验,比如均匀分布,对于一定区间内的参数可能值没有倾向性;第二类是信息先验,是一种带有先验信念的主观先验,常用的有Gamma分布、Wishart分布和Beta分布等。而先验分布中依然有相应参数需要设定,为了降低主观信念对参数估计值的影响,很多研究对先验分布中的参数进一步设定先验分布,即分层建模。这种分层建模方式可以减少先验设置中主观选择的参数数量,弱化对参数估计结果的影响,并且模型包含的变量越多,分层模型的预测性能越好。

新冠疫情发生以来经济指标大幅波动对VAR模型的估计构成了挑战。当进行模型统计推断时,这些极端观测值是否会扭曲模型的参数估计值?另外,由于疫情防控期间的数据将“污染”疫情之后的时间序列观测值,因此本研究对于未来使用完整观测数据做研究也很重要。本文基于分层建模思想对先验分布中的参数进一步设定先验分布,同时对疫情防控期间的冲击波动率进行单独设定,通过模拟疫情发生以来冲击波动率的变化来解释疫情带来的巨大宏观经济冲击。结合超参数估计、脉冲响应和密度预测可以看出,本文的处理方法更具合理性。

2 模型构建

本文主要论述在估计VAR模型时如何处理极端观测值,并重点关注受新冠疫情冲击后模型的估计。这里主要思考3个问题:第一,是否应该将疫情防控期间的极端冲击视为常规冲击;第二,极端冲击是否会扭曲模型的参数估计;第三,是否应该舍弃疫情防控期间的极端数据。由于疫情防控期间的数据会影响未来的时间序列观测值,而直接舍弃这种极端观测值低估了不确定性,因此舍弃后可能不利于对未来经济的预测。本文试图通过模拟冲击波动率的变化,刻画疫情防控期间异常大的经济不确定冲击。由于知道疫情导致经济不确定冲击增加的确切时间,因此可以对这些波动性变化进行建模,并通过贝叶斯方法来估计,以达到调整经济不确定性冲击规模的目的。Carriero等将冲击波动性设定为独立同分布过程[7],本文分阶段设定冲击规模,并将极端冲击后的波动设定为自相关过程,以刻画极端冲击后的波动衰退过程,这种设定也适用于波动性影响具有不对称性的情况。VAR模型设定如式(1)所示。

yt=C+B1yt-1+…+Bpyt-p+stεt,εt～N(0,∑)

(1)

其中,C是截距项向量,B1,…,Bp是系数矩阵,yt是n×1维的内生变量向量,εt是n×1维的简化冲击向量,st是用于调整极端冲击规模的残差协方差矩阵,stεt为模型的结构性冲击。假定极端冲击发生在t*时刻,在极端冲击开始之前st=1,在极端冲击开始后,根据实际观测数据设定相应预测误差的方差,st*=s(-)0,st*+1=s(-)1,st*+2=s(-)2,在此之后极端冲击以固定速度ρ衰减,st*+j=1+(s(-)2-1)ρj-2,其中θ≡[s(-)0,s(-)1,s(-)2,ρ]均是未知参数。在模型估计时常将上述VAR模型写成其一阶伴随形式,见式(2)。

Yt=Xtβ+stεt

(2)

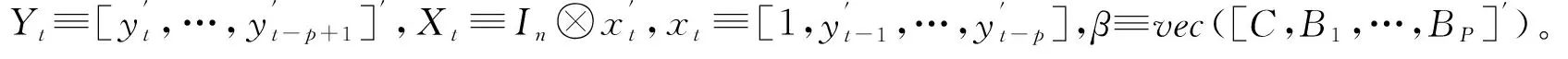
(3)

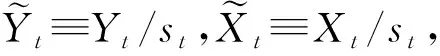
3 模型参数与超参数的先验设定

对于上述简化模型,首先设定参数的先验分布。考虑到方差的非负性,这里将简化冲击的方差协方差矩阵设定为逆威沙特分布,并将模型系数向量的条件分布设为正态分布。

∑～IW(Ψ,d)

(4)

β∣∑～N(b,∑⊗Ω)

(5)

本文将参数ψ、d、b、Ω均设定为超参数λ的函数,通过设定λ的取值即可确定参数ψ、d、b、Ω的分布,进而确定模型参数β和∑的先验分布,即分层建模。Giannone等提出了一种没有st的简化模型的估计方法[8],但在实际研究中,st通常未知,决定st演化过程的超参数γ和θ的联合后验分布见式(6)。

p(λ,θ∣y)∝p(y∣λ,θ)×p(λ,θ)

(6)

其中,y≡[yp+1,…,yt]′是样本观测数据,p(λ,θ|y)和p(y|λ,θ)×p(λ,θ)成比例关系。p(λ,θ)是超参数的联合先验分布,p(y|λ,θ)是模型的边际似然函数,则有:

(7)

其中,p(β,∑|γ)是超参数λ已知的条件下模型参数的联合分布。最后参考Giannone等的做法,将疫情冲击s(-)0、s(-)1、s(-)2的先验分布设为尺度参数和形状参数均为1的Pareto分布,将ρ的先验分布设为参数为0.8和0.2的beta分布。

4 数据来源及说明

本文共选择7个宏观经济变量:规模以上工业增加值累计同比增速(indus),从供给面反映经济增长状况;固定资产投资(不含农户)累计同比增速(inves),从需求面的投资上反映经济增长状况;社会消费品零售总额当期同比增速(retail),从需求面的消费上反映经济增长状况;进出口总额(美元)当期同比增速(trade),从需求面的进出口上反映经济增长状况;居民消费价格指数(上年同月=100)(cpi),用于反映通货膨胀状况;货币和准货币(m2)期末同比增速,从货币供应量上反映整体流动性;银行间隔夜同业拆借加权平均利率(shibor),通过短期拆借利率反映整体流动性。样本区间为2000年1月至2021年12月,共计264个样本点,数据来源于中经网统计数据库。对于上述指标中存在的个别缺失值,本文使用线性拟合法进行补充。

5 后疫情时期VAR模型的实证分析

结合超参数的后验分布来验证舍弃疫情防控期间的样本数据和直接将其当作正常值对待时,决定模型先验分布的超参数γ的分布情况,以此来证明Covid波动率设定的合理性,并进一步结合Covid波动率分布展示疫情暴发后冲击波动率的变动趋势。同时结合脉冲响应和密度预测,在实际应用中验证Covid波动率设定的现实意义。

5.1 超参数的后验分布

本文通过估计得到模型中超参数λ及θ≡[s(-)0,s(-)1,s(-)2,ρ]的后验分布(篇幅所限,结果备索)。其中超参数λ决定了模型参数的收缩程度,当只使用2019年12月及其之前的样本数据(不考虑疫情冲击的影响)估计模型得到的λ的后验分布,类似于Covid波动率(对疫情防控期间的极端冲击做特殊处理)下使用全样本数据估计得到的λ的后验分布,但是与固定波动率(不对极端冲击做特殊处理)下使用全样本数据估计得到的λ的后验分布差异较大,一定程度上说明本文对极端冲击情况处理方法的合理性。将疫情防控时期的观测值纳入估计样本,并将其当作常规数据来对待时,λ的分布向右偏移,这意味着模型参数的先验分布范围更广,这也是不考虑极端观测值所付出的代价。

使用全样本数据估计模型时使用的Covid波动率考虑了疫情开始时对经济造成的巨大冲击,这种影响会随着人们对该病毒的了解而降低,当人们从心理上不再恐惧时,即便同等程度的冲击,对经济造成的影响程度也不一样。后验分布中,s(-)0、s(-)1、s(-)2的后验峰值分别在2.7、1和3.8左右,表明2020年2月疫情刚发生时对经济的冲击大约是疫情前的2.7倍。随着封控政策颁布,疫情逐步趋于稳定,冲击标准差也逐渐降低,与疫情发生前基本持平。但随着越来越多的城市实施封控政策,疫情冲击程度也大幅上升,大约是疫情前的3.8倍。在此之后,疫情冲击以速度ρ进行衰减,ρ的后验峰值略低于0.95,表明自2020年5月以来冲击波动率每月大约下降5%。因此,直接将样本期间的冲击波动率设为固定值可能导致低估疫情带来的冲击,在分析经济变量之间的关系时将出现偏差,甚至得出错误的结论。

5.2 固定波动率下全样本数据的脉冲响应

图1是使用全样本数据估计模型但不对疫情冲击做特殊处理,并假定规模以上工业增加值累计同比增速上升1%得到的所有变量的脉冲反应及68%和95%的置信区间。不对疫情冲击做特殊处理相当于将疫情冲击期间的异常观测值看作正常观测值,理论上会影响模型的参数估计值,并最终影响脉冲响应结果。具体来看,规模以上工业增加值累计同比增速(indus)上升,这对于经济增长来说是正向冲击,反映出经济状况较好,经济增长明显。此时的固定资产投资(不含农户)累计同比增速(inves)、社会消费品零售总额当期同比增速(retail)、进出口总额(美元)当期同比增速(trade)和居民消费价格指数(cpi)均有上升,但上升幅度较小,反应的波动性也很小。面对经济的过快发展,货币和准货币(m2)期末同比增速下降,银行间隔夜同业拆借加权平均利率(shibor)上升,使得整体流动性下降。整体来看,系统内各个内生变量的反应具有一定合理性,但是由于图1使用全样本数据,并且未对疫情防控期间的数据做特殊处理,即假定为固定波动率,未考虑疫情带来的巨大冲击,导致整体反应较小,并且波动不明显。

图1 基于固定波动率下的全样本数据得到的脉冲响应图

5.3 固定波动率下部分样本数据的脉冲响应

图2是使用截至2019年12月的样本数据估计模型但不对疫情冲击做特殊处理,并假定规模以上工业增加值累计同比增速上升1%得到的所有变量的脉冲反应及68%和95%的置信区间。从中可以看出规模以上工业增加值累计同比增速(indus)上升,反映出经济状况较好,这种经济增长会在一年左右恢复至初始水平。从需求侧来看,固定资产投资(不含农户)累计同比增速(inves)会立即下降,然后逐渐恢复至初始水平,通常经济状况较好时固定资产投资也趋于上升,因此,这种不同于工业增加值变动的反向变化具有不合理性;从消费方面来看,社会消费品零售总额当期同比增速(retail)和进出口总额(美元)当期同比增速(trade)快速上升,随后很快恢复至初始水平,说明工业增加值的上升仅带来消费端的短期上升,由此带来的用居民消费价格指数(cpi)表示的通货膨胀上升也持续较短时间;从货币和准货币(m2)期末同比增速和银行间隔夜同业拆借加权平均利率(shibor)来看,工业增加值上升对整体流动性的影响也仅具有短期效应,但是二者反应的方向不尽合理,在经济状况较好时m2应该趋于下降而shibor趋于上升,图2的反应方向则相反。综上所述,由于图2直接忽略了疫情防控期间的样本数据,因此得到了不合理的脉冲响应图。

图2 基于固定波动率下的部分样本数据得到的脉冲响应图

5.4 Covid波动率下全样本数据脉冲响应

图3使用全样本数据估计模型,同时对疫情冲击的数据做特殊处理,并假定规模以上工业增加值累计同比增速上升1%得到的所有变量的脉冲反应及68%和95%的置信区间。在Covid波动率下,当工业增加值累计同比增速上涨一个百分点,反映出在经济状况较好的条件下,固定资产投资(不含农户)累计同比增速(inves)也上升,同时,社会消费品零售总额当期同比增速(retail)和进出口总额(美元)当期同比增速(trade)均上升。无论是供给侧还是需求侧均发展良好,反映在居民消费价格指数(cpi)上是有一定程度的通胀上升。在经济过热情况下,国家调控的结果就是整体流动性下降,因此货币和准货币(m2)期末同比增速下降,银行间隔夜同业拆借加权平均利率(shibor)上升,符合经济逻辑。通过图1、图2与图3的比较可以看出,本文对疫情防控期间异常冲击的处理,可以得到更加合理的脉冲响应图,也证明了本文方法的适用性。

图3 基于Covid波动率下的全样本数据得到的脉冲响应图

5.5 预测效果比较

使用截至2021年12月的数据分别估计Covid波动率模型和固定波动率模型。借助情景分析法,在工业增加值累计同比增速遵循顶部既定变化路径的条件下,分别基于两种模型对其余变量的变化趋势进行预测,得到2022年以来的后验中位数预测值及其68%和95%的置信区间(限于篇幅,结果备索)。通过对比分析发现,Covid波动率下的密度预测包含了更高的冲击方差,意味着疫情对我国经济未来前景的影响有更大程度的不确定性;而固定波动率下的密度预测区间相对更窄,究其原因是在模型估计过程中设置固定波动率而压低了波动程度。因此,在新冠疫情带来的不确定性增大背景下,Covid波动率下的密度预测是合理的。

基于上述研究发现,新冠疫情暴发导致变量出现异常观测值,在进行建模分析时直接删除这些异常观测值可能导致模型参数估计值偏误增加;而将疫情防控期间的异常观测值当作正常数据来对待同样不合适。本文通过分层建模方法拟合疫情防控期间的异常冲击变动趋势具有现实可行性,也为未来进一步开展经济问题研究提供了可供借鉴的方法。

6 研究结论与政策启示

本文基于宏观经济分析经常使用的VAR模型分析了异常观测值处理的必要性和具体方法,结合模型超参数λ及θ≡[s(-)0,s(-)1,s(-)2,ρ]的估计结果也可以看出,疫情发生以来各期的冲击波动率不一样且差异较大,直接将样本期间的冲击波动率设为固定值是不合理的。

本文通过对疫情防控期间的冲击波动率进行建模,分析了在工业增加值累计同比增速上升1%时其他宏观经济变量的脉冲响应,并对比分析了固定波动率下的脉冲响应结果。研究发现,使用全样本数据估计模型但不对疫情防控期间的数据做特殊处理时,得到的脉冲响应图波动不明显,原因在于低估了不确定性,最终导致不合理的经济变化趋势。若直接去掉疫情防控期间的数据且设定为固定波动率,固定资产投资(不含农户)累计同比增速、货币和准货币期末同比增速和银行间隔夜同业拆借加权平均利率会出现不合理符号。而使用全样本数据的Covid波动率设定下各变量的脉冲响应结果则符合经济学逻辑。

本文研究背景是新冠疫情暴发导致宏观经济变量异常波动,基于分层建模思想提出了针对异常冲击的建模方法和模型先验分布中参数的设定方法,降低了人为设定的主观性对模型参数估计的影响。本文方法也可以应用于其他包含极端观测值的情况,只要能够判断某时期的冲击波动性突然增加,且与正常时期的演变路径差异较大,并可能有一定的持续性,都可以使用本文方法,尤其是后疫情时期研究宏观经济问题时,更能凸显本文方法的优势。