单层1T-CoI2中Kitaev作用的第一性原理研究

朱凯 黄灿 曹邦杰 潘燕飞 樊济宇 马春兰 朱岩‡

1) (南京航空航天大学物理学院,南京 210006)

2) (南京航空航天大学,空天信息材料与物理工信部重点实验室,南京 210006)

3) (苏州科技大学物理科学与技术学院,江苏省微纳热流技术与能源应用重点实验室,苏州 215009)

1 引言

二维磁性材料具有独特的二维结构,优异的物理和化学性质,展现出了广泛的应用潜力,已经成为目前国际材料科学研究的前沿焦点[1-4].自从石墨烯被剥离以来,二维材料由于其多样化和有趣的特性而在纳米电子学中具有潜在的应用前景.其中,过渡金属化合物从二维材料家族中脱颖而出,由于一些材料具有内禀磁性表现出了更令人兴奋的特性.单层磁性材料作为二维材料家族中的一个重要成员,在自旋电子学方面的应用具有很大的潜力[5-9].对于范德瓦耳斯结合的大部分过渡金属的卤化物已经有了非常丰富的研究,如CrI3,CrCl3,NiI2,CoI2,CrTe2,VSe2,CrSe2等[10-16]都具有内禀磁性.目前,对于二维磁性材料的研究方兴未艾,其中对于磁性作用机制的探讨占据了很大一部分.

二维磁性材料中磁性原子间的作用机制,除了传统的海森伯相互作用(Heisenberg interaction,HBI),更丰富的磁性作用机制也可以得到充分展现.Kitaev[17]在2006年提出一个建立在六角晶格上严格可解的量子自旋液体模型——Kitaev模型.Kitaev模型很快就应用到真实材料中[18],α-RuCl3是其中的明星材料[19,14].事实上,已经有一部分Co基材料被研究,以此来寻找其中是否含有Kitaev作用,比如Na2Co2TeO6[20,21]和Na3Co2SbO6[22].最近,Xu等[23,24]通过第一性原理计算发现,二维单层材料含有重配位元素的正八面体结构,如CrI3,CrGeTe3,CrSiTe3等会存在Kitaev作用.CrI3和CrGeTe3是六角格子的晶格,其中的Kitaev作用来源于八面体重配位元素I和Te的自旋-轨道耦合(spin-orbit coupling,SOC)[23].由于单层1T-CoI2中的I和Te一样同属于重配位元素,也形成了包围Co原子的正八面体I笼子,所以有理由认为单层1T-CoI2里面也应该存在Kitaev作用.目前研究涉及到二维单层1T结构中的Kitaev作用非常稀少,因此表征单层1TCoI2结构中的Kitaev作用是一个值得深入探讨的问题.

Kitaev作用具有自身的作用规律,这些规律在自旋螺旋条件下,也可以呈现出来,为我们计算Kitaev作用奠定了基础.本文计算了单层1T-CoI2的能量E与波矢q的色散关系E(q).结果表明,体系基态呈现为反铁磁.进一步计算了考虑和不考虑SOC的色散关系,成功分离出了Kitaev作用和非对角项相互作用.有趣的是,Kitaev相互作用K项与非对角相互作用Γ的第一近邻作用参数分别为K1=0.64 meV,Γ1=1.09 meV,与海森伯相互作用的J′几乎处于同一数量级.因此,单层1T-CoI2可以作为Kitaev的备选材料,并且体系中的Kitaev作用占据了重要地位.

2 计算方法与理论模型

本文采用基于密度泛函理论第一性原理赝势平面波方法[25]的VASP软件[26]进行计算.VASP是一种基于密度泛函理论,利用平面波赝势来进行量子力学微观计算的软件,该软件通过平面波基矢量自洽迭代法求解密度泛函方程,并用波函数计算力和张量.由于VASP涵盖了元素周期表中大部分的赝势且赝势库较为成熟,同时又具有效率高、稳定性好以及准确性高等优点所以被广泛应用.到目前为止,VASP已经可以很好地应用于二维磁性材料的第一性原理计算[27,28].赝势采用VASP自带的Perdew-Burke-Ernzerhof势[29].VASP可以通过受力分析,根据牛顿第二定律,设置弛豫时间,逐渐让原子弛豫到基态上,力的收敛条件是0.01 eV.平面波截断能选取为368 eV,电子步自洽计算的总能量收敛标准为1×10-6eV.CoI2的晶格常数为3.92 Å[30].倒格空间的k点分布设置为15×15×1,运用半展宽为0.02 eV的高斯展宽进行弛豫和静态计算,并考虑体系的SOC作用.对于单层结构,增加了20 Å的真空区.为了解释过渡金属化合物中通常显著的相关效应,采用HubbardU修正[31,32]的简化形式,Co原子的有效U参数为3.3 eV[33],U为库仑排斥力.

在一些第一性原理计算中,磁性原子之间的交换耦合参数只考虑了最近邻原子之间的作用J1,并没有得到其他更远近邻间HBI磁交换能Ji[34-37].本文尝试计算到第8近邻耦合,同时考虑Kitaev相互作用的影响,并且尝试通过广义布洛赫条件,利用非线性计算方法计算了单层1T-CoI2的色散关系E(q).通过拟合E(q) 得到HBI的各个近邻Ji参数和Kitaev作用参数.为了描述相邻Co原子之间的相互作用,将其哈密顿量表示为

式中,第1项是Heisenberg线性作用(Heisenberg linear interaction,HLI);第2项是Kitaev相互作用K(Kitaev interactionK,KKI)与非对角相互作用Γ(Kitaev interaction Γ,KΓI).其中,Si,Sj是磁性原子归一化的磁矩;α,β,γ是磁性原子间键相关的磁矩方向.与之前的Heisenberg模型相比,本工作为了讨论方便,把铁磁基态能量作为参考点设置成0,磁矩旋转导致的自旋螺旋能量变化是与铁磁态相比较的绝对值.Jij,Kij和Γij是各相互作用的常数,cKij与cΓij分别是KKI与KΓI铁磁态时各作用项的值.

3 结果与讨论

3.1 原子结构与电子结构性质

单层1T-CoI2的经典晶体结构如图1(a),(b)所示.单层1T-CoI2的原子结构属于单层二卤化合物.一般情况下,该化合物是1T或2H的二维结构,它们分别对应于六角晶格和三角晶格的对称性.通过计算,单层CoI2的1T相能量为-8.7 eV,2H相的能量为-7.7 eV,单层CoI2的1T相的能量低于2H相,那么其基态结构就是1T相,符合Kulish和Huang[38]的计算.从图1(a)可以看出,每个CoI2由3个原子平面组成: 一层Co原子夹在两层卤素I原子之间,上下I原子所处的环境相同,可以用I1和I2表示.每个Co原子被6个相邻的I原子包围,形成一个八面体笼子.所以Co原子之间的相互作用可以看作正八面体笼子之间通过笼子边缘的传递的相互作用.

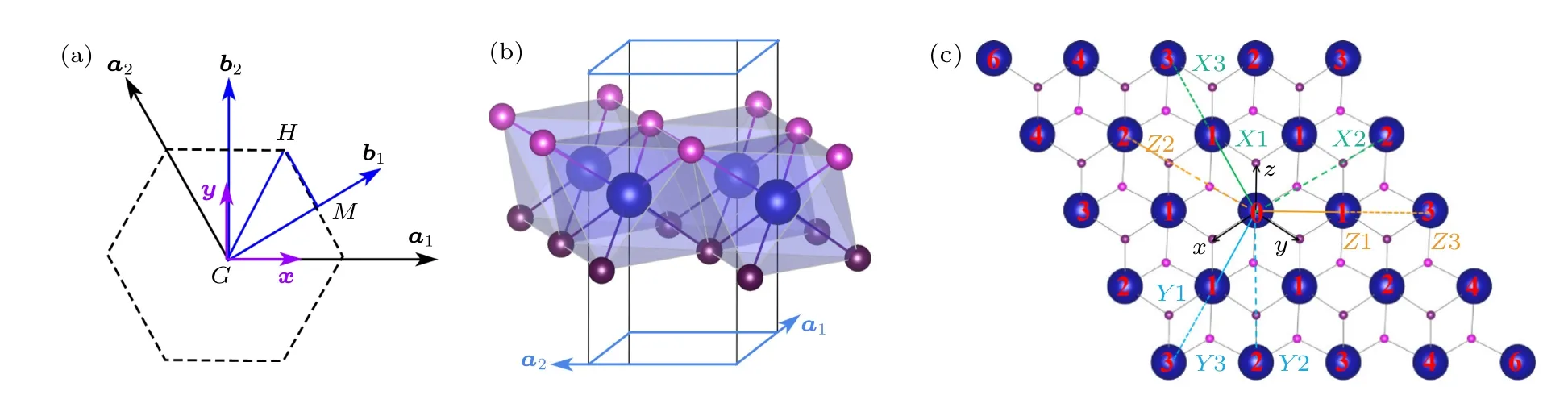
图1 (a)单层1T-CoI2的基矢图,其中a1和a2为基矢,b1和b2为倒格矢,G,M和H为第一布里渊区的高对称k点;(b)是单层1T-CoI2加上真空层后的原子结构侧视图,蓝色球、紫色球分别表示Co和I原子;(c)是扩展后5 × 5超胞俯视图,用来描述Co原子间HBI和Kitaev相互作用,以中间的Co原子为中心,红色数字表示Co原子的近邻位置.设置两个坐标系,[XYZ]表示的是Co—Co键,三角晶格上的第1近邻,第2近邻和第3近邻Co—Co键都标记在图中,绿色、蓝色和黄色分别表示X,Y和Z键.[xyz]表示相互垂直的3个Co—I键坐标系,其中x,y和z所表示的Co—I键分别垂直于X,Y和Z的Co—Co键所在平面Fig.1.(a) Base vector diagram of 1T-CoI2,where a1 and a2 are the base vectors,b1 and b2 are the reciprocal lattice vectors,G,M and H are highly symmetric k-points of the first Brillouin zone;(b) a side view of the atomic structure of 1T-CoI2 with a vacuum layer.The blue and purple balls represent Co and I atoms,respectively;(c) the top view of the expanded 5 × 5 supercell,which is used to describe the HBI and Kitaev interactions between Co atoms,centered on the Co atom in the middle,and the red numbers indicate the neighboring positions of the Co atoms.Two coordinate systems are set: [XYZ] represents the Co—Co bond,the first,second and third neighbor Co—Co bond on the triangular lattice are marked in the figure.Green,blue and yellow bonds indicate the X,Y and Z bond,respectively.[xyz] represents three Co—I bond coordinate systems perpendicular to each other,where the Co—I bonds represented by x,y and z are perpendicular to the plane where the Co—Co bonds of X,Y and Z are located,respectively.

Xu等[23]指出单层CrI3和CrGeTe3磁性的起源,是Kitaev作用与单离子各向异性作用共同引起的.两个系统中的各向异性交换能都是以Kitaev型为主,以单离子各向异性为辅.在后续的工作中,单层CrSiTe3经过压缩形变,可能存在量子自旋液体[24].如前所述,来源于自旋空间中各向异性的Kitaev相互作用造成单格点上的自旋阻挫[17],可以使系统进入到量子自旋液体态.这就大大扩展了可以产生量子自旋液体的材料选择范围.与α-RuCl3的SOC来自Ru离子4d轨道不同[39],CrI3和CrGeTe3的SOC都是通过配体重元素(CrI3的I或CrGeTe3的Te)p轨道的SOC而诱导的.在这两个结构中重元素配体都形成了包围磁性原子的八面体.这也指出了通过正八面体笼子传递磁相互作用的CoI2也会包含Kitaev作用.该Kitaev作用有多大? 是对角相互作用还是非对角相互作用? 都还需要进一步研究.

图1(c)是单层1T-CoI2原子结构的俯视图.为了标记出Co原子的不同近邻,将原胞扩展成5×5超胞.在俯视图1(c)中,中间的Co原子标记为Co0,距离Co0的第i个最近邻的Co原子用Coi表示,第1—第3近邻的原子个数各有6个,第4近邻原子个数是12个.Co原子间的Kitaev作用也标记在图中.其中,Co—Co键用XYZ表示,其中实线和虚线分别代表六角上的第1近邻、第2近邻和第3近邻.从原子结构来看,Co原子相互之间的主要包括HBI和Kitaev作用.

计算了U=3.3 eV,有无SOC条件下的单层1T-CoI2的电子结构.图2(a),(b)分别给出了铁磁状态下无SOC和有SOC的自旋相关电子能带结构.不考虑SOC时,费米能级稍微穿越价带顶,但考虑SOC后,费米能级则处于带隙中,该体系变成了半导体材料.这表明SOC在单层1T-CoI2中起到了重要的作用,可以导致由SOC引起的各种磁交换作用.这是考虑该体系的Kitaev相互作用的另一个切入点.单层1T-CoI2单层结构的各原子的态密度如图2(c),(d)所示.Co原子的上自旋和下自旋态密度分布有着明显的差异.并且原本没有磁性的I原子的上下自旋态密度在费米能级附近不再对称,而在-13 eV至-10 eV和4—8 eV处的上下自旋基本上下对称.因此I原子受到了磁性原子Co的影响,诱导出了部分磁矩,其大小为-0.05 μB,计算得到Co原子的磁矩为2.07 μB,所以磁矩的主要贡献是来自于Co.在费米能级附近,Co原子自旋向下的态密度更为明显,在-4 eV至-2 eV间的态密度主要是由上自旋产生,在费米能级处,Co原子产生了较大的态.

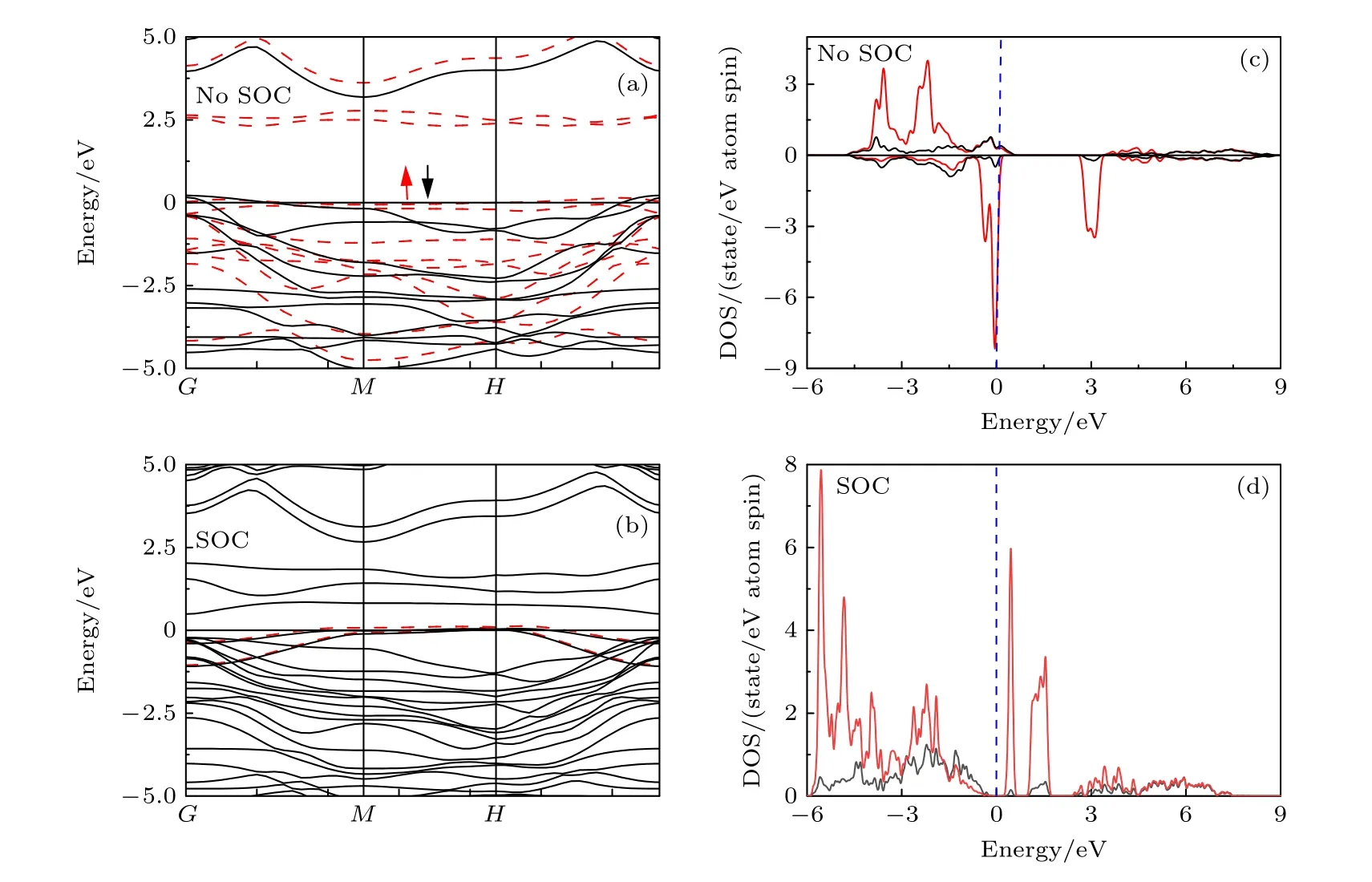
图2 (a),(b)单层1T-CoI2的能带结构,(a)中红色和黑色分别表示自旋向上和自旋向下的能带,(b)考虑SOC计算的能带图;(c),(d)单层1T-CoI2的态密度图,其中红色曲线表示Co原子,黑色曲线表示I原子,(c)为单层1T-CoI2的I原子和Co原子的分态态密度,纵坐标正值表示上自旋的态密度,负值表示下自旋态密度,能量为0处的蓝色虚线是费米面,(d)加SOC计算得到Co和I的总态密度图Fig.2.(a),(b) Band structure of the monolayer 1T-CoI2.The red and black lines in panel (a) indicate the spin-up and spin-down bands,respectively.(c),(d) Density of states (DOS) maps of monolayer 1T-CoI2,where the red and black curves show the DOS of Co and I atoms,respectively.In panel (c),positive and negative values indicate the DOS of the up and down spin,respectively;the blue dashed line at energy 0 is the Fermi level;panel (d) is the DOS of Co and I calculated with SOC.

3.2 自旋螺旋 E(q) 与Kitaev的计算

首先根据HBI和Kitaev的模型,推导出三角晶格中波矢为q的自旋螺旋能量与波矢的色散关系.如图1(b)所示,在三角晶格中,选择一个磁矩作为零点(命名为S(0)),位置j处的磁矩位置用Rj=ma1+na2表示.自旋螺旋的方向用q=q1b1+q2b2来描述.其中,a1和a2是基矢,b1和b2是倒格矢.在本文VASP计算中,所有的磁矩都设置在xy平面上,在广义布洛赫条件下,波矢为q的自旋波中,第j近邻的Co原子的磁矩S(Rj) 为

其中i和j是直角坐标系的单位矢量.将(2)式代入(1)式且在仅考虑第1—第8近邻的情况下,那么S(0)与第j近邻磁矩ES(q) 之间的HBI各分量EJi(q) 分别为

在不考虑SOC的时候,磁性原子间的磁交换作用为HBI,其色散关系以EN(q) 表示:

其中J1—J8为HBI参数并且包含S(0)2.

考虑SOC后,S(0)和S(Rj) 之间会存在Kitaev作用,其各近邻的线性项(作用参数为K,K项来源于垂直于Co-I-Co-I平面的Co电子之间的相互作用)和非线性项(作用参数为Γ,Γ项来源于平面内的电子间的交叉相互作用)分别如下:

各项的作用如图3所示,各个参量都设置为1,各参量在色散曲线中的作用如下: 在图3(a)—(c)中,Γ各项取1时,G点的能量值最低,正的Γ值会促进体系呈铁磁排布;在图3(d)—(f)中,K各项取1时,G点的能量最高,正值K的各项作用对反铁磁态有利.

图3 (a)只考虑Γ1=1时,EΓ1(q) 对应的色散关系图;(b),(c)分别是只考虑Γ2=1,Γ3=1时对应的 EΓ2(q),EΓ3(q) 色散关系图;(d)—(f)分别是K1,K2,K3取1时对应的 EK1(q),EK2(q),EK3(q) 色散关系图Fig.3.(a) Dispersion relation corresponding to EΓ1(q) when only Γ1=1 is considered;(b),(c) the corresponding EΓ2(q),EΓ3(q) dispersion relations when only Γ2=1 and Γ3=1 are considered,respectively;(d)-(f) plots of EK1(q),EK2(q),EK3(q) dispersion relations corresponding to K1,K2,and K3 taken as 1,respectively.

总的Kitaev作用EKitaev(q) 为

SOC引起的磁交换作用还应该包含短程的HBI,考虑到第3近邻,EKitaev(q) 之和与SOC下的HBI共同形成ES(q) :

体系总体的能量波矢色散关系是考虑SOC的和不考虑SOC色散关系之和EN+S(q) :

如图4(a)中黑色方框点所示,利用VASP计算了单层1T-CoI2考虑SOC的自旋螺旋的能量与波矢q之间的色散关系EN+S(q),其中,G点、M点和H点为图1(a)所示的第一布里渊区的高对称k点,它们的坐标分别是(0,0,0),(0.5,0,0),(1/3,1/3,0).根据(2)式,给定了波矢q,就能表达出不同位置的R上的磁矩,G点、M点、H点所对应的自旋螺旋结构分别如图4(d)—(f)所示.自旋螺旋q选取了第一布里渊区的边界KG-GMMK.可以发现,单层1T-CoI2的EN+S(q) 在最低点L时对应的q1=0.133;q2=0.133,所以体系的基态是图4(g)所示的自旋螺旋态,而不是图4(f)所示的线性反铁磁态[11].如图4(a)中的红色圆圈离散点所示,我们也计算了不考虑SOC的EN(q).EN(q) 几乎在各个q点都偏离了EN+S(q),也就是说SOC在单层1T-CoI2体系中起到了非常大的作用.根据(6)式两者之差ES(q) 也显示在图4(a)的蓝色散点中.ES(q) 都大于0,这表明SOC会导致磁矩呈现铁磁排布,但ES(q) 在每个q的绝对值都远小于EN(q),最终EN+S(q) 还是呈现螺旋反铁磁.

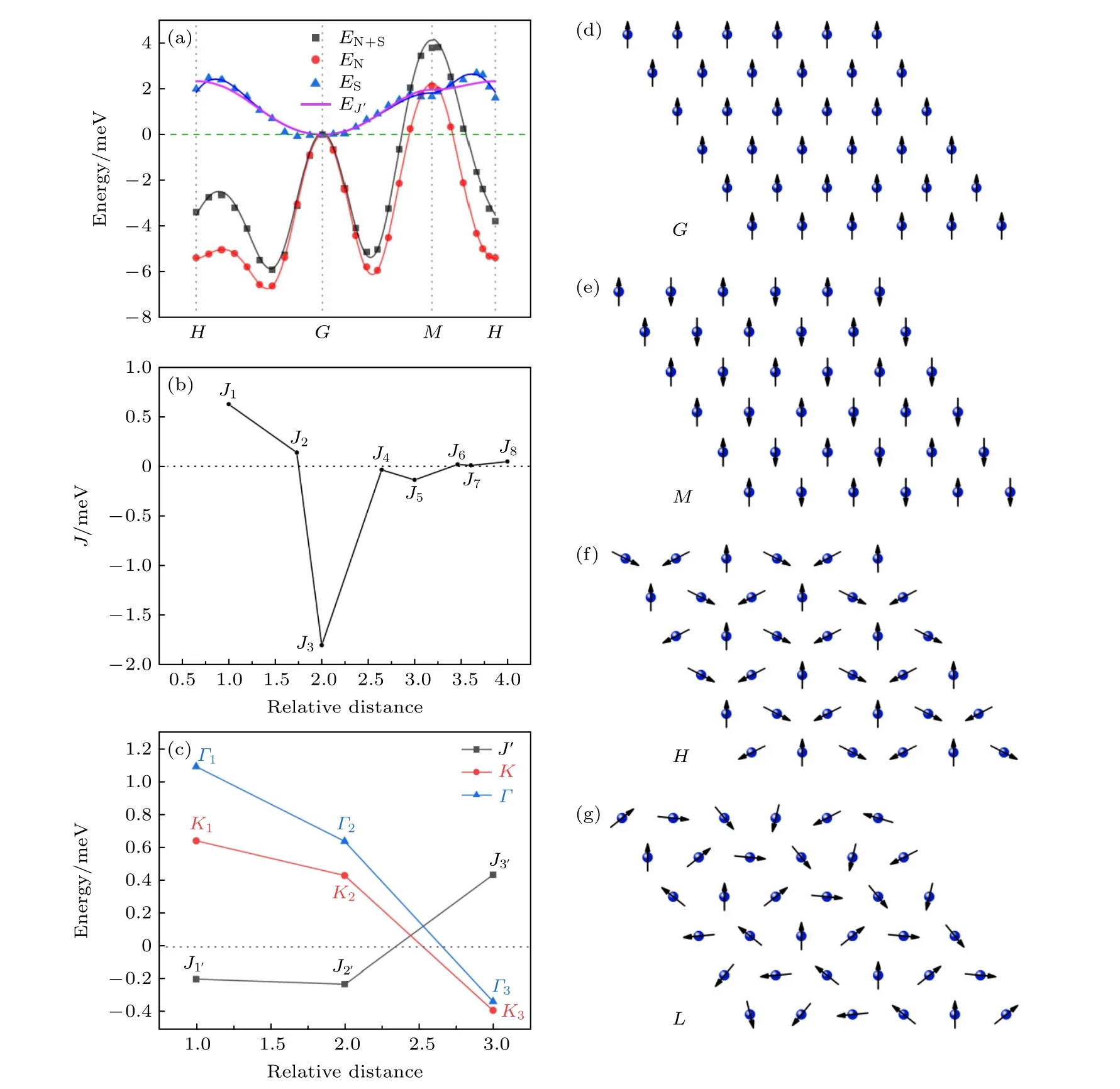
图4 (a)离散点分别代表的是计算的单层1T-CoI2体系的自旋螺旋能量与波矢q的色散关系 E(q),其中N表示不考虑SOC,S是只有SOC;黑色方框 EN+S 与红色圆圈 EN 是计算值,蓝色三角 ES 是两者之差.黑色曲线、红色曲线和蓝色曲线是对应的拟合曲线;H,G,M是图1(a)中第一布里渊区的特殊k点.(b)单层1T-CoI2中海森伯相互作用第1—第8近邻的J值变化趋势图.(c) SOC作用下第1近邻-第3近邻J,K,Γ参数点的变化趋势图.(d)—(g)表示第一布里渊区中H,G,M点和 E (q) 中最低点L的磁矩分布图Fig.4.(a) Discrete points represent the calculated dispersion relation E(q) between the spin spiral energy of the 1T-CoI2 system and the wave vector q.Among them,N means that SOC is not considered,and S means only SOC;the black box EN+S and the red circle EN are calculated values,and the blue triangle ES is the difference between the two.The black,red and blue curves are the corresponding fitting ones;H,G,M are special k points in the first Brillouin zone in Fig.1(a).(b) The J value of the first to eighth neighbors of the HBI in 1T-CoI2.(c) J,K,Γ parameter points from the first neighbor to the third neighbor with SOC.(d)-(g) Magnetic moment distribution diagrams of points H,G,M in the first Brillouin zone and the lowest point L in E(q).

ES(q)中是否像前文模型中分析的那样存在Kitaev作用,需要通过计算值拟合各参量来确定.首先,只用和来拟合计算ES(q),发现拟合的曲线与ES(q) 不能符合,如图4(a)中的紫色线所示.其中,J′已经随着距离收敛,加上的作用,与本身的色散关系无法完全表达离散点的色散关系.这表明,各向同性的HBI已经不能用来表述SOC导致的磁矩间的相互作用,必然有其他未知的磁性机制在起作用.根据上文对1T结构的分析,这种作用可以认定为是Kitaev作用.

EN(q)中可以完全用HBI的(3)式来拟合,拟合出的HBI参数如图4(b).通过J值图的变化趋势可以发现,单层1T-CoI2的J1=0.62 meV,Co-Co间为铁磁交换;而第3近邻的J3=-1.81 meV,为负值,但绝对值最大,之后呈现收敛趋势.这是单层1T-CoI2整体呈现反铁磁的主要原因.ES(q)中包含了由SOC引起的线性项和非线性项Kitaev作用.加入Kitaev作用后,图4(a)中根据(5)式拟合出的蓝色曲线与计算出的离散点ES(q) 符合得非常好.拟合出的K,Γ值显示在图4(c)中.可以看出K1=-0.64 meV,Γ1=1.09 meV,都大于最大,说明Kitaev作用在ES(q) 中占据主导地位.也说明三角格子的1T结构中同样含有Kitaev作用,且这个作用具有普遍性[23,24].K,Γ值随磁性原子间距离逐步减小.

4 结论

利用广义布洛赫条件计算了单层1T-CoI2的自旋螺旋色散关系.由于单层1T-CoI2的正八面体构型和重配位体在自旋螺旋耦合作用下会产生各向异性的键依赖作用,选择海森伯-Kitaev模型研究单层1T-CoI2的磁性相互作用.通过拟合自旋螺旋色散关系E(q),分别得到了HBI参数、Kitaev参数和非对角作用参数.单层1T-CoI2呈现出q为(2/15,2/15)的自旋螺旋态,主要贡献是J3.而在SOC作用下,证明了体系中存在各向异性的Kitaev作用,并且Γ1值为1.09 meV.我们推测Kitaev作用在1T结构三角格子中具有普遍性.基于广义布洛赫条件计算单层1T-CoI2的磁性基态并且结合自旋螺旋方法分析磁作用,为分析二维磁性材料的微观机制奠定了理论基础.计算结果不仅扩大了Kitaev材料的范围还为探索其他二维磁性材料的Kitaev作用提供了方向.