蛋白质pKa预测模型研究进展*

罗方芳 蔡志涛 黄艳东

(集美大学计算机工程学院,厦门 361021)

1 引言

为保证正常的生命活动,人体细胞的细胞质、细胞核以及各个细胞器需维持在特定的pH水平.例如,线粒体和溶酶体的pH分别是8.0和4.7,偏离细胞质的7.2[1].其中,用于表征溶液的酸碱度的pH为氢离子浓度的对数取负(pH=-log[H+]),其是人体中许多重要生物过程的调控因子,例如物质跨膜转运[2]、酶催化[3]、蛋白质折叠[4]、多肽聚集[5]、脂质分子自组装[6]、病毒入侵细胞[7]和细胞能量代谢[8].从微观的角度,以上生物过程均与关键可离子化基团的质子化(protonation)或去质子化反应(deprotonation)相关联.可离子化基团的去质子化(正反应)和质子化反应(逆反应): AH⇌A-+H+,其中,AH 是一种可离子化基团的质子化态,A-是去质子化态.

以β分泌酶BACE1为例阐述蛋白质功能和可离子化基团质子化/去质子化的关系.BACE1的生物功能是裂解β淀粉样前体蛋白APP.它与神经退行性疾病阿尔茨海默症密切相关,是典型的结构和功能依赖于pH的蛋白质.该蛋白的催化中心含两个天冬氨酸Asp32和Asp228 (图1(a)).实验指出,BACE1仅在一个狭小的pH范围内具有活性[9].如图1(b)所示,在最适pH条件下(约等于4.5),Asp32处于质子化态,扮演质子供体(proton donor);Asp228处于去质子化态,扮演亲核试剂(nucleophile).然而,当溶液pH偏离4.5,两个天冬氨酸同时质子化或去质子化,BACE1无法行使其生物功能[10].

图1 BACE1催化中心质子化态和功能的关系 (a) BACE1三维结构及其催化中心酸性二分体D32和D228;(b) D32和D228质子化态和蛋白质活性随pH的变化规律(D是Asp的缩写)Fig.1.Relationship between protonation state of BACE1 catalytic center and the function: (a) Crystal structure of BACE1 and the acidic dyad in the catalytic center;(b) protonation states of D32 and D228 and the activity as a function of pH (D is the abbreviation of Asp).

当一个可离子化基团的质子化和去质子化达到平衡,可由以下公式计算解离常数Ka:

其中,[H+],[A-]和[AH]分别代表溶液中氢离子以及该基团去质子化和质子化态下的浓度.Ka代表一种酸(如AH)离解氢离子的能力.将方程(1)的两边对数取负,可得到著名的Henderson-Hasselbalch方程:

其中,pKa为解离常数Ka的对数取负,代表一种酸(如AH)去质子化的难易程度.例如,溶液中天冬氨酸的 pKa测量值是3.7[11].根据(2)式,天冬氨酸在中性(pH=7.0)水溶液中处于去质子化态(A-);在pH小于3.7的酸性溶液中,天冬氨酸质子化(AH);当pH位于 pKa附近,质子化和去质子化态共存.如上所述,pKa决定了可离子化基团在任意 pH 条件下的质子化和去质子化反应平衡.根据 pKa值,可以推断不同 pH 条件下生物大分子质子化态的分布,进而讨论结构和功能的关系.因此,pKa是研究pH相关的生物化学过程的一个核心问题.不仅如此,pKa与药物研发中长期存在的靶向性和抗药性问题以及蛋白质设计密切相关.然而,由于蛋白质结构的复杂性以及实验条件的限制,人们难于通过实验获取蛋白质中可离子化氨基酸残基的 pKa,需借助理论预测.

为此,将以上Henderson-Hasselbalch方程转换为能量形式,得到游离氨基酸关于pH和 pKa的去质子化自由能 ΔGmod的表达式:

其中,kB和T分别是玻尔兹曼常数和温度;为游离氨基酸的 pKa,是可测量值.去质子化自由能可分解为成键作用部分 ΔGBond和非键作用部分ΔGNBond.其中,成键作用部分描述共价键断裂的能量变化,计算复杂度高,不适用于生物大分子体系[12].值得一提的是,当溶剂中的可离子化氨基酸参与蛋白质的合成,蛋白质环境对成键作用部分的影响可忽略不计.基于该假设,我们只需考虑非键作用部分.因此,可离子化氨基酸从溶剂到蛋白质的去质子化自由能改变量 ΔG-ΔGmod可表示为

根据(3)式,ΔGmod为已知量.因此,求解蛋白质中氨基酸残基的去质子化自由能 ΔG的问题简化为计算蛋白质环境对非键作用部分的自由能微扰.

基于以上框架,人们发展了基于自由能计算的蛋白质 pKa预测模型,例如恒定pH分子动力学(constant pH molecular dynamics,CpHMD)[13].许多生物大分子含有不止一个功能构象,并且构象的转变与质子化/去质子化反应相关联: 当活性位点质子化(pH ＜ pKa),蛋白处于构象C1;去质子化(pH ＞ pKa),构象由C1转变到C2;当pH取pKa附近,质子化和去质子化态共存,构象C1与C2相互转变.因此,只有考虑了构象与质子化态耦合的理论模型,才能得到和实验相一致的宏观 pKa(macroscopic pKa)[14].CpHMD通过分子动力学模拟实现在不同构象下对质子化态空间进行采样.在蛋白质 pKa预测精度方面,CpHMD相对其他现有模型具有明显的优势[15].CpHMD的缺点是 pKa计算效率低.例如,完成一个蛋白质 pKa的计算通常需要进行几个小时甚至几天的分子动力学模拟,因此难以满足工业界大批量计算的需求.目前,CpHMD多被应用于结构和功能依赖于pH的药物靶向蛋白的分子机制研究[16].

为了实现高通量的 pKa计算,人们发展了基于泊松-玻尔兹曼(Poisson-Boltzmann,PB)方程的模型,主要包括MCCE[17],H++[18],APBS[19],DelPhi-PKa[20]和PypKa[21].基于PB的模型能够在几分钟内完成一个蛋白质的 pKa计算,极大地提高了计算效率.然而,基于PB的模型具有其理论局限性.例如,由于连续介质假设,PB方程不适用于非水溶性的膜蛋白.其次,蛋白质结构的复杂性增加了介电常数的不确定性,因此即便是水溶性蛋白,分子内部(例如酶的催化反应中心)的 pKa计算对介电常数敏感[22].

除了以上基于能量的模型,人们也可以用一个经验函数描述某可离子化氨基酸残基的蛋白质环境(如疏水环境和氢键)与其 pKa偏移量的映射关系.蛋白质某氨基酸残基 pKa可表示为其游离状态下参考值和偏移量 ΔpKa的和:

2005年,基于前期的第一性原理计算工作[12],哥本哈根大学Jensen课题组[23]提出了一个计算蛋白质 pKa的经验函数PropKa.该模型提出一组经验公式分别计算库仑力、去溶剂化效应和氢键等关键因素对 pKa偏离参考值的贡献.PropKa可在几秒内完成一个蛋白质的 pKa计算,计算效率明显比基于PB的模型高,近20年得到了广泛的应用,其最新版本PropKa 3.0发表于2011年[24].

直到2021年12月,本课题组[25]发表了首个人工智能(artificial intelligence,AI)驱动的蛋白质 pKa预测模型DeepKa.随后,美国卡内基·梅隆大学Olexandr Lsayev、美国约翰斯·霍普金斯大学Ana Damjanovic和德国拜耳公司Pedro Reis研究小组陆续提出了基于机器学习的 pKa预测模型pKa-ANI[26],XGB-WMa[27]和PKAI/PKAI+[28].其中,DeepKa和PKAI/PKAI+主要依赖于数据集,而为了在少样本情况下建立有效模型,pKa-ANI和XGB-WMa需要一定程度的预训练或先验知识.值得一提的是,机器学习模型也能够在几秒内完成一个蛋白质的 pKa计算.

上述的CpHMD以及基于PB方程、经验函数和机器学习的模型是目前4种主流的 pKa预测方法.最近,本课题组[29]采用CpHMD扩增了pKa数据集,进一步提高了DeepKa的预测精度.值得一提的是,DeepKa已展现出类似物理模型(如CpHMD)的高鲁棒性,进一步证明了人工智能算法在蛋白质 pKa预测领域的有效性.下面将介绍这4种主流方法的理论基础及研究进展.

2 蛋白质pKa预测方法

2.1 CpHMD

根据质子化态采样方法的不同,恒定pH分子动力学CpHMD分为随机采样(discrete CpHMD,D-CpHMD)[30]和λ动力学(continuous CpHMD,C-CpHMD)[31].随机采样利用蒙特卡罗(Monte Carlo,MC)模拟在离散的质子化态空间(反应坐标取0或1)进行采样[30].λ动力学则采用取值范围0(质子化态)到1(去质子化态)的连续变量λ作为反应坐标对可离子化基团的电荷或体系哈密顿量进行标度[31].如图2所示,先使用以上基于MC或λ动力学的采样算法更新质子化态或者电荷.基于更新后的电荷分布,通过分子动力学模拟对构象进行采样.更新位置坐标后,进入下一轮质子化态的采样.模拟结束后,采用广义Henderson-Hasselbalch方程拟合CpHMD模拟产生的不同pH条件下某可离子化基团的去质子化概率S,进而获得其 pKa值,即S=0.5所对应的pH[31].

图2 CpHMD模拟框架Fig.2.Framework of a CpHMD simulation.

由于滴定动力学与构象动力学相关联,提高质子化态和构象空间的采样是近30年CpHMD模型发展的主线.下面将分别介绍D-CpHMD和CCpHMD.

2.1.1 D-CpHMD

D-CpHMD用一个反应坐标λ表示某可离子化位点的质子化态.λ只能取0或1.其中,0和1分别表示质子化态和去质子化态.经过一定长度的分子动力学(molecular dynamics,MD)模拟,随机选取一个可离子化基团,尝试改变其质子化态.例如,将其λ值从0改为1.然后,计算λ值改变引起的能量变化 ΔE.将该能量变化代入Metropolis准则:

如果能量差小于或等于0,接受λ值改变的概率为1.如果能量差大于0,则接受改变的概率p小于1.在数值模拟中,通常是随机生成一个取值范围为[0,1]的数s.只有s小于等于p,才接受λ值改变,否则保留原值.以上为一步的MC,和开始的MD构成一个模拟周期.因此,在MC之后,便是下一个周期的MD模拟.显性溶剂下质子化或去质子化的能量变化较大,导致较小的接受概率.起初,为了提高接受概率或质子化态的采样效率,MC的能量计算使用隐性溶剂(implicit solvent)模型,如广义玻恩(generalized Born,GB)[32-34]和引言提到的PB模型[31,35,36].当MC和MD均采用隐性溶剂,计算效率最高,但是牺牲了精度[32,33].为了提高构象方面的采样精度,MD可替换成显性溶剂,即杂化溶剂[31,34,35].其中,基于GB和PB的模型分别在分子模拟软件Amber和GROMACS中已被实现.需要指出的是,隐性溶剂难以描述活性位点附近与功能相关的水分子或盐离子对去质子化平衡的影响[37].

为提高显性水溶剂下MC的接受概率,2007年Stern[38]提出了尝试改变λ值之后,先进行一定长度的尝试性的分子动力学模拟,再计算能量差.该尝试性的MD使周围水溶剂构型得到调整,可降低λ值改变前后的能量差.然而,以上尝试性MD的长度依赖于经验或不确定,其应用可能受到限制.尽管如此,该模型为解决显性溶剂下质子化态空间的采样问题提供了一条新思路.随着高性能计算的发展,人们开始考虑将显性溶剂应用到蛋白质D-CpHMD的MC部分.如无特别说明,以下提到的显性溶剂均是分子动力学模拟中计算静电相互作用的标准算法PME (particle mesh Ewald,PME)[39].2015年芝加哥大学的 Roux课题组[40]提出了显性溶剂下的非平衡MD/MC模拟.例如,对于某可滴定位点在MC阶段的去质子化(λ由0变为1)尝试,该模型在0和1之间添加了m个中间值.对于每个λ值(m个中间值和两个边界值0和1),执行一定长度的非平衡MD,令可离子化基团周围的环境根据λ值在构型上作出调整,减缓了因λ值改变而导致的能量涨落.结束λ=1的非平衡MD后,计算当λ=1和λ=0的能量差.同样,根据Metropolis准则,如果接受该可滴定位点去质子化,继续λ=1的MD.否则,退回到非平衡MD前的时刻,继续λ=0的MD.通过以上的非平衡模拟,该模型提供了较合理的能量差的计算,提高了总体接受概率.Roux课题组[40,41]利用著名的Jarzynski方程将自由能变化与非平衡MD所做的功相关联,使得以上非平衡MD的模拟时间可被量化.值得一提的是,该方法可被应用于生物大分子,目前在分子模拟软件NAMD中已有实现.然而,可滴定氨基酸的固有 pKa(inherent pKa)是该模型的一个主要参量.为了提高预测性能,该模型要求固有 pKa尽可能接近真实值[41].因此,D-CpHMD一个潜在的研究方向是消除上述模型对固有 pKa的依赖.

2.1.2 C-CpHMD

本课题组统计了4057个蛋白质中可滴定氨基酸的个数[29].这些蛋白质来自复旦大学王任小实验室[42]创建的蛋白质抑制剂复合物数据库PDBbind的精细集v2016.除了半胱氨酸Cys,蛋白质中其他可滴定氨基酸类型(谷氨酸Glu、天冬氨酸Asp、赖氨酸Lys、精氨酸Arg、络氨酸Tyr、组氨酸His)的平均个数不低于10[29].理论上,一个含有N个可滴定氨基酸残基的蛋白质包含2N个质子化态.然而,D-CpHMD的MC每次只取一个可滴定位点来判断是否改变其质子化态,采样效率较低[34,43,44].

2004年,为了研究生物大分子体系(如蛋白质,DNA和RNA)的质子化和去质子化,密西根大学Brooks课题组开发了首个λ动力学框架下[45]的恒定pH分子动力学C-CpHMD[31].每个可滴定位点对应一个反应坐标λ,取值范围同样是0—1.和D-CpHMD不同的是,C-CpHMD的反应坐标是连续的变量.值得一提的是,C-CpHMD同时更新所有可滴定位点的质子化态.哈密顿量H代表体系的总能量,包括动能和势能.除了真实的粒子,如模拟体系中溶剂和溶质的原子,C-CpHMD添加了虚粒子.每个可滴定基团对应一个虚粒子.这里用范围在[0,1]的连续变量λ作为虚粒子的坐标.为了模拟虚粒子的滴定动力学,可将其质量设为10(单位是原子质量).以下是修正后的总哈密顿量:

其中,Natom是总粒子数,r是原子的位置矢量,λ是虚粒子的滴定坐标,ma和mj是原子和虚粒子的质量.第1和第4项的求和分别是原子和虚粒子的总动能.第2项Ubond是键相互作用能,包括键伸缩能、键角弯折能和二面角扭转能.这里假设键相互作用与λ无关.第3项Unbond是非键相互作用能,包括静电Uelec和范德瓦耳斯UvdW相互作用,与λ相关.最后一项U*是偏置势,利用经验势描述去质子化键断裂的能量变化,只和λ相关.

以下介绍如何利用λ标度非键相互作用能和偏置势.对于可滴定的氢原子和周围原子的范德瓦耳斯相互作用,直接用 1-λi标度势能函数(这里采用6-12勒让德琼斯势ULJ):

可见,当λ=1时,残基i去质子化,残基i的可滴定氢与j无相互作用.

对于两个可滴定氢之间的范德瓦耳斯相互作用,采用 1-λi和1-λj进行标度:

范德瓦耳斯力是近程非键相互作用力,主导疏水基团间的相互作用.然而,由于原子半径的差异,氢(半径约1 Å)几乎被与之成键(键长约1 Å)的重原子(半径约2 Å)包围,使其难以接触到其他原子.因此,质子化和去质子化对范德瓦耳斯相互作用影响不大,相对长程静电相互作用可以忽略不计.对于静电相互作用,λ标度的是原子电荷[31]:

早期为了提高计算效率,Brooks课题组[31]采用隐性溶剂模型计算溶剂对溶质的平均效应.如此一来,总静电能Uelec的溶质内静电相互作用仍采用库仑势((11)式第1项),而溶质与溶剂的静电相互作用Usolv采用GB势能函数((12)式):

其中,星号代表排除存在键相互作用的原子对;rab是电荷qa和qb的距离;εp和εw是蛋白质和水的介电常数;κ是德拜长度取反((13)式);I是盐离子强度;q是盐离子电荷;e是基本电荷;kB是玻尔兹曼常数;T是温度;α是有效玻恩半径,表征某原子埋在蛋白内部的程度,为衡量GB模型精度的关键参数.相对PB模型,GB的计算复杂度较低,并且是解析的,适合需要对位置坐标求一阶导(计算粒子所受合外力)的分子动力学模拟.GB模型的计算复杂度主要体现在有效玻恩半径的求解.

2004和2005年Brooks课题组接连开发了CH ARMM软件中基于隐性溶剂GBMV[31]和GBSW[46]的C-CpHMD,证明了基于GB的C-CpHMD在pKa预测方面的有效性.相对GBSW/GBMV溶剂模型,GBNeck2可提供更优的构象采样[47].于是,马里兰大学Shen课题组[48]在2018年开发了Amber软件中基于隐性溶剂GBNeck2的C-CpHMD.值得一提的是,对于实验科学家关心的酶催化中心(如图1活性位点Asp32和Asp228),该方法也表现较好,目前已被应用于共价抑制剂靶点的预测[49-51],蛋白质 pKa数据集的建立[25,29],以及依赖于pH的蛋白质分子机制研究[52,53].目前,基于GBSW和GBNeck2的C-CpHMD均已实现GPU加速,这进一步扩展了模型的应用范畴[54,55].

为了提高构象采样精度以及扩展C-CpHMD的应用范围,Shen课题组[56]提出了杂化溶剂CCpHMD: 构象动力学使用显性溶剂;而滴定动力学保留隐性溶剂.为此,构象动力学和滴定动力学采用不同的哈密顿量.前者去掉方程(7)的最后两项,第3项不再包含反应坐标λ,令方程(7)回归到常规分子动力学.该方法不仅维持了质子化态空间采样效率,而且提高了构象采样精度.起初人们会担心隐性溶剂GB的理论局限性(例如偏弱的疏水效应)会影响 pKa预测精度.然而,Shen课题组[56]发现,显性溶剂PME可导致偏高的疏水效应,一定程度上抵消了隐性溶剂导致的偏弱的疏水效应.相对隐性溶剂,该杂化溶剂C-CpHMD获得了广泛的应用,如钠离子质子交换蛋白[37,57],质子通道[58],类药物分子的膜渗透[59],芬太尼激活G耦联受体[60],糖苷水解酶[61],络氨酸激酶药物发现[62],以及上文提及的β分泌酶[10].

为了描述和功能相关的水分子或其他辅助因子(如金属离子和小分子)对去质子化平衡的影响,滴定动力学部分也需采用显性溶剂.起初,Brooks课题组和Shen课题组分别选择了较简单的基于截断的显性溶剂FSh (force shifting,FSh)[63]和GRF(generalized reaction field,GRF)[64].然而,由于截断,这两个模型均低估了长程静电力对可滴定位点的影响[65].为此,Shen课题组[66]开发了基于显性溶剂PME的C-CpHMD.最近,该模型在分子模拟软件Amber中实现了GPU加速[67].众所周知,PME是满足周期性边界条件(periodic boundary condition,PBC)的分子模拟中计算静电相互作用的标准算法,因此基于PME的C-CpHMD是λ动力学框架下所能达到的最优版本.理论上,如果不考虑取样问题,该模型的 pKa预测应该最接近实验.对于一个满足PBC的分子动力学模拟体系,PME的总静电能是3个能量项的加和:

其中,Udir是实空间静电相互作用,在库仑势基础上增加一个补偿函数,负责截断距离以内的短程静电相互作用((15)式).Urec最为耗时,为倒格空间(reciprocal space)下求解的长程静电能,负责截断以外的长程静电相互作用((16)式).Ucorr是修正项((20)式)[39].

其中,ra和rb是中心元胞的位置矢量;n是元胞的位置矢量,其表达式为n=n1c1+n2c2+n3c3,其中c1,c2和c3代表元胞的3个正交方向矢量;星号代表被排除的原子对,包括原子自身(a=b),形成化学键的原子对,以及最近邻(n的大小为1)以外的镜像;erf是补偿误差函数;参数β决定Udir和Urec的相对收敛速度.例如,β越大,Udir计算收敛越快,而Urec计算收敛会越慢.

式中m是倒格矢,其表达式为,其中,m1,m2,m3是非零整数;是以上ci(i=1,2,3)的共轭倒格矢,二者满足关系式=δij,这里i和j取1,2和3.另外,V=c1·c2×c3,是元胞的体积.S(m) 是结构因子:

该结构因子可近似表示为

式中通过将元胞中的电荷分布(B样条)插值到具有相同的3个维度k1,k2,k3的网格来构造三维矩阵Q;ki/Ki是分数坐标,其中,ki(i=1,2,3)取值范围是(1,2,3,···,Ki),正整数常数Ki代表元胞的尺寸;F(Q) 是矩阵Q的三维快速傅里叶变换.经过以上变换,Urec的表达式为

值得一提的是,Urec线性依赖于格点电荷,因此对λ求一阶导和库仑势的一样简单.

Urec考虑整体的电荷分布,并未排除存在键相互作用的原子对,因此需采用和Udir相同的函数形式进行修正((20)式第1项).此外,Ucorr第2项的作用是排除点电荷自相互作用,第3项则是中和体系净电荷的背景电荷(background plasma).其中,后面两个修正只依赖于原子电荷.

为了避免元胞之间不真实的静电相互作用,常规MD通过添加补偿盐离子使体系呈电中性.然而,CpHMD模拟中电荷是动态变化的.为了解决该问题,Shen课题组[64]提出了将盐离子作为质子缓存器.然而,盐离子如果不带电会导致聚集,于是改使用可滴定水分子[68].酸性氨基酸(例如Asp和Glu)与水阴离子(hydroxide,TIPU)耦合(AH+OH-⇌A-+H2O);碱性氨基酸(例如Lys,Arg和His)与水阳离子(hydronium,TIPP)耦合(BH++H2O⇌H3O++B).该耦合令反应式两端的电荷守恒.电中性的另一个好处是消除Ucorr中会导致反常 pKa偏移的背景电荷.

以上介绍了不同溶剂下静电能的具体求解.下面介绍哈密顿量中只依赖于反应坐标λ的偏置势[31]:

其中,第1项((22)式)和第2项((23)式)分别是游离可滴定氨基酸去质子化的非键相互作用能和总自由能.对于单个可滴定位点的氨基酸(如赖氨酸),Umod是一个关于λ的 一元二次函数.UpH由λ线性标度((23)式).UpH-Umod是化学能改变量的近似解.为了减少λ处于不真实的中间态(如λ=0.5)的概率,另外添加了一个二次函数势垒Ubarr((24)式).Ubarr降低了λ的动力学,对热力学统计没有影响.(23)式和(24)式的参数为已知,因此,C-CpHMD的主要工作是确定Umod的参数(如(22)式中的Aj和Bj):

需要注意的是,为了将λ约束在[0,1],需定义另一个变量θ.λ和θ的关系式为λ=sin2θ.于是,数值模拟中进行迭代的是θ,而非反应坐标λ.

对于含有两个可滴定位点的氨基酸,需要定义反应坐标x来描述处于去质子化(His)或质子化(Glu和Asp)态时质子所处的可滴定位点[46].x同样是在0到1范围内的连续变量.图3展示了Asp和His侧链3个质子化态对应的反应坐标值以及状态间的转化.类似变量λ,可利用插值将x加入哈密顿量的各个能量项.例如,以下分别是Asp和His电荷关于λ和x的表达式:

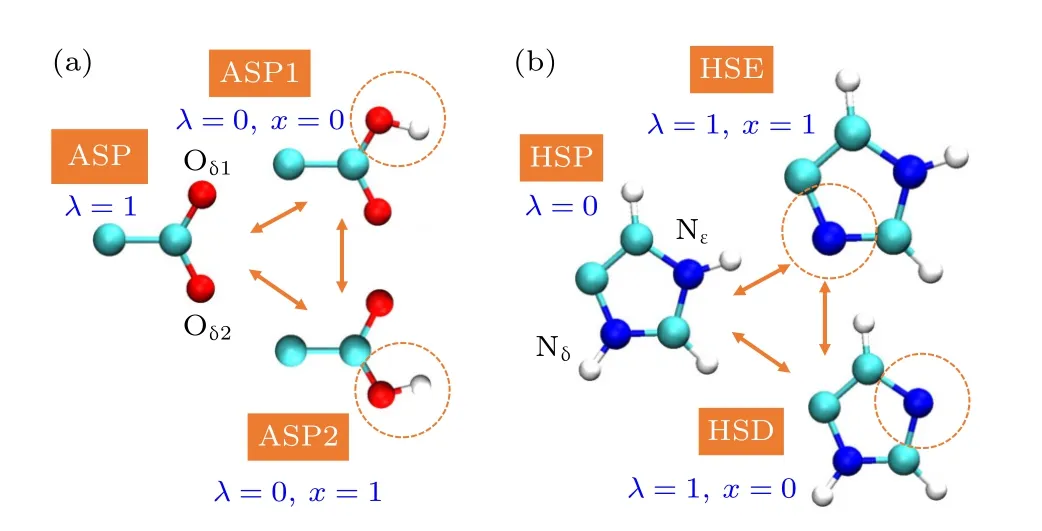
图3 互变异构滴定模型的3个质子化态以及状态间的转化 (a)天冬氨酸Asp;(b)组氨酸HisFig.3.Three protonation states and their interconversion in the tautomeric titration model: (a) Aspartic acid;(b) histidine.

CpHMD模拟同时对构象和质子化态采样.根据设置的输出频率保存每个可离子化基团的滴定坐标λ(λ∈[0,1])(图4(a)).统计处于质子化态(0≤λ≤0.1)的次数Nprot以及去质子化态(0.9≤λ≤1)的次数Ndep,计算不同pH条件下的去质子化概率S(图4(a))[31]:

图4 基于C-CpHMD的 pKa 计算 (a)滴定坐标λ和去质子化概率S的轨迹;(b)采用Hill函数拟合SFig.4.The pKa calculation based on C-CpHMD: (a) Trajectories of titration coordinate λ and deprotonation fraction S;(b) fitting S to Hill function.

最后,采用如下Hill函数(广义Henderson-Hasselbalch函数)拟合S.pKa便是S=0.5时所对应的pH (图4(b)):

其中h是Hill系数,表征一个可离子化基团与周围可滴定基团的滴定动力学是否存在耦合.h=1表示无耦合,如位于分子表面的残基或游离氨基酸.h＜1表示负耦合,如形成盐桥键的去质子化的Asp和质子化的Lys.h＞1 表示正耦合,如酶活性位点距离相近的两个酸性氨基酸(质子化的Asp或Glu).h偏离1越多,耦合越强[69].

当两个氨基酸的滴定动力学存在耦合,可将二者看作一个整体,利用以下公式计算宏观 pK1和pK2(macroscopic sequential pKa)[64,70]:

（2）边坡系数为1∶1的表层无覆土无植草边坡60min内的土壤流失质量1.31kg，15～20，20～25，25～30mm植生混凝土组的底部土壤流失量分别为0.0792，0.1089，0.1584kg；植生混凝土对底部土壤的反滤拦截率达86.92%。

其中N是一定pH条件下的平均质子数.为获得pK1和 pK2,也可以采用以下非耦合模型(31)式[71,72]:

其中S1和S2分别是两个耦合的可滴定位点的去质子化概率.

当滴定动力学采用满足周期性边界条件的显性溶剂时,需要考虑有限尺度效应[73].由于采用耦合水离子实现了电中性,有限尺度效应仅剩下和水分子模型相关的离散溶剂效应(discrete solvent effect)[66].当某个可滴定氨基酸去质子化,因离散溶剂效应引起的能量变化是

其中,κ是介电常数;ρ是水数量密度,等于水分子数N除以体积V,这里N指的是和蛋白有相互作用的水分子数,V也是这些水包络范围内的体积;q是可滴定氨基酸的电荷,Asp/Glu是-1e,His/Lys为+1e;γ是显性溶剂模型范德瓦耳斯相互作用中心的电四极矩.对于溶剂模型TIP3P,γ的值为 0.764e·Å2.为了估算该有限尺度效应导致的pKa偏移,需要计算相对模型分子的能量变化[66]:

其中,N和Nmod分别是蛋白质和游离氨基酸模拟体系中与溶质有相互作用的水分子数;V和Vmod是相应的周期性元胞体积.将以上表达式转化为pKa偏移量,可得到[66]

根据N和V的定义,可以推断有限尺寸效应对PME影响较大.PME考虑了周期性元胞内所有水分子,蛋白质体积所占比例较小,水数量密度ρ较大;另一方面,GRF和FSh仅考虑截断以内的水,蛋白质体积所占比例较大,水数量密度可忽略不计.对于膜蛋白体系,可参考Roux课题组[74]提出的方法做相应的修正.

以上介绍的C-CpHMD属于对电荷插值,实现电荷对反应坐标的线性响应.实际上,由于库仑势对电荷线性依赖,库仑势和电荷两者的线性插值是等效的.因为两种情况下,关于插值变量(反应坐标λ)负的一阶导数(作用在虚粒子上的合外力)是相等的.然而,并不是所有和静电势相关的能量项和电荷线性相关,如PME算法中对点电荷自相互作用和净电荷的修正项((20)式)[66].所以,为了更好描述电荷变化对滴定动力学的影响,基于截断的GRF和FSh较适合对静电势进行插值的CCpHMD,因为它们的静电势保留了对电荷的线性依赖.德国马克思普朗克研究所的Grubmüller课题组[75]在分子模拟软件GROMACS中开发的C-CpHMD便是对势函数进行插值.最近,芬兰的Groenhof课题组[76,77]基于该模型进行代码优化,并实现基于CHARMM力场的CpHMD模拟.然而,该模型采用了显性溶剂PME,而不是基于截断的GRF或FSh.其次,该模型没有像Shen课题组[64]一样考虑有限尺寸效应.另一方面,同样是对势能进行插值,Brooks课题组[63,71]基于显性溶剂的C-CpHMD模型合理地采用了基于截断的FSh.除了以上正弦函数形式,Grubmüller课题组和Brooks课题组提出了其他将λ约束在区间[0,1]的方法.例如,Grubmüller课题组[75]提出了余弦形式.Brooks课题组[78]提出一个较复杂的指数形式.对于显性溶剂C-CpHMD,体系电中性是一项重要的约束条件,Shen课题组[66]和Grubmüller课题组[79]均采用了可滴定水分子实现体系净电荷恒等于0.然而,Brooks课题组[71]的显性溶剂C-CpHMD还未考虑该约束.因此,为了避免溶质与其镜像的静电相互作用,需对FSh静电势设置较小截断值.

随着显性溶剂CpHMD的快速发展,急需解决质子化态和构象的采样问题.2006年Brooks课题组[82]率先将基于温度的副本交换(replica exchange)算法应用到C-CpHMD,即将副本以一定的概率交换到较高温度,借助热涨落提高CpHMD模拟的采样.受到哈密顿量副本交换算法的启发,2011年Shen课题组[56]提出了基于pH的副本交换算法: 将副本以一定的概率p交换到较高的pH,提高去质子化态的采样;或交换到较低的pH,提高质子化态的采样((35)式).因为实际进行交换的pH只存在于UpH((23)式),交换前后总能量的变化Δ/β可简化为仅含UpH的表达式((36)式).交换pH后,两个副本将在新的pH条件下(或新的UpH)进行采样.该算法效率极高,同时操作简单,已被应用到其他CpHMD模型[83-86].为了增强质子化态空间采样,美国国立卫生研究院NIH的Brooks课题组[87]提出结合包络分布采样(enveloping distribution sampling,EDS)和哈密顿量副本交换(Hamiltonian replica exchange,HREX).EDS通过定义一个参数s标度状态间的能垒.较小的s对应较平滑的能垒,方便了状态间的转化.然而,能垒的消除促进了虚拟中间态的采样,这将影响物理态的采样.为了避免中间态的采样,在EDS基础上利用HREX提高离散的质子化态空间的采样效率.接着,该课题组[86]加入以上基于pH的副本交换,构成二维的副本交换.从算法的角度,该方法确实提高了采样效率,但代价是产生大量的副本以及模拟过程中副本的频繁通讯,对计算能力要求较高.近期,为了在有限GPU显卡数量的条件下实现基于pH的副本交换,Shen课题组[88]提出了副本同步交换.

其中,p是副本交换的概率;UpH({λj};pH) 和是两个副本交换前的UpH.将以上两项的 pH和pH′进行互换,得到UpH({λj};pH′) 和.

除了副本交换,另一种增强采样的方法是对生物大分子进行粗粒化(coarse graining,CG),减少模拟体系中粒子的数量,从而降低了构象空间的自由度.该方法通常被应用于具有较大空间和时间尺度的生物过程,如蛋白质折叠、多肽聚集和物质跨膜转运等[89].近几年,研究者们开始将CG与CpHMD结合,发展CpHMD的粗粒化模型[90-93].值得一提的是,提出Martini粗粒化力场的Marrink课题组[92]已在分子模拟软件GROMACS中实现了CpHMD的粗粒化模拟.

2.2 基于PB的 pKa 预测模型

实际上,如果只考虑单个结构,可以用PB方程计算相对去质子化自由能 ΔΔG=ΔG-ΔGmod.其中,ΔGmod是某可离子化氨基酸A在游离状态下去质子化自由能改变量:

式中Gmod(A-)和Gmod(AH) 分别是去质子化(A-)和质子化(AH)状态的自由能.同理,当该氨基酸参与蛋白质的合成,它在蛋白质中的去质子化自由能改变量 ΔG表示为

基于蛋白质环境不影响成键作用部分ΔGBond(见(4)式)的假设,以上两个自由能改变量的差可表示为

其中,下标PB表示用PB方程分别计算等式右边4个状态下的静电能.令ΔG(AH)=GPB(AH)-,可得到

其中,ΔGPB(AH)和ΔGPB(A-) 分别表示在水溶剂中将质子化(AH)和去质子化(A-)的氨基酸放入蛋白质的静电能改变量.基于该等式,可以得到如图5所示的热力学循环(thermodynamic cycle).相对去质子化自由能 ΔΔG 可表示为

图5 相对去质子化自由能计算的热力学循环Fig.5.Thermodynamic cycle of relative deprotonation free energy calculation.

接着,将 ΔΔG代入关系式ΔpKa=ΔΔG/(kBTln10)计算 pKa偏移量 ΔpKa.最后,利用(5)式计算 pKa.可见,热力学循环4个状态的静电能计算决定了pKa的预测精度.目前,基于PB计算静电能并预测蛋白质 pKa的方法包括MCCE[17,94],H++[18],APBS[19],DelPhiPKa[20,95,96]以及PypKa[21].其中,MCCE和PypKa利用MC对侧链二面角进行采样,一定程度上提高了预测精度,但总体精度仍低于CpHMD,说明了空间构象充分采样的重要性[15].PB方程的参数主要是介电常数,原子的电荷和半径,因此容易拓展到其他类型的体系.例如,除了蛋白质,DelPhiPKa也适用于DNA和RNA.除了蛋白质单体,H++也考虑了含有配体的复合物.

2.3 基于经验函数的 pKa 预测模型

以上物理模型(CpHMD和基于PB的模型)需要计算体系的静电能,计算复杂度较高.为了进一步提高 pKa计算的效率(例如将单个蛋白的pKa计算时长缩短到秒量级),2005年哥本哈根大学的Jensen课题组[23]提出了一组经验函数PropKa分别描述点电荷相互作用(Coulomb force)、去溶剂化效应(desolvation)和氢键相互作用(hydrogen bonding)对 pKa偏移量的贡献:

以上3项的函数均采用分段的一次函数,计算复杂度低,已被应用到蛋白质单体[23],蛋白质和小分子配体的复合物[97].然而,该版本的PropKa没区分可滴定氨基酸残基是处于蛋白质的表面还是内部.

为此,2011年Jensen课题组[24]提出了改进的PropKa 3.0.新版本考虑了相同的 ΔpKa决定因子,将(42)式的氢键相互作用导致的和去溶剂化效应导致的归为自能不同的是,PropKa 3.0采取了一个折中的方案,即部分使用能量公式.例如,点电荷相互作用采用经典的库仑势.去溶剂化效应采用了和GB模型中求解有效波恩半径的倒数(1/α)类似的原子体积(V)除以原子间距离的四次方(r4).此外,蛋白质表面和内部被赋予不同的介电常数.对于氢键相互作用,则保留了一次函数形式.该模型的参数化基于谷氨酸和天冬氨酸的 pKa实验值,对酸性氨基酸的预测能力接近CpHMD[98].然而,该模型对碱性氨基酸(如Lys和His)的预测效果较差[25].

2.4 基于机器学习的 pKa 预测模型

上述PropKa经验函数的提出较大程度依赖于科学家的先验知识.理论上,如果有足够多的pKa实验测量值,可以结合数据和机器学习算法训练出一个经验函数,而不需要依靠已有的知识.2018年 波兰华沙大学Siedlecki课题组[99]提出首个基于深度学习的蛋白质配体结合亲和性(binding affinity)预测模型.这里的配体通常指具有几何结构的小分子.我们知道,pKa表征某可滴定基团去质子的难易程度.换一种表达,pKa代表蛋白质和质子的结合亲和性.可见,蛋白质配体结合亲和性预测方法对 pKa预测具有参考价值[25].

由于实验条件的限制,迄今为止蛋白质可滴定氨基酸残基的 pKa实验测量值不到两千个[100,101].于是,本课题组采用基于隐性溶剂GBNeck2的CCpHMD[48]建立了一个蛋白质 pKa数据集(包含12809个 pKa)[25].2021年12月,本课题组提出了国际上首个基于机器学习的蛋白质 pKa预测模型DeepKa,证明了引入人工智能方法解决蛋白质pKa预测问题的可行性[25].本课题组对现有的pKa数据库PKAD[100](包含1350个蛋白质 pKa实验测量值)进行数据清洗,得到了测试集EXP67S.首先,根据氨基酸序列相似性比对排除了冗余数据.剩下的67个蛋白质的470个Asp,Glu,Lys或His的 pKa构成数据集EXP67.接着,对EXP67进行欠采样,使得不同 ΔpKa区域分布均匀.最后剩下的167个 pKa为该模型的测试集EXP67S.该测试集的优势将在下文的多模型比对体现出来(图6).模型的大部分输入特征以及三维卷积神经网络(convolutional neural network,CNN)框架均借鉴Siedlecki课题组[99]提出的Pafnucy模型.值得一提的是,为了解决截断导致的边界问题,DeepKa采用格点电荷(Siedlecki课题组[99]采用原子电荷)描述对 pKa预测精度起决定性作用的静电环境[25].虽然DeepKa第一版本的预测精度高于PropKa 3.0,但是和CpHMD还存在一定差距[25].此外,该工作只测试了DeepKa的总体性能,并未对特定的问题(如酶催化中心或无序蛋白)进行讨论.

图6 pKa预测模型性能对比Fig.6.Comparison of existing pKa predictors.

2022年1月,美国卡内基·梅隆大学Lsayev课题组[26]开发了基于神经网络势ANI-2X和原子环境矢量AVE的深度学习模型pKa-ANI.然而,该模型将所有的实验数据用于模型的训练,不利于对其性能进行客观的评价.另外,该模型对结构敏感,需要在预处理阶段对初始结构进行能量最小化,否则将得到不合理的预测结果[26].2022年3月,美国约翰斯·霍普金斯大学Damjanovic课题组[27]测试了4种基于树的机器学习算法.其中,XGB-WMa表现最好.该小组同样采用有限的实验数据来训练和测试模型.为了建立有效的模型,他们在特征描述上加入了较多的经验知识: 首先,统计可滴定基团参与的氢键数量;其次,计算可滴定基团的溶剂可及表面积(solvent accessible surface area,SASA);最后,根据是否带电或亲水对可滴定基团附近氨基酸残基进行分类.显然,以上特征基本上覆盖了PropKa模型中影响 pKa偏移量的3个关键因素:氢键相互作用、去溶剂化效应和点电荷相互作用.2022年7月,Reis课题组[102]利用基于PB的Pyp Ka建立了包含1200万个 pKa值的数据集,并基于该数据集开发了深度学习模型PKAI[28].为了提高精度,在PKAI基础上对损失函数进行正则化处理,从而得到PKAI+.然而,PKAI+在其他测试集(如EXP67S)的表现与PKAI相似,说明上述的正则化处理缺乏普适性[29].因此,如果没有特别说明,下文只讨论PKAI.

2023年5月,本课题组发布了DeepKa的最新版本[29].该版本的输入特征和模型框架与旧版本相同,仅仅是增加了训练和验证集的 pKa样本量.这些样本出自549个蛋白质的26552个Asp,Glu,Lys和His.相对旧版本,该版本预测性能更接近CpHMD.此外,在这个工作中特定的蛋白质体系被用于进一步评估DeepKa的可靠性.例如,酶催化中心具有复杂的静电环境,是 pKa预测的一个重要挑战.新版本通过 pKa计算准确预测了5个酶催化中心的质子供体.除了具有稳定三维结构的蛋白,该模型也可被应用于无序蛋白.理论预测pKa偏移量较小的滴定位点往往容易做到预测精确,但难以做到预测相关,而即使在 pKa偏移量小于1.0的情况下,理论和实验仍然表现出较高的相关性,证明了该模型的高鲁棒性[29].如无特别说明,下文的DeepKa代表该新版本.

上述基于AI的模型均采用PKAD中的实验数据来训练或测试模型.然而,pKa-ANI,XGBWMa和PKAI忽略了存在于PKAD的冗余数据(例如一个蛋白质有两组相同的 pKa值),这可能导致过拟合.其次,PKAD中大多数 pKa处于参考值附近,因此测试结果并不能反应模型真实的预测能力[25].值得一提的是,本课题组创建的测试集EXP67S不存在以上两个问题,可较为客观地对模型进行评价[25].研究发现,除了在实验和理论相关性方面仍旧低于CpHMD,DeepKa的预测精度明显高于其他主流 pKa预测模型,包括PypKa,PropKa,PKAI和pKa-ANI[29].其中,PypKa代表基于PB的模型,PropKa代表基于经验函数的模型,PKAI和pKa-ANI代表其他AI模型.基于树的XGB-WMa没有开放源代码,所以无法利用EXP67S对其进行测试.因此,XGB-WMa不参与下面的模型讨论.同时考查精度和速度,图6展示了5个模型的预测性能.其中,平均绝对误差用于表征模型的精度.显而易见,如果以PropKa的速度和CpHMD的精度作为参照,目前只有DeepKa能提供准确的高通量 pKa计算[29].最近,加拿大国家研究委员会Sulea课题组[103]比较了现有的7种高通量 pKa预测模型,包括基于经验函数的PropKa 3.0[24],基于深度学习的DeepKa[29]、PKAI和PKAI+[28]以及基于PB方程的DelPhiPKa[95]、MCCE2[94]和H++[18].该研究指出在以上高通量模型中DeepKa的精度最高,与图6的结论一致.

3 结论

pH与温度、压强一样是基本的环境参量.传统的分子动力学假设溶剂是中性水(pH=7.0),不考虑其他pH条件;此外,传统分子动力学假设电荷是固定的,不受溶质静电场的影响.以上两个假设限制了传统分子动力学进一步探究细胞中许多与pH相关的生物过程,而可靠的 pKa计算将有助于解决该难题.本综述主要介绍了4类主流的pKa预测方法.显然,对于不同理论的 pKa预测模型,其适用范围也存在差异.首先,不论何种特定的问题,如果不要求高通量计算,可采用预测精度较高但计算效率较低的CpHMD.当涉及非水溶性蛋白(如膜蛋白)的 pKa计算,目前理论上可行的模型为基于杂化溶剂[37,56]或显性溶剂[66,67]的CpHMD.另一方面,需要开发高通量的 pKa预测模型,从而满足工业界批量的 pKa计算需求.由于隐性溶剂的理论局限性和实验条件的限制,上述的高通量模型仅适用于水溶性蛋白.对于水溶性蛋白质单体的pKa计算,在所有高通量模型中DeepKa无疑是最优的选择[29,103].若只关心酸性氨基酸残基(如Asp和Glu)的质子化态,也可考虑PropKa 3.0[24].而对于主要的4种可离子化氨基酸残基(Asp,Glu,Lys和His)以外的可滴定基团(如Cys和Tyr),可考虑基于PB的模型(如H++[18]和PypKa[21]).

随着计算机软件和硬件的快速发展,国际著名的美国药物设计公司薛定谔(Schrödinger)开始尝试利用自由能微扰(free energy perturbation,FEP)方法计算 pKa,说明蛋白质 pKa理论计算开始引起工业界的关注[104].值得一提的是,基于机器学习的pKa预测模型虽处于起步的阶段(2021年至今),却已表现出和物理模型同水平的预测精度,例如本课题组开发的DeepKa.我们相信: AI模型有可能突破先验知识,在不久的将来提供更为高效的预测;利用物理模型CpHMD建立的 pKa数据集PHMD549和基于 pKa数据库PKAD建立的测试集EXP67S将为基于机器学习的 pKa预测工具的研发奠定基础[29].最近,基于DeepKa本课题组开发了国内首个蛋白质 pKa在线计算平台(http://www.comput biophys.com/DeepKa/main),这对未来参与到人工智能驱动的新药研发产业具有重要意义[105,106].