层间共价键和拉伸应变对双层石墨烯纳米带热导率的调控*

2024-01-06李耀隆李哲2李松远张任良2

物理学报 2023年24期

李耀隆李哲2) 李松远张任良2)†

1) (燕山大学建筑工程与力学学院,秦皇岛 066004)

2) (燕山大学,河北省重型装备与大型结构力学可靠性重点实验室,秦皇岛 066004)

1 引言

石墨烯是一种由碳原子经过sp2杂化形成的单层蜂窝状的二维材料[1],由于其优异的机械[2]、电子[3]和热学[4]方面的性质而受到了广泛关注.石墨烯由于其具有极高的载流子迁移率,因此它在微电子设备中应用越来越广泛[5,6].随着电子器件不断的集成化和小型化,石墨烯纳米器件需要有效的散热来确保其使用性能和寿命,这促使人们需要对石墨烯的热输运性质进行深入研究.2008年,Ghosh等[7]使用非接触式拉曼光谱的方法首次通过实验方法对石墨烯的热导率进行测量,测得其热导率在3080—5150 W·m-1·K-1之间.随后学者们通过实验、理论计算、分子动力学模拟等方法对石墨烯的热输运性质进行了大量的研究,发现石墨烯的热导率受长度[8]、宽度[9]、边界手性[10]、温度[11]、基底[12]等多种因素的影响.

随着工业的快速发展,理想的石墨烯无法满足其应用的需要.因此,功能化的石墨烯受到了越来越广泛的关注.功能化会对石墨烯的热传导性能产生重要的影响.Chien等[13]通过非平衡分子动力学方法研究了氢化对石墨烯纳米带热导率的影响,发现氢化率为2.5%时石墨烯的热导率就降低了40%.Pei等[14]通过非平衡分子动力学也研究了氢化对石墨烯热导率的影响,得到同样的结论.杨平等[15]研究了氮参杂对石墨烯热传导性能的影响,发现随着氮原子浓度的增加,石墨烯的热导率逐渐降低,同时氮原子参杂位置也会影响石墨烯纳米带的热导率.

除单层石墨烯外,多层石墨烯也备受人们的关注.研究发现,给双层石墨烯施加一个横向的门电压可以使两层碳原子出现势能偏差,从而可以打开石墨烯的带隙[16].同时,石墨烯层间范德瓦耳斯相互作用、层与层之间声子弱耦合机制[17]对其面内热导率产生重要影响[18].实验和理论研究表明[19,20],石墨烯的面内热导率随着层数的增加逐渐递减,其原因是由于层间的范德瓦耳斯相互作用限制了石墨烯的自由振动,并阻碍了声子沿平面方向的输运.但是,在一些特殊的结构中,当层间的范德瓦耳斯相互作用受限时反而导致其热导率升高,如Yu等[21]通过平衡态分子动力学模拟发现,通过特殊的堆叠方式,能够使石墨烯纳米带以及聚乙烯的热导率提高两倍以上.对于双层石墨烯,研究发现,通过高温高压[22]、电子辐照[23]、飞秒激光[24]、化学反应[25]等方式,能够改变双层石墨烯中碳原子的杂化方式,使层间局部碳原子由sp2杂化转变为sp3杂化,即双层石墨烯层与层之间形成共价键.这些层间共价键可以在层间形成强烈的跨平面耦合,影响双层石墨烯的电学、力学和热学性质.Rajabpour和Vaez Allaei[26]通过分子动力学方法研究了双层石墨烯随机分布的层间sp3键对其热导率的影响,发现随着sp3键浓度的增加,双层石墨烯的热导率逐渐减少.Guo等[27]研究了石墨烯层间sp3键沿纵向和横向分布对其热导率的影响,横向分布的sp3键对双层石墨烯的热导率影响更大,最高可使其热导率降低80%.层间共价键不仅可以调控纳米结构面内的热导率,对界面间的热导也有重要的影响[28,29].Chen等[30]研究了层间共价键对多层石墨烯层间热阻的影响,发现多层石墨烯的层间热阻随着层间共价键的浓度增加呈现先升高后下降的趋势.Fan和Yao[31]研究了层间共价键对石墨烯/六方氮化硼异质结构界面热导的影响,发现层间共价键会显著降低其界面热导.文献[32,33]通过分子动力学模拟,研究发现通过碳链的键合能够使石墨烯纳米带层间的界面热阻降低一个数量级,并采用声子弱耦合模型[17]对其热输运机理进行了分析和解释.

层间共价键对双层石墨烯热导率调控的研究虽然取得了一些进展,但是层间共价键的分布对热导率的影响,以及相应的调控机制还不清楚.本文使用非平衡分子动力学方法,研究了呈链状分布的层间共价键对双层石墨烯纳米带热导率的调控.重点分析了层间共价键链的浓度和角度对热导率的调控,同时还研究了层间共价键和拉伸应变耦合作用对双层石墨烯纳米带热导率的调控.研究结果对石墨烯基纳米器件的热传输和热调控有一定的意义,有利于新一代微纳米电子器件的发展.

2 模拟方法

本文建立的模拟系统为具有链状分布的层间共价键的双层石墨烯纳米带,如图1所示.通过改变两层石墨烯中X,Y坐标相同的两个原子之间的法向距离,使它们之间的距离由3.4 Å变为1.6 Å,来形成局部层间共价键.为了使整个体系的能量最低,保证模型的稳定性,在建模时保证每个原胞中的两个碳原子最多只有一个碳原子能够形成层间共价键.模型共包含两层石墨烯纳米带,石墨烯纳米带的尺寸为19.96 nm × 5.12 nm,由3840个碳原子组成,石墨烯纳米带X方向的边界为锯齿形.在模拟的过程中,将Y方向设置为周期性边界,以避免尺寸效应对计算结果的影响,将X和Z方向设置为自由边界.

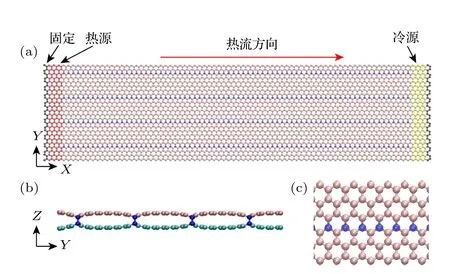
图1 (a) 非平衡分子动力学模拟模型图;(b) 模型侧视图;(c) 模型的局部放大图Fig.1.(a) Model diagram of non-equilibrium molecular dynamics simulation;(b) model side view;(c) model partial enlarged view.

使用大规模开源的分子动力学软件LAMMPS进行模拟[34].在模拟的过程中,使用多体AIREBO势函数描述石墨烯面内和层间的碳-碳共价键的相互作用[35];使用12-6型的Lennard-Jones对势描述石墨烯层间的范德瓦耳斯相互作用,势阱深度取2.968 meV,原子间的平衡距离取0.3407 nm,截断半径设置为1.02 nm[36].

使用非平衡分子动力学方法进行热导率的模拟,在模拟的过程中,沿热流方向将模型左右两端的两列原子固定,以防止其与外界产生热量交换.将模型左端的六列原子设置为热源,右端的六列原子设置为冷源,如图1所示,模拟的时间步长设置为0.5 fs.在模拟过程中,首先使用共轭梯度法对整个系统进行能量最小化,以保证模型整体结构的合理性.然后在正则系综(NVT)下,使用Nose-Hoover控温方法将系统的温度控制在300 K,进行0.5 ns的弛豫.弛豫完成之后,将系统切换为微正则系综(NVE),通过交换热源和热汇之间的能量,从而使模型沿X方向产生热流,然后在该系综下运行0.5 ns使系统达到动态稳定;将系统沿X方向平均分成40份,再将系综在微正则系综下运行0.5 ns,统计每个原子的温度,并通过对每个区域原子的温度进行时间平均和空间平均,得到系统沿X方向温度的分布,如图2所示.温度越高分子热运动越剧烈,通过对系统进行温度敏感性分子动力学模拟,发现当温度超过550 K时,层间共价键开始发生断裂,因此,为了保证模型结构的稳定性,模拟时控制热流大小使热源的最高温度不超过500 K.

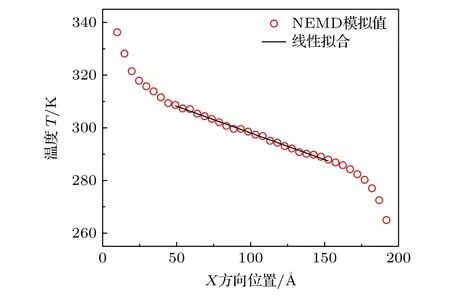
图2 模拟系统的温度沿X方向分布Fig.2.Distribution of temperature in the X-direction of the simulation system.

取温度场中间的线性部分进行线性拟合,得到X方向的温度梯度,然后通过傅里叶热传导定律即可计算出系统的热导率:

其中k为热导率;为沿X方向的温度梯度;J为热流密度,即单位时间流过石墨烯界面单位面积的能量.为了解释层间共价键对双层石墨烯热导率的影响,计算了其声子态密度(phonon density of states,PODS).其中PDOS是通过对原子的速度自相关函数(velocity autocorrelation function,VACF)进行傅里叶变换得到

其中vi(t) 表示第i个原子在时间t时的速度;N为计算声子态密度是所用到的原子数;t为关联时间;ω为频率,由于VACF为归一化和无刚量化的,所以ω的单位为 THz-1.

3 结果与分析

为了验证模拟设置和模型的可靠性,首先对单层和双层石墨烯纳米带的热导率进行了模拟计算,模拟的石墨烯尺寸为19.96 nm × 5.12 nm,计算得单层石墨烯纳米带和双层石墨烯纳米带的热导率分别为125.6 W·m-1·K-1和117.2 W·m-1·K-1,模拟结果与文献[14,26]相近,但是远低于实验测量的结果,主要是由于石墨烯的声子平均自由程为775 nm,受计算机计算量的限制,模拟的石墨烯尺寸远小于其声子平均自由程,其热导率具有明显的尺寸效应[37].同时模拟结果也表明双层石墨烯纳米带的热导率低于单层石墨烯纳米带的热导率,与Wei等[20]的研究结论一致,其原因主要由于石墨烯层与层之间声子弱耦合机制对其面内热导率的影响[17,18].双层石墨烯纳米带与单层石墨烯纳米带的不同之处在于,双层石墨烯考虑了层间范德瓦耳斯相互作用,可见即使这种弱相互作用,也会影响双层石墨烯面内热导率,而对于相互作用能较强的层间共价键对双层石墨烯纳米带热导率的影响,以及背后的物理机制接下来将重点讨论.

3.1 层间共价键的浓度对双层石墨烯纳米带热导率的调控

首先研究了层间共价键链与热流方向平行时,层间共价键的浓度对双层石墨烯纳米带热导率的影响.层间共价键浓度定义为石墨烯层内形成层间共价键的原子数与整个层内所有原子数量的比值.图3给出了不同层间共价键浓度的双层石墨烯纳米带示意图,其中层间共价键链与热流方向平行且等间距分布,分别计算了具有1,2,4,6列层间共价键的双层石墨烯纳米带的热导率,其层间共价键的浓度分别为2.08%,4.16%,8.33%,12.5%.图4即热导率随层间共价键浓度的变化曲线,可以看出,随着层间共价键浓度的增加,热导率逐渐降低.具体而言,理想的双层石墨烯纳米带热导率为117.2 W·m-1·K-1,当层间共价键的浓度为12.5%时,热导率为72.9 W·m-1·K-1,下降了38%.这与Guo等[27]的研究结果相似.根据声子的散射机制很容易得出原因: 层间共价键浓度的增加,一方面会导致声子的散射作用增强,另一方面,层间共价键浓度的增加也会导致模型的声子群速度和声子平均自由程减小,从而导致热导率降低[14,38].

图3 不同层间共价键浓度的模型图 (a) 层间共价键浓度为2.08%;(b) 层间共价键浓度为4.16%;(c) 层间共价键浓度为8.33%;(d) 层间共价键浓度为12.5%Fig.3.Snapshot of model diagram of different interlayer covalent bond concentration: (a) interlayer covalent bond concentration of 2.08%;(b) interlayer covalent bond concentration of 4.16%;(c) interlayer covalent bond concentration of 8.33%;(d) interlayer covalent bond concentration of 12.5%.

为了进一步探究层间共价键导致双层石墨烯纳米带热导率降低的原因,使用(2)式和(3)式计算了不同层间共价键浓度的双层石墨烯纳米带面内和面外PDOS,以及同一模型中共价键区域和非共价键区域的PDOS,如图5所示.从图5(a)即面内PDOS可以看出,在中低频区(0—40 THz),层间共价键对面内PDOS的影响不大,不同共价键浓度的双层石墨烯声子谱几乎重合,在40—54 THz的范围内,随着层间共价键浓度的升高,PDOS有所升高.相对于低频峰,层间共价键对于面内PDOS的高频峰(G峰)影响较大,随着层间共价键浓度的升高,面内PDOS的G峰出现了明显的红移,且G峰的峰值逐渐降低.G峰的红移和降低,导致了声子模式的软化,从而加剧了声子间的散射作用,导致热导率的降低.同时,G峰的红移和降低,也说明了声子群速度以及声子平均自由程的降低[39,40],其进一步导致双层石墨烯热导率的降低.

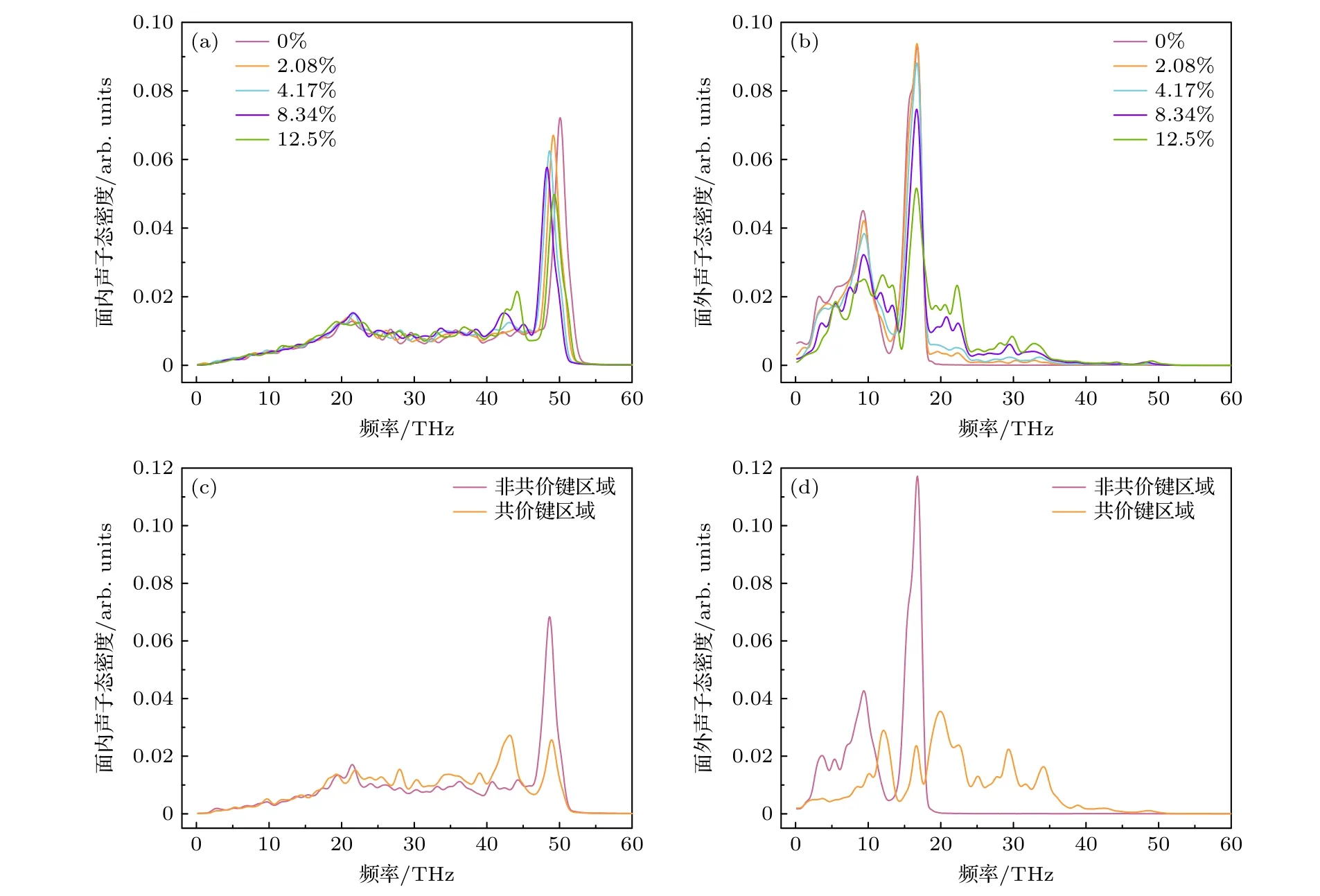
图5 (a) 不同层间共价键浓度的双层石墨烯的面内PDOS;(b) 不同层间共价键浓度的双层石墨烯的面外PDOS;(c) 相同模型共价键区域和非共价键区域的面内PDOS;(d) 相同模型共价键区域和非共价键区域的面外PDOSFig.5.(a) In-plane PDOS of bilayer graphene with different interlayer covalent concentration;(b) the out-plane PDOS of bilayer graphene with different interlayer covalent concentration;(c) the in-plane PDOS of covalent and noncovalent bond regions in the same model;(d) the in-plane PDOS of covalent and noncovalent bond regions in the same model.

图5(b)给出了不同层间共价键浓度的双层石墨烯纳米带的面外PDOS.从图5(b)可以看出,在低频阶段(0—20 THz),面外PDOS两个低频峰的峰值随着层间共价键浓度的增加而下降,但是在两个峰值之间的区域,面外PDOS的值随着层间共价键浓度的升高而增加.在大于20 THz的高频区,随着层间共价键浓度的增加,面外的PDOS被激发了更多的峰,说明更多声子通道被激发,从而导致更多的沿面内传输的声子转变为面外声子,导致双层石墨烯面内热导率降低.

从图5(c)的不同区域的面内PDOS可以看出,与非共价键区域相比,共价键区域的G峰出现了明显的红移,同时分裂成了两个峰,说明在共价键区域发生了强烈的声子散射,而非共价键区域的G峰则比较完整.从图5(d)的面外PDOS可以看出,共价键区域面外PDOS的截止频率远高于非共价键区域,同时在共价键区域,更多的特征峰被激发,说明层间共价键导致更多的沿面内传输的声子转变为面外声子.综上看出,层间共价键只对石墨烯纳米带局部的声子输运产生影响,因此,当层间共价键链与热流方向平行时,随着层间共价键浓度的增加,热导率逐渐降低.

3.2 层间共价键链的角度对双层石墨烯纳米带热导率的调控

接下来研究了层间共价键链的角度对双层石墨烯纳米带热导率的影响.层间共价键链的角度定义为共价键链与热流方向之间的夹角.图6为层间共价键浓度为4.16%时,层间共价键链呈不同角度的双层石墨烯纳米带示意图,无论何种方向分布,层间共价键链均沿其垂直方向呈等间距分布.分别计算了层间共价键链与热流方向呈0° (平行),30°,60°,90° (垂直)时,具有不同层间共价键浓度的双层石墨烯纳米带的热导率,如图7所示.从图7可以看出,无论何种分布,双层石墨烯纳米带的热导率均随着层间共价键浓度的增加而减小,减小的程度与共价键链的角度相关.具体而言,当双层石墨烯纳米带层间共价键链与热流方向平行时(共价键链呈0°),如3.1节所述,其热导率随层间共价键浓度的增加逐渐减少,在相同浓度下,相对于其他共价键链角度的双层石墨烯的热导率,减小的幅值最小.当双层石墨烯纳米带层间共价键链呈90°分布时,在相同浓度下,相对于其他共价键链角度的双层石墨烯纳米带的热导率,减小的幅值最大,并且随着层间共价键浓度的升高,其热导率减小的幅值变化很小,例如浓度仅为2.08%的层间共价键已使得双层石墨烯纳米带的热导率降低了62%,而当层间共价键浓度增加到12.5%时,其热导率也仅降低了67%.当双层石墨烯纳米带层间共价键链呈30°或者60°分布时,随着层间共价键浓度的增加,这两种共价键链角度的双层石墨烯的热导率变化的规律相似,并且在相同浓度下,这两种角度分布的双层石墨烯的热导率减小的幅值比共价键链呈0°分布的情况大,比共价键链呈90°分布的情况小.例如当层间共价键浓度为2.08%时,层间共价键链呈30°分布的模型,热导率降低了43%,层间共价键链呈60°分布的模型,热导率降低了40%.

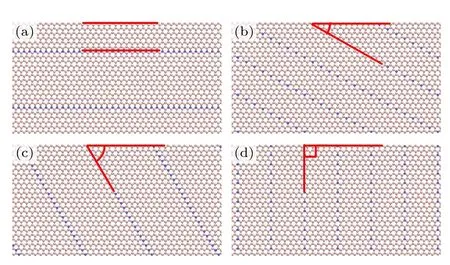
图6 层间共价键链呈不同角度时的模型图 (a) 层间共价键链呈0°;(b) 层间共价键链呈30°;(c) 层间共价键链呈60°;(d) 层间共价键链呈90°Fig.6.Snapshot of model diagram of interlayer covalent bond chain at different angles: (a) 0° interlayer covalent bond chain;(b) 30° interlayer covalent bond chain;(c) 60°interlayer covalent bond chain;(d) 90° interlayer covalent bond chain.

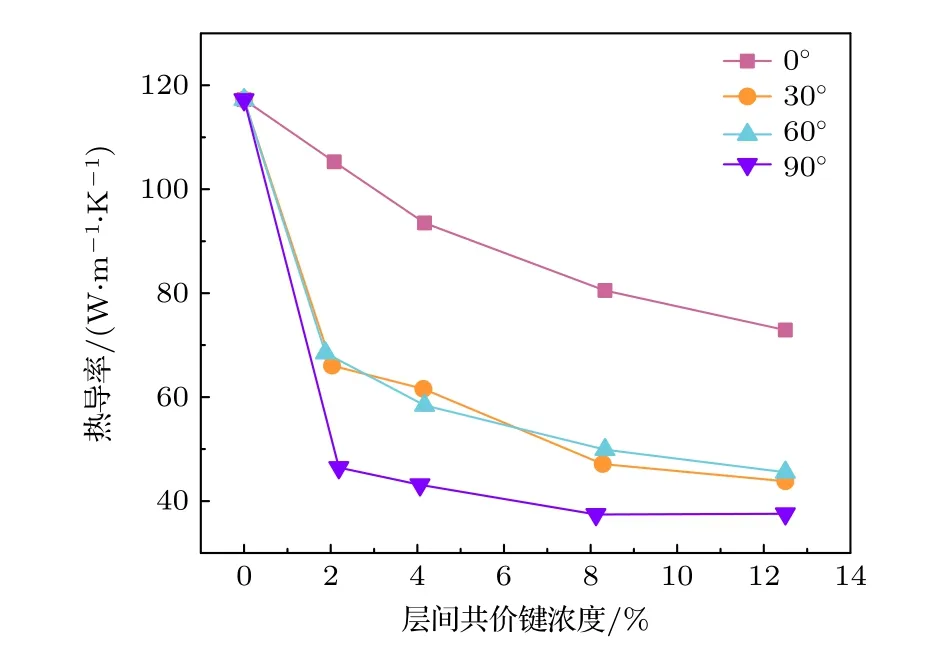
图7 层间共价键链的角度以及浓度对热导率的影响Fig.7.Influences of the angle and concentration of the covalent bond chain on thermal conductivity.

层间共价键链角度分布对双层石墨烯热导率的影响可能是由以下因素导致的.当层间共价键链与热流方向平行时,沿热流方向的热输运通道逐渐受到影响,部分的声子发生了散射,随着层间共价键浓度的增多,越来越多的声子输运受到了影响,故热导率随着层间共价键浓度的增加单调下降.当层间共价键链呈90°时,在层间共价键链处会形成界面热阻,在此处发生强烈声子-界面散射现象[41,42],所以即使浓度很小的层间共价键,也能对整体的热流输运产生很大程度的影响.当层间共价键链呈30°或者60°时,层间共价键链附近会形成界面热阻,导致声子散射,从而导致热导率减小.

3.3 拉伸应变和层间共价键耦合作用对双层石墨纳米带烯热导率的调控

通过拉伸应变可以改变纳米结构的热传输性质[43-46],如16%的拉伸应变会导致锯齿形的石墨烯纳米带热导率降低77%,导致扶手型的石墨烯纳米带热导率降低56%[43];12%拉伸应变会导致碳纳米管-氮化硼纳米管异质结构的热导率降40%[44];而对于特殊的结构,比如Mo6S6纳米线,拉伸应变反而会导致其热导率升高[45].因此,有必要探究拉伸应变对具有层间键合的双层石墨烯纳米带热导率的影响.首先计算了完整的双层石墨烯纳米带的热导率随拉伸应变的变化趋势,发现双层石墨烯纳米带的热导率随拉伸应变的增加呈近似线性下降,当拉伸应变为10%时,热导率下降了43%,与文献[43]的结论基本一致.

层间共价键和拉伸应变耦合作用对双层石墨烯纳米带热导率的影响如图8所示,为了使得拉伸应变对热导率的影响更为清晰显示,图中的热导率为相对热导率,即该模型受到拉伸应变时的热导率与其原始的热导率的比值.图8(a)为层间共价键链与热流方向平行时,不同层间共价键浓度下,热导率随拉伸应变的变化趋势.结果表明,对于具有层间共价键的双层石墨烯纳米带,其热导率随拉伸应变的增加而减小,10%的拉伸应变使其热导率降低了40%左右,这与拉伸应变对理想石墨烯热导率[43]和碳纳米管-氮化硼纳米管异质结构热导率的影响[44]基本一致.在相同的应变情况下,层间共价键浓度越大的模型,其受拉伸应变的影响越小,热导率下降的越少.热导率对应变的依赖性主要是受声子散射和声子群速度的影响,为了对其进行更好的解释,研究了不同层间共价键浓度的双层石墨烯纳米带在不同拉伸应变下的声子态密度,如图9所示.从图9可以看出,无论何种层间共价键浓度的双层石墨烯纳米带,随着应变的增加,面内PDOS的G峰出现了明显的红移,同时峰值也逐渐降低,甚至高浓度的模型中,较大的拉伸应变使得G峰分裂为了两个峰[47].这导致了声子模式的软化,说明声子间的散射作用增强,从而降低了声子的弛豫时间,导致热导率降低;同时也表明声子群速度的降低,进一步导致了热导率的降低.这与Wei等[39]研究的石墨烯热导率对应变依赖性的结论一致.从图9也可以看出,随着拉伸应变的增加,面内PDOS的中频段(20—40 THZ)有更多的峰被激发,进一步说明了拉伸应变导致声子散射的增加.

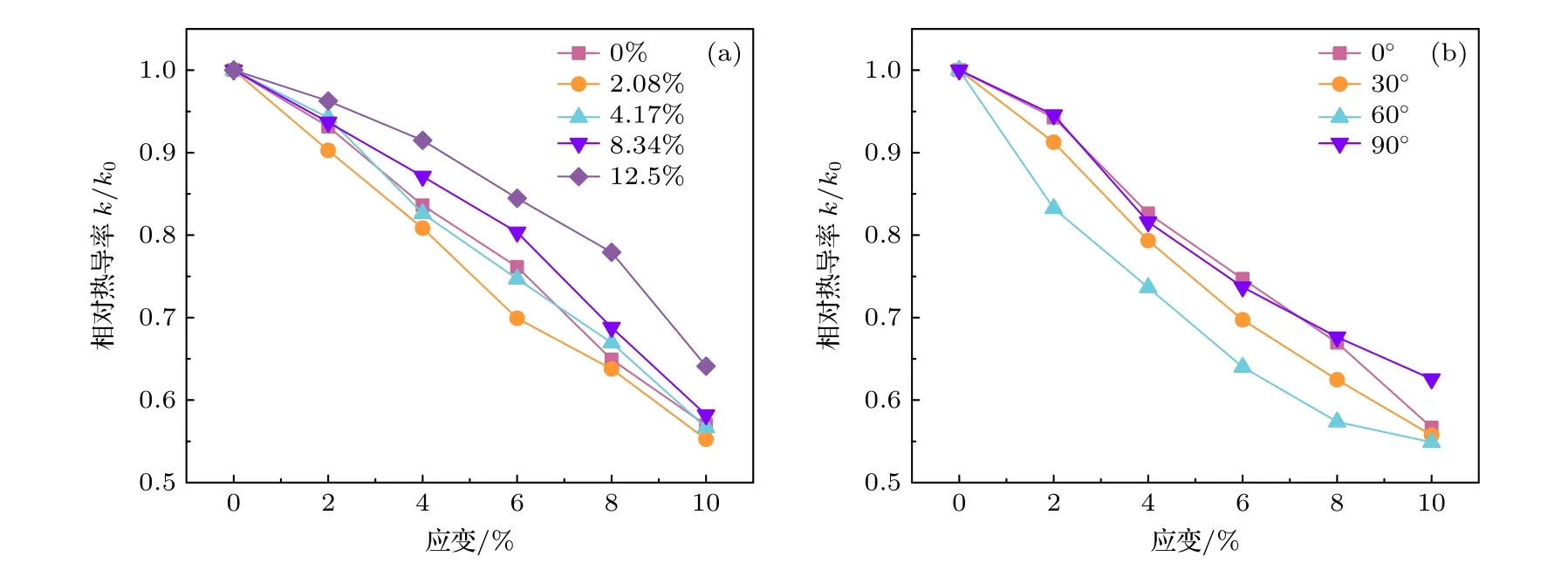
图8 (a) 不同的层间共价键浓度下应变对热导率的影响;(b) 不同层间共价键链角度下应变对热导率的影响Fig.8.(a) Influence of strain on thermal conductivity with different interlayer covalent bond concentrations;(b) influence of strain on thermal conductivity with different interlayer covalent bond chain angle.

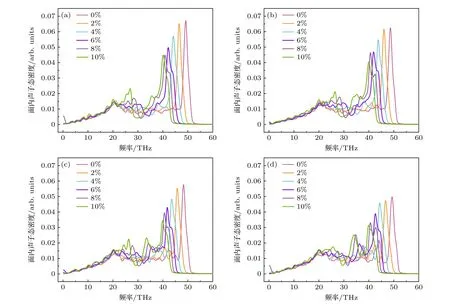
图9 不同拉伸应变下具有层间共价键的双层石墨烯的面内声子态密度 (a) 层间共价键浓度为2.08%;(b) 层间共价键浓度为4.16%;(c) 层间共价键浓度为8.33%;(d) 层间共价键浓度为12.5%Fig.9.In-plane PDOS of bilayer graphene with interlayer covalent bonds under different tensile strains: (a) Interlayer covalent bond concentration of 2.08%;(b) interlayer covalent bond concentration of 4.16%;(c) interlayer covalent bond concentration of 8.33%;(d) interlayer covalent bond concentration 12.5% interlayer covalent bond concentration.

图8(b)为层间共价键浓度为4.16%时,层间共价键链呈不同角度时,双层石墨烯纳米带热导率随拉伸应变的变化曲线.结果表明,10%的拉伸应变均使得不同层间共价键分布的双层石墨热导率下降了40%以上,与其他组相比,层间共价键与热流方向垂直时,受拉伸应变时双层石墨的热导率下降幅度较小.结果表明,可以通过机械应变进一步的降低具有层间共价键的石墨烯纳米带的热导率.