苏州地区软土地层深基坑侧向土压力分布规律研究
2024-01-06张颖欣张佳莉周小淇贾鹏蛟
王 飞,张颖欣,张佳莉,周小淇,贾鹏蛟
(1.苏州轨道交通集团有限公司,江苏 苏州 215004;2.苏州大学 轨道交通学院,江苏 苏州 215137)
基坑工程是开发地下空间的重要手段,地连墙作为深基坑工程主要采用的支护结构,其侧向土压力分布形式及变形特征直接关系到基坑开挖过程的安全。为避免地连墙由于侧向土压力而出现大变形甚至整体失稳,深基坑施工过程中需要架设多道支撑,以达到优化地下连续墙侧向土压力分布形式的效果。针对不同工况下的基坑围护结构侧向土压力分布形式,国内外学者已经取得较多的研究成果。Terzaghi和Peck[1]采用1/2分担法将大量现场实测的支撑轴力数据换算成土压力值,并根据不同地质特点将土压力绘制成不同的经验分布图。日本土木学会将土层看作均质土体,根据不同的地质条件通过现场实测数据绘出不同的经验土压力分布图[2]。杨光华等[3-6]提出了增量法计算基坑施工过程中地连墙的土压力分布规律,该方法采用朗肯土压力理论计算支护结构上侧向主动土压力,结合变形协调方程以及剪力与弯矩平衡方程计算各道支撑反力;再由1/2分担法将支撑反力转化为分布压力。彭社琴等[7]以润扬长江大桥某特定深基坑工程为研究对象展开实测分析,得出了三种土压力分布及围护墙变形特征。
随着地下空间开发的深层次推进,深基坑工程逐渐成为我国地下空间工程的重点。深大基坑主要分布于我国经济发达的东南沿海地区,然而该地区软土分布广泛。软土由于其强度低、压缩性大、透水性小与受荷变形大等特点,大大提高了基坑施工难度[8];加之周围环境复杂,软土地区的深基坑工程事故频发。因此,研究软土地层地下连续墙侧向土压力分布规律对深基坑工程的设计与施工具有重大意义。本文以苏州地区软土地层地铁车站深基坑工程为依托,对软土地区深基坑施工过程中地连墙所受侧向土压力分布规律展开研究,提出侧向土压力计算方法,为相关工程的设计施工提供依据。
1 工程概况
苏州市轨道交通5号线西起太湖旅游度假区旅游集散中心,向东进入高新区南部的横塘,线路总体呈南西—北东走向,横跨苏州,经过低山丘陵区及冲积湖平原,区域85 m深度范围内主要分布黏土、粉质黏土、粉土和粉砂。
苏州市轨道交通5号线目前已开挖到底的车站有29个,车站对应的基坑均为长条形基坑,其中超深基坑(开挖深度超过20 m)有9个,最大开挖深度达29 m,车站基坑开挖的支护形式均采用“地连墙+内支撑”。其中长江路车站基坑深16.5 m,地下水位位于地表以下1.5 m处,共设置四道支撑。该基坑第一道支撑为混凝土支撑,位于标高1.9 m处;第二至第四道支撑为钢支撑,分别位于标高-2.8 m、-6.4 m、-9.6 m处。长江路车站围护结构剖面图如图1所示,该支护形式是苏州地区软土深基坑工程的常见支护形式,后续分析依托长江路车站基坑工程展开。
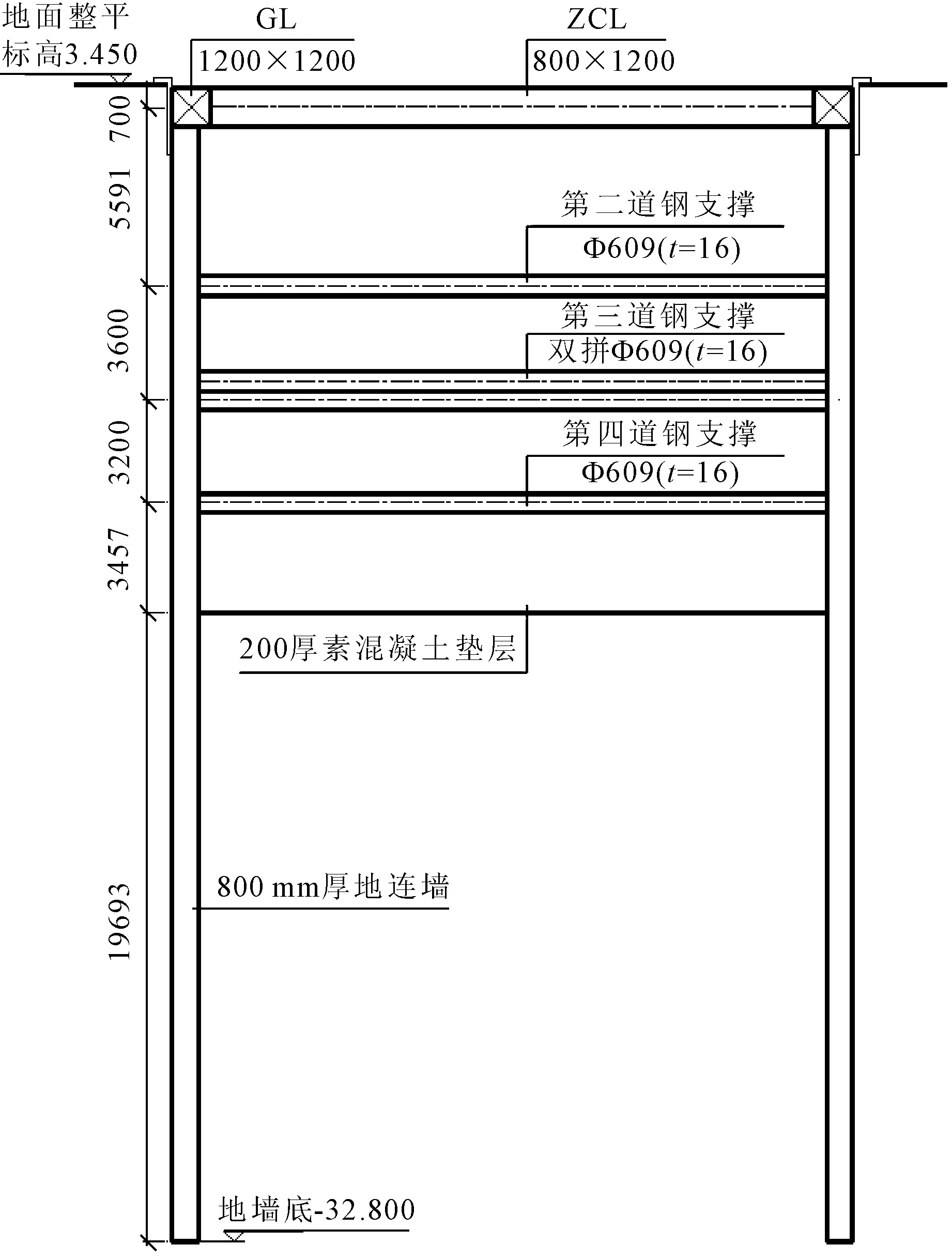
图1 长江路车站围护结构横剖面图
2 深基坑侧向土压力理论分析
2.1 增量法概述
深基坑施工过程中,土体的开挖卸载、支撑锚杆的架设均有时间效应影响,而增量法考虑开挖过程、支护体系刚度及围护墙体插入等,目前得到广泛认可,并被大量应用于工程实践[9]。增量法最先由杨光华[4]提出,常用于支护形式为“围护桩+内支撑”的基坑开挖计算[10],采用增量法计算时,作用在墙体上的土压力为上一次施工完成后到当前位置所产生的土压力增量。这部分土压力可以看作是由于被动区土体卸载产生的不平衡力[11]。
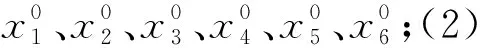
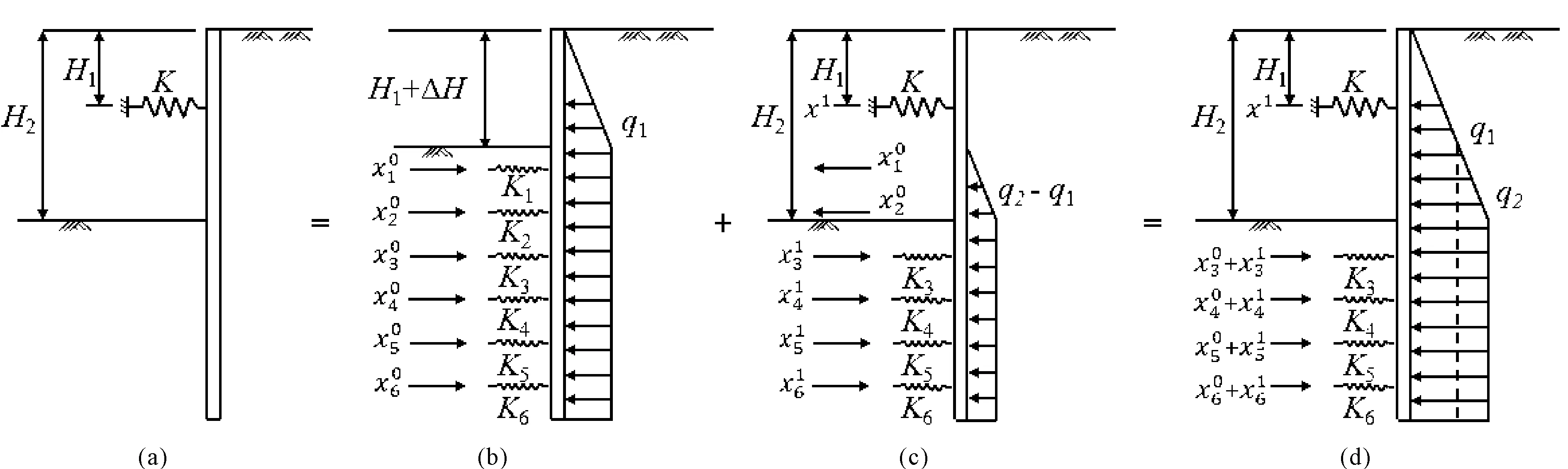
图2 增量法计算简图
2.2 深基坑侧向土压力增量模型推导
假设受压地连墙墙体单元的面积为b×d,b为墙单元的厚度,d为墙单元的宽度,其刚度系数K,由定义K=X/Δ,X表示相应弹簧集中力,q为单位面积分布压力,假设q=X/(b×d),Δ是由Boussinesq解求得的位移,位移表达式如式(1)。可进一步得弹簧刚度系数的表达式为式(2),但受边界条件影响,靠近地表附近弹簧的刚度系数应乘以2/3。
(1)
(2)
式中:Es为变形模量;vs为泊松比;ω为形状系数,特殊地,当b/d=1时,ω=0.88,当b/d=1.5时,ω=1.08,当b/d=2时,ω=1.22。
假定墙底端为完全固定约束,L表示地连墙嵌固深度,Xn表示土弹簧对墙的作用力,Yi表示土弹簧给墙体反力Xi的作用点到地面距离,利用力法与位移法求出土弹簧反力Xn,如图3(a)、3(b)所示。其中,H表示地连墙嵌入位置的水平荷载,M表示地连墙嵌固端由于H形成的弯矩。考虑到实际施工过程中地连墙的整体变形控制严格,建模过程忽略了地连墙及墙后土体的变形特征,两者在模型中的假定单元满足变形协调。
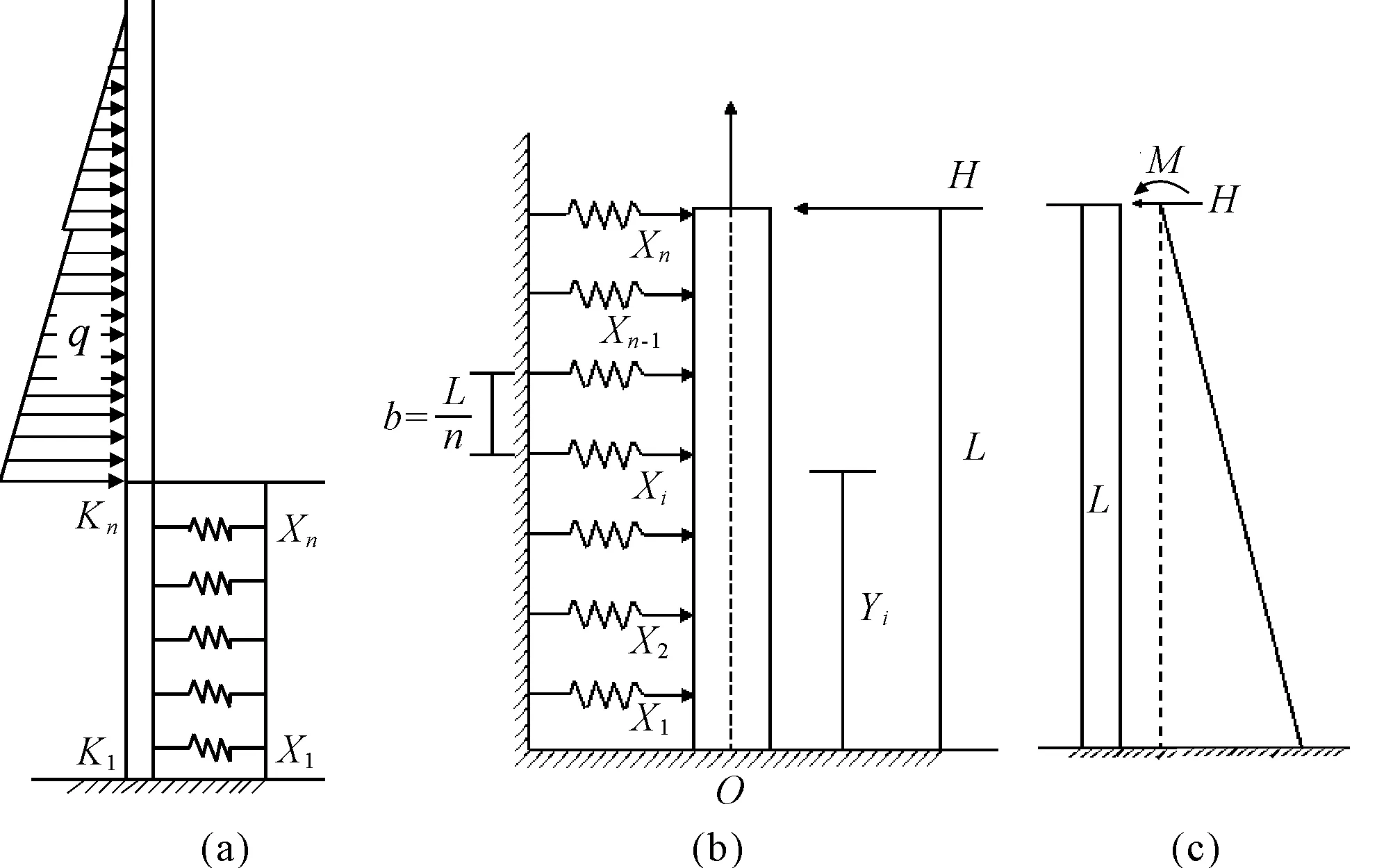
图3 改进增量法计算简图
在土弹簧与墙体接触处列出变形协调方程,如式(3)所示;此时墙体底部固定约束处的剪力与弯矩均为零,再列出两者的平衡方程,如式(8)及式(9)所示,联立各方程可求解,即得到各支撑以及土弹簧的未知反力,如式(10)所示。具体求解过程如下:
(3)
δij=Wij+Sij
(4)
(5)
(6)
(7)
式中:δij是柔度系数,表示在单位外力作用下Kj处的墙体位移;Xi为土弹簧对墙的作用力;Yi为土弹簧给墙反力作用点到地面距离;Δ0表示墙体底部处转角;φ为土体内摩擦角;Δip表示在外力H、M作用下Kj处墙体位移,如图3(c)所示;Wij为围护结构刚度系数;Sij为弹簧刚度系数;E为围护结构的弹性模量;I为围护结构的贯性矩;Ki为弹簧刚度;a=Yi/L。显然,方程组(3)中存在n个方程求解n+2个未知数的问题,因此在墙体底部根据剪力FX与弯矩M0为0的条件补充两个方程,如式(8)和式(9)所示。
∑FX=0[1 1 … 1 0 0]{X}=H
(8)
∑M0=0[Y1Y2…Yn0 0]{X}=M0
(9)
式中:X表示X1、X2…Xn、Δ0、tgφ的原始矩阵。
式(3)、式(8)和式(9)联立可写为:
(10)
式中:S表示式(3)中δn…-Yn的原始矩阵;T表示式(8)中1…0的原始矩阵;Y表示式(9)中Y1…0的原始矩阵;-Δp表示式(13)中-Δ1p…-Δnp的原始矩阵。
最终由式(10)解出未知反力X1、X2…Xn,任一截面处的弯矩M可由截面法求得。
2.3 模型可行性分析
为分析本文理论模型的可行性,本节将依托苏州市轨道交通5号线长江路车站基坑工程,用增量法计算得出的结果与上述两种理论进行对比分析。长江路车站基坑围护结构设计及地质情况如图4所示,其开挖和架设支撑顺序如表1所示。

图4 长江路车站基坑实例计算剖面图
支撑刚度分别为:K1=280520 kN/m,K2=186070 kN/m,K3=186070 kN/m,K4=186070 kN/m。
计算简图如图5所示。取单位长度墙体进行理论求解,每米墙体抗弯刚度为EI=3.3×107kN·m2。根据图5(a),计算得出不考虑施工过程的情况下墙体的支撑反力以及弯矩,如图6(a)所示;根据图5(b)—图5(f),用增量法计算得出考虑施工过程的墙体支撑反力以及墙体的弯矩结果,如图6(b)所示。

图5 计算简图
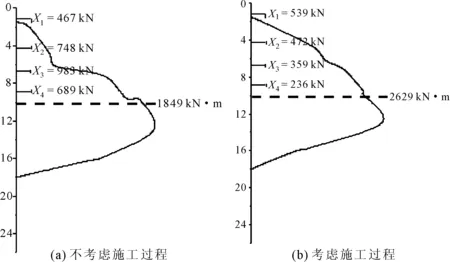
图6 增量法弯矩及支撑反力
对比图6中(a)和图6(b)可知:在墙体弯矩方面,当考虑施工过程对围护结构内力影响时,墙体的弯矩较大。因此,若将图6(a)计算所得的墙体内力用于基坑设计时的参考值,基坑结构设计将缺乏安全性,与文献[6]所述一致;采用增量法计算得到的支撑反力偏小,这主要是由于支撑架设时间不同,承担的增量荷载不同。以开挖最后一层土体为例,在架设支撑K4后,该支撑仅仅承担-10.1 m开挖至-13.1 m期间的500 kN左右的荷载增量,并且开挖面下的土体弹簧和上部分早先架设的支撑K1、K2、K3也分担该荷载,因此最后一道支撑的反力应如图6(b)所表示的236 kN,而不是图6(a)中K4的反力689 kN。
Terzaghi、Peck[1]采用1/2分担法,将收集到的芝加哥及柏林等地区地下铁道基坑工程中支护结构上各支撑轴力转化为土压力,得到不同地质条件下的经验土压力分布模式,如图7。
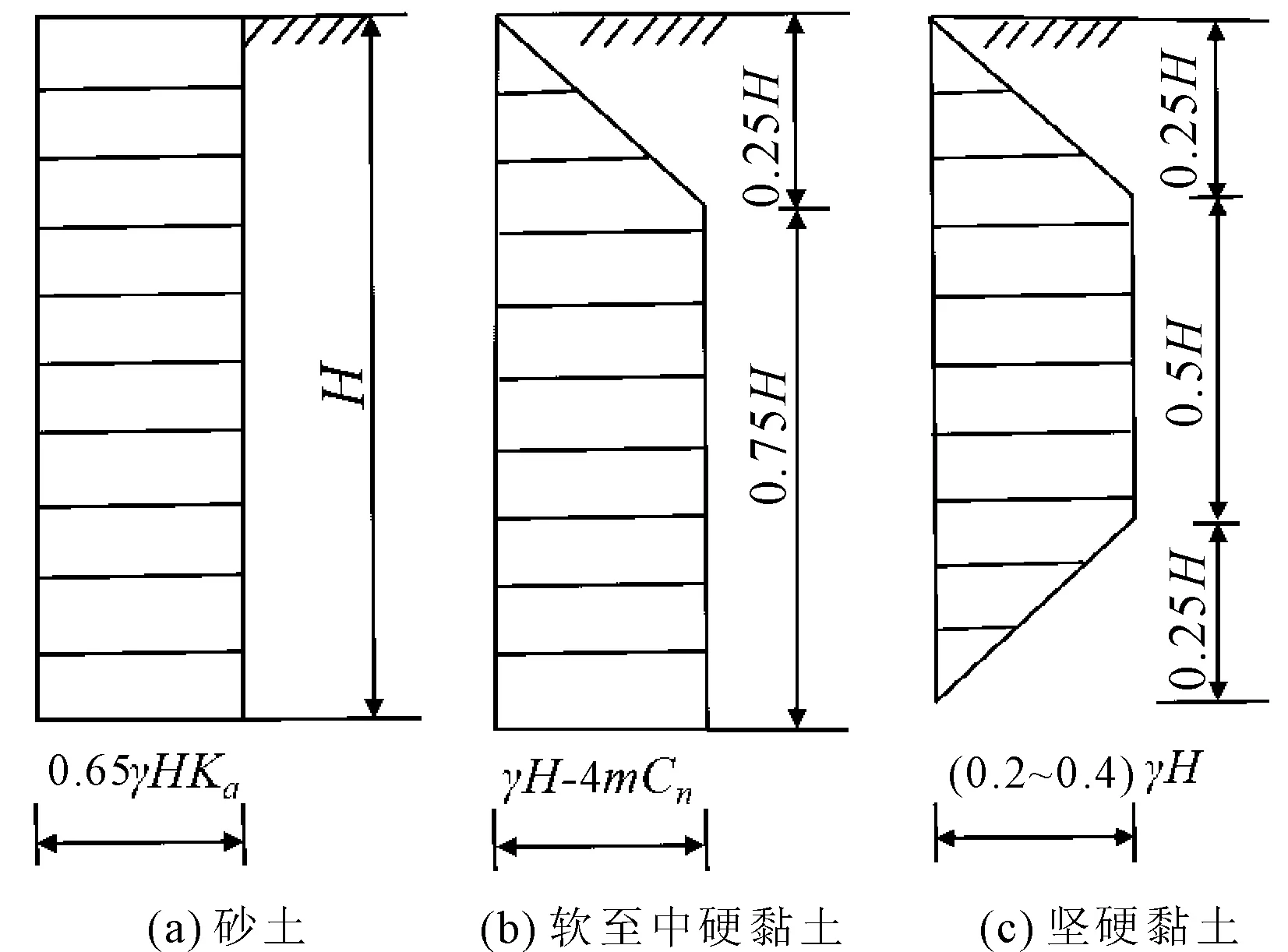
图7 Terzaghi-Peck经验土压力分布模式[1]
日本土木学会通过现场实测数据,绘制出不同地质条件下的经验土压力分布模式,如图8。为便于研究,在绘制分布模式图时将图层看作均质土体。
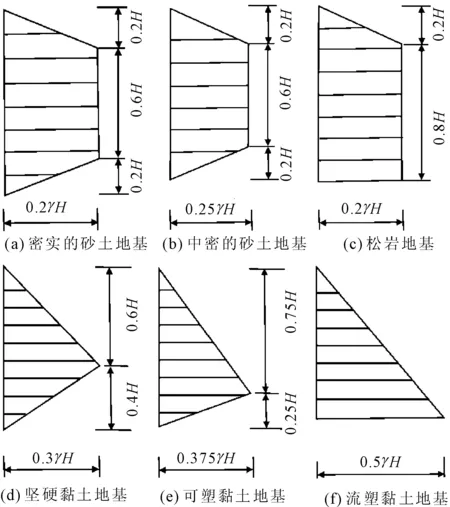
图8 日本规范采用的土压力分布图
为分析研究表观土压力与经典土压力理论间的关系,将增量法计算所得的开挖至底时各层支撑反力按照支撑上、下二分之一的间距范围转化为均布力(称为支撑分布力),并将其与朗肯土压力、T-P表观土压力及日本土木学会提出的经验土压力计算结果进行比较,如图9所示。

图9 增量法计算的土压力值与各土压力比较
如图9所示,增量法计算的土压力分布处在Terzaghi和Peck所给出的表观土压力分布曲线内,且其分布趋势与日本土木学会给出的经验土压力分布模式吻合;与朗肯土压力分布模式相比,增量法计算的土压力在上部分支撑中较大,在下部分支撑中较小,这是由于增量方法考虑了施工过程:上部分支撑设置早于下部分支撑,先承担土体卸载后的荷载,导致上部分支撑分布力较大;而下部分支撑发挥作用较晚,部分荷载已经被上部支撑承担,导致下部分支撑力较小,与文献[6]描述相契合,且更加合理[12]。因此支撑分布力以及经验土压力分布图式并非与真实土压力分布一致,作用于基坑围护结构上的土压力仍然符合是经典土压力理论计算土压力(即图9中呈三角形分布的土压力)。由图9可知,本文所求的支撑力分布趋势与经验土压力的分布相吻合,表明理论模型的可行性,后续将进行数值分析以进一步研究土压力的分布形态。
3 深基坑开挖施工数值分析
3.1 模型概况分析
考虑到基坑开挖卸荷过程中土体应力路径的变化,模拟选取硬化土(HS)本构模型。HS模型共有11个非线性参数,其中关键参数有:固结试验中的参考切线模量Eoedref、三轴排水剪切试验中的参考切线模量E50ref、三轴排水剪切试验中的参考加卸载模量Eurref。据现有研究成果,上述3个关键参数取值均有一定范围[13-15],例如:Eoedref=(0.8 ~ 1.1)Es0.1-0.2;对于黏土,E50ref=(1 ~ 2)Eoedref,Eurref=(3 ~ 6)E50ref;其中Es0.1-0.2为100 kPa~200 kPa压力段的土体侧限压缩模量。综合考虑,本文取E50ref=Eoedref=Es0.1-0.2,Eurref=3E50ref。
依托长江路车站基坑工程,使用PLAXIS 2D软件对该基坑开挖情况进行建模分析。基坑为降水开挖施工,地下水位在地表下1.5 m处,模拟过程需要考虑地下水渗流。基坑开挖深度和宽度分别取16.5 m和20 m,模型尺寸为200 m×80 m,包括5 050个单元,41 207个节点。模型底端设置为完全固定约束;两侧边界为水平约束(ux= 0;uy自由);地下水渗流边界条件为:模型两侧边界的地下水头保持78.5 m,关闭模型底部边界(不透水),模拟过程中设置地下水稳态渗流,如图10所示。HS模型的土层材料参数取值如表2所示、结构单元的参数设置如表3所示。

表2 土层材料参数表

表3 结构单元材料属性参数表(单位长度墙体)
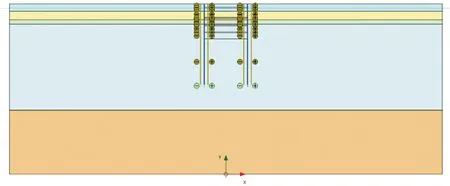
图10 基坑计算模型
3.2 模拟步序
基坑开挖过程的模拟步序的如表4所示。
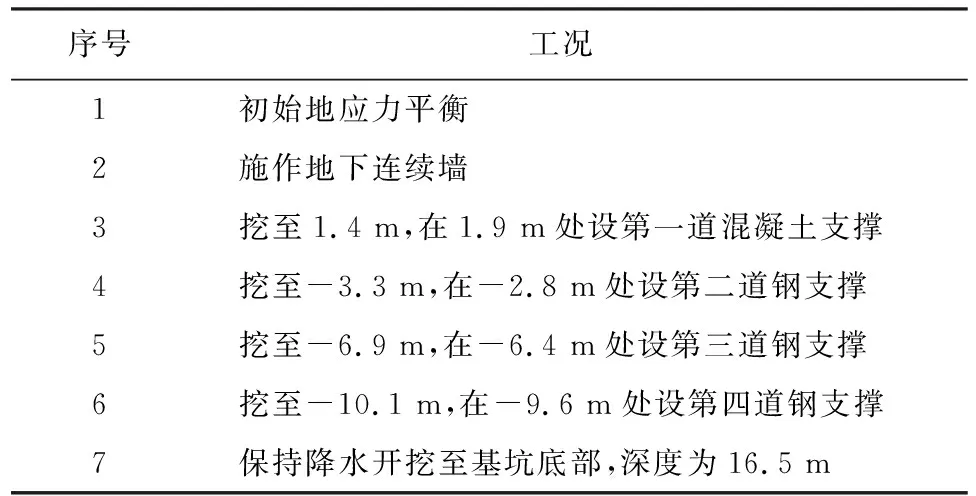
表4 模拟步序
3.3 模拟结果对比分析
将数值模拟结果的变形数据与实测数据进行对比,如图11、图12所示。地表沉降模拟值与实测值接近、地连墙的模拟侧移值与实测侧移值接近,且变化趋势吻合,表明模型参数选取及建立过程都较为合理;由该模型得到的数值模拟结果具有准确性,能够真实地反应苏州地区基坑支护结构的变形规律,为苏州软土地区基坑设计及施工提供参考。
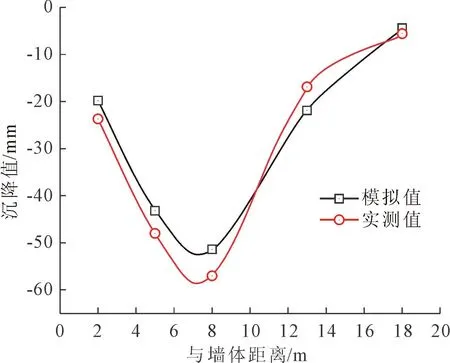
图11 地表沉降模拟与实测对比

图12 地连墙模拟与实测对比
图13展示了各模拟工况下地连墙水平位移变化趋势。由图13可知,在架设第一道混凝土支撑后,地连墙最大侧移量约为1.8 mm,发生在墙顶处;继续开挖至6.8 m并架设第二道钢支撑后,地连墙埋深8.7 m处发生最大位移,地连墙侧移量增至6.2 mm;继续开挖至10.3 m并架设第三道钢支撑后,地连墙埋深12.3 m处发生最大位移,地连墙侧移量增至13 mm;再继续开挖至13.7 m并架设第四道钢支撑后,地连墙埋深15.9 m处发生最大位移,地连墙侧移量增至34 mm。由上述分析可知,地连墙最大侧移均发生在开挖面以下2.0 m处左右。
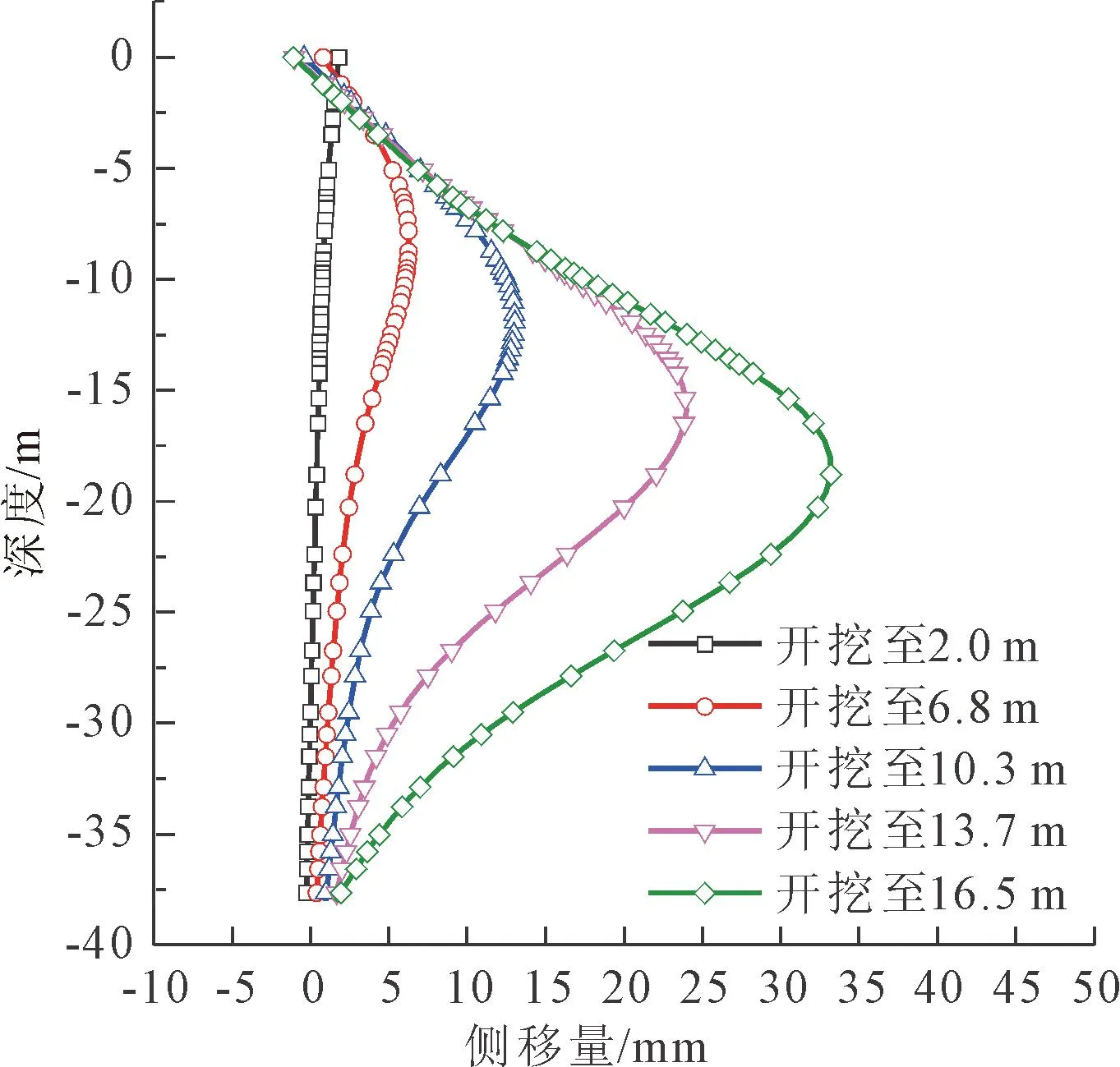
图13 地连墙侧移曲线
3.4 土压力分布模式分析
为更好研究苏州地区深基坑围护结构土压力分布模式,整理了苏州市轨道交通5号线29个基坑的实测数据,与长江路车站基坑类似,其他部分基坑也为首道混凝土支撑。由于混凝土干缩湿胀,混凝土支撑轴力会偏大;不考虑首道混凝土支撑的轴力,根据增量法的计算结果对第四道、第六道混凝土支撑的轴力进行修正。
基坑的轴力实测数据如图14所示。
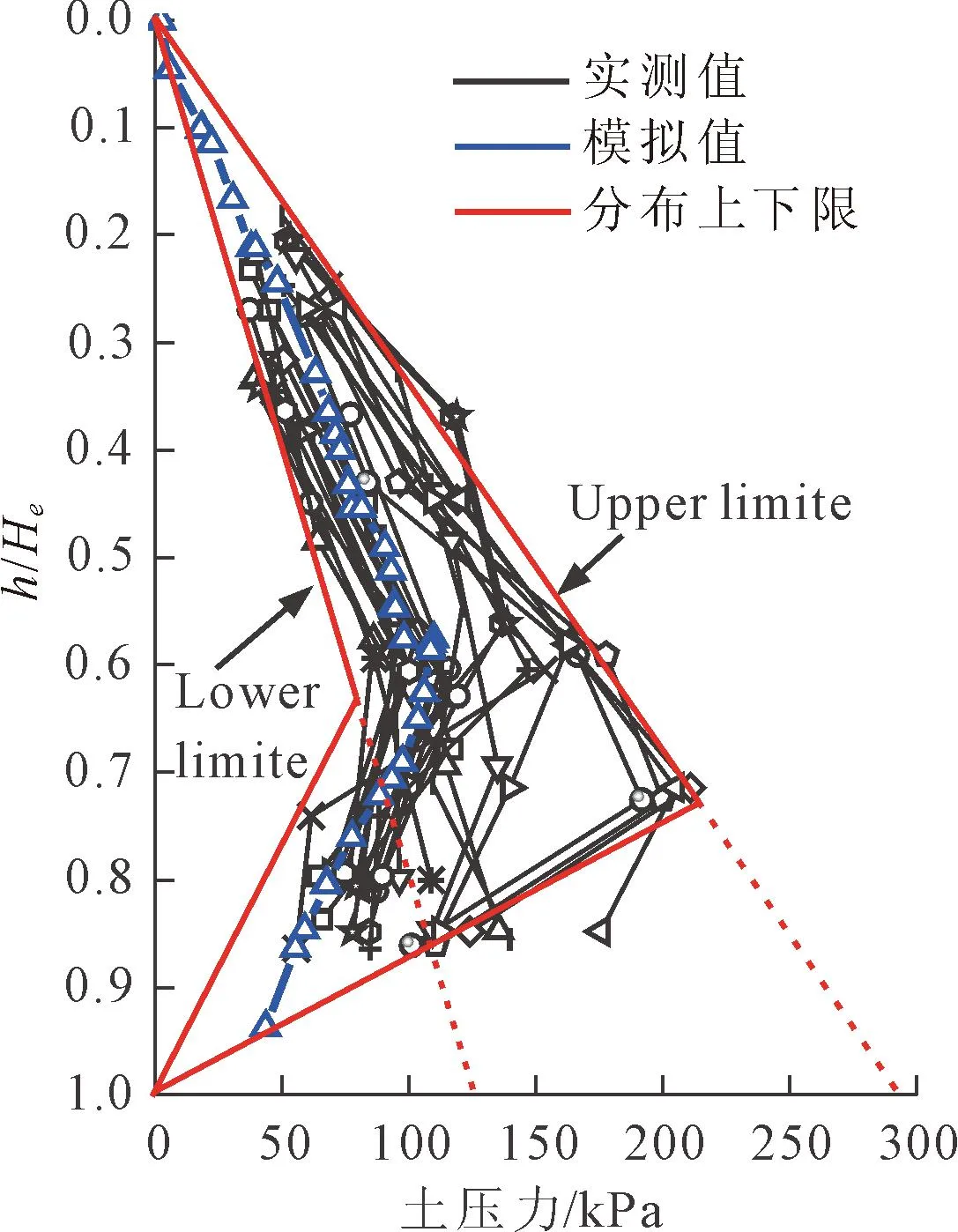
图14 支撑分布力
由图14可知,最后一支撑的分布力都较小。由于最后一道支撑架设时间晚,大部分载荷已由先架设的支撑承担。假设土体是重度为19 kN/m3的均质土,可以计算土压力分布的上、下限,确定侧向土压力K的取值范围为0.3~0.7。将2.3节模拟计算的土压力分布值与实测值对比分析,最终总结出适用于苏州地区的经验土压力分布模式,如图15所示。

图15 苏州地区经验土压力分布模式图
4 结 论
本文依托苏州市轨道交通5号线长江路车站基坑工程,利用增量法模型对软土地层地下连续墙的侧向土压力展开了理论分析,并利用数值模拟研究了基坑开挖过程中侧向土压力的分布规律,得到的结论如下:
(1) 施工过程对地连墙墙体的弯矩影响较大;为保证基坑围护结构设计的安全性,需要将施工过程的影响纳入地连墙设计。
(2) 对比增量法、表观土压力和经典土压力等理论计算所得结果可知,支撑分布力以及经验土压力分布图并非真正的土压力,真实作用于基坑围护结构上的土压力仍然呈三角形分布。
(3) 利用1/2分担法分析苏州地区软土支撑分布力形态,得到土压力的分布上下限值,并得出侧向土压力系数K建议取值范围为0.3~0.7。
(4) 对比分析土压力理论计算、工程实测及数值模拟结果,得出了适用于苏州地区软土的经验土压力分布模式。
