海港纳潮量预测有限元分析

2024-01-06栾明珠杨佳欢

天津建设科技 2023年6期

栾明珠，杨佳欢

（烟台仲伯企业管理咨询有限公司，山东烟台，264000）

我国海岸线长，海岸线的生态环境极易受人类活动的影响。在沿海工程建设活动中，人类对地表土壤进行开挖、填埋，对地表水和地下水进行抽排、疏通等，均会对区域生态、地貌和水文等造成扰动；由于海洋水环境与陆地地下水盐分、矿化度的不同，一些海港疏通完成后，潟湖水系不可避免受涨潮落潮影响，区域水文生态环境发生变化。为了分析潟湖水系受潮汐的影响程度，研究潟湖水量的潮流场变化规律，预测海港的纳潮量显得尤为重要。

国内外学者针对海港纳潮量的预测展开了相关研究，王璐等[1]基于MIKE21 水动力数值模型，对芝罘湾围填海工程引起的4个特征年潮流场和纳潮量进行了分析，指出地形对潮流流速具有明显影响；李希彬等[2]利用FVCOM 海洋数值模型预测未来海岸工程建设后天津近海的水动力和水交换的变化，指出工程建设会延长水体半交换周期约10 d；陈志琦等[3]基于MIKE21 水动力数值模型，分析了罗源湾海域的Smagorinsky 系数、糙率和风拖拽系数，研究了涨落潮时湾域内的纳潮量及潮汐流速。现有研究均集中在涨潮和落潮的海域纳潮量、水动力和水体流速变化，考虑大潮和小潮工况的纳潮量预测较少，同时针对水系疏通引起纳潮量变化和水域水动力和水体交换方面的研究鲜见报道。

荣成市地处山东半岛最东端，三面环海。荣成市某地潟湖水系疏通工程面积约288.36万m2，总水系疏通土方约219.81 万m3，本文以该工程为背景，搭建生态修复工程的水动力数学模型，通过模型分别模拟大小潮两个时期不同方案潟湖工程前后所容纳的整体水量，分析潟湖进行水系疏通工程前后纳潮量等参数的变化情况，对生态修复工程实施导致的特征值变化给出量化数值，为该区域生态修复工程提供技术支撑并提出相关的合理建议。

1 潮流水动力数学模型及工程海域有限元模型建立

1.1 潮流水动力数学模型

采用平面二维数值模型模拟工程海域的潮流场。该模型采用非结构三角网格剖分计算域，能较好地拟合陆边界，设计灵活且可随意控制网格疏密。潮流水动力的控制方程[3～4]

式中：t为时间；x、y为笛卡尔坐标系空间坐标；η为水面高程；d为水深；h为总水深，h=η+d；u、v为流速在x、y方向上的分量；f为科氏力；g为重力加速度；ρ为水体密度；ρ0为参考密度；pa为大气压强；sxx、sxy、syx、syy为辐射应力分量；Txx、Txy、Tyx、Tyy为水平黏滞应力；（τsx，τsy）和（τbx，τby）为水面和底床的切应力在x、y方向上的分量；S为源汇项流量；us、vs为源汇项对应的速度分量。

在二维浅水方程中流速是一个平均的概念，应满足

表面风应力可以表示为[5]

式中：ρa为大气密度；cd为风的拖曳力系数vw)为海面以上10 m处的风速。

与表面应力有关的摩阻流速为[6]

潮流模型底部应力的计算一般采用二次形式，将底部应力看作是速度的函数。底部切应力根据牛顿摩擦定律其可定义为

式中：cf为拖曳力系数=(ub,vb)为底层流速。

与底部切应力有关的摩阻流速为

式中：C为谢才系数；M为曼宁系数，可以通过底部粗糙度ks估算，M=25.4ks-0.1667。

1.2 工程海域有限元模型建立

海域数学模型采用大小模型嵌套的方式：大模型计算选取周边海域100 km×88 km，小模型计算选择某地潟湖及外海至鸡鸣岛部分海域。模型计算最小时间步长0.5 s 以保证运行稳定。模拟采用非结构三角网格，工程建设前整个模拟区域内由9 403 个节点和15 080 个三角单元组成；最小网格间距10 m。为了更好地对比工程建设前后的潮流场变化，海域网格保持一致。见图1。

图1 大模型计算域网格

为了解工程附近海域的潮流状况，对网格进行小范围嵌套处理，小范围的工程总平面方案共4 种：方案一工程底标高为-0.5 m，为满足船舶吃水条件，对沟槽处进行水系疏通，沟槽处设计底标高-1.0 m、宽度200 m，其他区域设计底标高-0.5 m，边坡比为1∶5；方案二水系疏通范围为潟湖西侧现有全部水域区域，总疏通面积约340万m2，设计底标高-2.5 m，边坡比为1∶5；方案三水系疏通范围为潟湖西侧现有全部水域区域，总疏通面积约340 万m2，设计底标高-1.5 m，边坡比为1∶5；方案四水系疏通范围为潟湖西侧现有全部水域区域，总疏通面积约340 万m2，设计底标高-1.0 m，边坡比为1∶5。见图2。

2 仿真计算结果分析

分别模拟大潮和小潮时段整个潟湖区域工程前后所容纳的整体水量；潟湖内高潮时总水量与低潮时总水量差即为纳潮量。工程区所在海域潮位具有明显的半日潮特性，属于不规则半日潮类型，每天出现两次高潮和两次低潮且峰值均不相同，本次预测分析选择大潮和小潮两个典型潮期。见图3。

2.1 方案一

大潮期间一个周期内最大潮差1.0 m 左右，两次高潮的潮差相差0.6 m 左右；高潮期间最大纳潮量为3.65×106m3，低潮期间纳潮量为1.13×106m3。小潮期间一个周期内最大潮差0.7 m 左右，两次高潮的潮差相差0.2 m 左右；高潮期间最大纳潮量为2.15×106m3，低潮期间纳潮量为9.32×105m³。见图4和表1。

图4 方案一大小潮期间潟湖潮位过程曲线

2.2 方案二

大潮期间一个周期内最大潮差1 m 左右，两次高潮的潮差相差0.6 m 左右；高潮期间最大纳潮量为3.67×106m3，低潮期间纳潮量为1.15×106m3。小潮期间一个周期内最大潮差0.7 m 左右，两次高潮的潮差相差0.2 m 左右；高潮期间最大纳潮量为2.17×106m3，低潮期间纳潮量为9.41×105m3。见图5和表2。

表2 方案二施工后大小潮纳潮量

图5 方案二大小潮期间潟湖内潮位过程曲线

2.3 方案三

大潮期间一个周期内最大潮差0.8 m 左右，两次高潮的潮差相差0.5 m 左右；高潮期间最大纳潮量为3.76×106m3，低潮期间纳潮量为1.17×106m3。小潮期间一个周期内最大潮差0.6 m 左右，两次高潮的潮差相差0.3 m 左右；高潮期间最大纳潮量为2.24×106m3，低潮期间纳潮量为9.74×105m3。见图6和表3。

表3 方案三施工后大小潮纳潮量

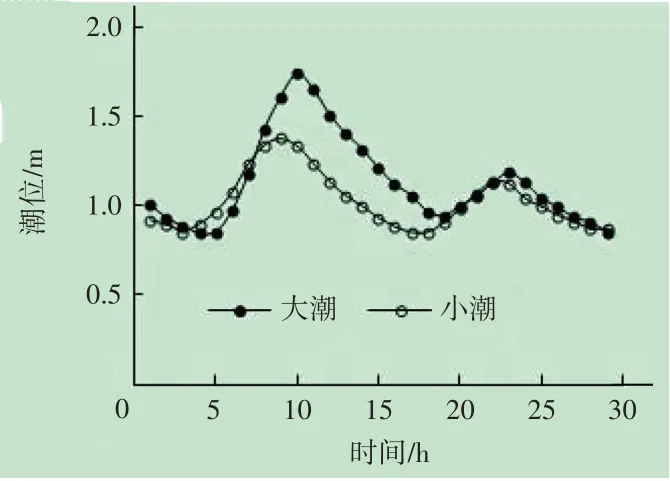
图6 方案三大小潮期间潟湖内潮位过程曲线

2.4 方案四

大潮期间一个周期内最大潮差0.8 m 左右，两次高潮的潮差相差0.5 m 左右；高潮期间最大纳潮量为3.66×106m³，低潮期间纳潮量为1.15×106m3。小潮期间一个周期内最大潮差0.6 m 左右，两次高潮的潮差相差0.25 m 左右；高潮期间最大纳潮量为2.16×106m3，低潮期间纳潮量为9.36×105m3。见图7和表4。