基于示波器的陀螺进动实验设计

王 悦,孙子尧,王 波,王新义,刘 洋,王亚平

(铜陵学院 电气工程学院,安徽 铜陵 244000)

引言

进动现象应用十分广泛,如陀螺仪、中国自主研发的单框架力矩陀螺、地球产生的岁差、自行车的拐弯等科技上和生活中常见现象都与进动相关[1-5]。从广义上说刚体能绕某一轴持续转动,同时此轴又绕另一交汇轴转动的运动就称为刚体的进动(precession)。工程上经常将绕着固定点高速自转(rotation)的对称刚体称为陀螺。玩具陀螺高速自转时,可以看成对称刚体绕定点运动,会出现如图1和图2所示的进动现象。陀螺进动的研究多数是单独计算自转和进动[6-8],而自传和进动往往都是同时进行的,此类方式得到的结果误差较大。少量设计涉及到自转角速度和进动角速度关系的探讨以及验证,如文献[9]。

图1 进动一

图2 进动二

文献[9]中利用激光器和光敏电阻设计实验探究了自转和进动角速度关系,但由于光敏电阻和激光器相互作用需要反应时间,因而有可能会增大误差。本文将实验进行优化,利用示波器,结合法拉第电磁感应定律以玩具陀螺为研究对象,探讨陀螺进动时的基本规律。

1 理论分析

1.1 进动一类型

从物理原理上对陀螺的进动现象产生原因做具体分析。图1中陀螺在直立高速旋转的过程中如果没有摩擦力,那么就会一直旋而不倒,因为陀螺竖直状态下重力和支持力的合力矩为零。但是由于现实中存在摩擦力,陀螺在直立旋转一段时间后就会因为受到重力而产生倾倒,一旦倾倒,陀螺自转的轴与竖直方向的轴就会产生一个夹角θ,如图3所示。重力力矩可以表示为:

(1)

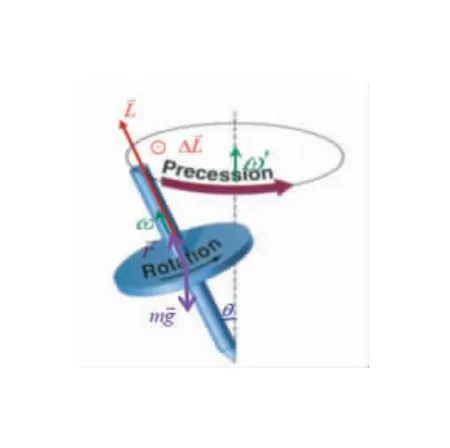
图3 进动力矩分析

图4中将角动量和角动量的变化投影到进动绕行的圆周上,可以得到几何关系

(2)

所以

(3)

图4 进动角动量分析

同时由定轴转动定律可知

(4)

所以

mgrsinθ=ω′Jωsinθ

(5)

因而

(6)

1.2 进动二类型

对图2的陀螺可以进行类似分析,如图5所示。当陀螺的轴绕着竖直方向的轴在旋转时,因为有重力力矩的存在就会有一个与角动量垂直的角动量变化,同样可以把角动量投影到进动运动的圆周上进行分析,可以得到与(5)式相同的结果,从而可以得到与(6)式类似的关系。此关系说明陀螺自转的角速度为ω,进动的角速度为ω′,满足乘积为一定值,此定值与陀螺的转动惯量J相关。

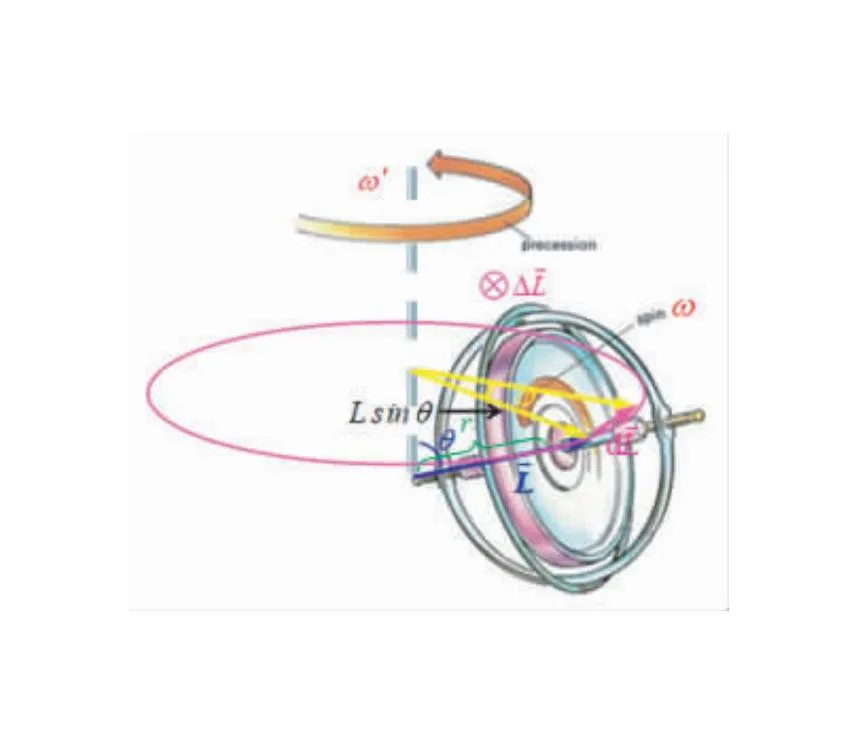
图5 进动理论分析

2 实验设计

2.1 实验测量

为验证理论分析的正确性设计如下实验装置,如图6所示。为了测出自转和进动角速度,在陀螺上对称贴上3个小磁片,如图7所示,当陀螺高速旋转并做进动时,3个磁片会随着陀螺一起旋转,就会产生周期性变化的磁场,当周期性变化的磁场经过螺线管上方,螺线管内部将产生周期性变化的感应电流,通过示波器可以实时地把电流的变化波形显示出来。

图6 实验装置

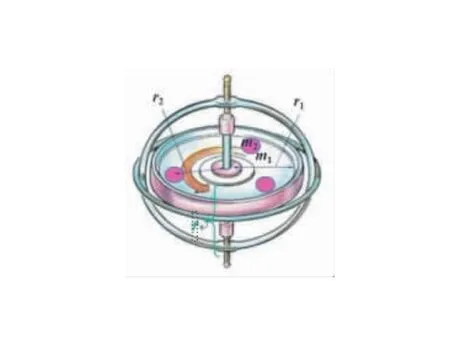
图7 安装磁片的陀螺

通过(6)式可以得出

(7)

在(7)式中m为陀螺质量m1与三个磁片3m2之和,r为陀螺质心到竖直绳的距离,实验中测得m1=44.7 g,3m2=1 g,r=3.6 cm,那么通过上述实验设计测得自转的角速度为ω,进动的角速度为ω′,代入(7)式就能算出陀螺的转动惯量实验值,实验测量数据列于表1中。

表1 实验测量陀螺自转周期、进动周期、角速度关系及转动惯量

图8是通过表1数据拟合出的自转角速度与进动角动量之间的数量关系,发现自转角速度与进动角动量满足反比例关系,所以两者乘积为一定值。这与前面理论分析相符合。

图8 自转角速度与进动角动量数量关系

2.2 误差分析

图7中r1为陀螺半径,r2为陀螺质心到磁片中心的距离,由平行轴定理可写出陀螺转动惯量的理论计算式:

(8)

实验中测得:r1=2.3 cm,r2=1.8 cm,代入(8)式可得

=1.241 2×10-5

(9)

表1中转动惯量的平均值为1.249 7×10-5kg·m2,由(9)式转动惯量的理论值1.241 2×10-5kg·m2,相对误差为

(10)

B类不确定度为

(11)

因此最终可以得到转动惯量值为

J=(1.2497±0.02)×10-5kg·m2

3 结果讨论

本文提出了一种利用法拉第电磁感应定律加上示波器测试陀螺进动的实验方案。首先,通过理论推导得出有摩擦力的情况下,陀螺进动时其进动角速度和自传角速度的一般规律。其次,通过设计实验对比了陀螺转动惯量的理论值和实验数值,两者的相对误差为0.68%,说明了理论分析的正确性和实验设计的合理性。本设计的物理原理与实验装置,可以应用到其他类似的刚体转动惯量测量实验中。