策略委托下古诺双寡头博弈的动力学行为

吴怡晓，褚衍东

（兰州交通大学 数理学院，甘肃 兰州 730070）

传统的双寡头博弈主要集中于静态均衡和纯策略，而静态均衡分析将会丧失大量有用信息。1978年，Rand最先研究了动态寡头博弈，使得寡头博弈随着非线性理论的不断发展及广泛应用，从静态分析上升为动态分析。Elsadany A A[1]引入一个具有外部效应的成本函数，基于相对利润最大化问题讨论了系统平衡点的稳定性，给出了系统通向混沌的两条路径。Peter H和Michael K[2]研究了在产品存在差异化的情况下，代理人在数量与价格之间选择价格竞争时，企业的利润以及消费者剩余会更高。Domenico D G 和Fabio L[3]研究了静态博弈中，等弹性需求及策略委托下，从长远来看，当两家企业提供混合激励合同时，企业将实现福利最大化。钟德强和仲伟俊[4]采用二阶段的博弈模型，研究了异质产品的Bertrand 竞争中，委托代理将会使企业间的竞争程度减小，增加企业利润，同时会使得企业的兼并动力增强，且产品的差异化程度越大，兼并企业采取的激励机制会越有效。唐要家和唐春晖[5]运用两期静态博弈模型，证明了企业策略对经营者的激励作用十分重要，且当今企业制度的演化是市场竞争策略和企业内部激励效应间相互权衡的结果。

利润最大化是企业发展过程中追求的目标，在相同的行业间，企业在追求自身利益最大化的同时更希望能比竞争者获得更多的利润，即实现相对利润最大化。因这种情况更加符合现实，因此，更多的学者将这一因素加入研究的对象中。Satoh A 和Tanaka Y[6]研究了Bertrand 竞争下，基于凸成本函数及同质商品的绝对与相对利润加权和的最大化问题，研究表明相对利润的权重与均衡价格的区间成反比。Li H 等[7]通过建立有研发溢出效应的动态模型，研究研发溢出参数对于企业的利润与相对利润的影响，给出系统通向混沌的两条路径，以及利用吸引盆分析了系统的多稳态行为。Huang Y M[8]等基于相对利润最大化建立混合双寡头博弈模型，以调整速度和产品差异化程度为对象，分析系统的复杂性和全局性质。

动态博弈模型中，系统随时间推移的过程中会产生非常复杂的动力学现象，因此一些学者利用分岔、分形以及混沌等非线性动力学的理论来解释经济系统的复杂性。Bischi G I[9]在研究中发现吸引盆具有相当复杂的结构，同时，证明了多稳态行为即吸引子共存，这种现象的产生与博弈之始的历史选择有关，即路径依赖。Liu Y X 等[10]建立了等弹性需求和委托代理下的Cournot双寡头博弈模型，研究了弹性系数对于系统的影响，并讨论在其他参数的影响下，系统的两种全局分岔行为。Zhu Y L等[11]建立了Cournot-Bertrand 混合博弈模型，主要利用二维分岔图对稳定区和稳定性条件进行分析，并讨论吸引盆的拓扑结构以及吸引盆中洞的形成原因。Elsadany A A[12]建立了异质商品下的Kopel 博弈模型，对其中的复杂动力学行为进行了研究，并对系统施加了控制以延迟混沌现象的产生。

虽然大量研究者将Couront博弈模型进行变形，但现有文献中基于策略委托的模型中大多是静态的，且只对静态模型的Nash 均衡点进行理论分析，因此其中产生的丰富动力学现象将会因为静态博弈模型而被掩盖。因此本文基于策略委托和相对利润，建立动态Cournot 博弈模型，用数值模拟的方法结合非线性动力学理论，来研究模型中的不同参数对系统动力学行为的影响。

1 模型建立

假设两家企业分别为企业1 和企业2。qi(i=1,2)表示第i家公司的产量。考虑一个有预算约束的消费者效用函数

消费者预算约束条件为

其中a表示市场需求规模，c为边际成本，本文考虑两家企业具有相同的边际成本。b表示两家公司所生产产品的差异化程度，b∈[0,1]，b越趋近1，则产品的差异化程度越小，b越趋近0，则产品的差异化程度越大。M表示消费者在该产品上的预算。通过求解具有约束条件的极大值问题，可得两家企业的逆需求函数为

考虑一个反映外部性的相互依赖的成本函数[1]

其中di(i=1,2) 是反映外部性的一个参数。为更好地解释di的意义，令bi=b+di(i=1,2)[1]，bi亦代表产品的差异化程度，其中bi∈[0,1]，bi∈(0,1) 时，两家企业生产的产品是不完美的替代品，而当bi=1 时，两家企业生产的产品完全可以互相替代。如果bi=0，那么q1和q2往往是独立的，在这种情况下，每个参与者都表现为垄断者。

由以上假设可知企业i的利润为

为提高公司的运行效率，本文考虑两家企业均雇佣专业的代理人来管理公司，且企业主均与各自的代理人签订一份利润与收入的激励合同，以此来要求代理人在公司利润与自身利润之间做出权衡。则在此合同下，代理人i的目标函数为

其中αi表示企业i目标函数的利润权重系数，且满足αi∈[0,1] 。αi越趋近1，表示企业的代理人越将公司的利润最大化作为目标，相反，越趋近0，表示代理人越追求自身利益最大化。除此之外，在实际市场环境中，追求相对利润最大化比追求自身的绝对利润最大化更加符合人性[1]，因为两家寡头中的任何一方都希望自己在竞争过程中完胜对方。从而，每家企业代理人的相对利润Mi(i=1,2) 可以看成是其自身的目标函数mi(i=1,2) 与其竞争对手的目标函数mj(i=1,2)且i≠j之差。因此企业代理人i的相对利润Mi的表达式为

则企业代理人i的边际相对利润为

由于竞争过程中参与者不会将信息完全公之于众，因此竞争对手不可能完全知晓市场及其他竞争者的信息，因此假设两家企业的管理者都是有限理性的，即管理者会根据t时期的边际目标来调整t+1 时期的产量，即，企业i在t+1 时期的产量增加；，企业i在t+1 时期的产量减小。则

其中vi表示企业i对其产量的调整速度（vi＞0）。

将式（8）带入式（9）可得二维动态博弈模型式（10）。

2 均衡点的局部稳定性分析

为简化计算，令

在模型（10）中，令qi(t+1)=qi(t)，求得模型的四个均衡点分别为

当A1＞0，A2＞0，2A1-A2B＞0，2A2+A1B＞0 时，上述均衡点才有意义。

E1是系统的平凡均衡点，这意味着两家企业都破产并退出市场；E2、E3是系统的边界均衡点，边界均衡点意味着一方企业破产，另一方成为市场上唯一的寡头垄断者，即整个市场被一家企业垄断。两家企业在达到Nash均衡状态时，并不意味着此后的市场状态将平静如水，因为Nash均衡点只是局部稳定的，因此均衡态是短暂的，如果任何一家企业做出微小的策略调整，Nash 均衡点的稳定性将发生改变，系统可能随之产生复杂的动力学现象。因为，因此E4为系统唯一的Nash 均衡点。

系统在任意一点()q1,q2处的Jacobian矩阵为

命题1E1是一个不稳定的结点。

证明：将E1带入式（12），得到系统Jacobian矩阵

很明显，矩阵J(E1)是一个对角矩阵，对应的特征值由对角项给出，λ1=1+v1A1，λ2=1+v2A2，由调节速度v1、v2和辅助变量A1、A2的非负性可知，λ1＞1，λ2＞1。因此，E1是一个不稳定的结点。

显然λ2＜1。

命题3（1）当0 ＜A1v1＜2 时，E3是一个鞍点。

（2）当A1v1＞2 时，E3是一个不稳定的结点。

证明：将E3带入式（12），得到系统Jacobian矩阵

（1）当0 ＜A1v1＜2 时，|λ1|＜1，在这种情况下E3是一个鞍点。

（2）当A1v1＞2 时，λ1＞-1，在这种情况下E3是一个不稳定的结点。

命题4当系统参数满足

时，E4是局部渐近稳定的。

证明：将E4带入式（12），得到系统Jacobian矩阵

在这种情况下，用特征值的方法来分析E4的稳定性比较复杂，因此我们用Jury 判据来分析。首先计算出E4处的特征方程

根据Jury 判据，当系统的参数满足下列条件时，E4是局部渐近稳定的，即

以上三个条件对应于特征值离开复平面中单位圆的三种方式。当P（1）＜0 时，J(E4)的一个特征值大于1，可能出现fold 分岔、跨临界分岔或叉式分岔。当P(-1) ＜0 时，J(E4)的一个特征值小于1，可能出现Flip 分岔。当1-Det(J(E4))＜0 时，J(E4)有一对复共轭特征值位于单位圆之外，可能出现Neimark-Sacker分岔。

3 数值模拟

上一节从理论角度较为详细地讨论了系统（10）所对应的均衡点在不同条件下的类型，并且通过Jury 判据给出了系统（10）唯一的Nash 均衡点E4的稳定条件。下面将从数值模拟的角度，利用单参数分岔图、双参数分岔图、吸引盆等工具来展示数值模拟过程中系统出现的动力学现象，并解释这些现象产生的原因及其背后的经济学意义。

3.1 委托参数αi 对于系统稳定性的影响

固定参数a=1.862 7，c=1.230 2，d1=-0.771 5，d2=-0.185 6，υ1=1.759 7，υ2=2.045 4。图1（a）（b）中，右侧色卡上的不同颜色代表了不同周期，考虑到计算误差问题，我们用黑色区域表示周期超过30以上状态，包括拟周期、混沌等。图1（a）展示了系统通向混沌的两种不同路径，结合右侧色卡，即系统依次通过1周期、2周期、4周期的倍周期序列（Flip分岔）通向混沌；或者直接从1 周期的区域经过Neimark-Sacker分岔进入混沌区域。在周期1以及周期2 之间的准周期区域，即Neimark-Sacker 分岔周围，动力学行为十分丰富，这些v-型岛，称为Arnold 舌。为了更方便地研究图1（a）中白色方框区域的复杂动力学行为，将图1（a）中的该部分放大，如图1（b）所示。在图1（b）中，白色数字表示与之相对应的Arnold舌的周期。不难发现，从下到上，大舌的周期呈奇数列递增排列，即5-7-9-11-…。周期5 与周期7之间有三个小舌，分别为周期12、周期17与周期19，周期17与周期19的舌分别位于周期12的舌的两侧，周期12 的舌称为周期17 与周期19 的父舌，周期17与周期19的舌称为周期12的两个子舌。我们发现，这种排列规律与Stern-Brocot 周期树（图2（c）所示）的排列规律一致，如图2（b）中的Stern-Brocot 树为Farey 树（图2（a））的衍生树，Farey 树是包含于Stern-Brocot 树的一棵左子树。将Stern-Brocot 树中每个节点上的分子与分母相加可以得到与之相对应周期树。除此之外，Stern-Brocot 周期树中，下层子树的周期和是上层主树的周期数的三倍。同样地，位于周期7 与周期9 之间的三个小舌也符合这种规律。随着参数α1的减小和参数α2的增加，这些舌将会重叠在一起，最终进入混沌。随着参数的变化，舌将会越来越窄，因此更高周期的舌的具体周期将很难识别，但由于这些舌具有分形的自相似性，可以推断系统的更高周期的舌依然是按照Stern-Brocot 周期树的排列规律排列的。

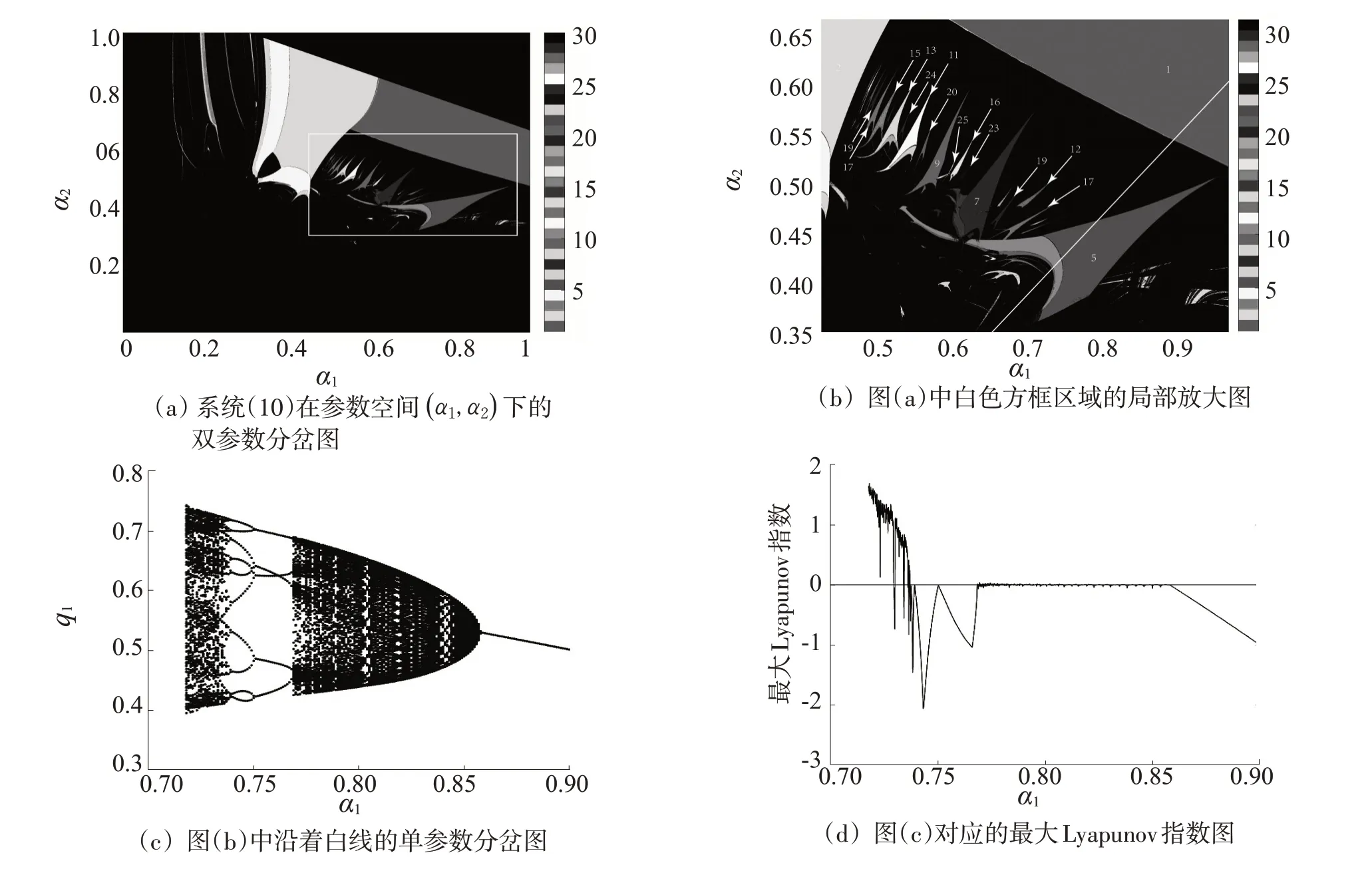
图1 分岔图与最大Lyapunov指数图

图2 六级二叉树

Arnold 舌通常出现在Neimark-Sacker 分岔周围，在舌与分岔的连接点处，Neimark-Sacker 分岔产生。即随着参数α1的改变，不动点将在这个尖点处通过Neimark-Sacker 分岔失去稳定性。图1 中展示了多种通向混沌的路径，如从两舌之间的拟周期状态进入混沌，或者在舌内区域，通过倍周期分岔进入混沌。如图1（c）与（d）分别展示了沿图1（b）中白色直线α1=1.154α2-0.449 8的一维分岔图和最大Lyapunov 指数图。即随着参数α1的增加，系统从混沌状态通过倍周期减半的方式进入周期5 的v-型岛，再通过准周期状态进入周期1的稳态。图1（d）中，α1≈0.858 3 时，系统对应的Jacobian 矩阵的两个特征值分别为λ1=-1.785 4+0.645 6i，λ2=-1.785 4-0.645 6i，（保留四位小数）因此，系统在α1≈0.858 3 时发生Neimark-Sacker 分岔，而当α1∈[0.768 4，0.858 3]时，系统的Lyapunov指数在0周围上下波动，由此可知，Arnold舌的出现意味着系统发生Neimark-Sacker分岔之后，并未直接进入混沌状态，而是在经历了一段时间的准周期状态后才走向混沌。

当α1在区间[0.6，1]，同时α2在区间[0.7，0.8]时，系统将处于一周期的稳定状态。通过以上分析可知，当两家公司的管理者同时将公司的利润最大化作为目标时，两家企业的竞争将处于一个相对平稳的阶段，在此期间，市场环境也将更加稳定。同时，经济市场的稳定也将为企业提供更多机会，企业也会专注于提高产品质量和服务水平上，由此形成良性循环。

3.2 调整速度vi 对系统稳定性的影响

两家企业的调整速度在相同的参数空间中对于系统的影响是相似的，为了简便，我们只选取其中一个进行研究。在此选取v1作为主要研究对象。固定一组参数：a=3.074 5，c=3.478 5，d1=-0.052 8，d2=0.899 4，a1=0.627 9，a2=0.450 4。从图3（a）可以发现，系统随参数v1、v2的增加可通过两种路径进入混沌，即Flip 分岔以及Neimark-Sacker 分岔；在1 周期与2 周期之间有许多Arnold 舌，因此推测系统在此区域之间可能存在多稳态现象。将图3（a）的白色方框区域放大（图3（b）），大舌的周期依次为7-9-11-13-…。在周期7与周期9的舌中间，有三个小舌，分别为周期16、周期23与周期25，16周期舌是23周期舌与25周期舌的父舌，且这两个子舌分布在父舌两侧。这些v-型区域周期数的排列规律依然符合Stern-Brocot 周期树的排列规律。一维分岔图可以看作是沿着二维分岔图中某一特定直线对应的分岔。图3（c）展示的一维分岔图即图3（a）中沿白色直线对应的分岔。对比图3（d）发现在区间[2.178，2.223]内，不同初值条件下，系统最终的演化状态会有很大不同。因此，企业在开始竞争时的不同选择，最终将会导致企业走向不同的发展道路。同时，在此区间内，出现了间断点，这种非常规的分岔行为也意味着系统可能在此存在吸引子共存现象，这种现象即上文中提到的多稳态。

在图3（e）-（h）中，将利用吸引盆来验证这种猜想，并在存在这种现象的情况下研究系统的演化规律，解释其中的动力学行为。图3（e）即当v1=2.186 9时，出现5 周期的吸引子与14 周期的吸引子的共存现象，它们对应的吸引域在图中分别用深灰色和白色表示。灰色区域为发散轨迹组成的逃逸区域，即不可行区域（下同）。图3（e）中，可行域中有许多形状不规则的“洞”，它们层层嵌套在深灰色和白色吸引域中。当参数增加至v1=2.198 5时，深灰色区域中的吸引子通过Flip 分岔由5 周期变为10 周期，同时白色区域中的吸引子的周期数减小，由14周期减为9周期，如图3（f）所示。此时，深灰色区域面积增大，星罗棋布地存在于白色区域中。随着v1的进一步增加，深灰色区域中的吸引子将通过一系列的倍周期序列，演化成如图3（g）所示的8 片混沌吸引子，同时其吸引域将占据可行域的大多数部分，白色吸引域中的吸引子则由9 周期变为之前的14 周期，同时其白色可行域的面积进一步缩小。当v1增加至2.206 6 时，周期9 的混沌吸引子变成图3（h）所示的芒果状吸引子，此时的可行域即将被深灰色区域所占据。若进一步增加v1的值，白色区域将消失。

因此，图3（a）中Arnold 舌的出现也意味着系统在此参数范围内存在多稳态现象，对应于图3（c）中的非常规分岔行为。而经由图3（e）-（h）数值模拟可知，这种现象确实是由于吸引子共存引起的。同时可发现，企业1的调整速度越大，会在市场竞争中失去越多的市场份额，不仅如此，过高的调整速度反而会促进竞争对手的发展。通过以上分析可知，当两家企业都避免频繁调整经营策略时，双方都能在博弈过程中占据一席之地，从而在满足自身利益最大化的同时实现共赢。

3.3 边际成本c 对系统稳定性的影响

非线性动力系统中，在其他参数不变的情况下，不同的初始条件将会影响到系统的最终状态。即给定不同的初值，在经过n次迭代之后，系统可能会收敛到一个不动点、多周期吸引子、不变环，或者是混沌吸引子。这种现象叫作“路径依赖”，即当前或未来的状态取决于过去所做出的决定，在非线性动力系统中反映为系统对初始条件的敏感性。

将参数固定为a=2.670 7，d1=-0.166 2，d2=0.827 7，α1=0.698 3，α2=0.898 4，v1=0.675 5，v2=1.107 1。当c=0.192 5 时，只有一种类型的吸引子，在图4（a）中其吸引域的颜色为深灰色。图中的白色区域为逃逸区域，即初值选在此区域中的点在经过n次迭代之后，最终将产生发散的轨迹。从图4（a）可以看出，深灰色的吸引域内嵌套了许多白色区域，这些云朵状的区域，称为“湖泊”，它们将深灰色吸引域变为复连通区域。将图4（a）中被矩形框起来的区域持续放大可以发现这些云朵状的“湖泊”具有自相似结构，如图4（b）（c）所示。虽然这些云朵状的“湖泊”无限接近深灰色吸引域的边界，但是它们始终没有与深灰色吸引域的边界相融合，因此，这些具有分形结构的“湖泊”形成了深灰色吸引域的弱分形边界。当c=0.167 时（图4（d）），出现了3周期的吸引子与吸引子共存的现象，不同于深灰色吸引域，此吸引域是不连通的，由3周期吸引子所在的直接吸引域（称之为“大陆”），以及与直接吸引域不相连的部分（称之为“岛屿”）组成。当c=0.156 9 时，3 周期的蓝色吸引子由三个不动点变成了三个不变环，如图4（e）所示。此时，系统（10）的Jacobian矩阵（保留四位小数）为

图4 吸引盆演化

其特征值为λ1,2=1.195 6±0.397 7i，此时特征值为复数且模大于1，这说明系统（10）通过Neimark-Sacker分岔失去了稳定性，因此，三周期吸引子由三个不动点变成了三个不变环。随着参数c的持续减小，当c=0.144 时，该吸引子变成了三片混沌吸引子（图4（f）），同时部分“大陆”与“岛屿”相连，这使得该吸引子的直接吸引域的面积增加。当c=0.124 1时（图4（g）），混沌吸引子所在的吸引域继续增大，同时混沌吸引子也即将与自身吸引域的边界发生接触，此时若进一步减小c的值，其吸引域将被深灰色的吸引域吞并。当c=0.122 时（图4（h）），吸引子与其吸引域边界发生接触，混沌吸引子消失，其吸引域也随之破裂。这是一种不同于局部分岔的全局分岔，即吸引子随参数变化不断膨胀，直到与自身吸引域的边界发生接触。当接触发生时，吸引子会突然消失，同时其吸引域也会被摧毁，这种现象也称之为“终极分岔”或者“边界危机”。它揭示了当参数接近临界值时系统状态的突变，此时，系统的不稳定性将增强，因此现实生活中应将参数的范围控制在合理范围内以避免全局分岔的产生。在本模型中，应将边际成本c的范围控制在0.122 之后，即c＞0.122 时，系统不会发生全局分岔，即系统将处于相对稳定的状态。但从图4（h）可以看出，刚刚消失的混沌吸引子的吸引盆的轮廓依然存在，此时，这些区域是由许多之前存在于其中的排斥子组成的稠密集，这些点多数发散，且这些排斥子的初值经过n次迭代之后产生的轨迹并不属于刚刚消失的混沌吸引子的吸引域，它们在分岔发生后可能收敛到新的吸引子或进入混沌状态。因此可以说，这些排斥子在收敛到另外一个吸引域之前，在刚刚消失的混沌吸引子的吸引域里停留了太长时间。

通过以上分析，结合图例可知，在该组参数下，企业1在竞争过程中的稳定域的面积始终都比企业2要小。边际成本c越大，越有利于企业2的发展，而企业1 则会在与企业2 的短暂共赢后逐渐失去竞争优势，率先进入混沌状态，随之将面临破产或者被其他企业兼并的风险。这种现象的产生可能是新技术的产生使得企业1相对于企业2而言，无法引进更多专业技术人员进入企业，或者是因为公司的总资本不够高，无法承担因单位产品成本的增加而产生的经济负担。

4 结论

本文建立了一个基于策略委托和相对利润的二维动态博弈模型。在两家企业都是有限理性的情况下，研究了系统均衡点的类型，并给出了使得系统唯一的Nash均衡点局部稳定的充分条件。

数值模拟结果表明，系统的参数对于系统稳定性的影响至关重要，当参数发生微小改变时，系统的状态可能会随之发生巨大改变。研究发现，此模型中，两家企业的委托系数越接近1，则系统的稳定性越好，表明当两家企业的代理人都将企业的利润最大化作为目标时，企业的发展就稳定。此外，两家企业的调整速度会彼此牵制，调整速度越大，市场进入混沌状态的时间点就越早，这就意味着其中一家企业将率先在竞争过程中面临危机。同时，边际成本对于两家企业的发展也至关重要，本模型中，边际成本越大，越有利于企业2的发展，这说明，企业1自身的资产水平或对市场新兴技术的适应能力等不如企业2，因此在竞争中将面临破产或被兼并。

本文运用单参数分岔图、双参数分岔图以及吸引盆来展示系统在博弈过程中产生的动力学现象，并结合非线性系统理论，分析了单参数分岔图中的间断现象与吸引子共存即系统的多稳态行为有关。双参数分岔图展示了系统通向混沌的不同路径，即Flip分岔或Neimark-Sacker分岔，并发现Neimark-Sacker分岔附近的分形舌的周期数符合Stern-Brocot周期树的排列规律。最后利用吸引盆内部结构的变化来研究系统的全局分岔行为，即吸引子与自身吸引域的边界发生接触，终极分岔将产生。以上结论可以帮助决策者更好地理解企业之间的竞争策略，并为制定相关政策提供理论支撑。通过分析动力学现象，决策者可以更好地预测市场变化和制定相应应对措施，从而优化企业在市场竞争中的表现。文中所用到的数据为大量数值模拟的结果，后续研究应以实际市场数据为主，以增加可行性。