中国水蚀区土壤可蚀性因子更新方法与应用

田芷源, 梁 音†, 赵 院, 曹龙熹, 赵 艳,4, 武逸杭,4

(1.土壤与农业可持续发展国家重点实验室,中国科学院南京土壤研究所,210008,南京;2.水利部水土保持监测中心,100053,北京;3.成都理工大学生态环境学院,610059,成都;4.中国科学院大学南京学院,211135,南京)

土壤可蚀性因子K是土壤流失方程的关键参数之一。K因子是侵蚀预报模型计算和水土流失动态监测的基础数据。K值的定义是在标准小区上单位降雨侵蚀力所引起土壤流失量的多少[1],反映土壤对侵蚀的敏感程度,其大小与土壤本身性质有关。

我国第1次水利普查时获得了全国范围首张K值分布图[2]。由于实测K值使用的径流小区建造昂贵,花费时间长且缺少统一的测量规范,能收集到的K值数据十分有限,因此利用经验公式对K值进行估算[3]。然而,使用的土种志数据距今已有近40 a,难以反映目前的土壤情况。为了获得更准确的K值结果,亟需在大范围内对计算K值的基础数据进行更新。

依靠有限样点很难满足越来越高的制图精度要求,因此还需探索一种能够实现高空间分辨率的K值点面扩展方法。以往研究在利用样点制作K值分布图时,常使用土壤图斑链接法及地统计插值[4]。然而,图斑链接法导致K值在土壤类型边界发生突变,且不能反映同一土壤图斑内存在的K值变异性[5]。使用地统计学方法对K值进行制图时,由于采样密度对插值精度影响较大,需空间结构因素大于随机部分才能得到较准确的结果,因此研究范围大多局限在流域尺度[4]。随着数字土壤制图的发展,遥感数据已被应用于K值空间预测,例如高程作为协变量被引入克里格插值进行K值制图[6],高程及植被作为空间变量可以提高K值的预测精度[7]。机器学习算法中的随机森林模型,是一种通过自助重采样技术对多个训练集随机选取特征变量,分别进行回归建模并平均多个预测值得到最终结果的方法[8]。该方法已被成功运用于预测土壤有机质含量、质地与土层厚度等关键土壤属性[9]。

为了实现全国土壤可蚀性因子更新目标,笔者提出一套基于近期汇编的中国土系志数据,利用随机森林模型进行点面扩展获得全国水蚀区K值分布图的方法,解决更新的2个关键问题:第一是如何获取全国地区最新的样点K值,第二是如何将样点的更新结果扩展至区域尺度。本次更新结果将有助于改善当前全国K值图数据陈旧及制图方法落后的问题。该成果可为土壤侵蚀预报模型提供基础数据,为年度水土流失动态监测工作提供服务。

1 材料与方法

1.1 土壤理化数据来源与处理

中国土系志数据是我国自第2次土壤普查以来最新且系统性的土壤调查数据[10]。全国土系调查项目于2008—2018年基于定量标准和统一分类原则开展系统性调查研究[11]。笔者基于各省份土系调查资料,收集并整理4 327个采样点的土壤剖面数据,查阅其调查地点(经纬度)和理化性质。其中有机碳质量分数通过除以系数0.58(采用Van Bemmelen因子,假定土壤有机质的含碳质量分数为58%)统一转换为有机质质量分数[12]。将数据进行预处理,主要采用加权平均的方法提取各样点0～30 cm耕层土壤的有机质和机械组成信息,当土体厚度<30 cm时则以实际厚度进行加权平均。

1.2 土壤可蚀性K值计算

采用全国第1次水利普查时K值的计算方法,使用通用土壤流失方程中的诺模图(Nomo)计算K值(Nomo-K)[2]。

K=(2.1×10-4M1.14(12-O)+
3.25(S-2)+2.5(P-3))/(100×7.593);

(1)

M=N1(100-N2)

(2)

式中:K为土壤可蚀性,t·hm2·h/(MJ·mm·hm2);O为土壤有机质质量分数,%;S为土壤结构系数(计算土壤粒径几何平均直径后查表所得,量纲为1);P为土壤渗透性等级(根据质地分类查表所得,量纲为1);M为质地指数,由N1和N2计算所得,%;N1为粒径在0.002～0.100 mm之间的土壤颗粒质量分数比例,%;N2为粒径< 0.002 mm的土壤颗粒质量分数,%。

由于全国土系调查中的质地分布仅包含砂粒(≥0.050～2.000 mm)、粉粒(≥0.002～0.050 mm)和黏粒(<0.002 mm)分级,Nomo公式计算时需要把已有土壤颗粒分析结果转化为极细砂质量分数(≥0.050～0.100 mm)。本研究比较了3种插值方法,分别是自然对数线性插值法、三次样条函数法、三次样条函数结合自然对数。计算过程如下:首先将各级别土壤颗粒质量分数累加计算得到小于某一粒径的质量分数(<0.002 mm、<0.050 mm、<2.000 mm),并计算该粒径对应的自然对数(ln(0.002)、ln(0.050)和ln(2.000))。自然对数线性插值法可建立颗粒累加质量分数与粒级自然对数之间的线性关系;三次样条函数法可建立颗粒累加质量分数与粒径之间的三次样条函数;三次样条函数结合自然对数法则可建立颗粒累加质量分数与粒径自然对数之间的三次样条函数。基于以上方法得到了<0.100 mm粒径所对应的质量分数,并将<0.050 mm和<0.100 mm粒径质量分数相减得到极细砂质量分数,通过分析极细砂质量分数的合理性和比较插值方程R2确定最优的插值方法。

当有机质质量分数>12%时,使用Nomo公式可能会导致负值出现,因此对有机质>12%的样点采用EPIC模型计算K值[3]

(3)

Sn1=1-Sa/100。

(4)

式中:Sa为粒径≥0.050～2.000 mm的砂粒质量分数,%;Si为≥0.002～0.050 mm 的土壤粉粒质量分数,%;Cl为粒径< 0.002 mm的土壤黏粒质量分数,%;C为土壤有机碳质量分数,%,通过有机质乘以转换系数58%所得;Sn1为土壤碳酸钙质量分数,%。

由于Nomo和EPIC公式的计算过程不同,采用EPIC公式得到的K值(EPIC-K)不能直接替代 Nomo-K值。因此,笔者使用线性、指数、幂函数和3阶多项式函数分别建立2种公式计算K值的转换关系。比较4种拟合方程的R2,除线性方程拟合精度略低以外(0.795 5),其他3种非线性方程的拟合精度十分接近(0.806 4～0.807 2)。从趋势来看,Nomo-K和EPIC-K值之间并非简单线性关系,随着EPIC-K值的增大,Nomo-K值出现先缓慢增加后快速增加的趋势。这与指数方程所显示的规律是一致的。总之,当土壤有机质≤12%时,使用Nomo公式计算K值;当有机质>12%时,采用EPIC公式计算K值并利用其与Nomo-K值的指数关系式进行修正。

1.3 环境因素分布图收集与处理

沿用在太湖流域片预测K值时使用的遥感方法获取的环境因子指标作为预测变量,包括气候、地表温度、植被、光波、地形和母质[13]。由于随机森林模型具有避免过拟合的优势,且模型训练集样本量足够大,没有对环境因子进行剔除。

各项环境指标的空间分辨率从30 m到1 km不等,通过最邻近法将所有指标统一重采样为30 m分辨率后进行叠加运算。由于气候和地表温度在较小尺度下不存在大的差异,重采样后在1 km范围内气候及地表温度值不变符合实际情况。各样点对应的环境变量值通过坐标位置提取。

1.4 土壤可蚀性K值制图

采用随机森林回归方法建立K值预测模型。首先对样点的环境要素及K值进行训练,然后利用多源遥感影像将建立起K值预测模型推广至全国地区,完成K值由点及面的反演计算。其中模型的2个关键参数通过调参选择:模型误差随着决策树数量(ntree)的增加而降低,当决策树数量超过400以后,模型误差趋于稳定,因此选择使用默认参数ntree=500;随机森林节点变量数(mtry)一般选择环境变量数的1/3(本研究对应mtry=20),通过对节点变量数在mtry=20左右逐个比较模型精度,确定最佳的mtry值为17。

K值预测模型的建模精度通过外部验证的方法进行评估,采取常用的5折交叉验证法,重复100次取平均值作为评价结果。评价指标包括决定系数 (R2),均方根误差 (E1)以及平均绝对误差 (E2),计算公式如下:

(5)

(6)

(7)

式中:n为训练样本个数;Yi为观测K值;i为模型预测K值;为平均观测K值。

基于K值预测模型,以61项环境因子空间分布图作为自变量,使用随机森林方法进行预测,输出全国尺度K因子栅格图,K值更新图的空间分辨率为30 m×30 m。

1.5 数据处理与统计分析

研究利用Excel 2019计算样点Nomo-K值与EPIC-K值,并建立两者的回归关系;利用ArcGIS 10.8处理空间数据,包括投影转换、空间重采样,提取样点对应的环境变量,统计栅格极值、平均值及标准差等;利用R语言编程实现土壤粒径的批量插值转换,同时构建随机森林回归模型,进行全国范围K值的空间预测。在分析K值分布规律时,土壤类型图使用1995年编制的《1∶100万中华人民共和国土壤图》。

2 结果与分析

2.1 土壤质地插值转换

插值获得诺模图计算所需极细砂的质量分数,以江西省关山系样点为例,使用3种插值方法得到粒径质量分数结果如表1所示。其中,自然对数线性插值法拟合精度较差,获得的<0.100 mm粒径质量分数低于<0.050 mm粒径,导致极细砂质量分数为负值;三次样条函数法受样本数量过少(n=3)的影响,获得的累加极细砂粒径(<0.100 mm)质量分数高于100%,明显不合理;三次样条函数结合自然对数法克服了函数分布不合理的缺点,以高精度方程拟合了不同土壤粒径的质量分数(R2≈1),同时避免了质量分数高于100%的情况(图1)。

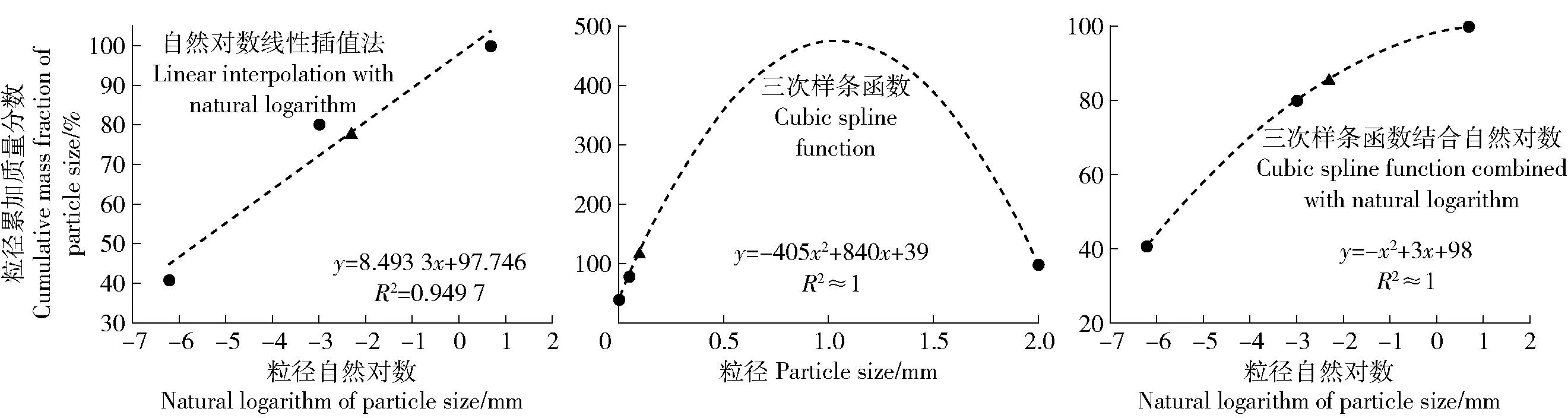
圆点为已知粒径质量分数,三角形为预测粒径质量分数。下同。The dot represents the known particle size mass fraction, and the triangle represents the predicted particle size mass fraction. The same below. 图1 土壤质地插值转换方法对比Fig.1 Comparison of soil texture interpolation conversion methods

表1 土壤质地插值转换结果对比(江西关山系)Tab.1 Comparison of soil texture interpolation conversion results(Guanshan series in Jiangxi)

在少数样点中,土壤<0.050 mm和<2.000 mm的粒径质量分数十分接近,使用三次样条函数结合自然对数法计算所得<0.100 mm的粒径结果可能略高于100%。针对这种情况,以山东省小岛河系样点为例(图2),利用线性函数在<0.050 mm和<2.000 mm分段之间插值得到<0.100 mm的粒径质量分数,线性插值使<0.100 mm粒径质量分数既小于<2.000 mm粒径质量分数,也大于<0.050 mm粒径质量分数,能确保结果的合理性。

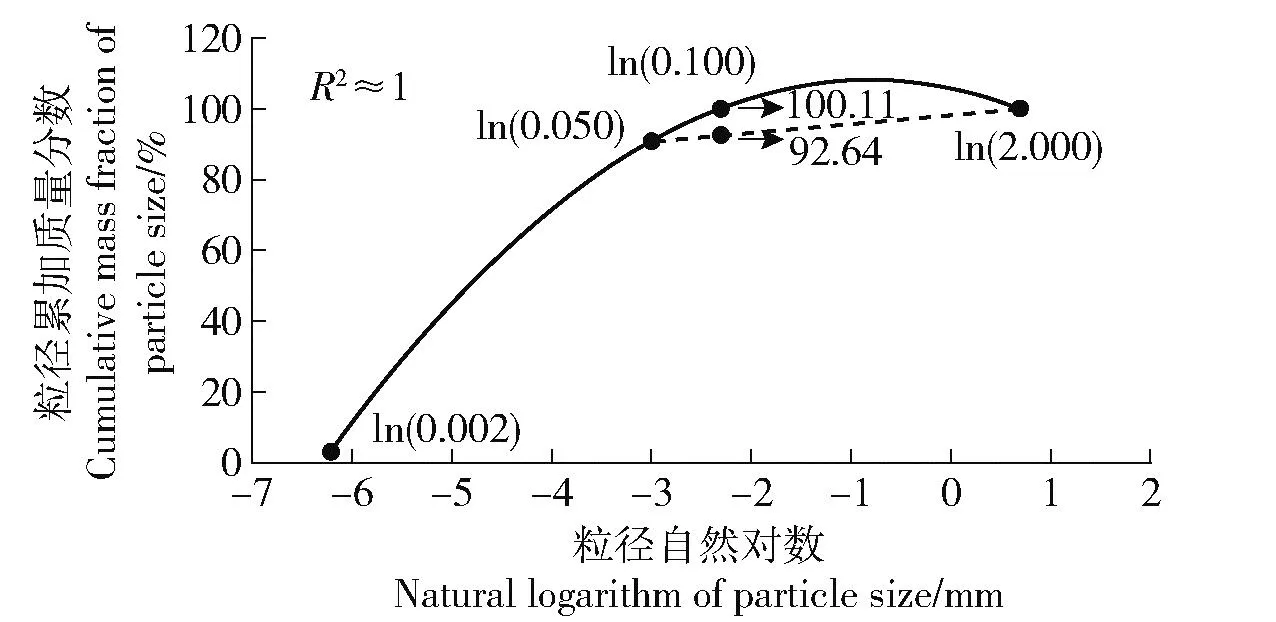
实线为三次样条函数结合自然对数法拟合,虚线为自然对数线性插值法。The solid line is cubic spline function combined with natural logarithm, and the dotted line is linear interpolation with natural logarithm. 图2 土壤粒径插值结果过高处理Fig.2 Processing of excessive soil particle size interpolation results

2.2 土壤可蚀性K值的计算与预测模型

采用Nomo和EPIC公式分别计算4 327个土系样点K值,统计结果如表2所示。EPIC计算K因子的最小值比Nomo-K值大,最大值比Nomo-K值小,且标准差更小,EPIC计算K值的平均值及中位数比Nomo-K值大16%。因此,不能直接使用EPIC-K值替换高土壤有机质条件下的Nomo-K值。

表2 全国土壤可蚀性K值计算结果统计Tab.2 Statistics of calculated results of soil erodibility K value nationwide

建立2种公式的转换关系时,R2均>0.79(图3),但散点图显示随着EPIC-K值的增大,Nomo-K值出现先缓慢增加后快速增加的趋势,这与指数方程的规律相符。最终选择该方程对全国有机质>12%的55个样点进行K值修正。这些样点主要分布在东北和青藏高原的湿润或者滞水条件下,采样部位在上、中、下坡和台地均有分布,表明并非沉积导致K出现负值。根据定义,K因子为在标准小区上由单位降雨侵蚀力所引起土壤流失量的多少[1]。土壤流失量不可能为负数,所以K值不应存在负值的情况。校正前55个样点的EPIC-K均值为0.034 4,校正后均值为0.026 6,弥补了EPIC-K值大于Nomo-K值的差异。

EPIC-K is soil erodibility calculated by EPIC model. Nomo-K is soil erodibility calculated by Nomo formula.图3 土壤可蚀性K值计算结果拟合方程对比Fig.3 Comparison of fitting equations for the calculated results of soil erodibility K

以土系调查项目所建立的更新K值作为因变量,以包含气候、地形、植被、母质类型、地表温度、可见光及近红外波段在内的61项环境因子指标作为自变量,在mtry=17,ntree=500的模型参数下,建立的全国K因子随机森林预测模型,运用5折交叉验证方法重复100次的评估结果为:R2=0.381,E1=0.012 47,E2=0.009 63。这与太湖流域片建立K值模型的精度类似[13],但低于使用随机森林预测土壤有机质和全氮的空间分布[14]。这与本研究采样密度稀疏、空间建模尺度大以及缺乏与K值强相关性的预测变量等原因有关。

2.3 全国土壤可蚀性K值分布规律

全国K因子分布范围在0.005 1～0.074 5之间,这与前人在样点尺度建立的我国主要土壤K因子分布范围0.000 8～0.070 5相似[15]。分布趋势呈现出华北平原和黄土高原地区高,天山地区及东北平原次之,南方山地丘陵、青藏高原及内蒙古高原较低的规律。这与其他学者总结的我国土壤可蚀性分布规律相似[16],但该研究发现青藏高原的K值最高。也有研究发现青藏高原K值比黄土高原、川渝地区和滇东北地区的K值略低[17],这可能是由于青藏高原K值存在较大差异所造成的。

进一步利用水土保持一级区划分析全国更新K值的分布规律,发现更新K值在西北黄土高原区和北方土石山区较大,在青藏高原区最小(表3),这与自然及人为活动等因素的综合作用有关。其中,西北黄土高原区土壤有机质含量普遍很低因此K值偏高[18];北方土石山区长期以来受人类耕作活动的影响导致K值较高;青藏高原区由于地形落差大,K值具有垂直地带性,在少量低海拔河谷地带K值较高,而在大面积的高海拔地区由于成土作用弱K值明显降低[17]。此外,东北黑土区在风砂土分布地区K值最大,在黑土集中的漫川漫岗地带由于农耕活动导致K值较大,暗棕壤分布的大兴安岭及长白山等地K值较小。

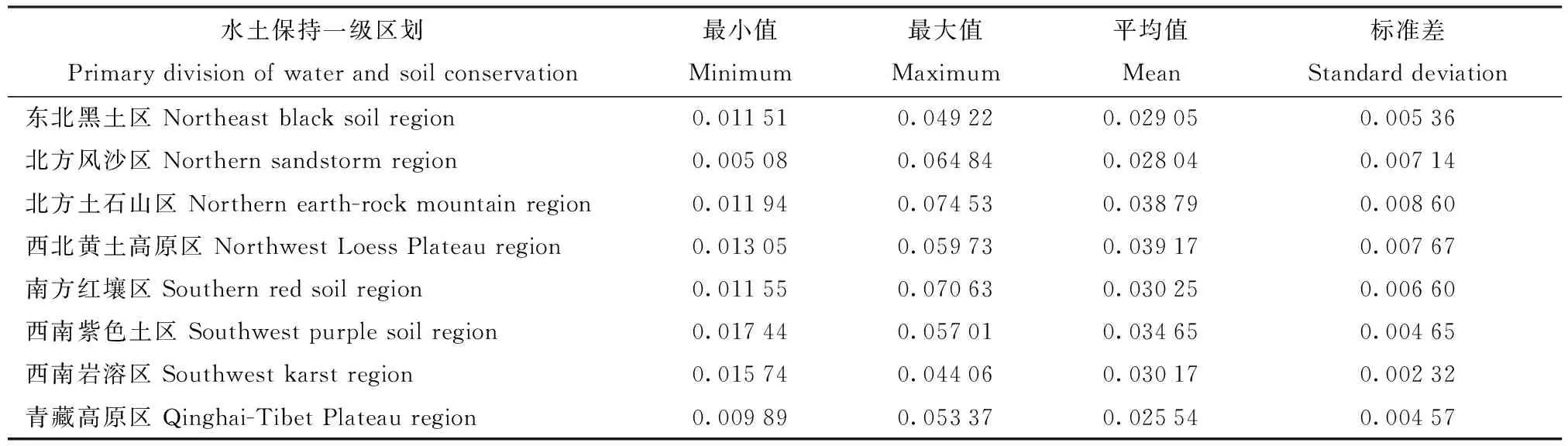
表3 土壤可蚀性更新K值在水土保持一级区划的统计Tab.3 Statistics of soil erodibility update K value in the first level zoning of soil and water conservation

K值的空间分异与我国主要土壤类型的分布情况有关,前人曾报道黄土高原的黄绵土和东北的黑土K值较大,南方红壤K值较小[15,19]。本研究从主要土壤类型统计来看,黄绵土和潮土的更新K值较大,平均值均超过0.04,而高山土的平均K值最小,其次为栗钙土、暗棕壤和红壤,均不超过0.03(表4)。分析原因认为黄绵土和潮土的粉粒含量较高,土壤更容易遭受侵蚀。此外,潮土K值的标准差最大。前人研究发现,同一种土壤下不同母质和植被覆盖可以通过影响土壤的水稳性从而改变土壤的抗蚀能力[20],因此相同土壤类型下K值的差别也可能很大。

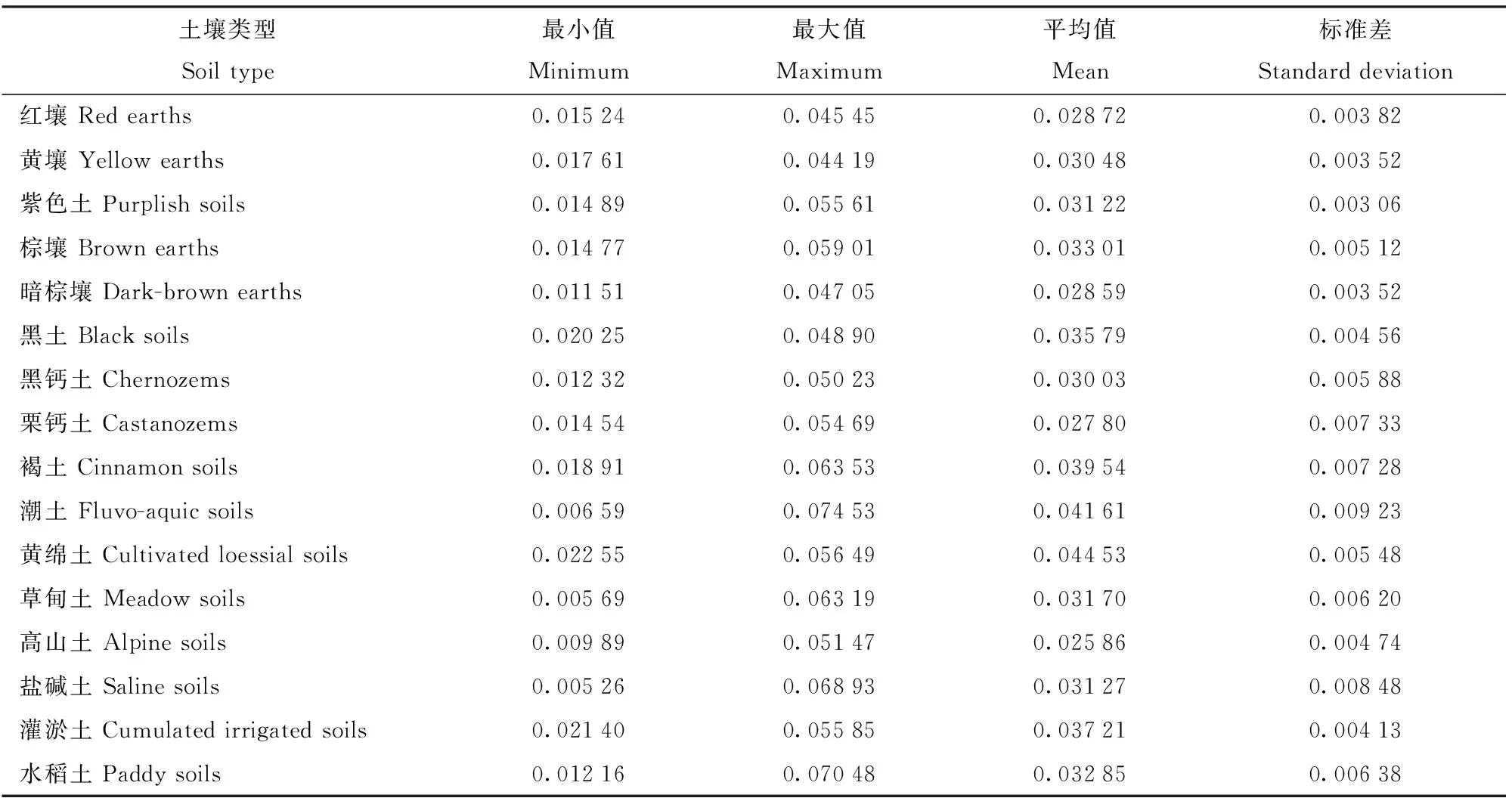
表4 主要土壤类型下土壤可蚀性更新K值统计Tab.4 Statistics of updated K values of soil erodibility under main soil types

值得注意的是,由于Nomo和EPIC模型是基于美国土壤实验所建立的,在中国地区存在适用性问题。张科利等[19]利用径流小区观测资料在我国东部地区建立了K值的校正公式,分别为K=-0.033 36+0.744 88KNomo(R=0.721),K=-0.013 83+0.515 75KEPIC(R=0.613);更进一步说,Nomo模型在黄土高原和黑土区的应用效果(R2=0.55～0.60)要优于红壤和紫色土(R2=0.11～0.37),EPIC模型除黑土区以外(R2=0.05)在其他地区的应用效果较好(R2>0.58)[21]。直接应用本研究结果可能会对K值产生不同程度的高估,因此需要在全国范围内进一步收集实测资料将K值校正以后用于土壤侵蚀模数计算。

3 结论

1)本次更新进一步完善了全国土壤可蚀性因子计算方法。本研究在美国制砂粒、粉粒、黏粒机械组成实测值的基础上插值得到极细砂质量分数,基础数据更为准确;通过计算土壤粒径几何平均直径来获取结构系数,更具有客观性;建立于全国统一的土系基础数据库,消除了不同省份之间的系统误差;以30 m分辨率栅格为制图单位,更为详细地表达K值的空间变异情况。

2)全国土壤可蚀性更新K值的空间分布呈现出以下规律:黄土高原区和北方土石山区居高,西南紫色土区、南方红壤区、西南岩溶区、东北黑土区和北方风沙区次之,青藏高原区最小。这主要是由于不同土壤类型在各地区的分布所造成的。统计可知黄绵土和潮土的K值较大,红壤、暗棕壤、栗钙土的K值较小,高山土的K值最小。

3)本研究采用的Nomo和EPIC公式都是基于美国土壤建立的K值计算经验公式,可能与实际监测的K真实值有差距。因此需要积累我国不同地区标准径流小区的长期观测资料,使用年平均侵蚀量和降雨侵蚀力因子进一步率定K值,以期建立起实测值与经验公式计算值之间的关系式或直接建立适用于我国的土壤可蚀性计算公式。