基于DBSCAN聚类的异构多智能体分层任务分配方法

张学军，徐红丽，李祥民，白 洁，郝东强

（1. 中国电子科技集团公司第五十四研究所，石家庄 050081；2. 东北大学机器人科学与工程学院，沈阳 110819）

1 引 言

伴随着多智能体技术和信息技术的发展，新的探测需求不断产生，在多智能体的约束下，更多的挑战也不断涌现，相关研究方向也被不同学者广泛关注［1］。当利用多智能体集群对多待探测点进行遍历探测时，探测任务的分配问题是一个较为经典的研究方向［2］。对应不同的使用场景，多智能体集群的任务分配可分为动态、静态任务分配两种［3］。在对动态目标进行探测时，常使用动态任务分配方式，因为此时待探测区域是未知的，探测任务总是不断出现，所以只能边探测、边分配任务，很多学者也在相关领域进行了研究。例如，Bertuccelli 等针对传感器存在噪声的多智能体作战场景问题，提出了一种基于增强CBBA（Consensus Based Bundle Algorithm，基于共识的捆绑算法）的动态任务规划算法［4］。Capitan等针对多阶段不确定条件下的规划问题，提出了一种基于马尔可夫决策过程（Markov Decision Process，MDP）的动态任务规划算法［5］。上述问题没有全局信息，任务分配时会着重考虑机器人的探测能力、通信延迟和能耗分配等因素［6-7］。在对静态任务进行分配时，相关问题通常被建模为旅行商问题。例如，Abbasi 等人提出了启发式舰队合作算法，用以解决海洋棘冠海星集群处理问题［8］；Hooshangi 等提出了一种结合区间数VIKOR（多准则妥协解排序）和基于合约网络协议（Contract Net Protocol，CNP）拍卖机制的多智能体任务规划方法，用来解决灾害环境中的救援问题［9］。上述工作通过使用能力更强的多智能体单元对待探测区域进行预扫描，凭借能力更强的实验平台改善了上述探测和能耗方面的部分缺点，然后再用多智能体集群进行探测任务，但是上述工作一方面需要大量可执行通信和探测任务的多智能体单元，耗费偏高，且数量较少，每个多智能体单元分配的任务点数量较多，任务分配算法的计算效率和探测效率都比较低［10-11］。截至目前，不同场景下的探测任务仍然面临很多问题，使用通信/探测的异构多智能体集群组合，对面向预探测后区域中的大规模探测点进行任务分配的工作还鲜有研究。

研究面向大规模探测点的异构多智能体集群组合的任务分配问题可以带来很多好处，例如在能耗方面，异构多智能体单元组合各司其职，可实现更小的能源消耗，延长多智能体集群的工作时间［12］；在任务分配效率方面，负责通信的多智能体单元计算能力较强，可搭载更强的计算模块，大幅提高任务分配效率［13］；在经济方面，执行近距离探测任务的小型多智能体单元所配置传感器的成本较低，和探测能力强的大型多智能体单元组合使用，能够节省成本；在探测效率方面，异构集群可在单位时间内探测更多的点位，增加单位时间内的探测区域［14-15］。

但在研究过程中，仍面临如下三个挑战：首先是多智能体单元任务分配的均衡问题，考虑到随着传感器能力和探测需求的增加，预探测得到的点的数量越来越多，如何合理分配探测点给每个多智能体单元组群是一个挑战。其次是异构多智能体单元间的配合问题，因为异构多智能体单元的功能各不相同，探测和通信等功能的多智能体单元需要在时间和空间域上进行协同，所以异构多智能体单元间的协同配合是一个挑战。最后，多机器人任务分配问题是一个典型的NP-hard 问题，所以如何高效进行任务分配是一个挑战。为了攻克上述挑战，本文提出了一种新颖的基于聚类的混合求解方法（Cluster-based Hybrid Solution Method，CHM）。相比于直接使用遗传算法（Genetic Algorithm，GA），该算法首先对所有任务节点进行聚类，其次设计了一套全局与局部相结合的分层任务分配算法，最后提出了一种异构多智能体单元配合算法。本文的贡献如下：

（1）提出一种基于通信距离约束的基于密度的聚类（Density-Based Spatial Clustering of Applications with Noise，DBSCAN）等效算法，对大规模任务进行分组等效处理。

（2）提出一种异构多智能体单元任务配合方法，可使异构多智能体单元系统在探测、通信共同约束下进行工作。

（3）针对虚拟的预探测点进行了大量的仿真模拟实验，进一步验证了算法的有效性和实用性。

2 问题表述

某片区域存在N个待处理目标任务点tpi，构成待处理的任务集合TP为

式中，tpi={x，y}i，x和y表示目标任务点位置坐标信息。

现有M1个通信单元cu，M2个执行单元eu构成的集群单元U为

式中，执行单元cu主要负责执行具体的任务，通信单元eu主要负责给执行单元提供通信支援，不需要直接参与任务执行。执行单元在执行任务时，通信单元需要在执行单元通信范围内提供通信支持。

通信距离约束可表述为

式中，Ci，j表示通信单元cui和执行单元euj之间是否可以建立通信，Ci，j= 1 表示通信单元可以和执行单元之间建立通信，反之则表示不能；di，j表示通信单元cui和执行单元euj之间的距离，r表示通信单元cui的通信半径。

执行任务能力约束可表述为在时刻t时，执行单元euj只能访问一个任务节点，即

优化目标为移动总距离

表示期望参与所有任务的装备单元移动的总距离能够最小，式中Lcui表示通信单元cui移动的总距离，Leuj表示执行单元euj移动的总距离。

3 集群协同任务分配求解框架

执行单元和通信单元需要协同完成对所有任务点的处理，且执行单元与通信单元之间存在通信距离约束，受限于当前算力水平，直接进行任务分配求解很难在有限的时间内得到相对最优的任务分配结果。本文求解集群协同任务分配问题的流程如图1所示。

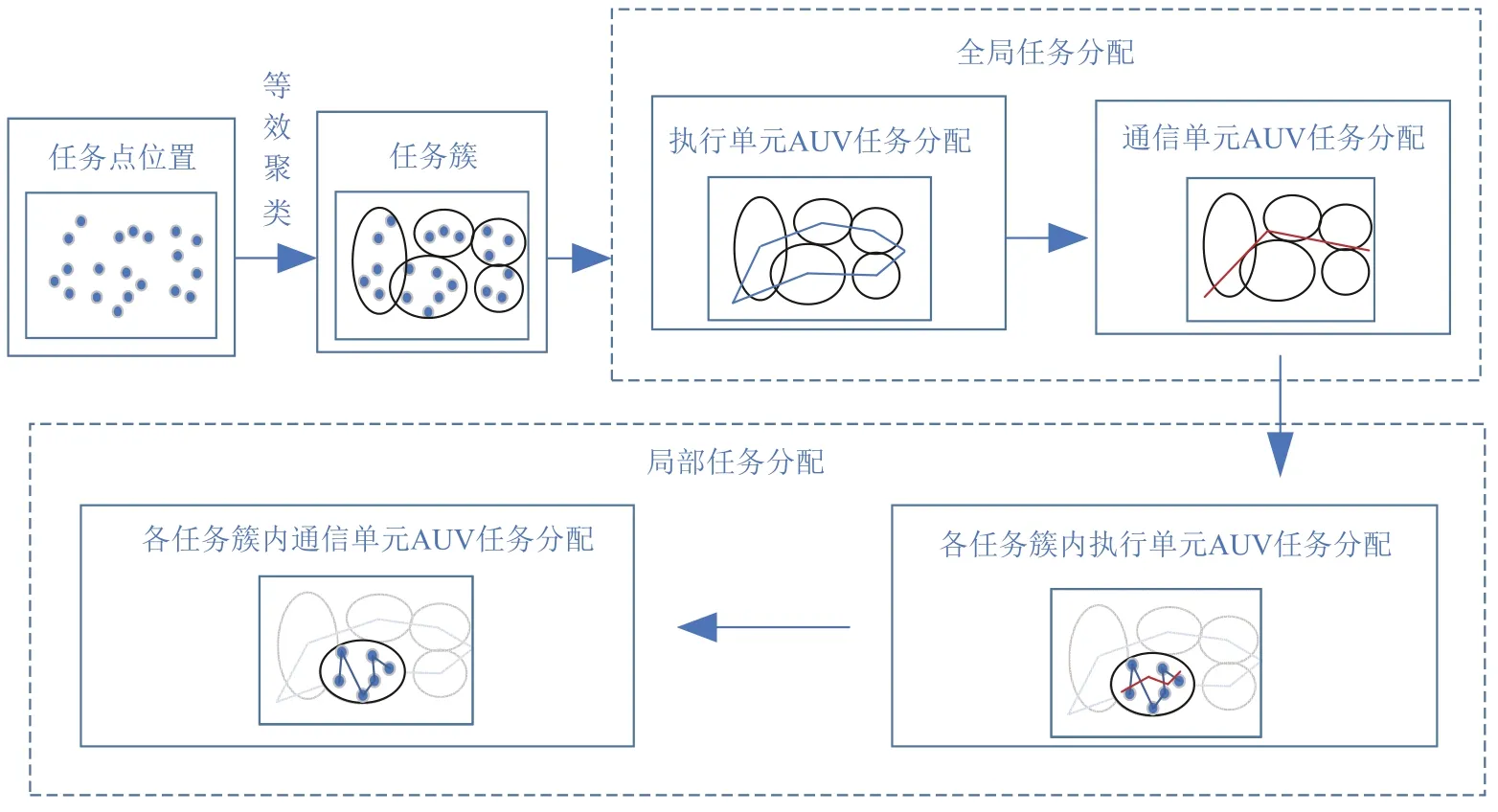
图1 求解流程Fig.1 Solution process

首先根据疑似目标节点的位置分布，按照通信距离约束信息对目标任务节点进行DBSCAN 聚类，并将聚类到一起的目标任务节点定义为一个任务簇。然后根据每个任务簇包含的目标任务节点属性特征信息并结合装备单元能力特征信息对所有任务簇进行等效模糊处理，得到能反映内部各疑似目标节点信息的新的等效任务节点。接着根据得到的新的任务节点分别对通信单元和执行单元进行全局任务分配。执行单元任务分配问题可转化为多旅行商问题，然后采用遗传算法进行求解，通信单元任务分配问题需要考虑执行单元在各个任务簇的时间信息，因而可以将其等效为带时间窗口的多旅行商问题并采用遗传方法进行求解。在完成针对通信单元和执行单元的全局任务分配后，需要针对每个任务簇内部所有目标任务节点进行任务分配，执行单元任务分配问题等效转化为旅行商问题，采用遗传算法进行求解。然后根据执行单元的访问目标任务节点序列，规划通信单元的虚拟访问节点，从而完成执行单元和通信单元的局部任务分配。

3.1 聚类

考虑到通信约束的影响，执行单元必须在通信单元附近选择可执行的任务点，同时当任务规模变大，整体优化将变得更加复杂，因此首先考虑通过通信距离约束将任务进行分组，从而将大规模任务与资源配置分配问题变成局部小规模问题，并以此来降低计算量。采用DBSCAN 方法对任务点进行分组，

式中，gi={tp1，tp2，…，tpl}，表示第i个任务簇有l个目标任务点，k表示分组后的任务簇数目。

首先根据聚类结果和任务簇gi群组内目标任务点tpi的分布情况，将其等效转化为一个节点，然后对执行单元euj完成任务簇gi的移动距离和耗费时间做等效近似处理。

任务簇gi等效节点Ex，y(gi)位置坐标为

式中，fr(gi)表示包含任务簇gi内所有目标任务节点tpi的最小覆盖圆的圆心坐标。

执行单元访问完任务簇gi内所有任务目标节点tpi的等效近似移动距离Ed为

执行单元完成该群组的等效近似时间Et为

3.2 全局任务分配

3.2.1 执行单元任务分配

通过聚类将满足通信约束的任务点聚类为若干个可供执行单元组选择的任务簇gi，此时全局执行单元euj任务分配问题为多旅行商问题，将所有执行单元的最小移动距离作为优化目标函数，采用遗传算法求解每个执行单元相对最优的任务簇访问序列结果。优化目标形式为

3.2.2 通信单元任务分配

通信单元需要和执行单元协同完成对任务点的处理，根据执行单元的全局分配结果对通信单元进行任务分配，由于各任务簇的任务数量不同，执行单元在处理各任务簇时需要的时间也各不相同，因而通信单元到达各个任务簇节点存在的时间约束为

式中，wj= max(0，ei-aj)，aj是通信单元到达任务簇节点的时间，wj表示通信单元等待的时间，ej表示执行单元开始执行第j个节点的时间，Δij表示通信单元从节点i到达节点j的时间。

根据各个任务簇的时间约束，此时通信单元的全局任务分配问题为带时间窗口的多旅行商问题，将所有通信单元cui的最小移动距离作为优化目标函数，采用遗传算法求解每个执行单元的相对最优访问任务簇序列。优化目标函数的形式为

3.3 局部任务分配

在执行任务过程中，通信单元不直接参与对任务点的处理，仅负责与执行单元完成通信，即不需要到达任务点位置。群组内任务分配首先采用遗传算法对执行单元进行任务分配，然后根据对执行单元的任务分配结果对通信单元进行任务规划。

3.3.1 执行单元局部任务分配

执行单元的局部任务分配问题属于固定起止点的旅行商问题，将执行该任务簇的执行单元最小移动距离作为优化目标函数，然后采用遗传算法求解相对最优的目标任务节点访问序列。优化目标函数设置为

式中，disi，j表示从目标任务节点tpi到目标任务节点tpj之间的距离。遗传算法求解步骤如下：

关于交叉变异操作，则是根据生成的执行单元访问目标任务节点的父代个体序列，生成两个不大于父代个体序列长度的随机数，进行几种类型交叉操作，如图2所示。

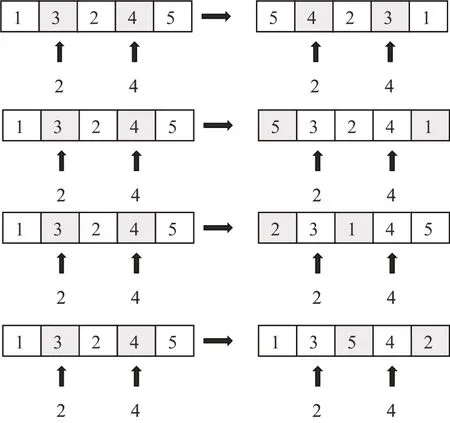
图2 两个基因位置交换交叉操作示意图Fig.2 Schematic diagram of crossover operation of two gene positions

变异操作则是舍弃原父代个体，重新生成一个新的子代个体，如图3所示。

图3 变异操作示意图Fig.3 Schematic diagram of mutation operation

3.3.2 通信单元局部任务分配

由于通信单元不需要到达任务位置点，因而根据执行单元处理的任务位置点添加虚拟节点vx，y，来规划通信单元的访问节点位置。虚拟节点添加情况类型如图4所示。

图4 虚拟节点类型示意图Fig.4 Diagram of the virtual node type

类型Ⅰ：当任务簇gi内部所有任务节点tpi都在执行该任务簇的通信单元cui通信范围内，有

式（14）、式（15）表示此时虚拟节点vx，y的坐标为包含任务簇gi内所有任务节点tpi的最小覆盖圆的圆心坐标。

类型Ⅱ：当任务簇gi内部部分任务节点tpi都在执行该任务簇的通信单元cui通信范围内时，根据执行单元euj执行任务节点顺序，对当前任务组任务节点进行二次分组为

式中，g′i={tpj|di，j≤r}，g′i表示对任务簇单元gi内任务节点tpi根据通信单元cui通信范围重新聚类而成的新的小任务簇，a表示对任务簇gi二次聚类生成的新的任务簇数目。

此时虚拟节点为

4 实 验

本文算法仿真计算机配置为：CPU型号为Intel（R） Core（TM） i7-6500U CPU@ 2.50 GHz 2.59 GHz，内存8.00 GB。

设区域大小为10 km×10 km，执行单元数目为3 个，通信单元数目为2 个，通信距离为300 m，执行单元移动速度为2 m/s，通信单元移动速度为4 m/s，实验结构如表1～3所示。

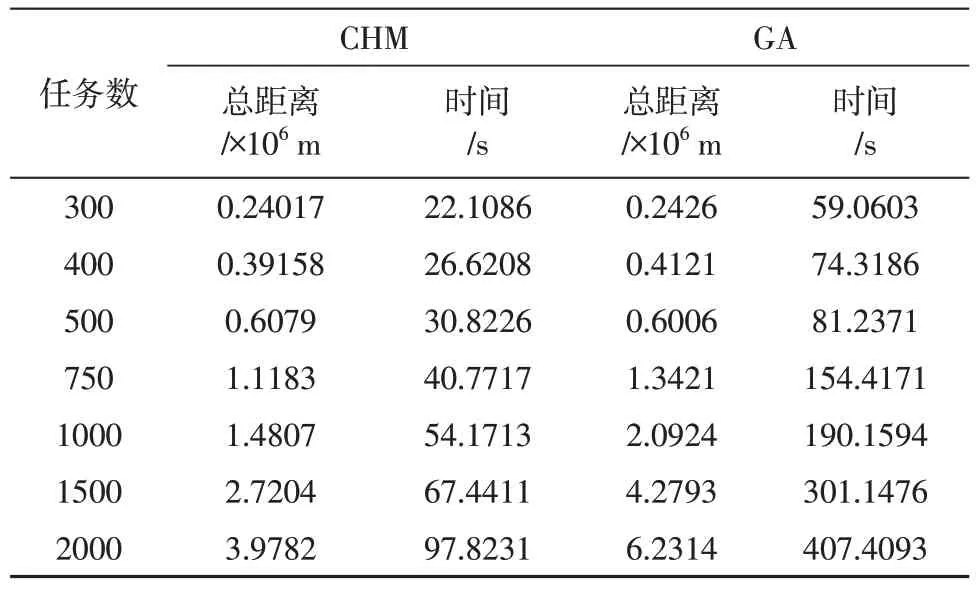
表1 任务簇数目约为40时不同规模任务节点数Table 1 Comparison of the number of task nodes of different sizes when the number of task clusters is about 40

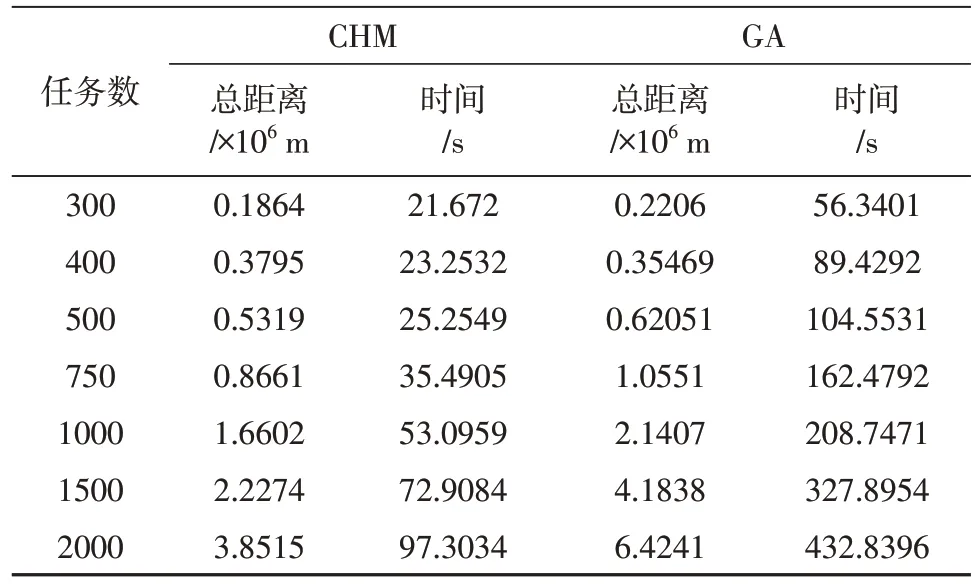
表2 任务簇数目约为50时不同规模任务节点数Table 2 Comparison of the number of task nodes of different sizes when the number of task clusters is about 50

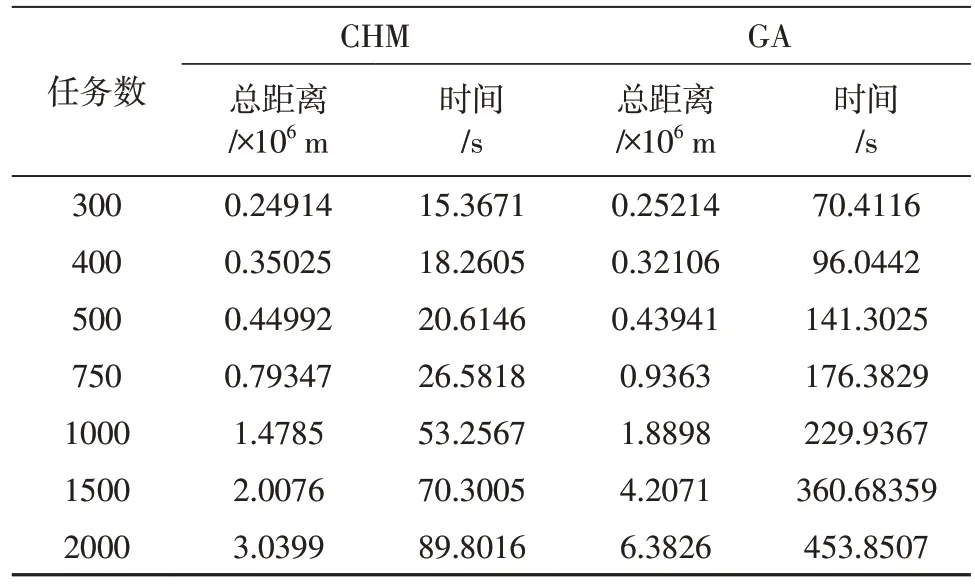
表3 任务簇数目约为60时不同规模任务节点数Table 3 Comparison of the number of task nodes of different sizes when the number of task clusters is about 60

图5和图6分别表示不同任务规模和求解时间及移动总距离之间的关系，通过实验结果可知，在10 km×10 km区域内，当目标任务节点数小于等于500 时，在求解得到的移动距离相近的情况下，本文算法所用的求解时间相较于直接使用遗传算法提升了70%以上。当任务节点数大于500 时，随着任务节点数的增加，本文方法求解得到的相对最优解明显优于直接使用遗传算法，而且求解时间减少了6 倍以上。这足以说明，本文所提出的方法在求解大规模集群协同问题上能够有效求解相对最优的任务分配结果。

图5 目标任务节点数与求解时间之间关系Fig.5 Relationship between the number of target task nodes and the solving time

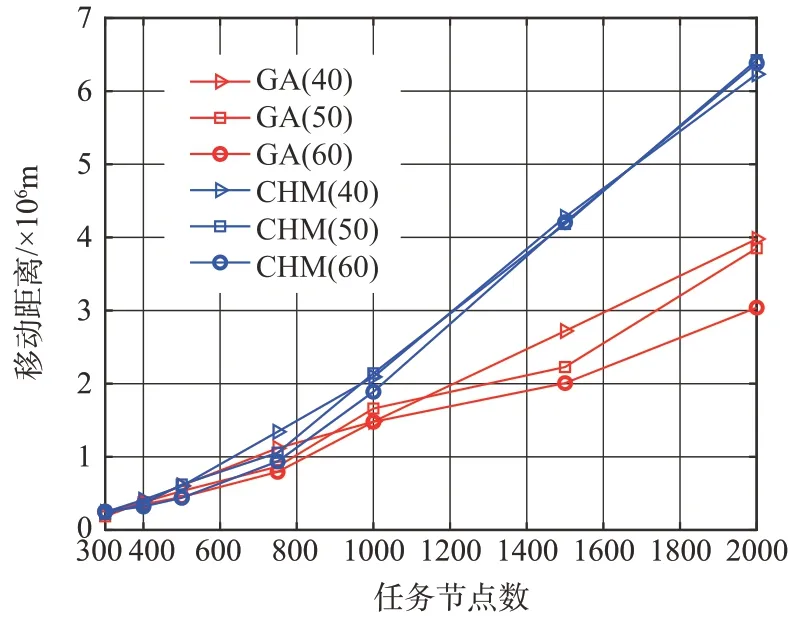
图6 目标任务节点数与移动总距离之间关系Fig.6 Relationship between the number of target task nodes and the total distance moved

以10 km×10 km 区域1000 个任务节点为例，3 个执行单元和2个通信单元协同任务分配结果如图7～9所示。

图7 执行单元访问任务节点序列示意图Fig.7 Schematic diagram of execution unit access task node sequence

图7、图8 分别表示3 个执行单元遍历访问1000 个任务节点情况和2 个通信单元协同遍历访问虚拟节点情况。图9表示执行单元和通信单元协同访问节点序列，执行单元依次遍历图中所有任务节点，通信单元根据执行单元访问任务节点序列，同步规划遍历图中虚拟节点，协同完成整个任务。从图中可以看出，本文所提算法能有效解决具有通信约束的多异构集群协同任务分配问题。

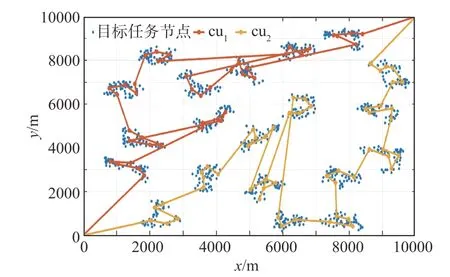
图8 通信单元访问任务节点序列示意图Fig.8 Schematic diagram of communication unit access task node sequence

图9 执行单元与通信单元协同访问节点序列示意图Fig.9 Schematic diagram of execution unit and communication unit co-access node sequence

5 结 论

本文针对具有通信距离约束的多异构集群大规模协同任务分配问题中存在的任务规模大、协同复杂难点，采用分而治之和全局与局部相结合的思想，提出了一种聚类和启发式算法相结合的方法。实验结果表明，相较于直接求解方法，本文所提算法不仅解决了大规模集群协同任务分配问题，还可以在保证优化目标值相近的情况下，缩短70%以上的求解时间，较快得到相对最优的任务分配结果。此外，本文所提方法不仅适用于水下场景的多异构集群的协同任务分配问题，而且也可以扩展应用到农业领域的无人机集群采摘任务作业问题等。目前，本文所研究的集群任务分配问题聚焦于具有聚集特点的任务分布形式，然而在现实中任务分布形式多种多样，未来将继续研究在不同分布形式下（比如均匀分布、随机分布和高斯分布等）异构集群协同任务分配方式。