非Lévy型正交各向异性开口圆柱壳屈曲问题的辛叠加解析解
2024-01-05刘明峰倪卓凡李逸豪
刘明峰, 徐 典, 倪卓凡, 李逸豪, 李 锐
(大连理工大学 工程力学系 工业装备结构分析优化与CAE软件全国重点实验室, 辽宁 大连 116024)
0 引 言
圆柱壳以其轻质属性和优异的力学性能,被广泛应用于航空航天[1-2]、船舶工程[3]、土建工程[4]等领域,其结构失稳可能导致严重的安全问题,这使得屈曲分析成为圆柱壳结构设计中的必要环节.轴向载荷作用下的屈曲是圆柱壳最重要的失效模式之一,许多学者采用各类数值方法对其屈曲问题开展了深入研究,例如有限单元法[5]、有限差分法[6]、Galerkin方法[7-9]、Rayleigh-Ritz法[10]、微分求积法[11]、无网格法[12]等.
在数值方法兴盛的同时,对解析解的研究仍然具有重要意义:解析解不仅可以作为检验各种数值方法的对比基准,还能够快速揭示不同参量对结构力学行为的影响,从而指导结构的高效设计.然而,对于圆柱壳屈曲问题的解析解研究并不多见,例如:Zou和Foster[13]基于Flügge的各向同性圆柱壳线性理论,推导了轴压和外压共同作用下圆柱壳屈曲的一般解,并应用于正交各向异性圆柱壳的求解;张俊霖等[14]使用辛方法开展了吸湿老化影响下天然纤维增强圆柱壳的屈曲分析;桂夷斐和马建敏[15]根据Hamilton变分原理求解了弹性介质中受轴向冲击载荷作用的圆柱壳的屈曲;Sun等[16]发展了一种等效硬壳理论,用以预测准各向同性夹层圆柱壳的力学行为;Chen等[17]利用状态空间法分析了受压功能梯度弹性空心圆柱的分叉屈曲问题.已有研究大多聚焦封闭圆柱壳的屈曲分析,对于工程中亦常见的开口圆柱壳的屈曲问题则少有讨论,而板壳力学中的经典解析解法——Navier解法[18]和Lévy解法[19]又仅适用于四边简支和对边简支情况(即Lévy型开口圆柱壳),而对于非Lévy型情况则难以处理.
本文基于笔者近年来针对板壳力学问题提出的一种新解析方法:辛叠加方法[20-22],获得了经典解法难以直接求解的典型非Lévy型正交各向异性开口圆柱壳屈曲问题的解析解.该方法直接从正交各向异性圆柱壳的基本方程出发,将问题导入到Hamilton体系中,然后将非Lévy型边界下的原问题拆分为两个子问题,通过分离变量和辛本征展开求出子问题的解,进一步通过叠加求出原问题的解.在基于辛叠加方法的求解过程中,不需要预先选取试函数(如位移函数),而是通过逐步理性推导,严格得到问题的解,因而突破了半逆法的限制,可以求解传统框架下不易处理的壳体问题.通过数值算例验证了本文求解的正确性,并进一步开展了定量的参数分析,研究结果可以为开口圆柱壳的屈曲设计提供理论参考.
1 正交各向异性开口圆柱壳屈曲问题的控制方程
如图1所示,开口圆柱壳承受轴向力N1的作用,柱壳的厚度为δ,曲率半径为R,轴向(α方向)的弹性模量为E1、Poisson比为ν21,环向(β方向)的弹性模量为E2,Poisson比为ν12,剪切模量为G12.柱壳沿轴向、环向和径向的位移函数分别记为u,v和w.
1.1 基本方程
根据Kirchhoff-Love假设,壳体内部任意一点的应变分量可以表示为
e={eα,eβ,eαβ}T=ε+γχ,
(1)
其中ε={εα,εβ,εαβ}T={∂u/∂α,∂v/∂β+w/R,∂u/∂β+∂v/∂α}T,εα和εβ为中面内各点沿α和β方向的线应变,εαβ为面内切应变;γ为壳体中面法线方向的坐标;χ={χα,χβ,χαβ}T={-∂2w/∂α2,-∂2w/∂β2,-∂2w/∂α∂β}T,χα和χβ为中面内各点主曲率的改变,χαβ为扭率的改变.

图1 开口圆柱壳示意图Fig. 1 Schematic diagram of a cylindrical shell
对于正交各向异性圆柱壳,物理方程为
(2)
其中
b11=E1/(1-ν21ν12),b12=E1ν21/(1-ν21ν12),b22=E2/(1-ν21ν12),b66=G12.
进一步,基于Donnell薄壳理论[23],壳体所受内力和弯矩可以表示为
(3)
其中FT1和FT2分别为垂直于α和β轴的截面内单位宽度上的拉压力,FT12和FT21分别为相应截面内的平错力,M1和M2分别为弯矩,M12和M21分别为扭矩.
等效剪力V1,V2可以表示为
(4)
其中FS1和FS2分别为垂直于α和β轴的截面内的横向剪力.
壳体的平衡方程可以表示为
(5)
1.2 导入Hamilton体系
利用1.1小节所示基本方程,可将开口圆柱壳屈曲问题导入Hamilton体系.定义
(6)
由式(1)—(6)可以得到
(7)
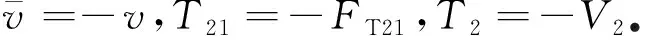
(8)
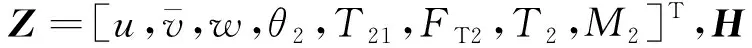
(9)
其中
(10)
采用类似的方法,定义∂w/∂α=θ1,对于子问题2,Hamilton对偶方程为
(11)

(12)
其中
(13)
这里
在辛几何求解框架下,可以采用分离变量[25]使得
Z=A(α)B(β),
(14)

(15)
其中μ为本征值,A(α)为本征向量.
式(15)中第二式的通解可以写为
(16)
其中λi是微分方程的特征值,待定系数Cji和Dji(j=1,2,…,8;i=1,2,3,4)并不相互独立.将式(16)代回到式(15)的第二式,可以得到系数之间的关系:
(17)
其中
2 非Lévy型正交各向异性开口圆柱壳屈曲问题的辛解析解
考虑如下边界条件的开口圆柱壳:
(18)
如图2(a)所示的原问题边界条件为:α=0和α=a边固支,用“C”表示,β=0和β=b边简支,但并不满足Lévy型边界条件[23],用“S′”表示.将原问题拆分成两个子问题:子问题1是四边简支的开口圆柱壳施加了非零的轴向位移u|β=0,b≠0,子问题2是四边简支的开口圆柱壳施加了非零的环向位移v|α=0,a≠0和弯矩M1|α=0,a≠0.两个子问题中的Lévy型简支边用“S”表示.
将式(16)代入α方向的对边简支边界条件,即
FT1|α=0,a=0,v|α=0,a=0,w|α=0,a=0,M1|α=0,a=0,
(19)
可以得到
sinh(aλ1)sinh(aλ2)sinh(aλ3)sinh(aλ4)=0.
(20)
求解μI-H的行列式展开可以得到重根零本征值μ00=0和本征值μim(i=1,2,…,8;m=1,2,3,…),对应的本征向量为
A00=[1,0,0,0,0,0,0,0]T,
(21)
A01=[0,0,0,0,b66δ,0,0,0]T,
(22)
以及
(23)
其中, 式(21)和式(22)分别由AA00=0和HA01=A00得到,am=mπ/a(m=1,2,3,…),uim,vim,wim,Kim分别为
(24)
齐次方程(8)的解可以写为
Z=[A00,A01,A11(α),A21(α),…,A81(α),…,A1m(α),A2m(α),…,A8m(α),…]B(β),
(25)
其中B(β)=[B00(β),B01(β),B11(β),B21(β),…,B81(β),…,B1m(β),B2m(β),…,B8m(β),…]T,由式(15)中的第一式可以得到
B01(β)=c01,B00(β)=c01β+c00,Bim(β)=cimeμimβ.
(26)
因此,子问题1的位移解可以写为
(27)
其中c00,c01和cim为待定系数.
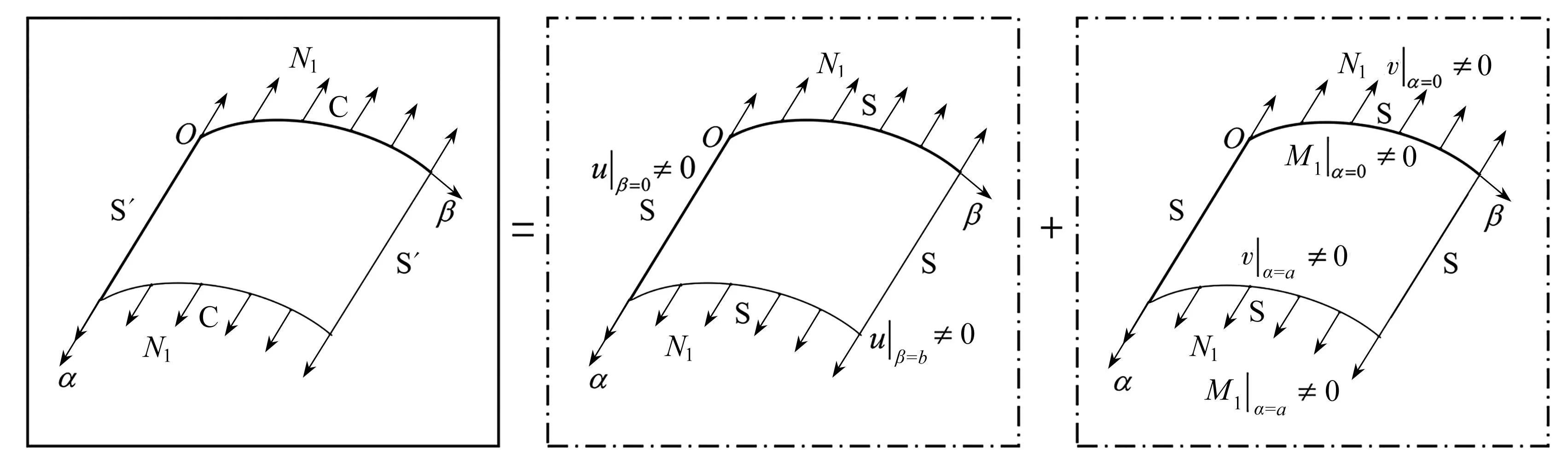
(a) 原问题 (b) 子问题1 (c) 子问题2 (a) The original problem (b) Subproblem 1 (c) Subproblem 2
在β=0和β=b处施加级数形式的位移,相关的边界条件可以表示为
(28)
将式(27)代入式(28),待定系数cim得以由u0m和ubm表示.
对于子问题2,代入相应的边界条件,同理可以得出位移解:
(29)
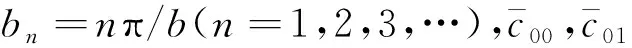
在α=0和α=a处施加级数形式的位移,相应的边界条件表示为
(30)
3 非Lévy型正交各向异性开口圆柱壳屈曲问题的辛叠加解析解
将式(27)和式(29)中两个子问题的解进行叠加,为了与式(18)所对应的原问题的解等价,还需要满足的边界条件为
(31)
将式(27)和式(29)代入式(31),利用三角级数展开,具体地,由FT12+(M12/R)|α=0=0可以得到
(32)
(33)
其中n=1,2,3,….
由FT12+(M12/R)|α=a=0可以得到式(32)和
(34)
其中n=1,2,3,….
由∂w/∂α|α=0,a=0可以得到
(35)
和
(36)
其中n=1,2,3,….
由FT21|β=0,b=0可以得到
(37)
(38)
以及
(39)
其中m=1,2,3,….
4 数 值 算 例
下面给出开口圆柱壳屈曲问题的数值算例.选取由石墨和环氧树脂组成的正交各向异性复合材料[26],其材料属性为E1=128 GPa,E2=11 GPa,ν12=0.25,G12=4.48 GPa.
表1为屈曲载荷解的收敛性研究,所研究的开口圆柱壳纵向尺寸与环向尺寸以及半径相同(a=b=R=1 m),δ分别为0.01 m和0.005 m.显然,在两种厚度下,所有计算结果在级数取20项时均收敛到5位有效数字(表中粗体数据),表明本文方法得到的解析解收敛性非常好.由于文献中缺乏可供对比的解析解,因此将本文的计算结果与有限元软件ABAQUS得到的结果进行对比,其中有限元的参数按照如下设置:采用S4R单元,网格大小为壳最小面内尺寸的1/100.表2和表3分别展示了不同尺寸下开口圆柱壳的屈曲载荷.当δ=0.01 m时,本文结果与有限元的差别均在5%以内;当δ=0.005 m时,与有限元的差别均在1%以内,验证了本文解析结果的正确性.除得到屈曲载荷之外,本文方法还得到了开口圆柱壳的屈曲模态,包括高阶模态.以a=b=R=1 m,δ=0.005 m的圆柱壳为例,图3给出了其前十阶屈曲模态与有限元结果的对比,结果高度吻合.
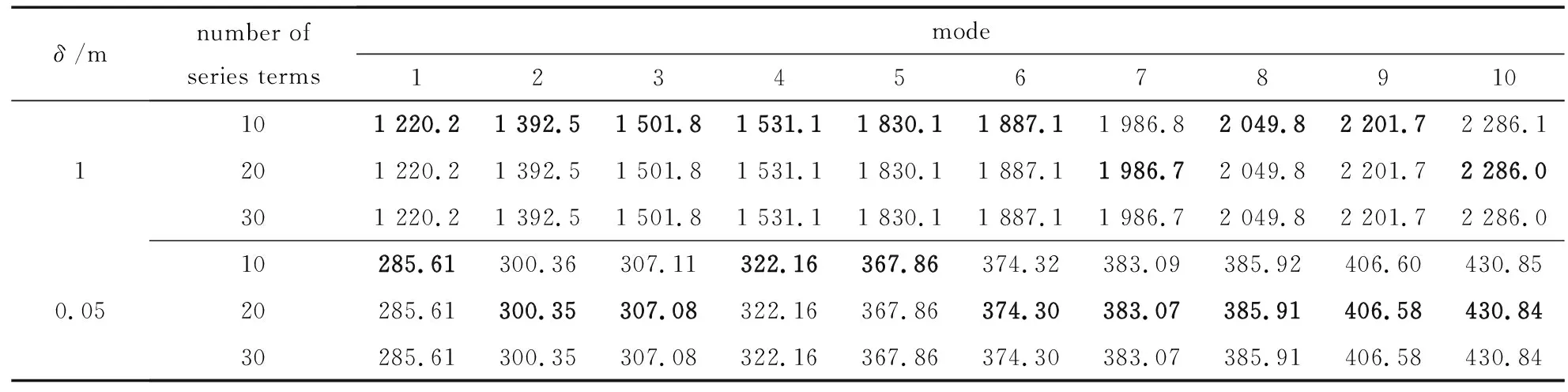
表1 a=b=R=1 m时,开口圆柱壳前十阶屈曲载荷的收敛性研究(单位: kN/m)
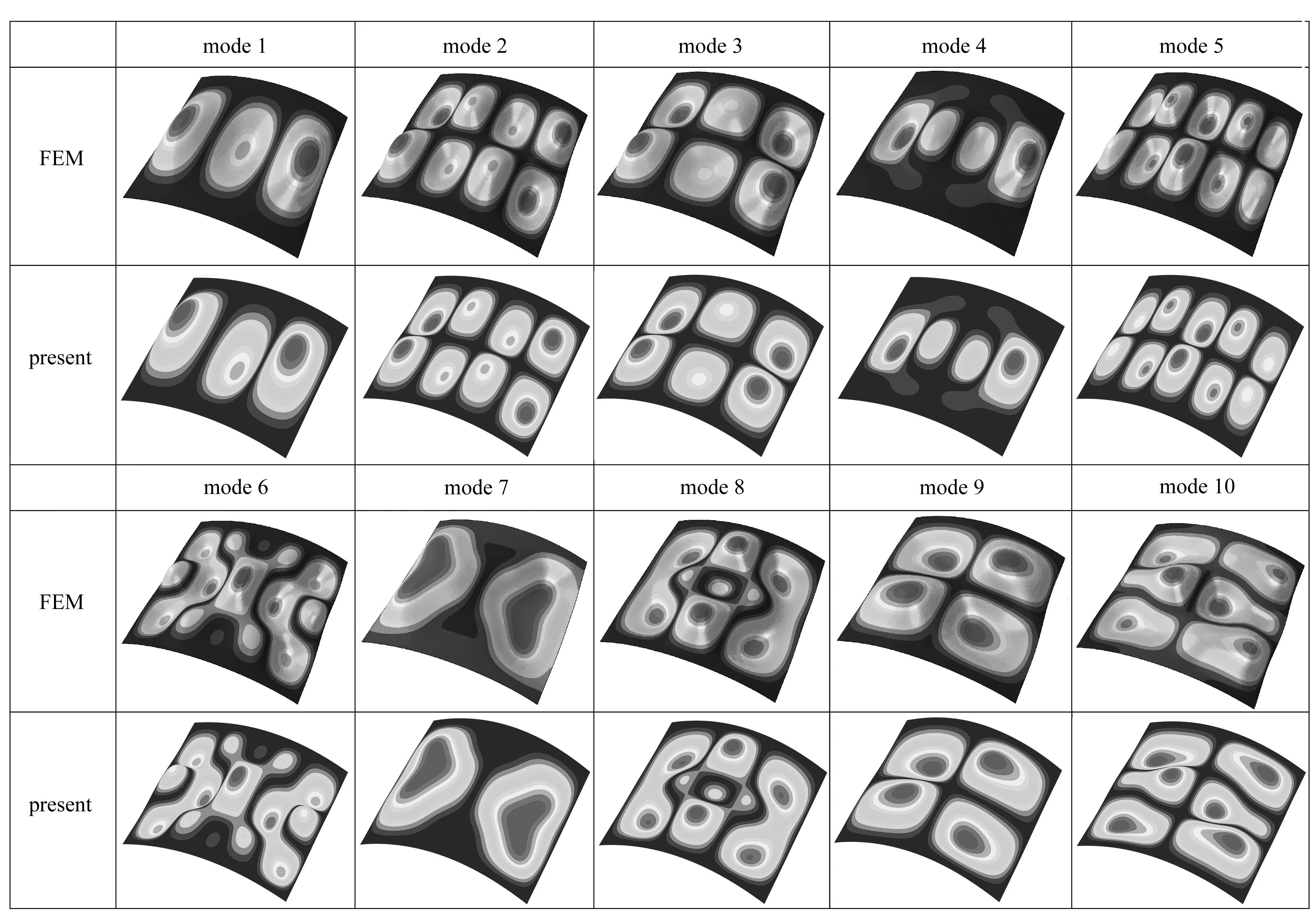
图3 开口圆柱壳的前十阶屈曲模态Fig. 3 The 1st 10 buckling modes of the cylindrical shell

表2 b=1 m, δ=0.01 m时,开口圆柱壳的前十阶屈曲载荷(单位: kN/m)
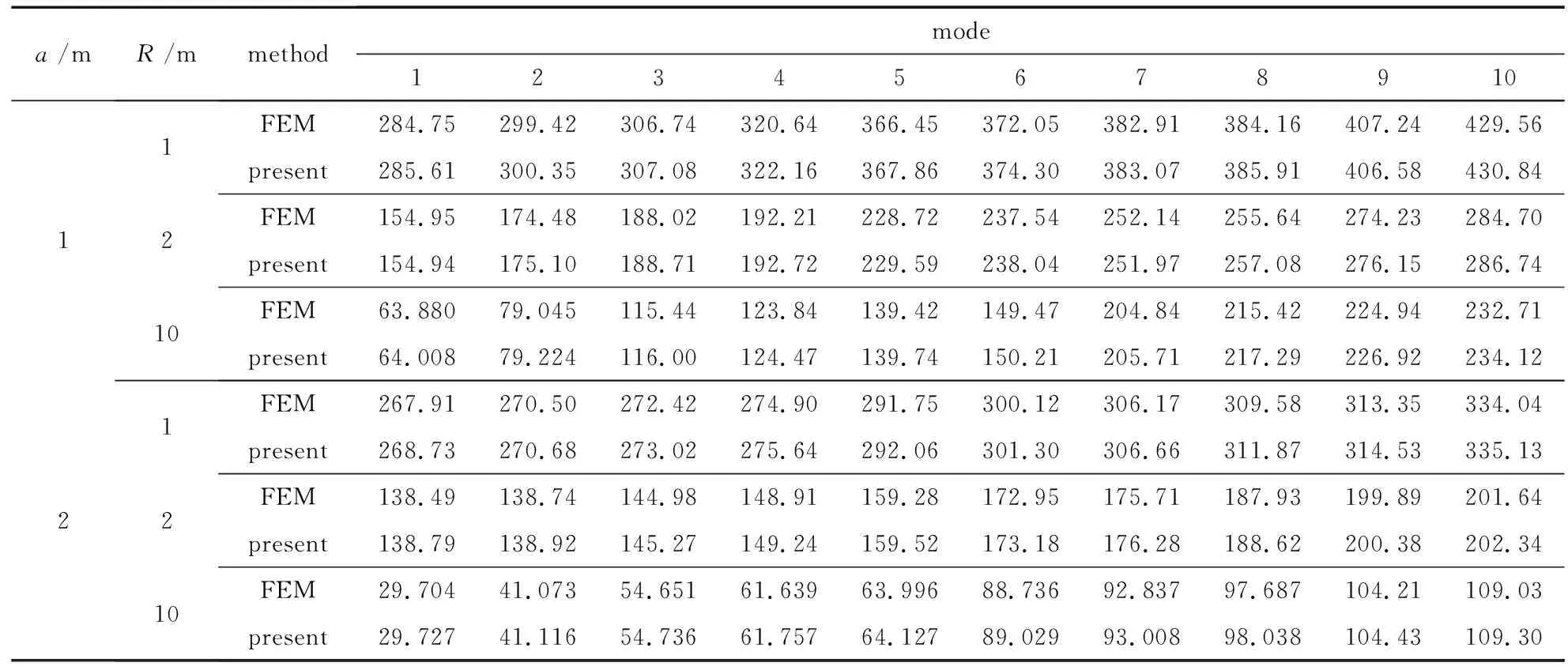
表3 b=1 m, δ=0.005 m时,开口圆柱壳的前十阶屈曲载荷(单位: kN/m)

图4 不同长度下,开口圆柱壳临界屈曲载荷随厚度的变化曲线
利用所得解析解进一步考查主要参数对开口圆柱壳屈曲结果的影响.图4给出了在不同长度下厚度对临界屈曲载荷的影响(取b=R=1 m).可以看到,随着厚度增加临界载荷均显著增大,而且在壳的长度较短时,这种效应更加明显.图5给出了两种厚度下曲率1/R对临界载荷的影响(取a=b=1 m),在曲率较小时,壳的形态接近于平板,随着曲率的增大,对轴向刚度的贡献加强,因而提高了壳的承载能力.上述结果可以为开口圆柱壳的抗屈曲设计提供参考.
5 结 论
由于高阶偏微分控制方程的求解困难,开口圆柱壳的解析求解本就是一项具有挑战性的课题,而对于非Lévy边界的正交各向异性开口圆柱壳的屈曲问题,求解难度无疑会进一步增加.本文从Donnell壳体理论的基本方程出发,导出了正交各向异性开口圆柱壳屈曲的Hamilton对偶方程,利用辛叠加方法,将原问题拆分,采用分离变量、辛本征展开求解得到子问题的解,最后根据叠加后的解与原问题解的等价性要求得到关于待定常数的齐次线性方程组,根据方程组有非零解的条件得到屈曲载荷解,进而得到相应的屈曲模态.由于文献中缺乏对应的解析解,因此采用有限元数值解对本文结果进行了对比验证,同时还利用本文的解研究了壳的尺寸对屈曲结果的影响.辛叠加方法在求解过程中无须假定试函数,兼备了辛方法的理性和叠加法的规律性,有望推广到更多壳体问题的求解当中.
