基于扭转-滑移耦合约束的梁桥抗倾覆滑移整体稳定分析

童上航, 肖汝诚, 庄冬利, 孙 斌

(同济大学 桥梁工程系, 上海 200092)

0 引 言

梁桥倾覆倒塌事故屡有发生,造成了严重的生命财产损失．车辆超载是引起梁桥倾覆的直接原因,据笔者不完全统计,近年来我国因车辆超载而倒塌的桥梁见表1,这些事故中的桥梁均为独柱墩连续梁桥,并且事故车辆都是靠边缘行驶导致倾覆扭矩过大,梁体发生滑移倾覆而落地．

为防止此类事故发生,众多学者致力于提高梁桥抗倾覆的整体稳定性能,并取得了一定成果．然而梁桥倾覆滑移机理尚未明确,计算方法仍不完善．目前梁桥倾覆计算方法主要分为刚体法、变形体法和精细化有限元法．刚体法将上部结构视为刚体,支座视为理想点支撑,选取荷载侧梁桥最外侧两支座的连线作为倾覆轴,验算抗力矩和倾覆力矩大小[1]．刚体法忽略了梁体变形和支座变形,会高估梁桥的抗倾覆能力[2]．变形体法认为梁桥会发生小变形,利用支反力验算抗倾覆能力．比如美国桥梁规范(AASHTO, 2007)通过控制最小支反力来保证不发生倾覆[3];国内交通运输部2018版新规范(JTG 3362—2018)将倾覆划分为两个特征状态,第一个状态控制支反力,第二个状态采用安全系数法[4]．彭卫兵等[5]基于变形体法提出了考虑支座尺寸影响的实用计算方法．然而,变形体法不能精确考虑梁桥大位移引起的几何非线性问题和支座与上部结构复杂相互作用引起的约束非线性问题．一些学者采取精细化有限元法模拟了倾覆过程[6-9],但精细化有限元建模复杂,计算成本高,不适合工程应用．可见上述三种计算方法各有不足,因此,建立一种兼顾分析精度和计算效率的改进方法显得尤为重要．

一些学者已尝试建立改进方法来计算部分支座失效后梁桥的平衡状态,例如Shi等[10]将等效惯性矩应用于Euler-Bernoulli梁并假定支座不发生滑移,建立了一种简化模型去分析梁体与支座脱空后的平衡状态．事实上,支座滑移是梁桥整体失稳破坏的控制条件之一,并且支座摩擦因数直接关系到主梁的抗滑移能力[11-13]．由此可知,建立改进方法应明确支座与上部结构的相互作用机理,着重考虑支座脱空滑移对梁桥整体失稳的影响．鉴于此,本文提出了一种基于曲梁单元考虑扭转-滑移耦合约束的梁桥整体稳定性分析方法,该方法可计算各种支座失效情况下的梁桥平衡状态,并准确判断梁桥整体失稳模式．具体来说,本文工作如下:推导了七自由度曲梁单元刚度矩阵,建立了各种支座失效情况下的支座约束方程,并将支座约束方程引入有限元总方程参与求解．将梁桥整体失稳分为倾覆和滑移两种情况,提出了以各支座受力状态判断梁桥整体是否失稳的计算流程,并编制了相应的计算程序．以简支超静定曲梁为例,对比解析解、ANSYS中含翘曲自由度的Beam 188单元计算结果和本文所提出七自由度曲梁单元的计算结果,检验了本文所提出曲梁单元的精度．利用所提出方法评估了某匝道桥事故案例,分析了在不同荷载放大率下的支反力大小变化及支座失效情况,还原了失稳发展历程．通过对比本文所提出方法和传统杆系有限元模型的支反力结果,验证了本文方法能更精确地模拟各种支座失效情况下的梁桥平衡状态．

1 曲梁单元刚度矩阵

文献[14]推导了包含竖向挠度和扭转角的曲梁单元刚度矩阵,本文所提出的支座约束方程中包含梁的横向位移,而曲梁纵向位移与横向位移的刚度是相互耦合的．因此本文在文献[14]的基础上引入横向位移和纵向位移,推导了七自由度曲梁单元刚度矩阵．

在曲梁的剪切中心轴线上建立直角流动坐标系,其中z轴沿轴线切线方向,x轴指向轴线曲率中心,y轴垂直xOz平面向下．u,v,w分别为x,y,z方向的位移,φ为截面扭转角．截面内力分量和流动坐标系如图1所示．设梁的截面面积为A,弹性模量为E,剪切模量为G,绕x轴的惯性矩为Ix,绕y轴的惯性矩为Iy,扭转惯性矩为Id,扇形惯性矩为Iω．

图1 曲梁截面内力分量与流动坐标系Fig. 1 The internal force components and the co-rotational coordinate system of the curved beam

曲梁单元一个结点有七个自由度,包括纵向位移w、横向位移u及其导数u′(对纵坐标z的导数)、竖向位移v及其导数v′、扭转角φ及其导数φ′．设单元长度为2λ,曲率半径为R,如图2所示．

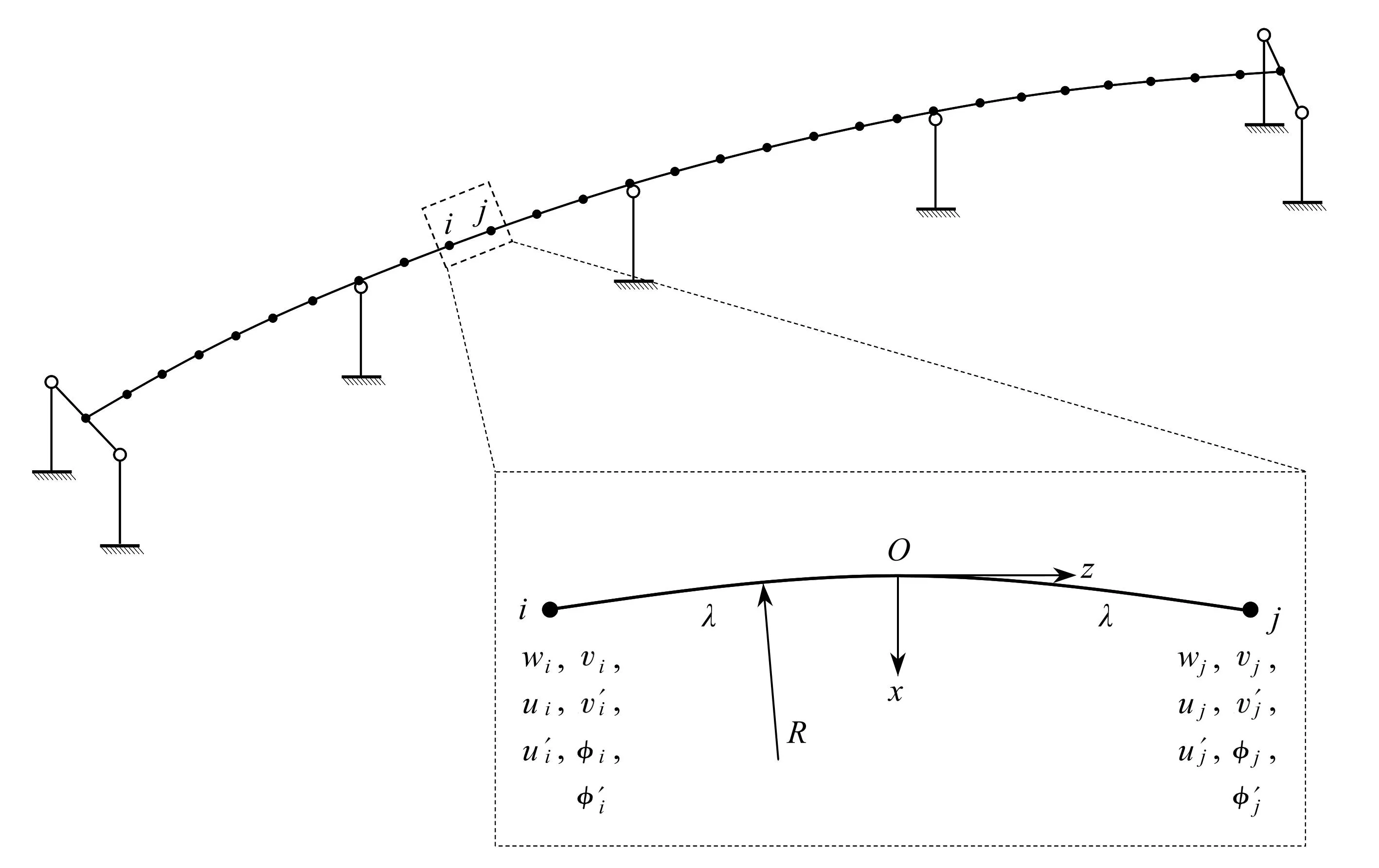
图2 七自由度曲梁单元Fig. 2 The curved beam element with 7 degrees of freedom

令自然坐标ξ=z/λ,纵向位移w采用线性位移模式,横向位移u、竖向位移v和扭转角φ都采用三次位移模式:

(1)

以上位移模式结合结点位移δi=[wiuiu′iviv′iφiφ′i]T和δj=[wjuju′jvjv′jφjφ′j]T,可解得a0,a1,b0,b1,b2,b3,c0,c1,c2,c3,d0,d1,d2,d3等系数．将这些系数代回方程(1),可推导出单元形函数矩阵N:

(2)

其中形函数

曲梁的几何方程、截面内力与变形的关系如下[14-16]:

(3)

(4)

其中N为截面轴力,My和Mx分别是沿y方向和沿x方向的弯矩,Td为自由扭转矩,Tω为约束扭转矩,B为双力矩．将式(2)、(3)代入式(4),解得广义应力与结点位移δ的关系:

[NMyMxTdBTω]T=DBδ,

(5)

其中弹性矩阵D为

广义应变矩阵B为

B=

其中N′1表示N1对z求导．

由虚功原理和变分原理可解得曲梁单元刚度矩阵为

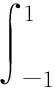
(6)

当曲梁单元的半径趋于无穷大时,其单元刚度矩阵便退化为直梁的单元刚度矩阵．

记外力集中荷载为F=[PxPyPzMxMyMz]T,分布荷载为f=[qxqyqzmxmymz]T,所有外力荷载分量的正方向与流动坐标系正方向一致,可得单元结点荷载为

(7)

其中

N′3表示N3对z求导．

2 支座约束方程与梁桥失稳判断

当忽略支座尺寸对梁桥倾覆的影响时,支座视为一个点支撑上部结构:对于单支座墩,其失效模式可分为脱空和滑移;对于双支座墩,其失效模式可分为单侧脱空不滑移、单侧脱空且滑移和双支座都脱空．本文提出的迭代求解思路是先计算所有支座未失效情况下的有限元解,然后检查每个支座处的支反力和扭转角．如果支反力受拉,则支座脱空,去除该支座;如果扭转角大于摩擦角,则支座发生滑移,应引入扭转-滑移耦合约束方程．然后求解改变支座约束条件后的有限元总方程．

2.1 支座约束

2.1.1 支座未脱空且未滑移

对于单支座墩,梁桥横向位移和竖向位移都被支座限制,因此约束条件为

(8)

而对于双支座墩,不仅约束横向位移和竖向位移,还会约束梁的扭转以及曲梁平面内弯曲,即

(9)

2.1.2 单墩支座脱空和双支座墩完全脱空

支座未脱空未滑移时,为实现约束方程(8)、(9),可采用对角元素改1法[17],并将结点载荷列阵相应元素改为0．支座仅承压,如果支座支反力计算结果为受拉,说明支座发生脱空,应去除该位置的支座约束条件．直接在总刚度矩阵和结点载荷列阵中还原相应的元素即可．

2.1.3 需要引入约束方程的支座失效情况

需引入约束方程的失效情况包括单墩支座滑移、双支座墩单侧脱空不滑移和双支座墩单侧脱空且滑移．以单墩支座发生滑移为例,当梁桥在单墩支座结点处的扭转角大于摩擦角时,梁桥在该支座处会发生滑移．设支座给梁桥底面法向力为N,摩擦力为f,忽略摩擦力在纵桥向的分量,摩擦因数为μ,梁桥截面剪心到底面的距离为hb,剪心OSC在截面内的位移r=(u,v)．为方便在有限元求解方程中引入扭转-滑移耦合约束,规定Px为支座反力沿x方向的分量,Py为沿y方向的分量,mz为支座反力给发生位移后剪心位置的扭矩,Px,Py和mz将作为待求量参与有限元总方程求解,如图3所示．

① 扭转角大于0(即与流动坐标系正方向一致)

梁桥在支座处结点的横向位移u,竖向位移v,扭转角φ满足几何约束条件为

g1=utanφ-v+hb(1-secφ)=0,

(10)

支反力给剪心的扭矩为

mz=Px(v-hb)-Pyu,

(11)

因此第二个约束方程为

g2=-mz+Px(v-hb)-Pyu=0．

(12)

摩擦力f和法向力N满足

(13)

由此可得第三个约束方程为

g3=Py(sinφ-μcosφ)+Px(cosφ+μsinφ)=0．

(14)

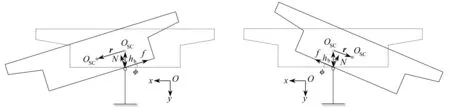
(a) φ>0 (b) φ<0

② 扭转角小于0

同理可得三个约束方程为

(15)

对于其他需要引入约束方程的支座失效情况,其推导过程与单支座墩滑移类似．所有的约束方程汇总见表2．

表2 支座约束方程

2.2 梁桥失稳判断

在求解过程中,先计算所有支座都有效的位移解,根据支反力正负和扭转角大小判断各支座是否失效(脱空或滑移),然后改变各支座约束条件,在有限元求解总方程中引入支座约束方程重新求解,再检查各支座的失效模式,如果失效模式发生改变则修改约束方程,则再次重新求解,直至各支座失效模式不改变为止．最后根据各支座的失效情况判断梁桥是否失稳(整个上部结构滑移或倾覆)．

2.2.1 利用Newton-Raphson迭代法求解含约束条件的有限元方程

对于支座未滑移未脱空、单支座脱空和双支座完全脱空这三种支座失效模式,只需修改总刚度矩阵和结点载荷列阵即可．而对于单支座滑移、双支座单侧脱空不滑移和双支座单侧脱空且滑移,则需要引入约束方程,支反力Px,Py和支反力对剪心扭矩mz将作为待求量引入结点位移列阵共同参与求解．当有k个支座需要引入约束方程时,有限元求解总方程为

(16)

其中

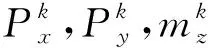
利用Newton-Raphson迭代法求解方程(16),即迭代求解

a(k)=a(k-1)-J-1(a(k-1))F(a(k-1)),

(17)

直至增量小于精度ε:

‖J-1(a)F(a)‖<ε,

(18)

其中J(a)为F(a)的Jacobi矩阵,

2.2.2 梁桥失稳判断方法

上部结构可能发生的失稳模式有滑移和倾覆．当所有支座都发生了脱空或滑移时,上部结构将发生整体滑移．如果没发生整体滑移,但承压支座仅剩一个或两个,那么上部结构将发生倾覆．实际工程中支座的容许扭转角较小,摩擦角较小,滑移往往会先于倾覆发生．

综上所述,梁桥失稳判断流程为:

我国体育教师教育培训主要由职前教育系统和在职培训系统两大系统组成。体育专业院校和师范院校的体育院系主要承担体育教师的职前教育，各级各类的教育学院和教师进修学校主要承担体育教师的在职培训。目前，我国高校中体育教师的培养还存在着诸多问题，其中“训练”比“教育”重要的思想使得体育教师职前教育的课程体系缺乏“师范性”。而体育教师正要通过体育教育学类的课程来学习、掌握和运用来实现其专业的垄断性和不可替代性。因此，建立和完善体育教育学科的课程体系是提高体育教师教育质量、保障体育教师专业地位的重要条件。

1) 假定所有支座有效,求解第一次有限元方程

Kδ=P．

2) 根据各支座的扭转角和支反力判断各支座的失效模式．对于单支座墩,如果支反力受拉,则支座脱空;如果支反力受压但扭转角大于摩擦角,则支座发生滑移．对于双支座墩,如果两个支座的支反力都受拉,则两个支座都脱空;如果只有一个支座受压,则是单侧支座脱空,然后根据扭转角是否大于摩擦角判断是否发生滑移．

3) 如果所有支座都发生脱空或滑移,则上部结构发生滑移,退出计算．

4) 如果承压的支座只剩一个或两个,则上部结构发生倾覆,退出计算．

5) 如果上部结构未发生滑移或倾覆,则判断与上一次求解相比支座失效模式是否发生改变:如果未发生改变则退出计算,梁桥未发生整体失稳;反之则根据支座失效模式修改支座约束方程G和总刚矩阵Keq,利用Newton-Raphson迭代法求解有限元方程

然后返回步骤2)．

3 算 例 分 析

3.1 简支超静定曲梁分析

为检验曲梁单元的精度,以简支超静定曲梁为例,对比理论解析解、ANSYS中含翘曲自由度的Beam 188单元计算结果和七自由度曲梁单元计算结果．在均布竖向荷载和均布扭矩作用下,简支超静定曲梁的扭转角φ和竖向挠度v解析解为[14]

(19)

表3 各参数取值

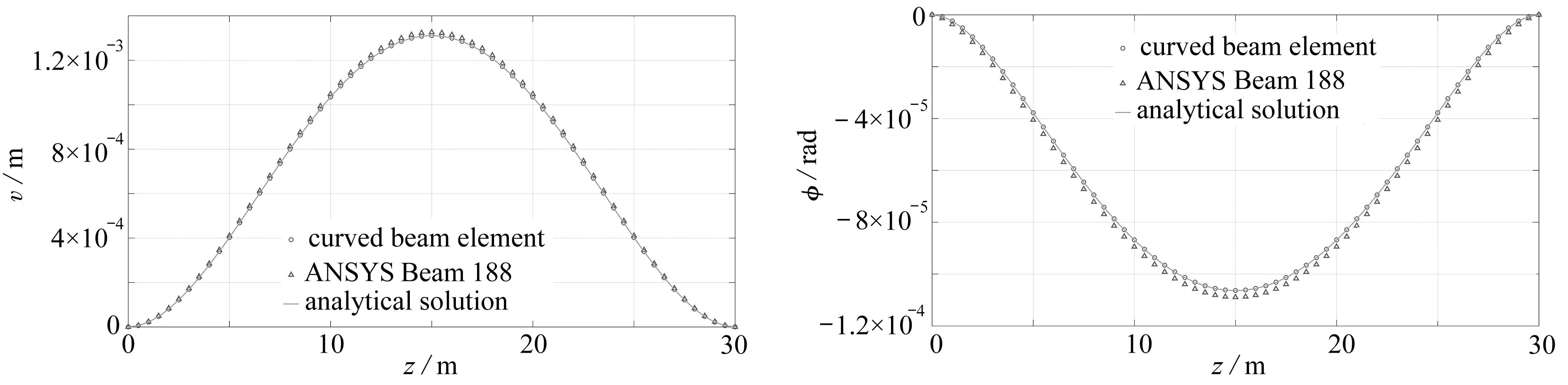
图4 挠度的理论结果与有限元结果比较

3.2 某匝道桥事故分析

某匝道桥发生倒塌,事故发生时有3辆重约110 t的货车行驶在曲梁靠外侧(近倾覆侧),1辆较轻的车在靠内侧(计算中忽略)．倒塌曲梁段长75 m,曲线半径220 m,平面布置和箱梁横断面如图6、7所示．单墩支座摩擦因数取0.3[18],联端双支座摩擦因数取0.01,主梁材料为C50混凝土．

图6 平面布置图(单位: m)

定义荷载放大率为施加汽车荷载的比例系数．车辆荷载的荷载放大率从0.1开始逐渐增大,计算所有支座的竖向支反力,如图8所示．当荷载放大率为0.45时,联端内侧支座P1-2和P4-2发生脱空;放大率为0.55时,联端外侧支座P1-1和P4-1发生滑移;放大率达到0.93时,箱梁最大扭转角16.8°,已超过单墩支座摩擦角,单墩支座P2和P3发生滑移,此时所有未脱空支座都发生滑移,箱梁在支座处受到的水平力指向外侧,箱梁整体往外侧滑移,还没有达到事故车辆荷载大小就已经倒塌．因此,在事故车辆荷载作用下,联端内侧支座发生了脱空,并且其他所有支座发生了滑移,箱梁整体发生滑移然后沿P2和P3连线倾覆,扭转角发散．由式(15)第三个约束方程可知,墩柱顶受到的水平力会随着扭转角发散急剧增大,墩柱底弯矩过大发生强度破坏,事故现场P2和P3墩柱也确实发生墩底破坏而倒塌[8]．

图8 不同荷载放大率下各支座的竖向支反力Fig. 8 The vertical support reaction of each bearing under different load amplification ratios

规范方法基于传统的杆系模型验算抗倾覆能力[4],但传统杆系模型假定所有支座有效,不能模拟上部结构与支座的复杂相互作用,而本文所提出的方法可以模拟支座脱空和支座滑移带来的影响．根据图8,选取荷载放大率为0.1,0.5和0.8三种工况,分别对应所有支座有效、联端内侧支座脱空和联端外侧支座滑移三种情况,对比本文方法和传统模型的竖向支反力计算结果,如图9所示．在0.1倍车载作用下,两者的竖向支反力最大相差2.80%;在0.5倍车载作用下,本文方法判断出联端内侧支座P1-2和P4-2发生脱空,支反力为0,而传统模型算得支座P1-2和P4-2承受拉力;在0.8倍车载作用下,本文方法结果中的各支反力与传统模型相比都有显著差异,可见支座脱空滑移对支反力影响较大．传统模型不能准确计算上部结构与支座的相互作用,无法模拟实际事故中支座脱空和支座摩擦滑移的现象,而本文提出的模型克服了其不足之处,能够更精确地模拟各种支座失效情况下的梁桥平衡状态．从计算效率来看,以0.1倍车载工况为例,本文方法计算耗时0.11 s(采用MATLAB计算),传统杆系模型耗时0.52 s(采用MIDAS/Civil计算),可以预计本文方法对于更复杂的梁桥结构具有更高的计算效率．

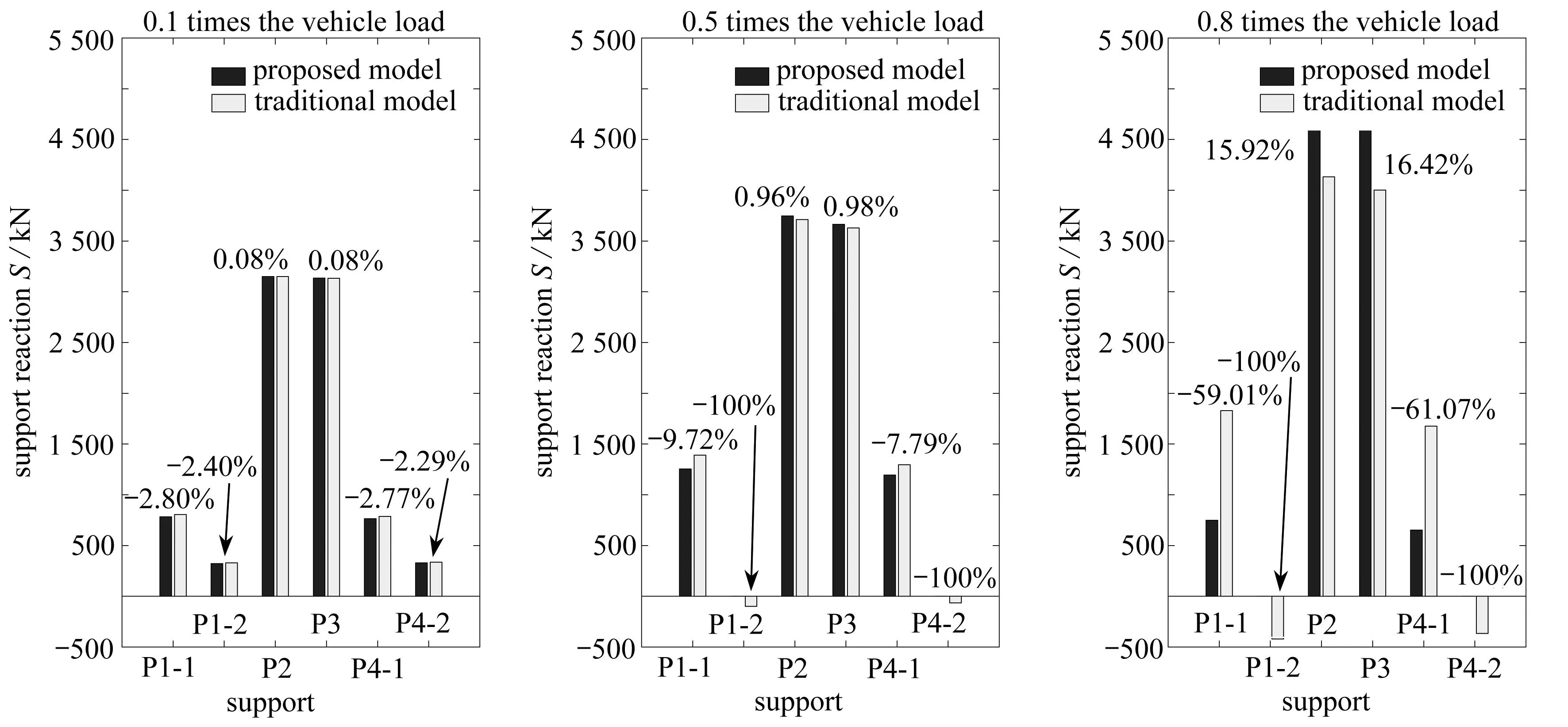
图9 所提出计算模型与传统模型的竖向支反力对比Fig. 9 Comparison of the vertical support reactions given by the proposed model with the traditional model

4 结 论

1) 本文对比了简支超静定曲梁的解析解、Beam 188单元有限元解和本文所提出七自由度曲梁单元的有限元解．从位移的计算结果来看,本文所提出的曲梁单元比Beam 188单元更接近解析解,验证了曲梁单元的高精度性．

2) 本文分析了某匝道桥倒塌事故．在不同荷载放大率条件下通过计算各支座的支反力大小和判断各支座失效情况,还原了该匝道桥失稳发展历程:在事故车辆荷载作用下,联端内侧支座脱空,其他所有支座发生滑移,因此该梁桥先发生滑移然后倾覆落地．通过对比分析本文方法与传统杆系有限元模型在所有支座有效、联端内侧支座脱空和联端外侧支座滑移三种情况下的计算结果,验证了本文方法能更精确地模拟各种支座失效情况下的梁桥平衡状态．