基于遗传算法的超声电火花微小孔加工用柔性铰链的数值分析与优化
2024-01-05刘晋丽
刘晋丽
(西安航空职业技术学院,陕西西安 710089)
0 引 言
微小孔在航天航空、医疗器械、发动机、芯片制造设备等尖端精密零件与设备中广泛存在,并且通常是影响设备精度的关键[1]。由于微小孔孔径较小,长径比较大,因此对加工工艺的要求更为严格。目前,微小孔的加工方法多达50余种,其中机械加工与特种加工是主要的加工方式[2]。机械加工受加工刀具的限制较大,并且排屑困难。特种加工的微小孔粗糙度较大,加工效率低。近些年,将超声加工与电火花加工复合的微小孔加工方式得到认可。
超声电火花(EDM)加工是在电火花加工的基础上使用超声进行辅助,电极在超声振动的作用下,可以将烧蚀产生的废渣快速排出,从而提高加工速度和精度。中北大学的马靖、李瑞宣等人分别从电极形状、切削液影响等方面进行研究,加工精度得到有效提升[3-4]。天津大学的倪皓[5]则对超声电火花加工的机理进行深入的研究,并对核心部件进行优化设计分析。SRIVASTAVA等[6]创新性地提出将液氮引入加工过程中,从而降低电极的损耗。SHABGARD等[7]则对电极的超声振动参数进行研究,以确定其对加工效率和精度的影响。但是,以上研究忽视了电极在超声振动过程中的横向振动,这会引起电极出现扰动从而增加圆度误差。
本文将柔性铰链结构用于降低电极的横向振动。首先对柔性铰链的结构参数进行选择,分析柔性铰链在加工过程中的受力,并通过遗传算法选择最佳的柔性铰链参数。然后,对比在增加柔性铰链后的电极进行模态分析与谐响应分析。结果表明,通过遗传算法得到的柔性铰链可以有效降低电极的横向振动,从而优化微小孔的轮廓。
1 基于遗传算法的柔性铰链设计
超声辅助电火花加工可以改善传统电火花加工微小孔过程中产生的电蚀产物在孔底堆积的问题,其加工原理如图1(a)所示,为了抑制电极在加工过程中受力产生的扰动,在中间位置增加图1(b)所示的柔性铰链。

(a) 超声电火花加工微小孔装置
1.1 柔性铰链受力分析
柔性铰链可以利用自身的形变完成运动或力与能量的传导,它具有高精度、简易、阻力小等优势。通过柔性铰链的结构设计,可以实现对物体的运动幅度放大或者缩小。这对于微小孔加工等精密加工具有很大的帮助。常见的柔性铰链有直圆形、直梁形、椭圆形等三种形式,根据之前的研究,直圆形柔性铰链的刚度最大,变形量较小,因此适用于振动抑制[8]。又因为双直圆形结构具有更大的力传导效果,因此本设计中柔性铰链为双直圆形结构。图2为双直圆形柔性铰链的受力分析图。

图2 柔性铰链受力分析Fig.2 Force analysis of flexible hinges
超声电火花设备在工作过程中,电极在超声波发生器的作用下,进行轴向的往复运动。但是在振动过程中,电极受到待加工工件的阻力会产生横向的力,即产生扰动现象。为了提高加工精度和效率,应当在提升轴向力的同时避免其他方向的力产生。
在轴向振动与横向振动的共同作用下,柔性铰链会受到3个方向的力,分别是柔性铰链x方向的法向力Fx,y方向的切向力Fy,z方向的切向力Fz以及扭矩My。在这3种力的作用下,柔性铰链分别产生对应的形变,分别是由Fx引起的x方向的变形Δx,Fz引起的z方向的形变Δz以及角变形αz,Fy和My共同作用下导致的y方向的线性变形Δy和角变形αy。
由文献[9]可知,影响柔性铰链的主要结构参数是圆半径R,铰链梁宽b,x方向上的两圆距离l,以及铰链厚度h。通过柔度值αy/My、αy/Fy、 Δz/My和Δz/Fz可以表示电极轴向运动的效果,而αz/Mz、αz/Fy、 Δy/Mz、 Δy/Fy、 Δx/Fy可以描述横向振动的影响。
1.2 利用遗传算法优化柔性铰链结构
遗传算法是一种模拟自然生物优胜劣汰进化过程的优化算法,具有较高的优化效率[10]。在本文中,影响柔性铰链的主要参数为R,b,l和h,因此柔性铰链的设计变量共有4个。
而评价柔性铰链效果的指标是柔度值,若在电极轴向上获得较大的振动同时抑制横向振动,就需要轴向的柔度值尽可能大而横向的柔度值尽可能小。轴向上的柔度评价函数为:
(1)
横向上的柔度评价函数为:
(2)
由文献[11]可知,

(3)

(4)
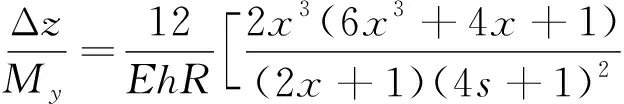
(5)
(6)
(7)
(8)
(9)

(10)
(11)
式中,x=R/t。E为弹性模量。
将式(3)~(11)分别带入式(1)和(2)中,定义f(x)=S2∶S1为柔性铰链的s适应度函数,当f(x)的值越小,柔性铰链的横向减震效果最佳。在对超声电火花加工电极的柔性铰链进行设计时,需要结合电极尺寸设置柔性铰链的参数范围。因此对主要参数进行如下的约束:
(12)
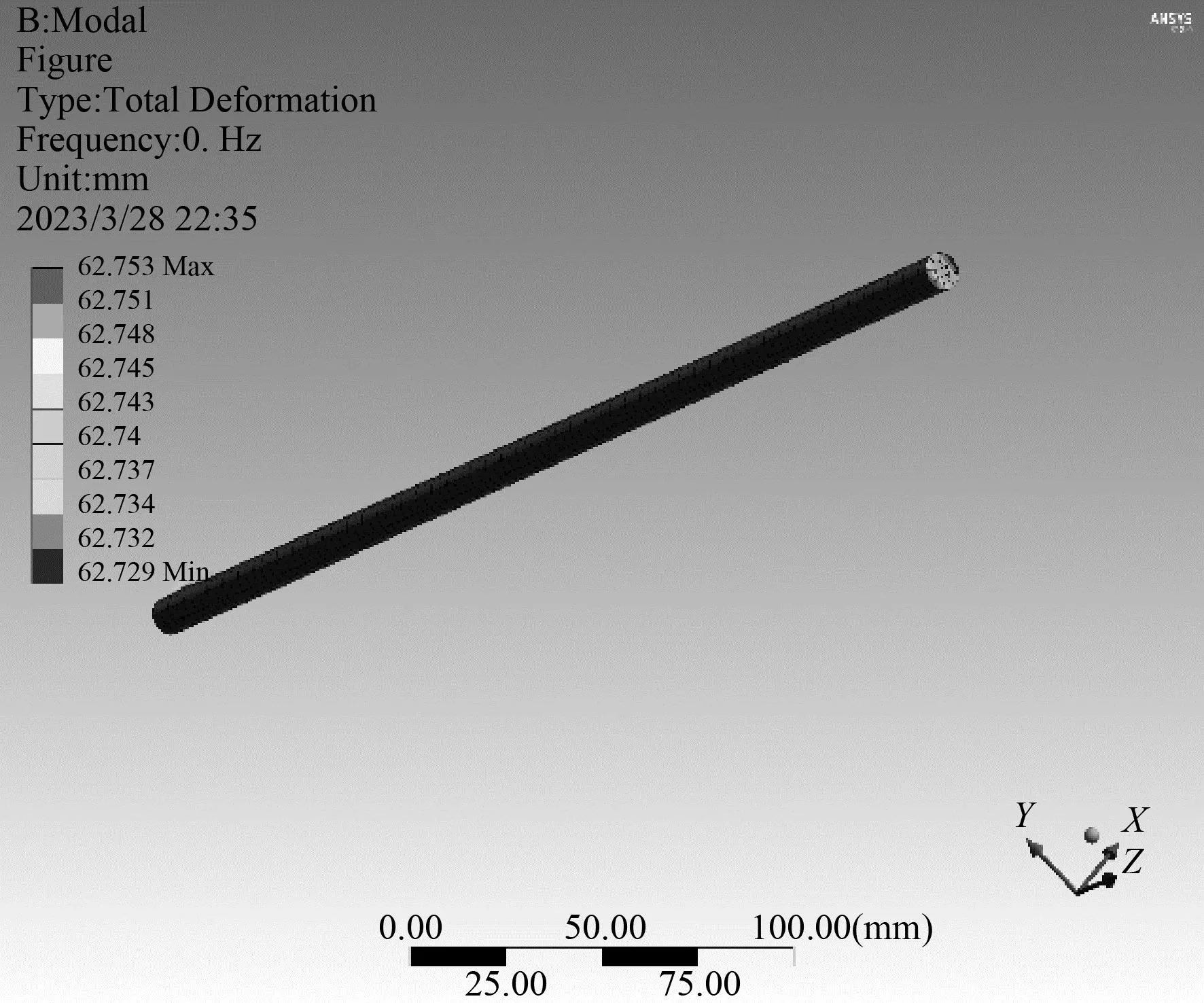
1.2 1.25 利用Matlab中的遗传算法工具箱进行参数优化。将约束条件和适应度函数输入Matlab中。其中,柔性铰链的材料设为304不锈钢,其弹性模量为200GPa。在如图3所示的113次迭代后,得到了柔性机构的最佳尺寸(表1)。 表1 柔性铰链最佳参数组合Tab.1 Optimal parameter combination of flexible hinges 表2 固有频率Tab.2 Natural frequencies Hz 图3 优化迭代过程Fig.3 Optimization iteration process 根据之前的优化,得到了柔性铰链的优化结构参数。针对此结构进行有限元分析,比较柔性铰链对电极振动产生的影响。 首先比较了有无柔性铰链情况下的模态。图4是电极在有无柔性铰链情况下的模态。通过对比前6阶模态,可以看出,在无柔性铰链的情况下,电极的共振频率较小,而在加入柔性铰链之后,电极的轴向频率得到很大提升,并接近于实际加工中设置的超声频率(1kHz)。 (a) 无柔性铰链时电极的一阶模态 并通过对比电极(图5)的横向振动,可以看出在低频区域,柔性铰链作用下的电极横向频率在一阶时最大,且大于无铰链的情况;而在高频区域,柔性铰链作用下的电极横向振动幅值趋近于0,远小于无铰链的情况。由于电极的工作频率在1kHz左右,因此通过本文设计的柔性铰链可以有效抑制横向振动的发生。 图5 有无柔性铰链作用下电极的横向振动幅值Fig.5 Lateral vibration amplitude of the electrode with and without flexible hinges 进一步,通过参数研究,验证经过遗传算法优化后的柔性铰链的效果。由于柔性铰链的效果是多种结构参数共同影响的,因此,使用正交法进行参数选择。正交实验法是研究多因素多水平的一种设计方法,它依据Galois理论从全面实验中挑选出部分具代表性的水平组合进行实验,并对结果进行分析,从而找出最优的水平组合[12]。参数选择范围即式(12)的约束范围,使用4因子3水平的L9(34)设置。正交表如表3所示。 表3 仿真试验正交表Tab.3 Orthogonal table for simulation test 通过仿真对比正交表中参数的柔性铰链在第5阶和第6阶的横向振动和轴向振动,可以得到出在工作频率下柔性铰链的工作效率。如图6所示,试验1~9分别对应表3中的柔性铰链参数,试验10则为经过遗传算法优化后的结构。在第5阶和第6阶时,经过优化后的柔性铰链结构均有最好的横向振动抑制效果,同时,轴向振动幅值也最大。因此,验证了遗传算法优化的可行性。 (a) 横向振动幅值 本文设计了一种双直圆柔性铰链结构,以抑制电极的横向振动,同时放大轴向振动。首先,建立了柔性铰链在电极工作时的受力模型,并得出影响柔性铰链效果的主要参数。其次,通过遗传算法对结构进行参数优化,确定最佳的结构参数。最后,通过有限元分析的方法对柔性铰链与电极组成的系统进行模态分析。通过对比分析可以得出,柔性铰链可以在放大轴向振动的前提下抑制横向振动,此外,经过遗传算法优化的结构具有最好的效果。


2 电极的模态分析



3 结 论
