基于第一性原理计算的高熵合金研究现状

欧阳文恒,周佳宇,蒋德宇,李 勇,刘畅熙,王立强

(1. 海军装备部,江西 九江 332005;2. 上海交通大学 材料学院与工程学院 金属基复合材料国家重点实验室,上海 200240;3. 天津航海仪器研究所九江分部,天津 300131)

0 引 言

高熵合金(HEAs)具有高强度、良好延展性、高硬度和良好的耐腐蚀性等优点,在诸多领域引起了广泛关注[1-2]。高熵合金为多种主要元素以相似比例组成的合金,单个原始的占比范围为5%～35%。因此,高熵合金与传统合金有所不同,其具有一些特殊的效应、即高熵效应、缓慢扩散效应、强晶格畸变效应和鸡尾酒效应[3-4]。高熵合金具有高强度、大延展性、抗腐蚀和高硬度等优异的综合性能,因此在工业、航空航天、海洋等领域具有巨大的应用潜力[5-7]。

然而目前关于高熵合金的研究主要集中在工艺性能的提升等方面,一般采用成分设计方法,费时费力[8-9]。因此,如何更加简便、快速发现高强度、高硬度和抗腐蚀性好,综合性能良好的高熵合金是一项具有挑战性的课题。目前,随着对高熵合金设计的深入研究,已有诸多研究人员总结归纳出一些设计理论[10-11]。近年来,有许多课题组对第一性原理计算模拟在材料设计的应用进行了研究[12-15]。

因此,本文针对第一性原理计算模拟在高熵合金开发中的应用研究进展进行综述,总结了第一性原理计算的理论及应用,并对其未来的研究发展做出展望,为开发设计新型高熵合金提供参考。

1 第一性原理计算简介

第一性原理计算通过电子相关参数求解体系性能,在过去的几十年里,第一性原理计算不断取得重要的理论和算法进步[16]。与此同时,计算机技术也在迅速发展,正是这些进步使人们能够解决具有实际意义的问题[17]。由于每个电子的运动都对应着各自的薛定谔方程,这需要求解复杂的薛定谔方程组,必须进行近似求解[18]。

1.1 薛定谔方程及其近似

多电子体系薛定谔方程[19-21]如下:

(1)

(2)

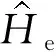
由于材料体系所含粒子数量十分庞大,求解计算复杂,可以近似简化为只有电子运动的体系,即绝热近似(adiabatic approximation)[22]。

1.2 密度泛函理论

在多电子体系近似的基础上,进一步有单电子近似模型及Hartree-Fock方程[23]。最终,由Hohenberg和Kohn奠定密度泛函理论(DFT)的基础[24]。密度泛函理论能够有效地计算模拟体系电子与能量的变化[25]。

根据Hohenberg-Kohn定理,在给定的外部势场中,求解体系内部能量泛函F[ρ(r)]表达式如下[24]:

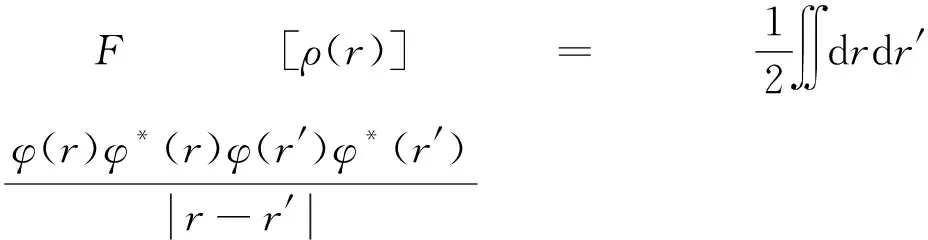
(3)

式中,T[ρ(r)]为动能泛函,φ(r)φ*(r)为电子密度泛函,Exc[ρ]为交换关联泛函。

1965年,Kohn和Sham给出可自洽求解体系基态密度的Kohn-Sham方程[26]。其表达式如下:

(4)

式中,V[ρ(r)]为电子势,εi为能量本征值,Ψi(r)为电子波函数,

1.3 交换关联泛函

目前广泛使用的交换关联泛函近似处理方式有局域密度近似(LDA)和广义梯度近似(GGA)两种方法[27]。

根据局域密度近似模型,交换关联泛函的表达式如下[26,28]:

(5)

fjg[ρ(r)]=fj[ρ(r)]+fg[ρ(r)],

(6)

式中,fjg[ρ(r)]是均匀电子气的交换关联能量密度,可以分成交换能密度fj[ρ(r)]与关联能密度fg[ρ(r)]两项。

GGA模型中交换关联泛函的表达式如下[29-30]:

(7)

实际上,两种近似模型需要根据实际情况进行选择。

1.4 电子结构计算

目前常选用的电子结构计算近似法有:赝势近似法、精确Muffin-Tin轨道法(EMTO)等[31-32]。

通过假想的赝势代表原子内的真实势能的方法叫做赝势近似法[33]。目前常用的赝势法是模守恒赝势(NCPP)[34]、投影缀加波赝势(PAW)[35]和超软赝势(USPP)[36]。

EMTO方法在球形范围内单电子势形式如下[37]:

V(ρ(r))≈V0+∑R[VR(rR)-V0],

(8)

式中,VR(rR)表示SR为半径的球形区域内势,V0是球形区域外常数势。

1.5 建模方法

目前常用的建模方法有3种[38]:虚拟晶体近似(VCA)[39,40]、特殊准随机近似(SQS)[41]和相干势近似(CPA)[42]等。

2 第一性原理计算应用

第一性原理计算在高熵合金的研究中可以预测相稳定性、硬度、弹性模量等参数来研究高熵合金性能及结构。

2.1 高熵合金强度研究中的应用

Chen等[43]利用第一性原理方法研究了Hf-Nb-Ta-Ti-Zr HEA的相分解对屈服强度的影响,证明可以通过将HEA视为伪二元系统来减小计算空间维数。同时合理地预测了等原子HfNbTaTiZr HEA会在临界温度1298K发生相分解,主要分解为具有BCC结构的富NbTa相和富HfZr相,且实验结果表明,随退火温度升高,析出相尺寸增大。如图1所示,随着退火温度的升高,析出强化效果降低,固溶强化效果增大,预测屈服强度与实验值基本一致。

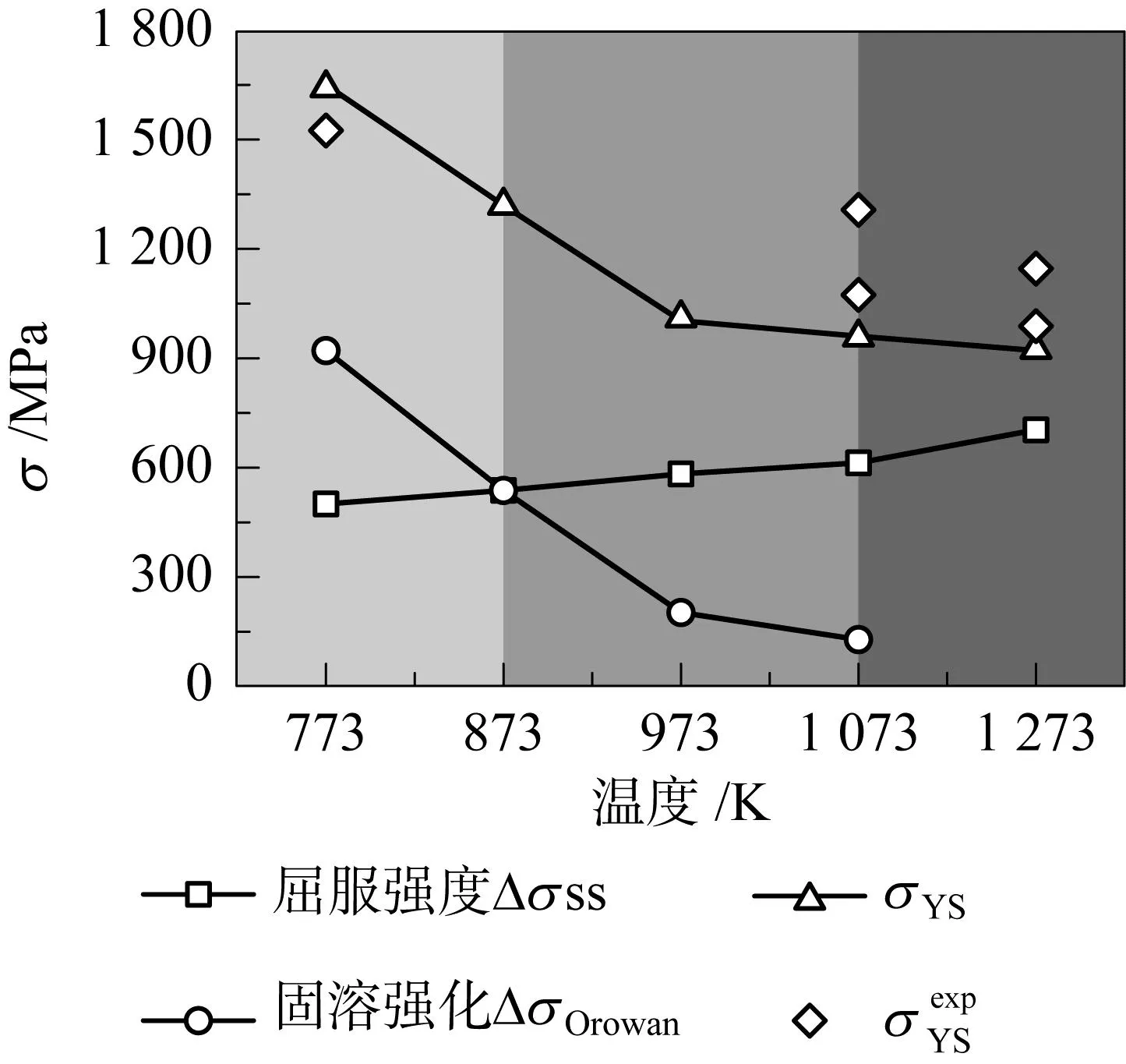
图1 不同退火温度下等原子HfNbTaTiZr的屈服强度及固溶强化和析出强化贡献[43]

丁欣恺等[44]通过第一性原理计算了NbMoTaWV高熵合金的力学性能,发现随着V含量增加,合金的强度会降低。Chang等[45]通过第一性原理计算研究了Mo添加对CoCrNiVMox合金晶格畸变和SFE的影响,如图2所示。通过使用均方原子位移(MSAD)估计局部晶格畸变效应,证实了Mo、 V元素的添加会产生严重的局部晶格畸变,这也是其屈服强度高的关键原因。同时,变形孪晶的比例会随着W的加入而降低[46]。此研究表明,可以通过确定适当的MSAD值来预测屈服强度和延展性的趋势,因为高熵合金的短程有序或纳米晶会影响位错运动、变形孪生等,通常有利于强度和延展性的提高[47-48]。

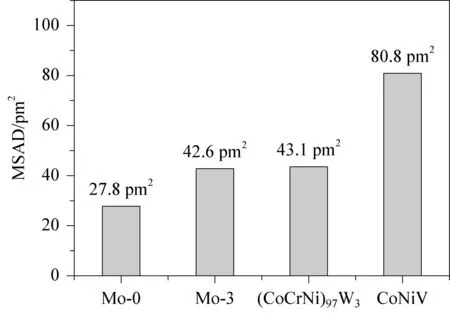
(a) 均方原子位移(MSAD)模拟晶格畸变

2.2 高熵合金相稳定性及弹性模量研究中的应用

Ma等[49]采用有限温度第一性原理方法研究了等原子高熵合金CoCrFeMnNi的热力学性质。通过计算T=0K和有限温度下各自晶体结构的自由能来研究HCP, FCC和BCC结构之间的相稳定性。图3为3种磁性状态:无磁性(NM)、铁磁性(FM)、无序局部矩(DLM)的HCP, FCC和BCC的自由能,对于DLM状态,预测在温度高于室温时最稳定的相为顺磁FCC相,与实验结果相符(即FCC DLM状态比HCP和BCC更稳定)[50]。研究表明,为可靠地预测HEA系统中的相稳定性,必须同时考虑振动、电子和磁熵贡献。

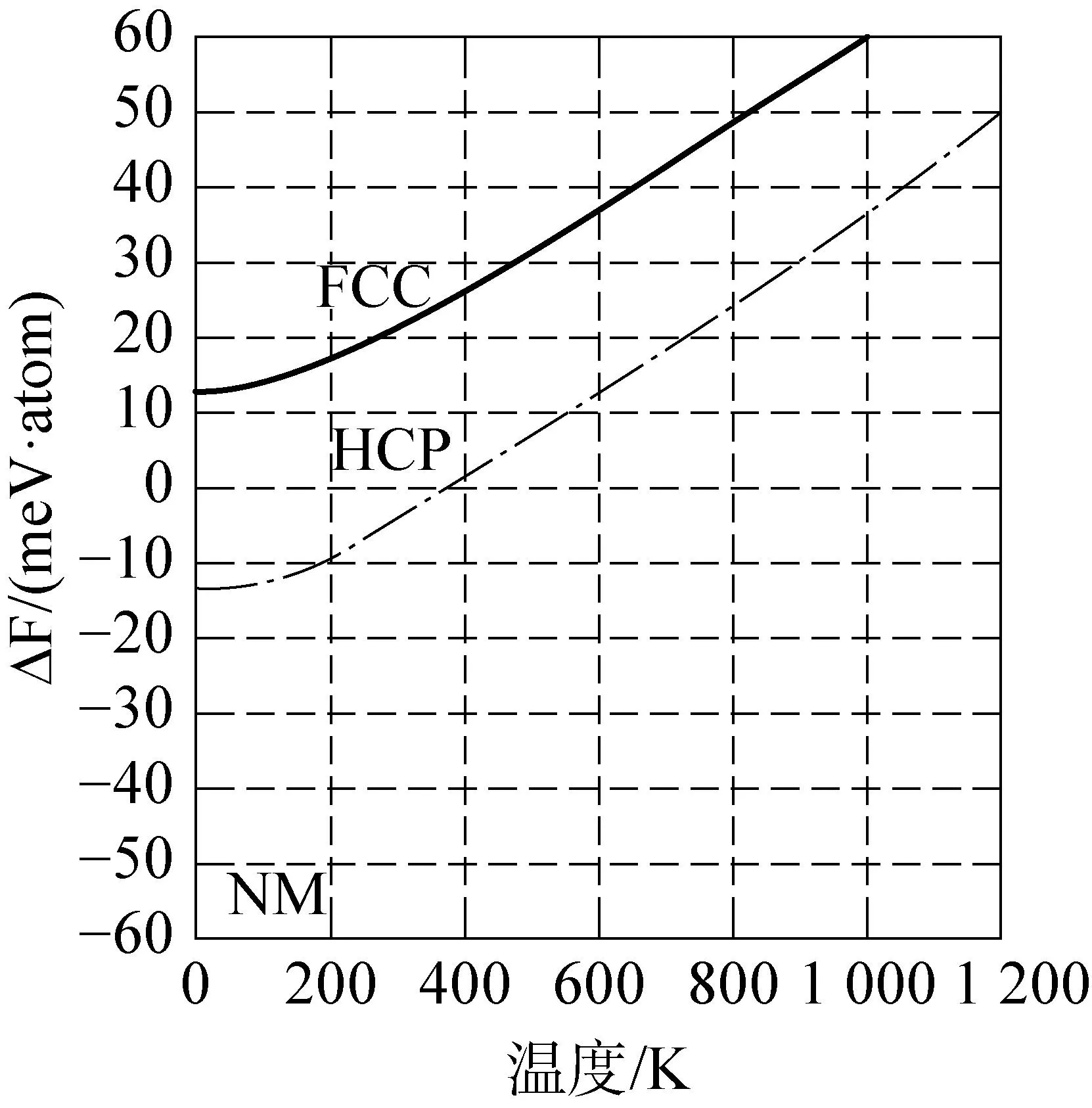
(a) NM态

熊青云等[51]通过第一性原理计算VTiTaNbAlx高熵合金的相稳定性发现,随着Al含量增加,平均价电子数减小,高熵合金BCC相结构的稳定性降低。Xia等[52]通过第一性原理计算模拟了900℃退火后Co1.5FeNi2V0.18Nb0.19Ta0.2(VNT)发生ε→δ相变,相关信息表明在900 ℃下δ结构比ε结构具有更低的形成能(较高的相稳定性)。

梁红玉等[53]通过第一性原理计算了Si/Ti掺杂对AICrCoFeNiMoTiySiy高熵合金弹性模量的影响规律,实验结果表明,当Ti质量分数为0, Si质量分数为100%时,高熵合金弹性模量最小。Wu等[54]通过第一性原理EMTO方法,结合CPA研究了等原子CoCrFeNi合金的有限温度弹性性质,EMTO-CPA方法在计算高熵合金弹性模量方面的可靠性已在高熵合金的应用中得到证实。除了原子振动和电子自由能外,该预测模型还包含了自旋波动(SFs)对CoCrFeNi弹性性质的贡献,既考虑了横向自旋波动(TSF)外,也考虑了纵向自旋波动(LSF),将3个子模型与作为温度函数的实验趋势进行比较。模拟结果如图4所示,因为SFs包含了弹性模量的温度导数,使得模拟和实验测量的趋势接近一致。

三个模型分别为振动贡献(Vib.)、振动和TSF贡献(Vib.+TSF)、所有因子贡献(Vib.+TSF+LSF)其中G和Y分别由阴影区域和无阴影区域标记图4 模拟和实验均质化多晶CoCrFeNi的剪切模量G和杨氏模量Y随温度的变化[54]

2.3 高熵合金耐腐蚀性研究中的应用

王勇等[55]通过第一性原理计算FeCr NiCoCu和FeCrNiCoMn高熵合金态密度与晶胞能量,得出FeCrNiCoMn高熵合金更加耐蚀的结论。这是由于FeCrNiCoMn高熵合金态密度达到最大值时对应的能量较低,结构更稳定,耐蚀更好。

Yen等[56]研究了退火态等原子AlCoCrFeNi三相合金在0.5 MHSO充气水溶液中的腐蚀机理。实验结果表明,B2相基体被优先腐蚀掉,而晶界FCC和迷宫状BCC依然存在,这与基于密度泛函理论的第一性原理计算的氢氧化物在(001)面上的形成能趋势一致。如表1所示,该研究用第一性原理计算的吸附在B2上的单层羟基离子的键能在每OH键或单位面积中都是最小的,这意味着B2相的稳定性是最差的,即B2相在充气水溶液中更容易受腐蚀,这与等原子AlCoCrFeNi三相HEA的SEM和EDS观察和分析一致。

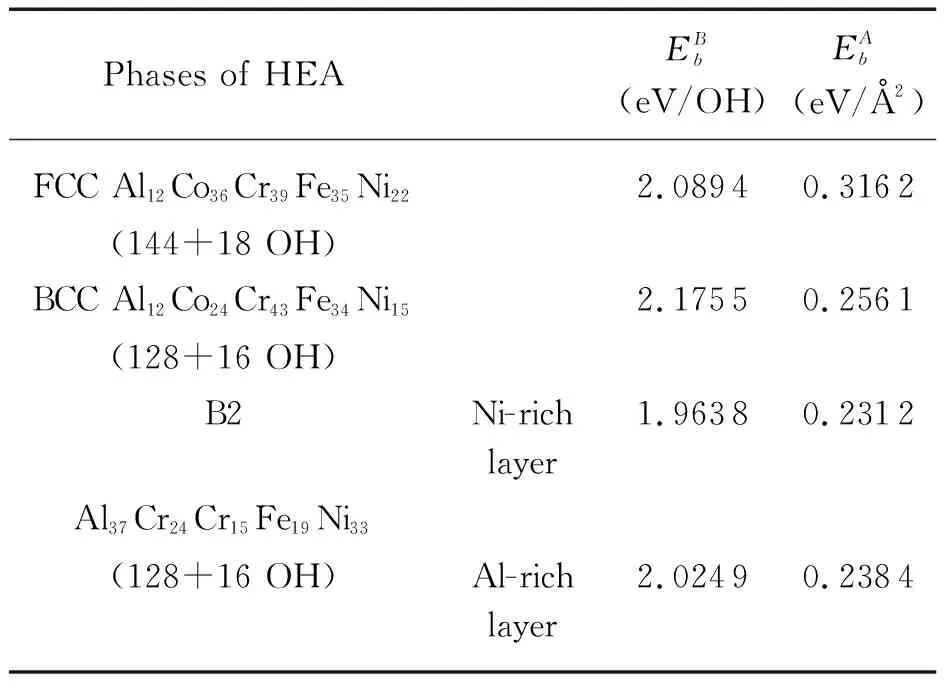
表1 AlCoCrFeNi中FCC、BCC和B2相(001)面上单层OH的平均键能和单位面积键能[56]

Wang等[57]通过第一性原理与热力学计算,研究了Cr-Fe-Co-Ni-Mo体系以设计和表征不同Cr和Mo含量的多组元单相FCC合金,不同成分合金体系的相计算结果如图5所示。证明了在保留FCC单相的同时添加高达15%摩尔分数的Mo是可能的,并且必须确保一定的Cr含量才能通过钝化确保耐腐蚀性能。由于铬合金化对腐蚀性能的促进作用是由于形成了保护性氧化层,Mo合金元素在不形成σ相时有利于耐腐蚀性,特别是在更具腐蚀性的含Cl环境中,因此设计出合适的Mo和Cr含量的合金对其耐腐蚀性至关重要。该研究通过第一性原理辅助热力学计算模拟,以及与实验相结合的方式,证明添加高达10%摩尔分数的Mo极大地增强了合金在含Cl的腐蚀环境中的耐腐蚀性。由此设计的五元合金Cr-25Fe25Co5Ni40Mo5和Cr15Fe10Co5Ni60Mo10(摩尔分数)表现出优异的耐腐蚀性。

图5 计算1273K下五元Cr-Fe-Co-Ni-Mo相组成[57]注: 右边为准三元FeCoNi相组成图

Qiu等[58]基于密度泛函理论(DFT)的第一性原理计算AlTiVCr合金的热力学和结构性质,采用原子探针层析成像和X射线衍射表征,揭示B2相具有较低的形成焓(-9.30kJ/mol, atom),在低温下比无序的BCC相(-1.25kJ/mol, atom)更稳定,同时形成吉布斯自由能更低,模拟结果如图6所示。此外,APT和DFT分析的耦合能够帮助识别晶格占位,从而提供了合金结构及力学、腐蚀性能相关信息,是适用于高熵合金研究的重要方法。

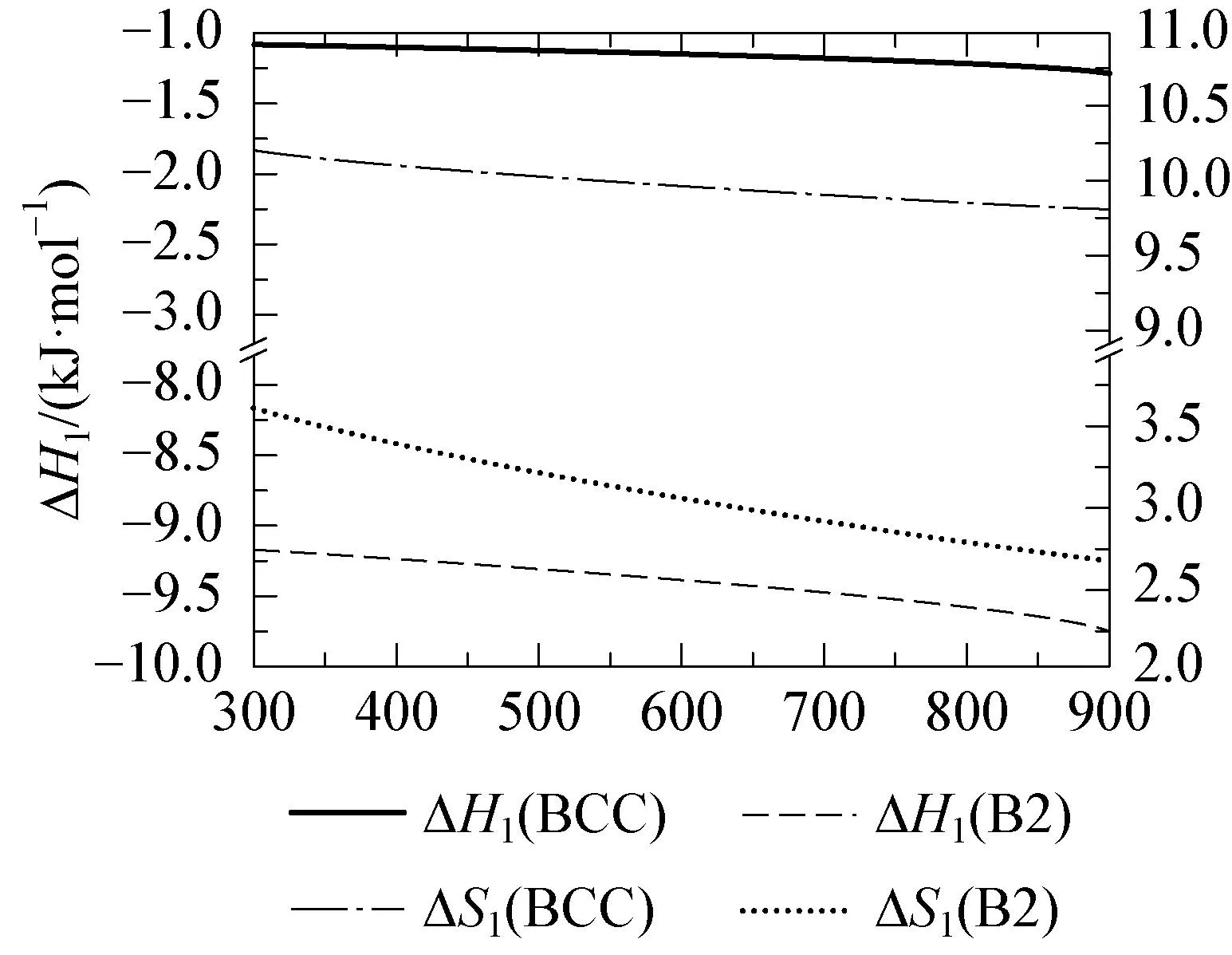
(a) BCC和B2相AlTiVCr的形成熵ΔSf和形成焓ΔHf随温度的变化

2.4 高熵合金硬度研究中的应用

贺战文等[59]通过第一性原理软件Materials Studio计算了FeNiMnCu0.2Alx高熵合金的能带在-15～15eV间更密集,表明此时合金原子间相互作用更强,因而预测在该能量范围内形成的高熵合金硬度更高。Furuhara等[60]利用第一性原理计算了N原子团簇的总能量和相应的相互作用能,如图7所示。当在位于(001)α面的M原子的次近邻位置添加N原子时,团簇能量增加。然而,团簇能量随着N原子数的增加而单调递减,相应的相互作用能在更高的N含量下更强,从而获得更高的硬度。这些趋势与图7中Fe—V—N和Fe—Ti—N体系中单层N—S团簇的观察和蒙特卡罗模拟结果很好地对应。在Fe—Al合金中添加Ti或V,即使添加低浓度(例如0.1%,摩尔分数)时,也会加速纳米氮化物的析出,复杂合金氮化物细小弥散分布是获得良好表面硬化的主要原因。

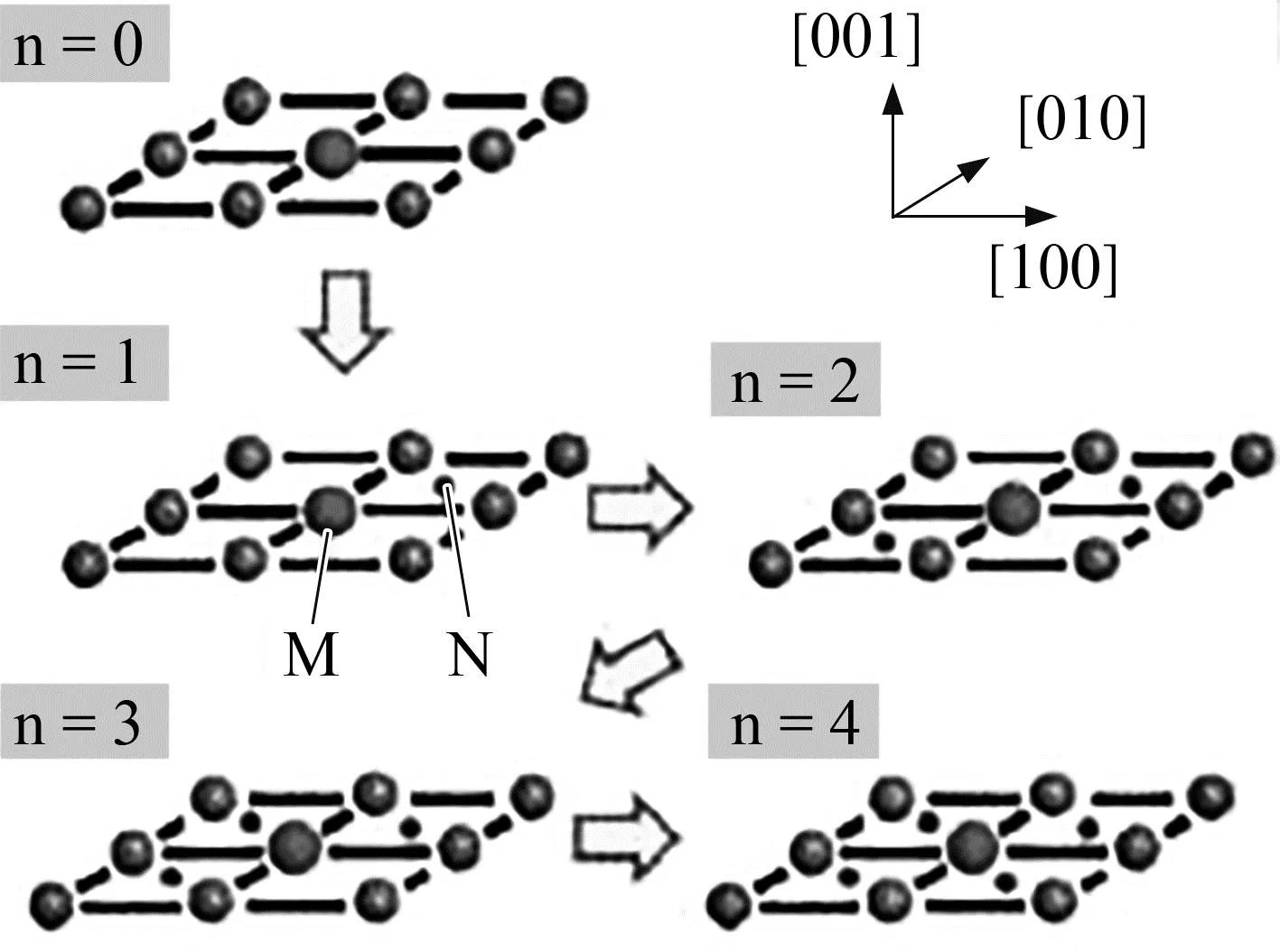
(a) 计算氮(N)和置换型合金元素(M)的原子排布

Ye等[61]研究了间质氧或氮添加对NbTiZrHf高熵合金在塑性起始过程中的硬化作用,通过定量统计分析和DFT计算,分析了间隙氧/氮的硬化机制。并且该研究还采用同步辐射X射线衍射[图8(g)和(h)]和透射电子显微镜证实了氧/氮原子确实作为间隙溶质存在。在理想剪切强度的DFT计算中,考虑了两种类型的滑移系统,即{110}<111>和{112}<111>剪切变形,如图8所示,这些间隙溶质可以提高启动塑性所需的临界剪切应力,并且间质氮比间质氧产生更大的硬化效应。DFT计算清楚地揭示了间隙氧/氮可以同时提高NbTiZrHf高熵合金的能量和理想剪切强度,且氮的影响略大于氧,这与纳米压痕结果一致。并且DFT计算还表明氧/氮间隙原子诱导了局域电荷转移,提高了晶格内聚力,这可能是当前间隙合金化高熵合金中强度和硬度提高的原因。

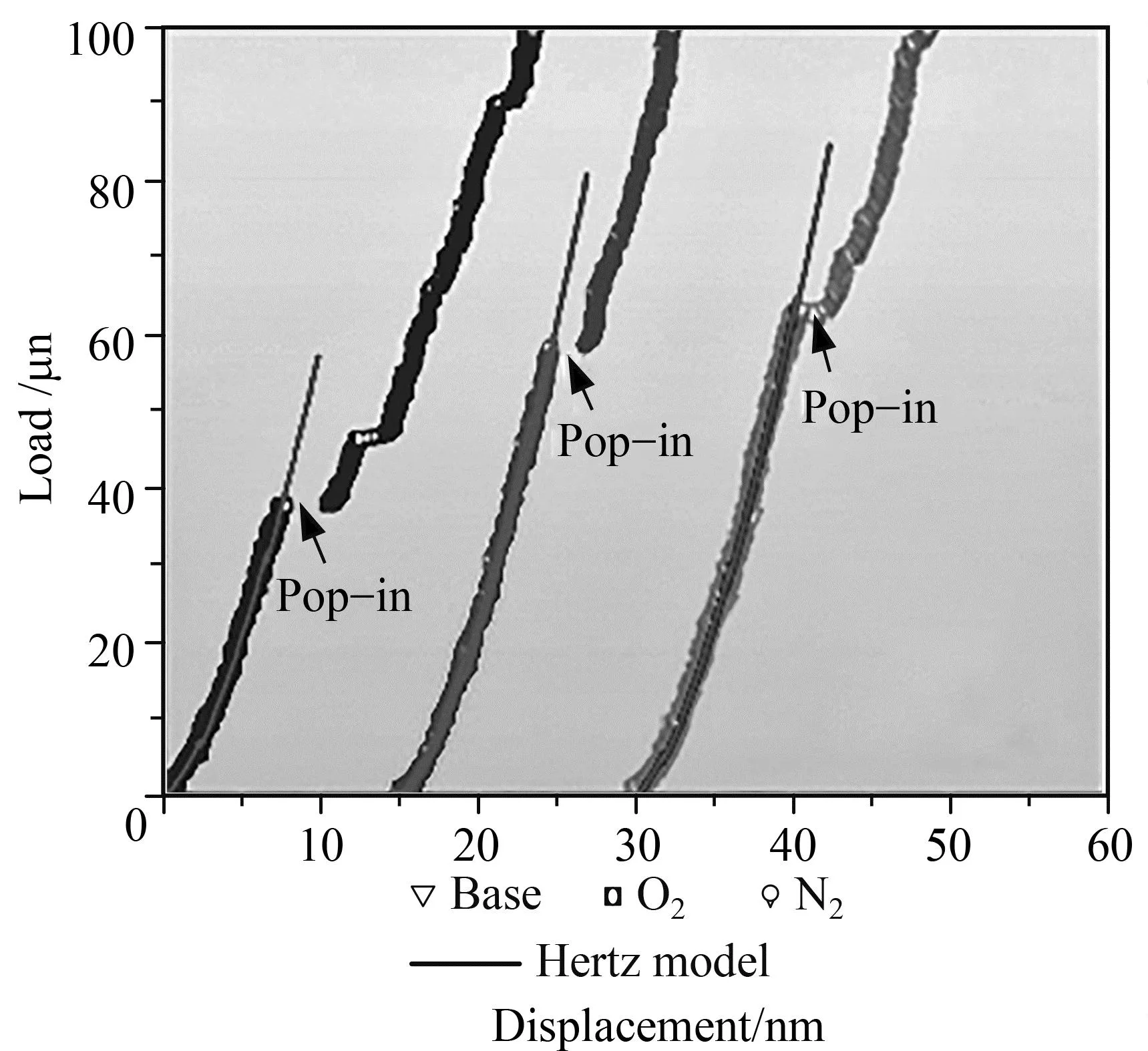
(a) NbTiZrHf高熵合金和间隙合金化后压痕载荷—位移曲线及弹出标记

3 总 结

高熵合金具有比传统合金更突出的优异性能,但因为高熵合金有多种合金组分和微观结构,第一性原理计算在高熵合金设计中存在诸多困难,所需要的计算能力随着组元增加而大幅增加,目前,对高熵合金设计理论与方法的研究还处于初级阶段。尽管有些实验已经证明可以预测高熵合金物理性质,但由于精度和计算力问题,第一性原理计算需要通过实验验证其有效性,对非等原子比合金的探索工作应用较少。因此,未来研究应针对这些问题进行改善第一性原理计算模拟,从而拓宽其在高熵合金设计以及性能研究中的应用。