虚拟元方法求解混合边界条件下的线弹性问题

马俊驰, 程新博, 梁晓坤

(辽宁师范大学 数学学院,辽宁 大连 116081)

线弹性问题在材料科学、桥梁结构、土木工程和航空航天[1-3]等领域具有广泛的应用.目前线弹性问题已有多种数值求解方法,如有限元方法[4]、有限差分法[5]、有限体积法[6]、弱有限元方法[7]、虚拟元方法[8]等.有限元方法在我国最早是由冯康先生[9]提出的,并形成一套系统的数值计算方法.有限元方法概念清晰、描述简单、应用广泛,但在剖分单元的选择上具有一定的局限性,比如多边形(多面体)网格,而虚拟元方法[10]在网格处理上具有较好的灵活性,其作为有限元方法的推广受到广泛关注.本文主要研究应用虚拟元方法求解二维混合形式线弹性问题,对于该问题可以加强应力张量的对称性,这种方法的挑战在于混合形式线弹性问题的离散化.文献[11]中对应力张量的对称性进行了弱化,引入旋转张量作为另一个未知数,主要讨论具有齐次Dirichlet边界条件的二维线弹性问题.而本文将边界条件推广到Dirichlet和Neumann的混合边界条件.文献[12]研究具有混合边界条件的二维线弹性问题的三种弱形式,给出虚拟元离散化的一般过程,并没有给出详细的虚拟元空间构造、误差估计等,本文将研究具有混合边界条件的弱对称形式的线弹性问题.

1 连续性问题

定义Ω⊂2为具有Lipschitz连续边界的有界区域,边界为Γ=∂Ω,且Γ的两个子集ΓD,ΓN满足Γ=ΓD∪ΓN,ΓD∩ΓN=∅.记弹性体所受外力的单位体密度为f∈[L2(Ω)]2.线弹性问题可表述为,求σ,u满足

(1)

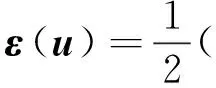
2 虚拟元方法

2.1 变分形式

定义空间Σ:=H(div;Ω),U:=[L2(Ω)]2,X:={Υ:Υ∈[L2(Ω)]2×2,Υ反对称}.

通过分部积分法,得到问题(1)的变分形式:找到(σ,u,ω)∈Σ×U×X,使得

(2)

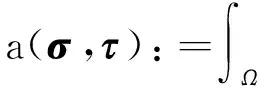
据文献[13]得双线性形式a(·,·)满足连续性和强制性,b(·,·),c(·,·)满足inf-sup条件,则问题(2)的解存在且唯一.

2.2 构造虚拟元空间

首先对区域Ω进行剖分,设{Th}h是将Ω分解为元素E的序列,h表示{Th}h中元素的最大直径.假设存在整数N和正实数β,使得对于每个h和每个E∈{Th}h,满足:①E的边数小于等于N;②E的最短边与E的直径hE之比大于β;③E相对于半径为βhE的球上的每个点呈星形.

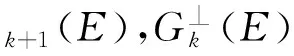
对于整数k≥1,定义局部应力空间为

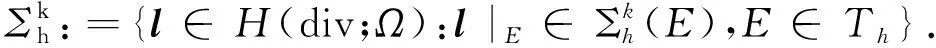
为了对误差进行估计,引入下列投影算子与插值算子.

(3)

(4)

对于足够光滑的函数q和l,以下估计成立

(5)

在每个单元E上,

(6)

2.3 虚拟元离散

基于上述剖分以及空间的定义,首先将双线性形式进行离散,

由于双线性形式b(·,·),c(·,·)可以通过选择适当的空间Σh,Uh,Xh来计算,所以不需要引入全局项b(·,·),c(·,·)的任何近似值,即bh(·,·)=b(·,·),ch(·,·)=c(·,·).

变分形式(2)的离散格式为:找到(σh,uh,ωh)∈Σh×Uh×Xh,使得

(7)

其中,div Σh⊆Uh.

上述的局部离散双线性形式具有以下的3种性质.

引理1[16]存在整数k≥1,对于所有的E∈Th,都有[Pk(E)]2×2⊂Σh|E,

(2) 稳定性:存在两个不依赖于h和E的正常数α*和α*,使得

根据引理可知离散双线性形式ah(·,·)具有连续性、强制性,b(·,·),c(·,·)满足离散inf-sup条件,则离散形式(7)的解存在且唯一.

2.4 误差分析

根据文献[11]可得离散问题的收敛性,下面对离散问题的误差进行分析.

引理2[13]存在一个常数C>0,使得

对于误差分析,给出如下定理并证明.

定理1问题(7)有唯一解(σh,uh,ωh)∈Σh×Uh×Xh,L2误差估计为

‖σ-σh‖0+‖u-uh‖0+‖ω-ωh‖0≤C(μ)(hk+1‖σ‖k+1+hk+1‖u‖k+1+hk+1‖ω‖k+1),

其中,C(μ)是一个与λ无关,但依赖于μ的正常数.

根据问题(2)和问题(7),为了方便起见,这里取gD=0,有

ah(eσ,τh)+b(τh,eu)+c(τh,eω)=

(8)

(9)

(10)

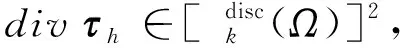
(11)

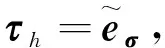
再根据式(11)有

(12)

令引理2中vh=0,θh=eω得到τh∈Σh满足c(τh,eω)≥C‖τh‖0‖eω‖0,由式(8)有

(13)

根据式(12),式(13)得到估计

接下来,根据三角不等式和式(5),式(6)可以推得

‖σ-σh‖0+‖ω-ωh‖0≤C(μ)(hk+1‖σ‖k+1+hk+1‖ω‖k+1).

(14)

(15)

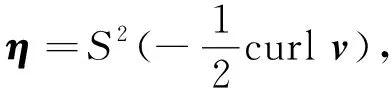
根据问题(15)以及式(4),式(8)和τ的对称性有

其中,

接下来由一致性、连续性和式(14)可得

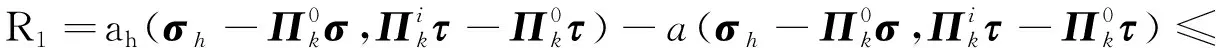
同理可得

R2≤C(μ)(hk+2‖σ‖k+1+hk+2‖ω‖k+1)‖eu‖0,

R3≤C(μ)(hk+2‖σ‖k+1+hk+2‖ω‖k+1)‖eu‖0,

将R1,R2,R3,R4代回原式,两边同时除以‖eu‖0就可以得到

(16)

由三角不等式和式(16)可得

‖u-uh‖0≤C(μ)(hk+1‖σ‖k+1+hk+1‖u‖k+1+hk+1‖ω‖k+1).

结论得证.

3 数值实验

本文考虑带孔的板模型,其中,孔的半径为a=0.4.考虑混合弱形式线弹性问题(1),其中,弹性模量为E=103,泊松比为υ=0.3.弱对称形式经过刚度矩阵的变换可化为强对称形式,即以位移和应力作为问题的解,因此数值实验中只考虑位移与应力.根据文献[17]可得,位移的精确解为

应力的精确解为

其中,(r,θ)为极坐标,θ是从x轴的正半轴开始沿逆时针方向的夹角.对于平面应变状态,κ=3-4υ.μ为Lamé常数.

首先对区域进行剖分,剖分区域为Ω=Ω1/Ω2,其中,

图1给出剖分区域Ω的多边形网格剖分,其中,网格剖分数n分别为46、539、3592和21916.

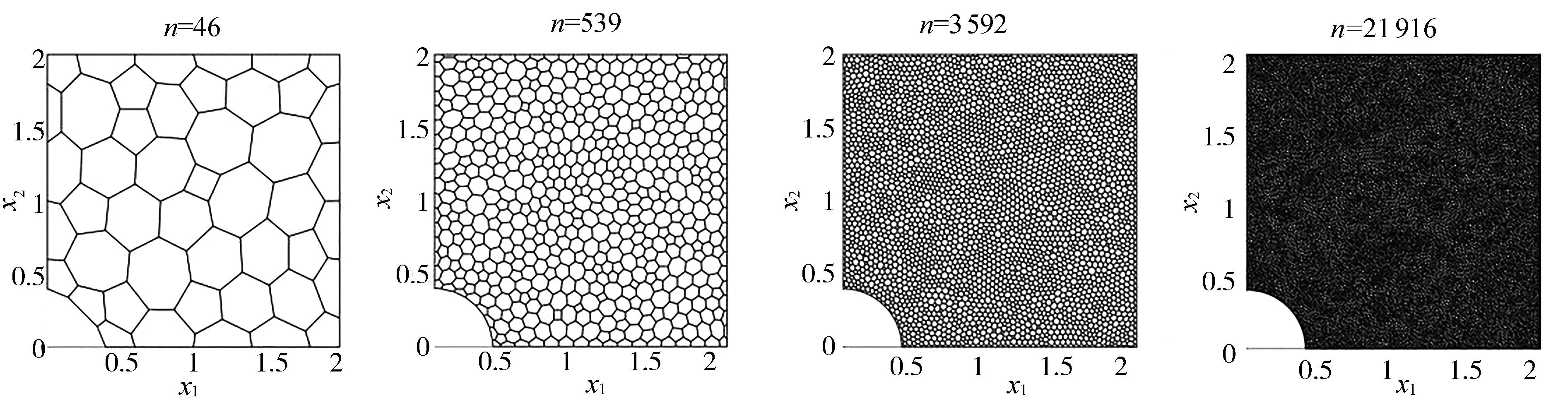
图1 不同网格数对应的剖分图Fig.1 The division diagram corresponding to different mesh numbers

图2给出网格剖分数n为46、539、3592和21916的位移与应力的数值解,其中,u1,h,u2,h为位移的数值解,σ11,h为应力的数值解.

图2 不同网格数对应的位移与应力的数值解Fig.2 Numerical solution of displacement and stress corresponding to different mesh numbers

其次应用虚拟元方法求解上述线弹性问题,得到数值解uh和σh与精确解u和σ之间的L2范数下的相对误差,讨论不同网格剖分数下位移与应力的相对误差.

表1给出了不同网格剖分数对应的位移与应力的相对误差,其中,uerr(L2)表示L2范数下位移的相对误差,σerr(L2)表示L2范数下应力的相对误差,其中,uerr(L2)=‖u-uh‖0,σerr(L2)=‖σ-σh‖0.

表1 不同网格数对应的位移与应力的相对误差Table 1 Relative error of displacement and stress corresponding to different mesh number

从表1可以看出,随着网格剖分数的增加,位移与应力的相对误差都呈明显减小的趋势,这与第三节的理论分析相一致,验证了误差估计的有效性.

4 总 结

本文主要讨论带Dirichlet和Neumann混合边界条件的二维线弹性问题的虚拟元方法.线弹性问题研究的是在一定假设条件下,弹性体受到外力或者其他外界作用时,弹性体内的应力、应变和位移之间的关系.本文研究混合弱形式的线弹性问题,以位移、应力和旋转张量作为研究问题的解,在混合边界条件约束下,通过变分原理得到弱形式线弹性问题的变分格式,然后通过构造虚拟元空间和自由度对变分形式进行离散.进一步通过定义投影算子与插值算子处理误差估计,最后通过实际问题带孔的板,验证了理论分析的有效性.