自升式平台可靠性分析法及海上模态测试验证

冯 勤，刘 续，陈 达

（中国石油化工股份有限公司上海海洋油气分公司，上海 200120）

目前，随着对能源需求的加剧，海洋油气资源的勘探开发力度越来越大。自升式钻井平台移动性良好，作业水深范围较大，在中深水海洋油气资源勘探开发中发挥着主导作用。但是，在实际作业过程中，由于环境载荷、操作载荷和海床地质条件等因素，自升式平台结构有可能发生局部损坏失效。因此，亟需对自升式钻井平台的结构安全性的判断标准进行研究。

由于自升式平台结构刚度相对较弱，结构分析需要充分考虑结构动力响应特征。平台动力振动特性的研究主要有两种方法，一是利用计算机仿真模型进行研究，二是通过实验进行研究[1]。但由于自升式钻井平台结构复杂，尺寸较大，给自升式钻井平台的计算机仿真研究和实验研究带来了较大的困难。一方面体现在自升式钻井平台计算机仿真不够精确，常常无法真实地反应其结构动力特性[2]；另一方面海上实验条件恶劣，无法准确地掌握自升式钻井平台海上真实振动信号[3]。目前，自升式钻井平台的实验研究主要以缩放模型为主，通过振动台和激振器提供外界激励的方法对自升式钻井平台缩放模型进行实验研究，而较少进行海上现场实验研究[4]。

本文以“勘探二号”自升式平台为研究对象，建立了平台USFOS 仿真有限元模型，首次提出了建立在失效概率分析基础上，采用有限元仿真模型判断自升式平台的可靠性的计算法；同时，利用有限元模型计算得到平台的固有周期与振型，并提出了以加速度传感器来测试平台结构振动特征及验证数字仿真模型的思路，验证了有限元仿真模型的准确性。

1 可靠性评估理论

可靠性评估基于海洋结构设计规范中的极限状态中的破坏准则，自升式平台结构的失效概率Pf为载荷水平超过结构抗力的概率，其失效概率Pf表达式为：

式中：n为环境载荷方向数目，个；PE为环境载荷的年超越概率。

根据Shell 石油公司的结构可靠性计算模型可知[5]，年超越概率PE为超过载荷水平E 的长期载荷指数分布函数，表达式为：

式中： A和E0为环境载荷分布的特征因子，推荐A=180，E0=0.102。E 为超过载荷参数，该参数是判断自升式平台结构失效概率计算的关键基础参数。选取怎样的基础参数进行PE计算显得尤为重要。因此，根据相关研究，参考平台的结构失效概率计算中采用的结构储备强度因子RSR（Reserved Strength Ratio）作为基础参数，其表达式为：

式中：Fult为结构倒塌时极限载荷，N；F100为100 年重现期环境载荷，N。

自升式平台与导管架平台在结构强度和刚度分析方面具有很多相似之处，结构在海上环境荷载下的结构失效特征和规范监测标准类似。因此，自升式平台结构的可靠性分析参考Shell 石油公司对导管架平台研究的可靠性指标，结构失效概率阈值定为3.0×10−5。采用此可靠性评估理论计算得到自升式平台结构失效概率，若计算值低于3.0×10−5，则认为自升式平台是可靠安全的，否则被认为是不可靠不安全的。

可靠性评估的流程主要分为如下四步骤：

（1）根据自升式平台结构特征建立USFOS 结构力学模型；

（2）选取百年一遇8 个方向的环境荷载（波、流、风）作用于平台结构，利用海洋工程结构分析计算软件USFOS 进行垮塌分析，计算得到平台在不同环境方向环境荷载作用下的结构储备强度因子RSR值；

（3）根据Shell 标准计算平台的年超越概率PE和失效概率Pf；

（4）基于Shell 海洋结构物失效概率指标与平台失效概率Pf进行对比，评估自升式平台结构的安全可靠性。

2 有限元仿真模型

“勘探二号”平台桩腿为桁架式桩腿，艏一艉二，分别编号为船艏1#、左舷3#、右舷2#桩腿。每个桩腿的横截面形式是三角形，每个桩腿下部均设有多边形的桩靴结构。平台围阱区为方形，在艏部#2～#7 肋位设置一个围阱区，在艉部#19～#25 肋位设置二个围阱区。围阱区上端设有升降室，升降装置位于升降室内，用以升降及约束桩腿垂直位移。升降室的顶部及围阱区底部设有上、下导向，用以约束桩腿与船体之间水平相对运动。

结合“勘探二号”平台的结构特点，本文采用海洋工程非线性结构分析软件USFOS 进行建模[6]。

（1）根据“勘探二号”平台的结构特点，使用壳单元和梁单元来模拟自升式平台的结构，通过合理的简化，将平台结构离散为空间的梁-壳组合模型。平台船体的主甲板、底板、横舱壁以及纵舱壁等主要结构采用壳单元进行相应的模拟，主要采用四节点壳单元，少量使用3节点壳单元；船体纵桁、强横梁等构件采用梁单元进行模拟，骨材、扶强材以及加强筋等结构未考虑。

（2）桩腿主要由弦杆、水平撑杆及斜撑杆等组成，采用梁单元进行模拟。

（3）桩腿和船体采用具有适当刚度的梁单元进行特殊的结构布置模拟齿轮齿条连接装置，以反映连接区域的相对柔性。

（4）桩靴结构采用等效刚度的梁单元空间结构模拟，桩靴底部设置为铰支约束。

（5）结构垮塌分析采用结构材料非线性分析方法，充分考虑了材料屈服后的结构表现状况。

根据以上模拟处理方法建立“勘探二号”平台USFOS 有限元模型（图1）。

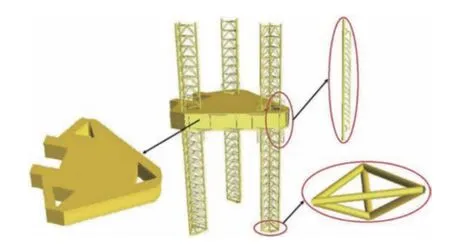
图1 “勘探二号”平台有限元模型Fig.1 The finite element model of “Kantan 2”

3 可靠性分析

基于自升式平台在位作业的特点，以及遭受意外突发情况的可能性，着重考虑桩腿水线处和桩靴入泥处的弦杆、水平撑杆和斜撑杆遭遇意外情况后杆件受损失效后的情况；考虑到平台具有一定的对称性及意外情况的复杂性，重点考虑1#和3#桩腿的杆件受损失效，杆件编号示意图见图2～图3。根据平台遭受意外突发情况的可能性及最恶劣工况的组合，着重考虑了12 种工况，工况计算见表1。平台载荷参考“勘探二号”平台操船手册，平台及固定载荷、可变荷载以及大钩活荷载以平台等效密度的方式施加在全船上，通过调整重心使三个桩腿的反力大致相同。井架及底座荷载按照下底座在风暴工况下和船体的滑道梁接触位置，施加在实际接触点上。由于环境载荷作用平台的方向不同，对每种工况考虑0°、45°、90°、135°、180°、225°、270°和315°八个不同方向环境载荷作用进行垮塌分析，计算得到不同工况下不同方向的RSR 值，从而计算自升式平台的结构可靠性的年度失效概率，其结果见表2。

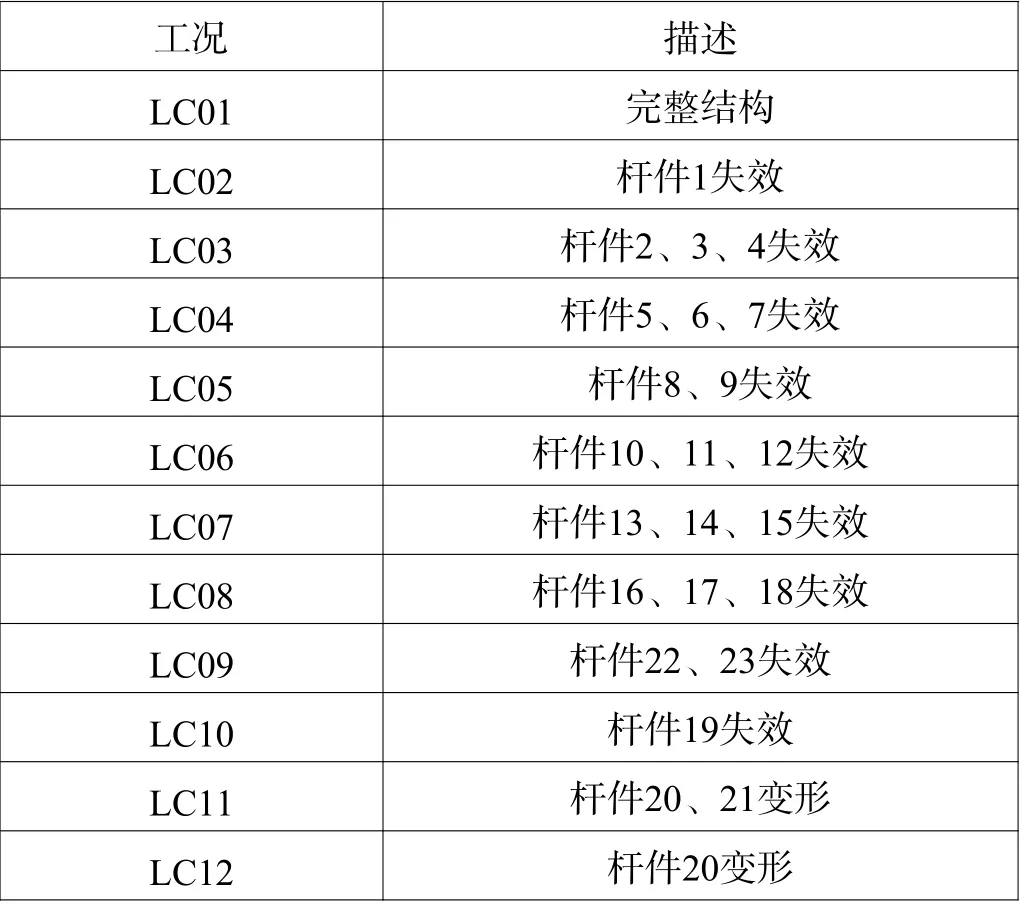
表1 工况计算表Table 1 Load cases

表2 平台结构可靠性概率值Table 2 Reliability probability of platform structure

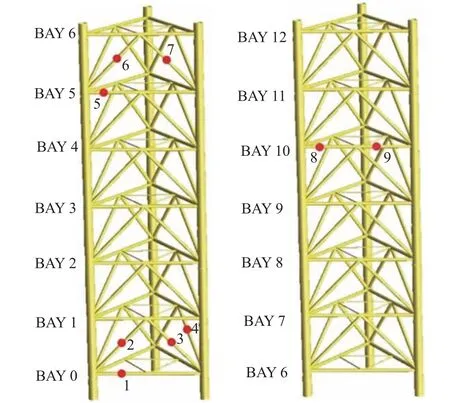
图2 1#桩腿杆件编号图Fig.2 Elements ID of 1# leg

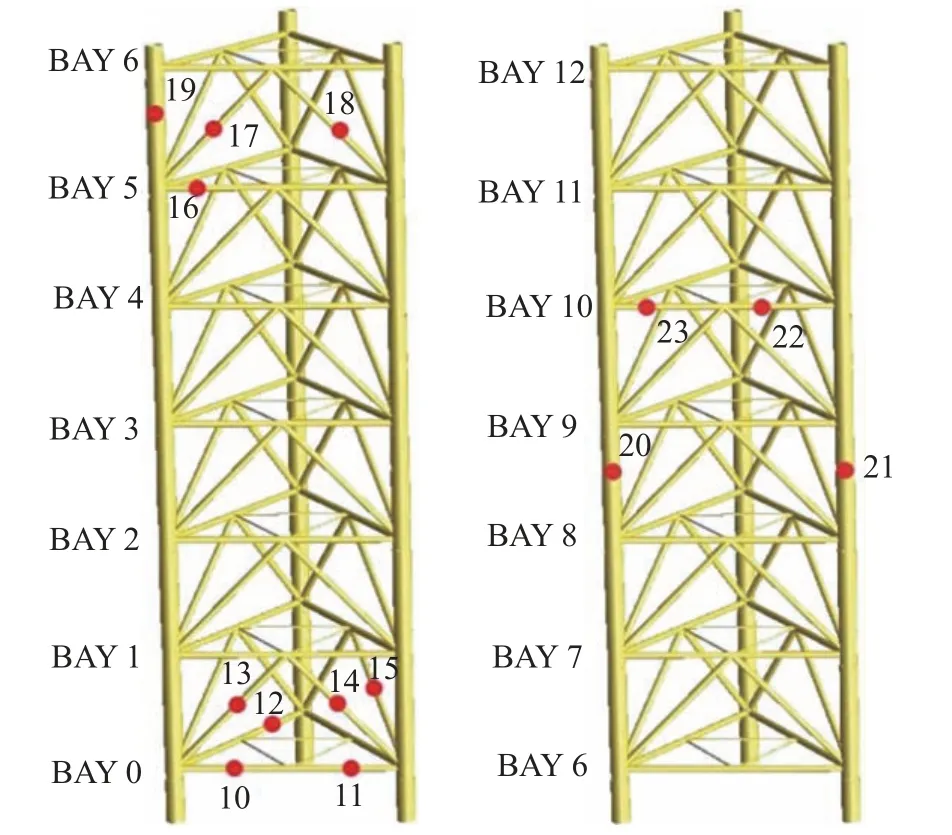
图3 3#桩腿杆件编号图Fig.3 Elements ID of 3# leg

从表2 可知，工况LC10、LC11 和LC12 年失效概率都大于3.50×10−5，超过可靠性判断指标，平台结构不能继续作业。

4 模态测试方案

4.1 测试模型

为真实有效地获得试验数据，选取“勘探二号”自升式平台作为结构模型，采用海上试验方法进行测试试验。“勘探二号”平台为自升式桁架结构，由平台船体、桁架式桩腿、升降系统和桩靴四部分结构组成。平台船体为多边形箱体结构，由5 道纵舱壁和5道横舱壁将箱形平台主体划分成若干舱室，平台有内外两层底板。“勘探二号”平台尺寸为长71.9 m、宽64.6 m、高125.9 m。

4.2 测试系统

由于压电式加速度传感器具有响应频带宽、灵敏度高、信噪比大、结构简单、工作可靠、重量轻、体积小、对被测件的影响小以及安装使用方便等优点[6-9]，同时考虑到自升式平台结构响应的频率范围，自升式平台振动测试系统选取压电式加速度传感器。

结合试验研究数据的需求，考虑到自升式钻井平台结构响应的频率特征，确定结构测试系统主要由传感器、数据采集系统和实时显示软件三部分组成。加速度传感器通过传输线缆连接到数据采集系统，数据采集系统经USB 连接线将自升式平台时域振动信号数据和经傅里叶变换（FFT）频域数据实时呈现在软件显示界面上。

平台桩腿位置选择1A202E 低频压电式加速度传感器，平台甲板位置选择2D001 速度传感器，甲板上放置一台32 通道的DH5983 便携式动态信号测试分析系统，利用USB3.0 与计算机终端通讯。表3 和表4为1A202E 低频加速度传感器和2D001 磁电式低频速度传感器的主要技术指标。数据采集系统选用DH5983便携式动态信号测试分析系统，DH5983 通过USB3.0与计算机终端连接。

表3 1A202E 低频加速度传感器Table 3 The 1A202E low frequency acceleration sensor

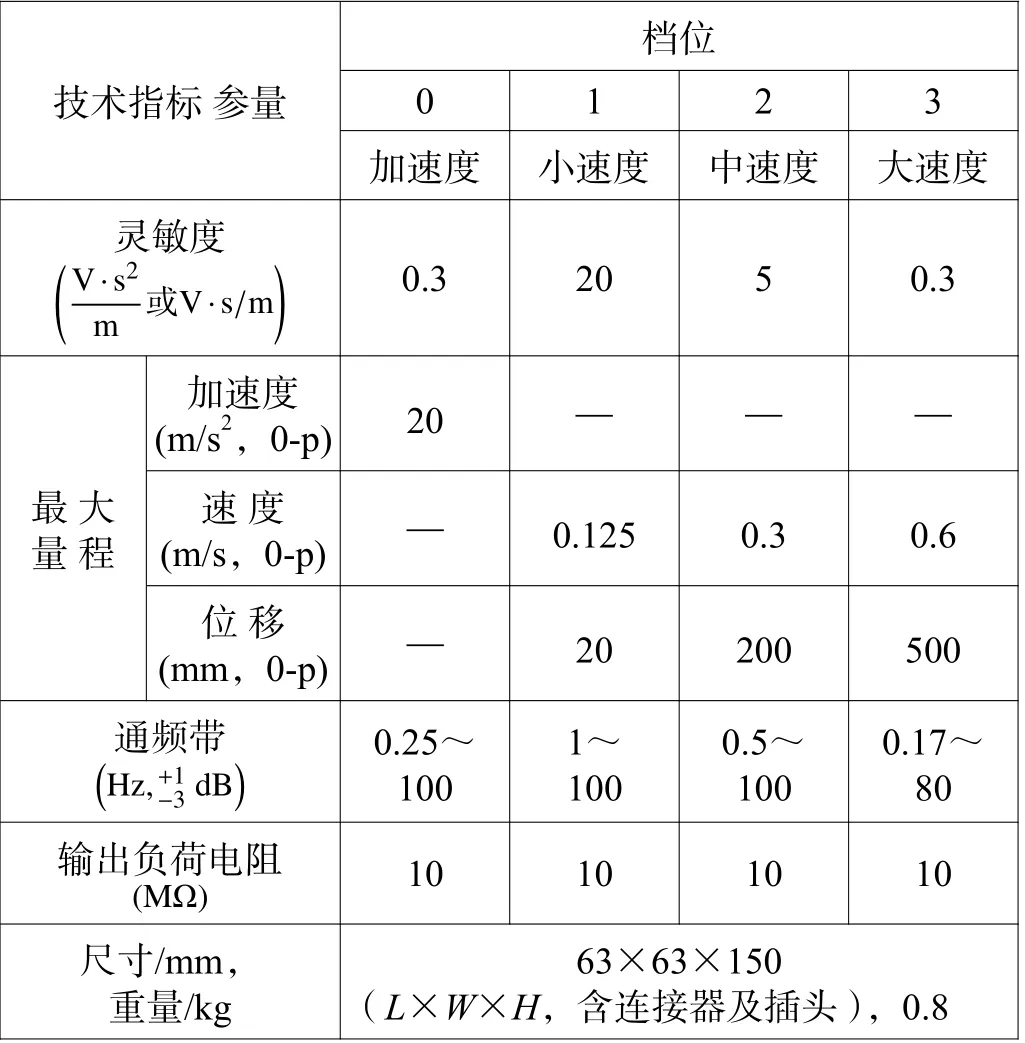
表4 2D001 磁电式低频速度传感器Table 4 The 2D001 magnetoelectric low frequency speed sensor

4.3 测试设计方案

试验测点布置应遵循以下原则：（1）安放在平台及船体连接处；（2）安放在刚度变化较明显的位置处；（3）尽可安放在平台受力均匀处；（4）左右应对称配置。

根据测点布置原则，以及自升式钻井平台的结构特点，同时考虑到试验数据的精确性，优化设计了“勘探二号”平台测试试验测点。平台每个桩腿各布置1 个测点，平台甲板上布置1 个测点，围阱区布置1 个测点，共计5 个测点，每个测点测量X、Y、Z三个方向的时间信号。

5 现场测试及分析

5.1 现场实施

根据结构测试试验方案，采用海上现场安装实施方式进行试验测试，1A202E 压电式加速度传感器采用磁力座安装方式固定在桩腿上，2D001 速度传感器采用橡皮泥固定在平台甲板上，现场数据采集系统见图4。

图4 现场数据采集系统Fig.4 The site data acquisition system

5.2 试验数据分析

结构测试系统现场安装调试结束后即开始数据采集，采集频率为10 Hz，现场每个测点的部分测试原始信号见图5(a)～图5(e)。

图5 测点1～5 现场测试原始信号Fig.5 Monitoring date of point 1～5 on site

采用傅里叶变换[10]对现场测试数据进行处理，处理后得到各个测点的相应的频谱数据试原始信号（图6(a)～图6(e)）。

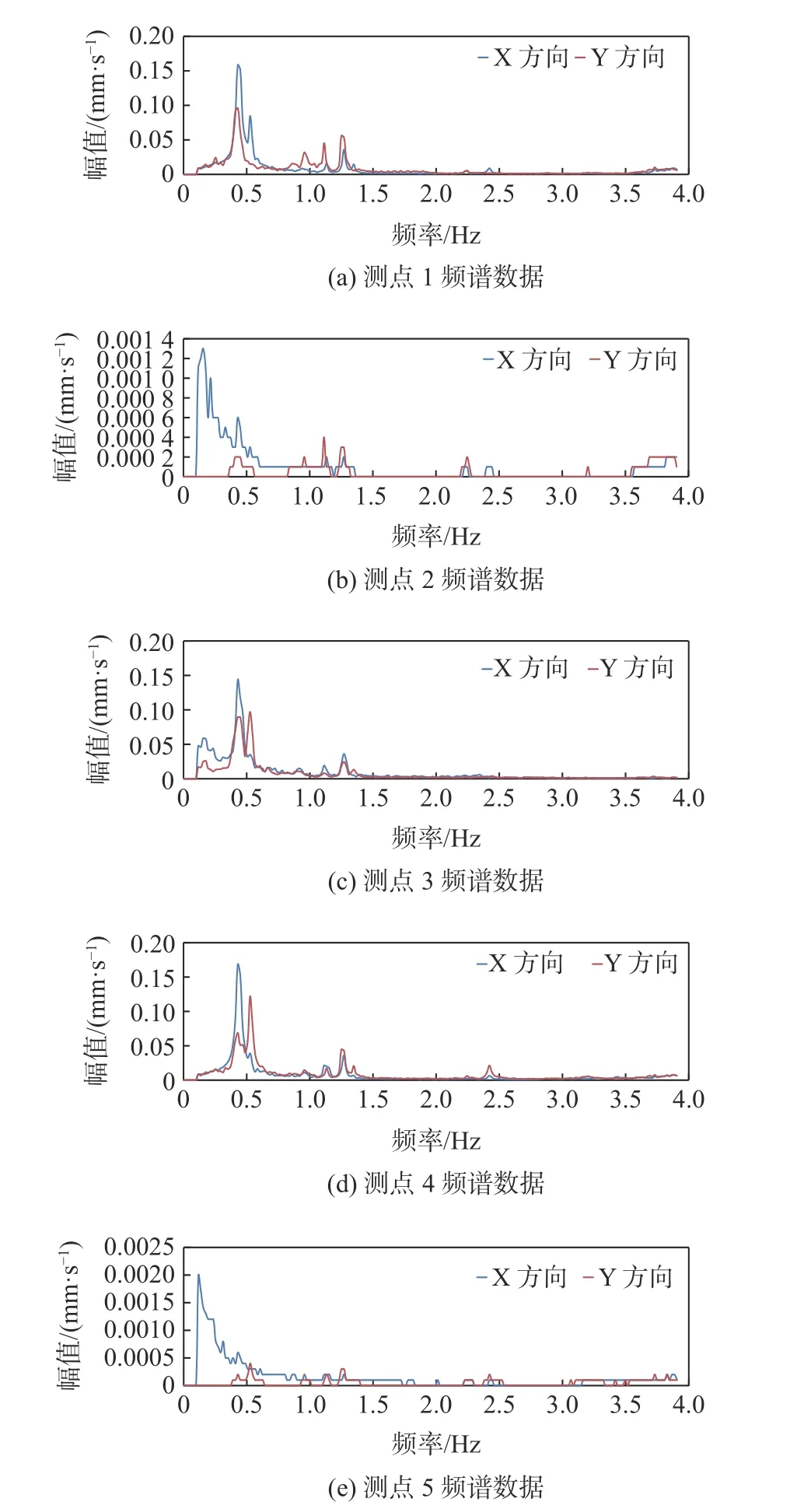
图6 测点1～5 频谱数据Fig.6 The spectrum data of point 1～5

5.3 测试结果与仿真分析对比

提取各个测点X、Y 两个方向的频谱数据，然后进行加权平均，计算得到各个测点的自振周期[10-13]。采用USFOS 软件对“勘探二号”平台进行模态分析[10]，计算提取平台前9 阶的自振周期分别为一阶4.85 s、二阶4.58 s、三阶3.13 s、四阶1.55 s、五阶1.16 s、六阶0.87 s、七阶0.65 s、八阶0.41 s 及九阶0.31 s。图7(a)～图7(e)分别展示了USFOS 仿真分析结果与试验测试结果的对比。

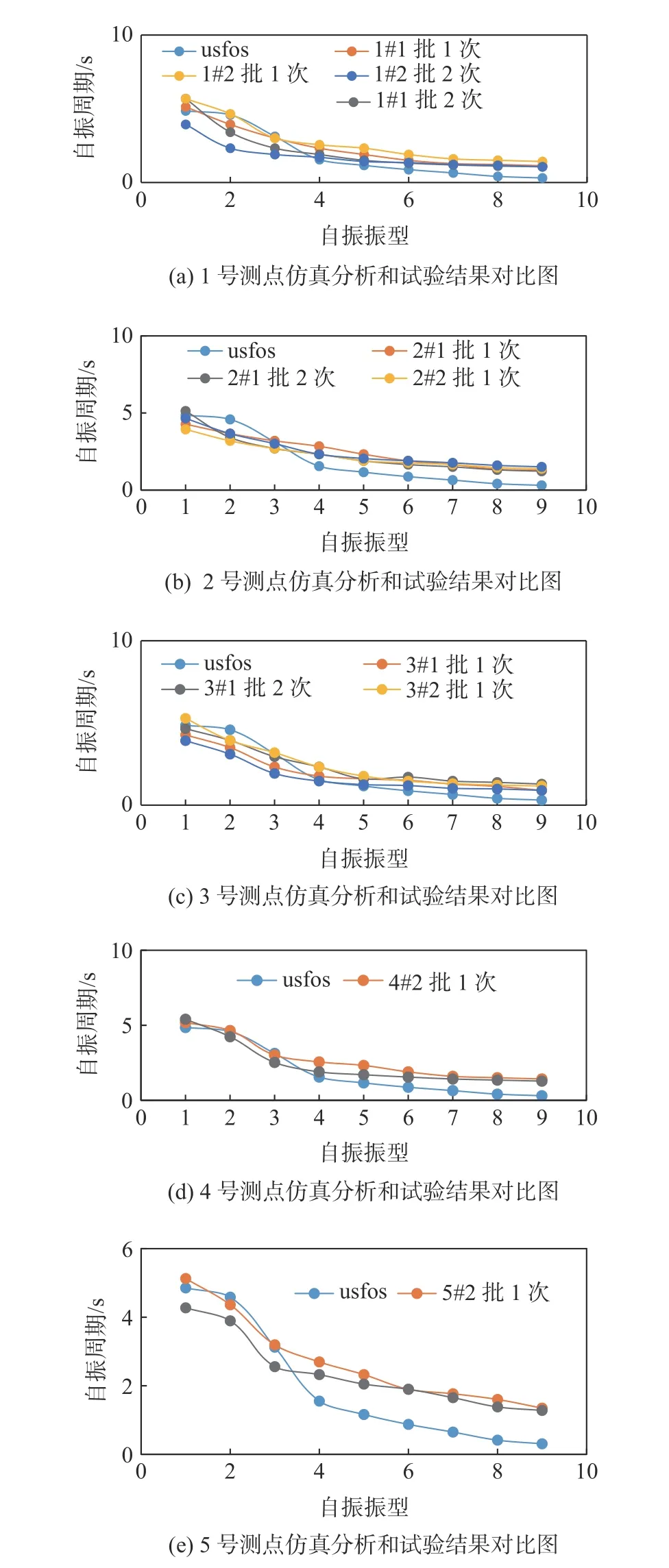
图7 1～5 号测点仿真分析和试验结果对比Fig.7 Comparison of simulation analysis and monitoring results for point 1～5

从图7(a)～图7(e)可以看出，平台仿真分析的前3 阶固有自振周期分别为4.85 s、4.58 s、3.13 s，现场测试的平台前3 阶固有自振周期分别为4.83 s、4.05 s、2.84 s，与仿真分析结果相对误差分别为0.59%、11.63%、9.08%，仿真模型计算的结果与测试结果基本一致。需要特别指出的是结构的第一、二和三振型都非常靠近。前三阶分别代表平台结构的整体振型。这测试结果验证了所建USFOS 仿真结构整体模型非常准确，能够反映出真实的结构动力特征。另外，第4 至9 阶自振周期也变化趋势一致，这5 阶振型主要为平台结构局部振型。也说明有限元仿真模型较为准确可靠，从而验证了仿真计算分析的准确性。

6 结论

本文以“勘探二号”自升式平台为研究对象，建立了平台数字仿真有限元模型，首次提出了建立在失效概率分析基础上，采用有限元仿真模型判断自升式平台的可靠性的计算方法；从而可以在平台作业中出现结构局部失效时，快速判断平台结构的可靠性，为平台继续生产作业提供可靠的技术依据。同时，利用有限元模型计算得到平台的固有周期与振型，并提出了以加速度传感器来测试平台结构振动特征及验证数字仿真模型的思路；完成了海上现场测试试验，验证了有限元仿真模型的准确性。取得的结论有：

（1）该项目的研究方法和结论为判断自升式平台的结构可靠性提供了一种量化判断方法，其结论可以运用于作业者的实际生产作业中。

（2）该项目发明了一种采用加速度传感器测试自升式平台自振频率或周期的方法；其测试结果可以与仿真计算的自振频率或周期进行对比分析；特别是前三阶结构主振型的对比分析，从而可以判定仿真模型的准确性。

（3）该项目的研究成果可以用于针对性平台的大数据库的建立，为将来的快速平台结构可靠性判断提供技术依据。

（4）针对自升式平台结构振动特征，基于加速度传感器设计了加速度传感器测试系统，能够较准确地测试自升式平台的自振周期。