西湖凹陷X 气田致密气储层测井评价及产能预测

王安龙，翁冬子，任培罡，吕 鹏，潘 潞，吕艾新，魏 锋

（1.中国石油化工股份有限公司上海海洋油气分公司勘探开发研究院，上海 200120；2.中石化华东石油工程有限公司科技发展分公司，江苏南京 210011）

研究区位于东海陆架盆地西湖凹陷，致密气藏埋深主体位于3 000～4 800 m，沉积亚相为三角洲平原、三角洲前缘和潮坪相。储集层岩性以中-细砂岩为主，含少量粉砂岩及含砾砂岩。储层孔隙度主要分布在7%～15%，渗透率主要分布在（0.3～50）×10−3μm2，整体属于低孔、中-低渗储层[1]。

研究区储层在测井识别时主要的难点：一是孔渗饱等定量解释参数精度偏低，不能满足研究和生产对参数的高精度要求，例如对渗透率的误差要控制在半个数量级内，这在致密及岩性复杂条件下常规方法很难达到；二是致密储层流体性质判断难。致密储层的岩性信号强，流体信号弱，很多高阻层出水，低电阻层产气，常造成测井解释与生产不符的问题；三是海上油气田单井产量要求较高，测井不仅要解释出气层，还要对储层有效性及产能做出判断。针对上述疑难问题，本文从研究区储层特点出发，从沉积相建模、神经网络预测流体性质及测井参数预测产能三个方面提供解决方法。

1 沉积相约束的测井模型

不同沉积相下的砂体由于沉积水动力条件不同，造成砂体的岩性、矿物成分、分选、粒度、孔喉结构等方面存在差异。例如，三角洲沉积体系中由陆向海岩性逐渐变细，潮坪相也表现为从中砂岩到细砂岩、到粉细砂岩变化（表1），不同岩性会有不同的孔渗关系（图1），不同的岩性也会导致油气充满度存在差异，进而影响饱和度参数；不同沉积相条件下的砂体岩性矿物成分不同（图2），造成岩石骨架密度变化，影响孔隙度；不同沉积相的砂岩分选性也不同（图3），分选性的好坏会影响储层的均质性，也间接影响储层的胶结程度[3]，进而影响有效孔隙度及渗透率。

图1 不同岩性孔隙度与渗透率关系图Fig.1 Relationship between porosity and permeability of different litholog

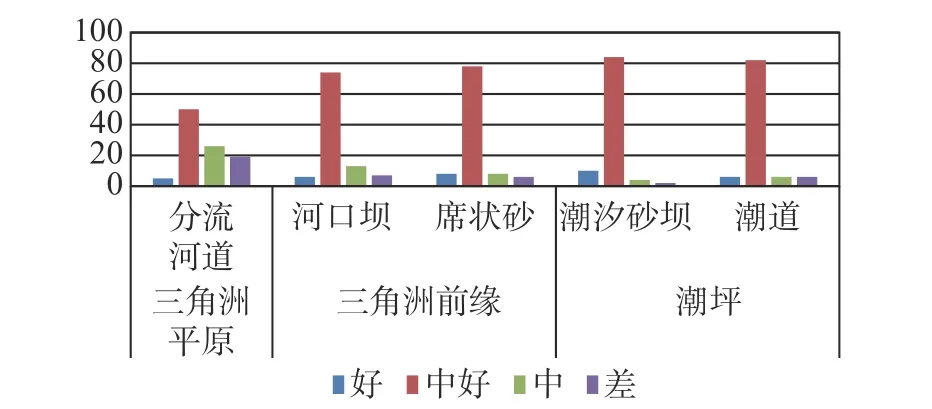
图3 不同沉积相的砂岩分选直方图Fig.3 Sandstone sorting histograms of different sedimentary facies

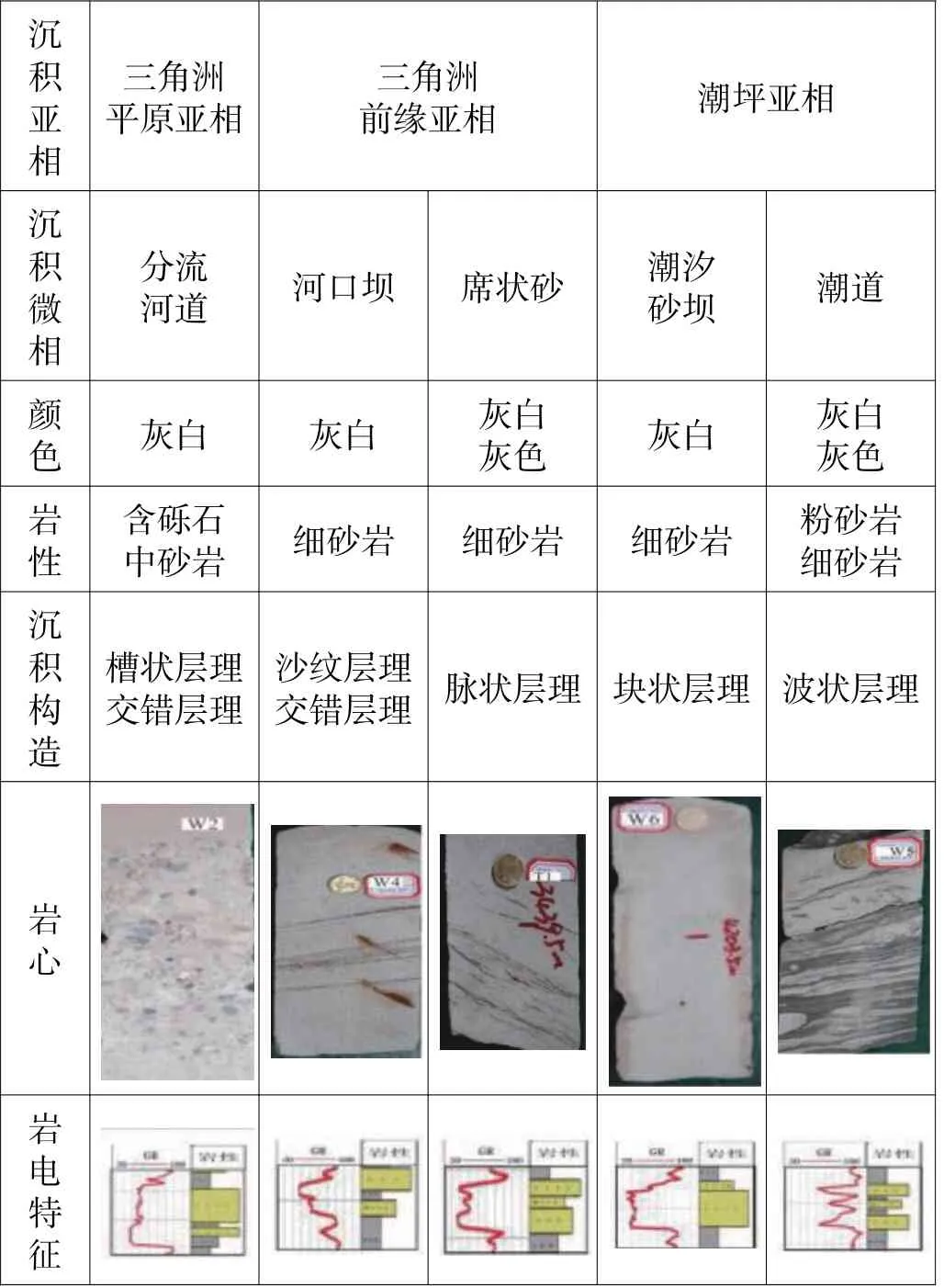
表1 不同沉积相的岩心及测井相特征表[2]Table 1 Core and logging facies characteristics of different sedimentary facies [2]

从上述分析可以得出，砂体的沉积环境不同会导致孔隙度、渗透率和饱和度参数存在较大差异。因此通过分沉积相类型方式建立测井解释模型和解释参数是一种反映储层特征、提高测井解释精度的途径[4-5]。

1.1 相控多元孔隙度模型

曲线敏感性分析表明研究区的声波时差、补偿密度及补偿中子测井曲线与孔隙度关系密切，其中声波时差相关性最高，其次是补偿密度曲线和补偿中子曲线（表2），可以采用三条曲线计算孔隙度。

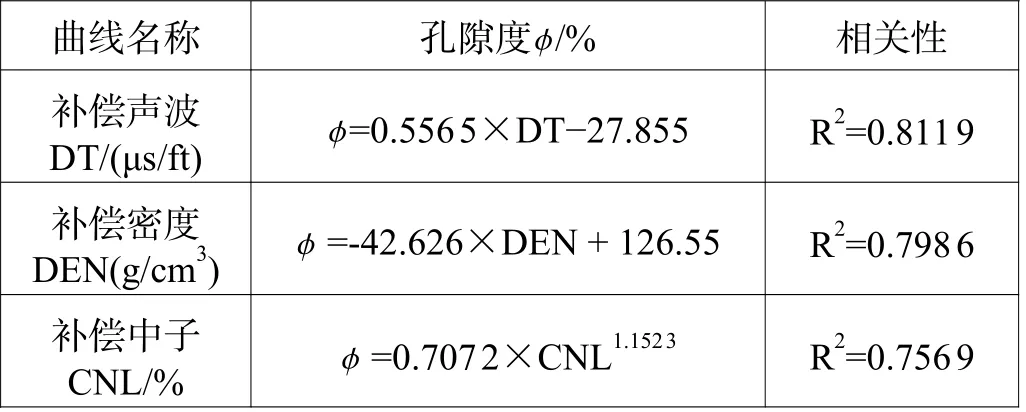
表2 三孔隙度测井公式表Table 2 Three porosity logging formula table

为进一步提高孔隙度解释精度，采用多元回归结合分沉积相的方式建立孔隙度模型。研究区目标层段砂体沉积亚相为三角洲平原相、前缘相、潮坪相，因不同沉积亚相的砂岩孔隙特征存在差异，分沉积亚相建立多参数模型进一步提高了模型的相关性[6]（表3）。

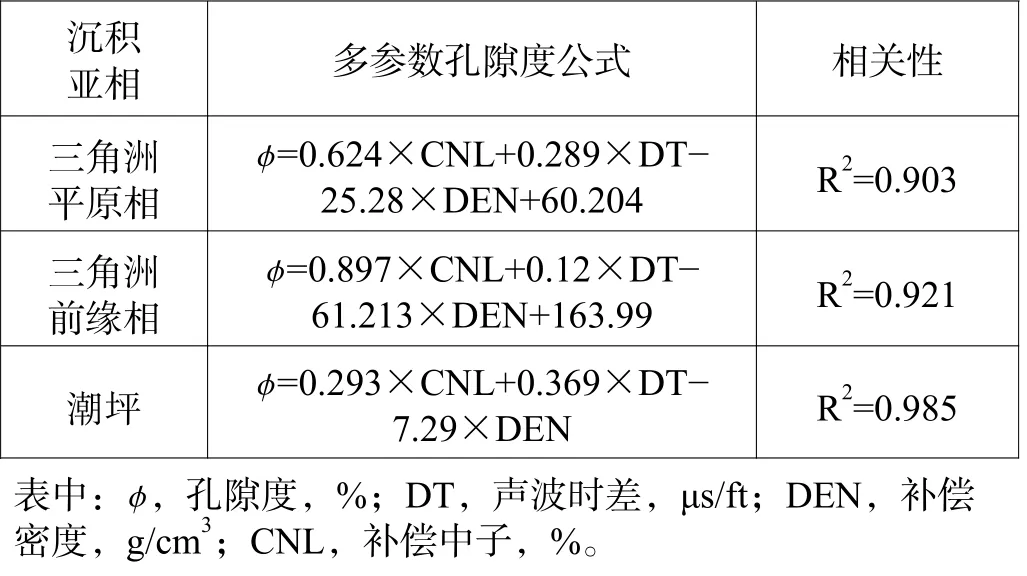
表3 不同沉积相条件下多参数孔隙度测井公式Table 3 Multi-parameter porosity logging formula under different sedimentary facies conditions

1.2 相控覆压渗透率模型

本次利用岩心物性实验资料结合覆压孔渗校正渗透率的方式建立精细解释模型。储层渗透率主要与储层孔隙度大小有直接关系，用其计算渗透率是业内通用做法。根据现有孔渗实验数据结合不同沉积亚相下孔渗相关性的差异，细分不同沉积亚相建立渗透率解释模型（表4）。

表4 不同沉积相下的渗透率公式Table 4 Permeability formulas for different sedimentary facies

上述岩心渗透率数据是在常温常压条件下实验所测，不能代表实际储层高温高压条件下的真实渗透率，压实作用越强，地下渗透率与地面渗透率差别越大。研究区埋深3 000～4 800 m，常压和超压层均有分布，地层压力在35～52 MPa 区间，根据相关统计表明，研究区储层渗透率如果不进行覆压校正，渗透率平均绝对误差5.26×10−3μm2，平均相对误差345%。

因此在上述沉积亚相计算渗透率的基础上开展覆压校正，能更好反应地下储层的渗流能力。从图4 及表5 可以看出，常压渗透率校正到覆压条件的校正模型是分段的，大体可以分中高孔渗、中低孔渗及特低孔渗三种，孔渗性差的储层需要校正的量相对越大，这也反应出压实作用对渗透率影响大[7]。

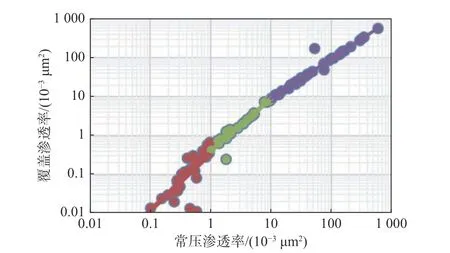
图4 渗透率三段式覆压校正图Fig.4 Three-stage overburden pressure correction diagram of permeability

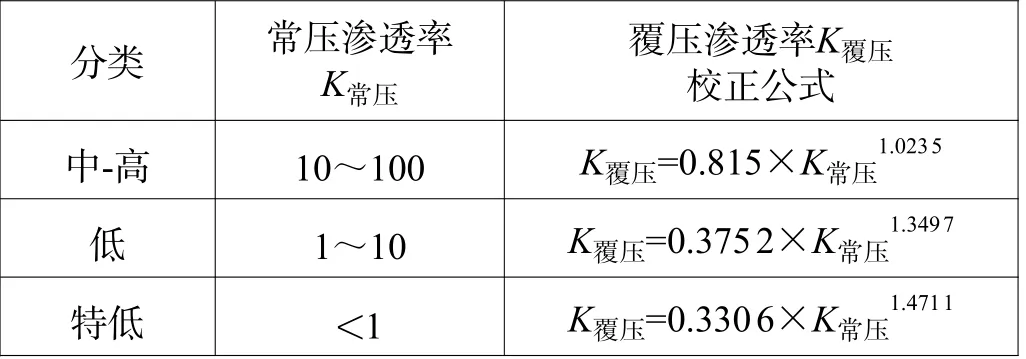
表5 常压与覆压渗透率公式表Table 5 Permeability formulas of normal pressure and overburden pressure

测井计算时根据表4 中分沉积相计算得到的常压渗透率K常压，再按照表5 不同K常压区间开展渗透率的覆压校正，得到校正后的覆压渗透率。

1.3 相控含水饱和度模型

从本区已有储层岩石矿物成分资料来看，8 口井105 个砂岩样品的黏土分布范围1.2%～32.8%。平均7.6%； 8 口井94 个黏土样品中伊/蒙混层分布范围1.0%～92.0%。平均22%，导电黏土成分较高，因此在计算含水饱和度时需要考虑泥质附加导电性的影响。

西门杜公式是流体加泥质导电的双导电模型，当泥质的矿物成分伊蒙混层比例高导致泥质导电能力较强时，西门杜公式更适用。

式中：Sw，含水饱和度，小数； φ，地层孔隙度，小数；Rw，地层水电阻率，Ω·m；Rt，地层电阻率，Ω·m；Vsh，泥质含量，小数；Rsh，泥质电阻率，Ω·m；m，胶结指数，常数；n，饱和度指数，常数。

在选择合适的饱和度解释模型基础上，在岩电参数上开展精细分类，依照不同沉积相细分岩电参数（表6）。从岩电参数可以看出，不同沉积相下的砂体岩电参数存在明显差异，分沉积相建立岩电参数能更好地反应不同砂岩的特性。

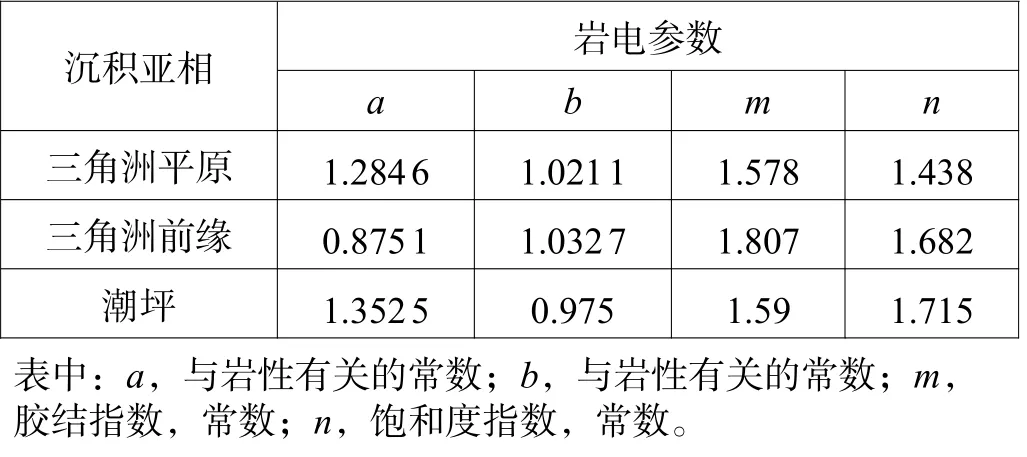
表6 不同沉积相条件下岩电参数统计Table 6 Statistical of rock electrical parameters under different sedimentary facies conditions

1.4 相控束缚水饱和度模型

束缚水饱和度是流体-岩石之间综合特性的反映，主要取决于岩石孔隙毛细管力的大小与岩石对流体的润湿性。孔隙度和渗透率是能间接反映束缚水饱和度大小的岩石物性参数，孔隙度小的岩石，其孔隙度结构一般较为复杂，孔隙度空间小，喉道细，因而能束缚较多的水，形成高束缚水饱和度。采用6 口井的核磁共振实验资料，建立束缚水饱和度模型。

核磁共振实验表明，束缚水饱和度与渗透率和孔隙度关系密切，其中与渗透率相关性最好，与孔隙度相关性其次。 通过上述影响束缚水的因素分析，采用渗孔比建立束缚水饱和度模型。同时根据沉积相差异，采用分沉积相建立砂岩束缚水饱和度模型（表7）。

表7 不同沉积相束缚水饱和度模型统计表Table 7 Statistical table of bound water saturation models of different sedimentary facies

1.5 精度验证

以X 井为例，从图5 中可以看出利用文中的方法计算的孔隙度、渗透率和含水饱和度与岩心孔隙度、渗透率和密闭取心含水饱和度吻合性很好，证明文中的方法能有效反应储层，提高储层参数的精度。

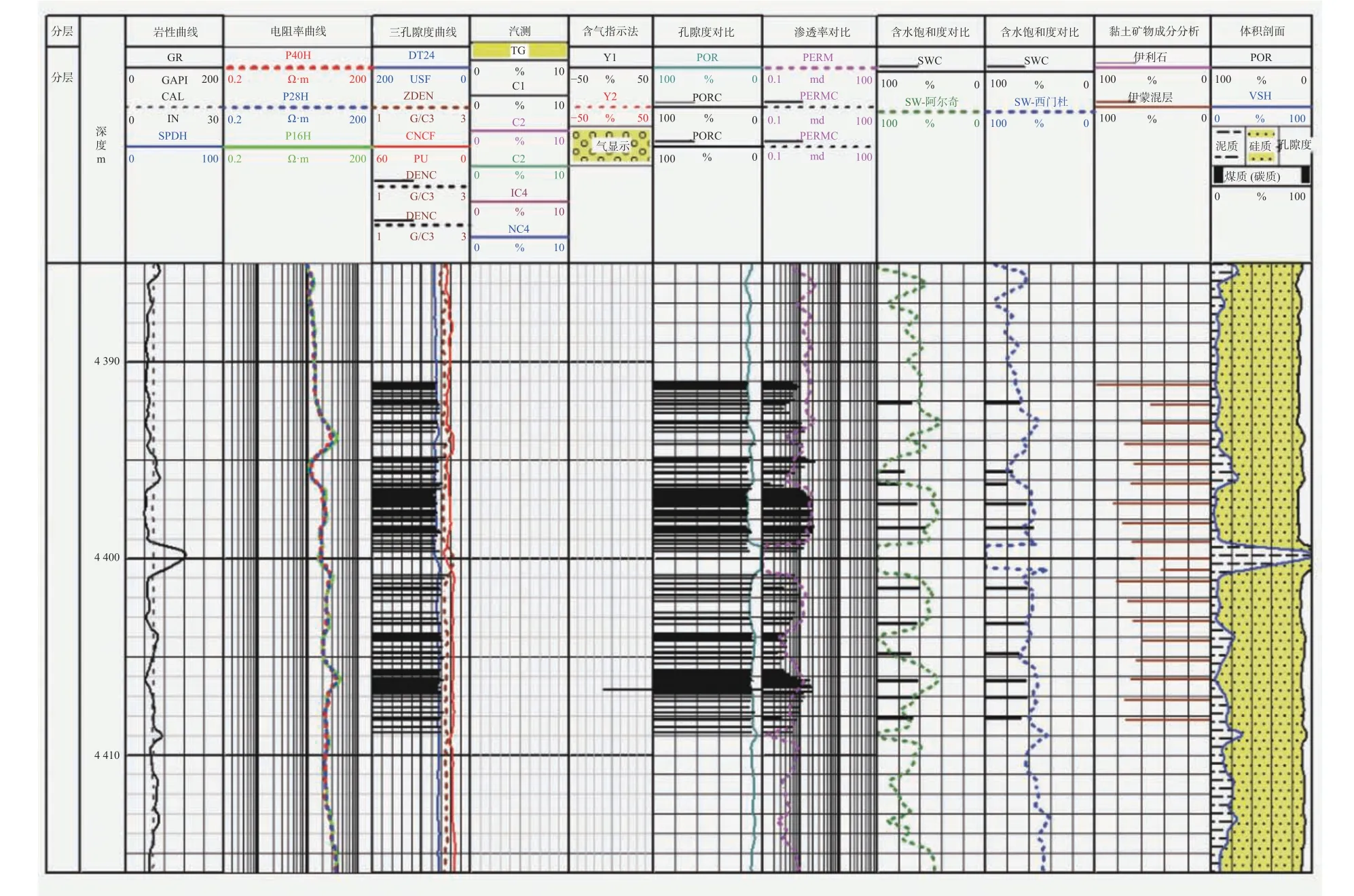
图5 X 井测井解释孔渗饱与岩心分析值对比图Fig.5 The comparison between well logging interpretation porosity, permeability and saturation and core analysis value in well X

2 神经网络法判别流体性质

人工神经网络有较强的抗干扰能力和非线性表达能力，其网络由神经元及神经元之间的连接权组成，它包括了输入层、隐藏层和输出层，属于由正向传播和反向传播组成的有导师的学习算法(误差反向传播算法)，它通过修改神经元之间的连接权得到期望的输出。神经网络技术对于已知存在某种潜质的联系但又无法用确切方程或算法表达的求解问题，有其独到之处。利用神经网络进行油气层定性预测，只要能建立一个良好的具有典型特征的测井学习样本，就可以用来处理一个测井问题。它可以避免在建立测井解释中模型所带来的复杂性，直接通过学习样本，建立测井信息和所求目标之间的关系[8-9]。

以标准化和归一化的自然伽马、声波、中子、密度及深电阻率曲线数据作为神经网络输入层，隐藏层采用3 层、12 节点模式（图6），输出层分为1 类（油气层）、2 类（气水同层）、3 类（水层）、4 类（干层）及5 类（泥岩）5 类的模式，利用经测试的、典型且具有广泛性的油气层、气水层、水层、干层及泥岩层数据构建的样本虚拟井作为神经网络学习样本（图7），利用建立起的学习结果对未知的储层进行预测识别。以Z 井为例，利用神经网络预测，从图8第4 道预测结果看，首先对储层与非储层的划分，砂泥岩储层的划分与常规测井曲线保持一致，划分结果较为准确（泥岩层为绿色区域）；对储层的流体类型预测，砂岩层段（GR 曲线黄色段）神经网络预测结果为1 类气层（第4 道蓝色区域），试油结果为日产气36.9×104m3/d，油121.8 m3/d，预测结果与试油吻合。

图6 神经网络结构模式图Fig.6 Neural network structure pattern diagram

图7 利用神经网络建立虚拟井图Fig.7 Virtual well diagram established using neural network

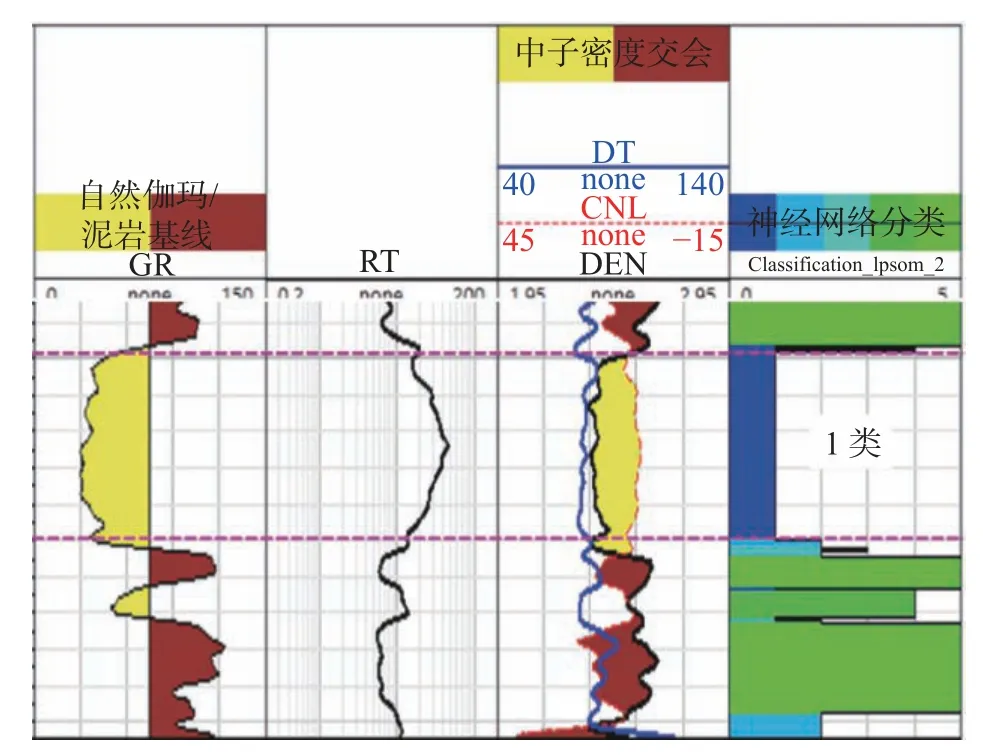
图8 Z 井神经网络预测流体性质成果图Fig.8 Neural network prediction results of fluid properties of Well Z

3 产能预测

在油田开发过程中，油气储层的生产能力主要受储层因素及工程因素影响，在同一区块可认为工程因素是相对不变的，因此决定产能的主要因素是储层因素。本研究通过产能指数反应储层产能大小。根据试油资料，获取了生产压差、油气层厚度和产量，进而计算了油气层产能指数PI（单位生产压差、单位油气层厚度和单位时间的油气层产量）[10-11]，见式（2）。

式中：PI为油气层产能指数，104m3/（m·MPa·d）；Q为日产量，104m3/d；h为有效厚度，m；Ps为生产压差，MPa。

根据6 口探井9 个试油层位统计，每米采油指数变化为0.01～4.35，结合储层分类，把油气储层产能的大小分为高、中-高、低产和无产能4 个等级（表8）。

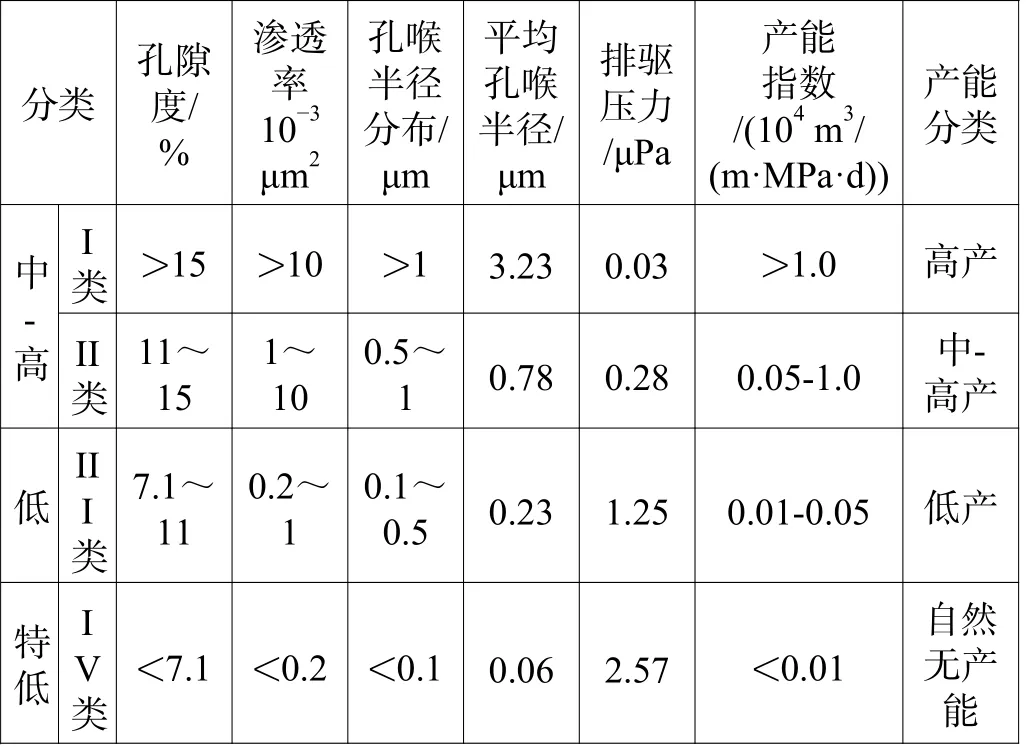
表8 压汞储层分类表Table 8 Classification of reservoirs using mercury intrusion method

经过分析，气层产能指数与储层孔隙度、渗透率及含气饱和度具有相关性，通过建立综合物性指数（K/ φ）与饱和度（So）乘积建立产能预测模型（式（3）），拟合后相关性得到明显提高。本区视产能指数的计算公式为：

式中：K为空气渗透率，10−3μm2；φ为孔隙度，%；PI视为视产能指数，104m3/（m·MPa·d）；So为含油气饱和度，%。

以Y 井为例，通过计算储层段平均视产能指数1.1×104m3/(m·MPa·d)，根据本井实际测试资料，该层测试厚度3.6 m，生产压差为6.07 MPa，利用视产能指数预测产能为24.0×104m3/d，实际测试日产气量25.4×104m3/d，两者吻合性高；对11 口井预测与实际产能对比，平均相对误差小于15%（表9），表明建立的产能指数预测模型在本区有较好的适用性，能够起到预测产能的作用。

表9 11 口井预测产能与实际产能对比表Table 9 Comparison of predicted production capacity and actual production capacity of 11 wells

4 结论

（1）在缺少特殊测井资料的情况下，通过常规测井资料精细评价致密储层难度大，但通过地球物理测井与沉积相结合，可以精细地刻画储层，建立合理解释参数。

（2）致密储层流体性质的准确判别受岩性影响很大，通过对流体敏感曲线的有效利用，结合神经网络算法，能够为一些疑难层及储层有效性的判断提供依据。

（3）海上油气田对经济性要求较高，在射孔层选择上更加慎重，测井不仅能给出解释结论，还能提供产能估算结果，既拓宽了测井资料的应用范围，也提升了测井资料的价值。