解一元线性同余式组的一个新算法
2024-01-04谢照林
谢照林
(美国布鲁克斯自动化公司,加州 佛利蒙市 94538)
0 引 言
一元线性同余式组是数论的一个组成部分。早在公元5世纪,中国的数学著作《孙子算经》就提出了一个“物不知数”问题:“有物不知其数,三三数之剩二,五五数之剩三,七七数之剩二。问物几何?”即,一个整数除以三余二,除以五余三,除以七余二,求这个整数。这个问题用现代数学语言可以表达为
x=2(mod 3),x=3(mod 5),x=2(mod 7),
求x=?
孙子的答案为x=2*70+3*21+2*15-2*105=23,用现代的同余式表达为x≡23(mod 105)。
1247年,宋朝数学家秦九韶在《数书九章》的《大衍类》中对“物不知数” 问题作出了完整系统的解答[1-8]。在国外,从6世纪到19世纪诸多印度和欧洲的科学家都提出了对同余式组的算法[9-10]。1801年,德国科学家高斯(Carl Friedrich Gauss) 提出了一个和秦九韶一致的算法,这是欧洲最早的完整系统算法[11]。1852年,英国传教士伟烈亚力(Alexander Wylie)把《数书九章》翻译成英文[12],它很快又被翻译成德文和法文,并在西方广泛传播。19 世纪末20世纪初,西方国家把秦九韶和高斯对一元线性同余式组的算法命名为中国余数定理。中国余数定理具有极高的理论和实用价值,已成为解一元线性同余式组算法的经典,本文称它为经典算法,并将在第1节对其进行简要介绍。
近年来,国内外学者对一元线性同余式组问题的研究还在持续不断[13-19],研究的重点是它在各个领域的应用。除此之外,在互联网上对于扩展的同余式或同余式组的各种不同解法的讨论也很活跃,但是有关中国余数定理提出的基本的一元线性同余式组问题则无论在互联网上或是出版文献上都极少见到有人提出新的解法。偶尔见到的有穷举法、解不定方程法、化为相同除数法,等等。这些解法扩大了人们的思路,也各有其适用的场合,不足的是求解过程往往因题而异,依赖人工判断,也未见到这些解法各自的可用于计算机计算的通用算法。
经典算法的计算步骤清晰且通用,在它形成的年代计算机尚未出现,但是它却成为一个现成的可用于计算机计算的通用算法。本文提出解一元线性同余式组新算法的初衷,是想探讨能否在经典算法之外找出另一种更高效的可用于计算机计算的通用算法。在现在这样一个需要快速处理大量大数值数据的时代,多一种算法供使用者选择总是有益无害的。
本文提出的新算法的思路和经典算法完全不同,在文中被称为杠杆算法。计算机对比计算的结果表明,与经典算法相比,杠杆算法可以处理数值更大的数据以及具有更快的运算速度。尽管如此,杠杆算法也仅仅是一个算法,而不是一个理论,完全无法与经典算法相比拟,可以把它看作一个不同的解题计算工具。
1 一元线性同余式组的经典算法(中国余数定理)
1) 经典算法(中国余数定理)问题的提出:
给定同余式组x≡a1(modm1),x≡a2(modm2),…,x≡an(modmn),其中,m1,m2,m3,…,mn都是互质的(互为质数,它们的最大公约数为1),求解x。
2) 解题步骤可归纳如下:
① 计算乘积M=m1m2m3…mn;
② 对于i=1,2,…,n,依次计算ui=M/mi=m1m2…mi-1mi+1…mn;

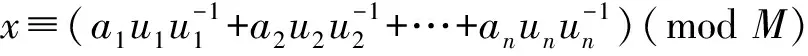

2 一元线性同余式组的新算法(杠杆算法)
给定同余式组x≡a1(modm1),x≡a2(modm2),…,x≡an(modmn),其中,m1,m2,m3,…,mn都是互质的,求解x。以下称n为该组的规模。杠杆算法的解题步骤是先解两个同余式,然后把它的结果与第3个同余式求解,依此类推直至n个同余式都被用到。
2.1 两个同余式的求解
x≡a1(modm1) 可以写为x=q1m1+a1。其中,q1是x除以m1的商,a1为余数,m1为模数。x≡a2(modm2) 可以写为x=q2m2+a2。其中,q2是x除以m2的商,a2为余数,m2为模数。
约定两个同余式中模数大的同余式称为x≡a2(modm2),另一个称为x≡a1(modm1),两式相减可得
q2m2+a2-a1=q1m1。
(1)
式(1)表明,(q2m2+a2-a1) 必须是m1的整数倍,可表达为
Δ=(q2m2+a2-a1) modm1=0。
(2)
求解目标1是找出满足Δ=0 的q2值,则x=q2m2+a2就是求得的解。
模数运算具有如下性质[15-16]:
(A+B) modC=(AmodC+BmodC) modC,
(A*B) modC=(AmodC*BmodC) modC,
可以看出,只要括号外有modC,那么对于括号内的各项,modC可以任意增减。因此,有
Δ= (q2m2+a2-a1) modm1=
(q2(m2modm1)+(a2-a1) modm1)modm1。
(3)
当q2=0时,式(3)成为Δq2=0=(a2-a1)modm1,这是Δ的初值,可以用符号Δ0把它定义为
Δ0=(a2-a1) modm1。
(4)
当q2=1时,Δq2=1比Δq2=0多一项m2modm1,这是q2从0变为1时Δ的增量,由于q2的变化量是1,Δ的增量也就是函数Δ(q2)在起点的差分。由于Δ(q2) 是线性函数,它也是在q2全域各点的差分。可以用符号δΔ把它定义为
δΔ=m2modm1,
(5)
由此,式(3)又可写为
Δ=(q2*δΔ+Δ0) modm1。
(6)
参数a1,m1,a2,m2是一组同余式的固有参数。Δ0和δΔ包含了这4个参数,所以Δ0和δΔ就成为这一组同余式的特征参数,是杠杆算法的出发点。求解目标2是找出q2值使式(7)成立,
Δ=(q2*δΔ+Δ0) modm1= 0。
(7)
得到满足条件的q2值的方法有两种:
1) 逐一试探q2=1,2,3,…,直到式(7)成立。
2) 式(7)等价于
q2*δΔ+Δ0=km1,
(8)
式中:k是一个最小可能的正整数。
于是,可以得到
q2= (km1-Δ0)/δΔ。
(9)
逐一试探k=1,2,3,…,直到
α=(km1-Δ0) modδΔ=0,
(10)
把找到的k值代入式(9),就可以求出q2。
由于δΔ=m2modm1,所以δΔ
2.2 三个以上同余式的求解
无论用q2试探还是k试探,已经得到x=q2m2+a2。按照中国余数定理,这个同余数是对于模数乘积m1m2而言的,即
x=(q2m2+a2) (mod (m1m2))。
如果使用新变量
a2=(q2m2+a2),m2=(m1m2),
(11)
把新加入的第3个同余式的下标由3改为1,即
a1=a3,m1=m3,
(12)
那么,可以得到以下两个新的同余式
x≡a1(modm1),x≡a2(modm2)。
(13)
在解出3个同余式(13)以后,重复上述式(11)~式(13)的方法,总共进行n-1次就可以完成n个同余式的求解。
2.3 杠杆算法(减少试探次数)
k试探比q2试探高效,但随着模数数值的增大,k试探也越来越耗时,必须找到加速k试探的途径。回顾式(10),如同处理由Δ表达式得出δΔ一样,可以得到
δα=m1modδΔ。
定义Δ00=Δ0modδΔ,则式(10) 可以写为
α=(k*δα-Δ00) modδΔ=0,
(14)
也就是(k*δα-Δ00) 必须是δΔ的整数倍,这里需要的是最小的整数倍。为此,
k*δα-Δ00=p*δΔ,
式中:p是一个最小可能的正整数。故
k=(p*δΔ+Δ00)/δα,
(15)
即以p来求k。
δΔ/δα>1,所以任何p值都能产生一个比它大的k值。p和k的关系又是一个杠杆,这是第2级杠杆。
同理,定义
β=(p*δΔ+Δ00) modδα,
(16)
可得
δβ=δΔmodδα,
定义
Δ000=Δ00modδα。
设定求解目标:β=0。由此得到第3级杠杆
p=(s*δα-Δ000)/δβ,
(17)
式中:s是一个最小可能的正整数。这是以s求p。
同理,可得第4级杠杆
s=(t*δβ+Δ0000)/δγ,
(18)
式中:t是一个最小可能的正整数。这是以t求s。
2.4 杠杆迭代(彻底免除试探)
1) 迭代的形式:汇总以上用过的各个表达式,如表1 所示。

表1 各级杠杆的表达形式
由表1 可以看出,各级杠杆表达式的结构是相同的,可以用一个通用的形式来概括,如表2 所示。

表2 杠杆迭代的通用形式
表2 中Δi的下标i代表迭代次序[i]。在迭代[1]中Δi是Δ0,在迭代[2]中Δi是Δ00,依此类推; 符号Δi等效于Δ的下标为i个0,每次迭代中它都是该次迭代运算的初值。表2 中各表达式的形式更便于进行迭代运算,称这样的迭代为杠杆迭代。其中,第1步是正向迭代:按照[0],[1],[2],[3],…的顺序自上而下计算第1列和第2列; 第2步是反向迭代:按照相反次序自下而上计算第3列,直到算出k1。对照表1 和表2 可知,k1就是q2。
2) 迭代的实例:在计算机上进行实例计算所得结果为
Solve(4 801,9 739),(5 107,10 009):
[1]:D0=306,dEps0=10 009,dEps1=9 739,dEps2=270,bSignOfD=1
[2]:D0=36,dEps0=9 739,dEps1=270,dEps2=19,bSignOfD=0
[3]:D0=17,dEps0=270,dEps1=19,dEps2=4,bSignOfD=1
[4]:D0=1,dEps0=19,dEps1=4,dEps2=3,bSignOfD=0
[5]:D0=1,dEps0=4,dEps1=3,dEps2=1,bSignOfD=1
dEps2=1,sosetk[6]=1
[5R]:k[6]=1,k=2
[4R]:k[5]=2,k=3
[3R]:k[4]=3,k=10
[2R]:k[3]=10,k=144
[1R]:k[2]=144,k=5 193
Finally,k=144,q2=5 193,x=51 981 844
Thecongruenceisx=51 981 844 (mod97 477 651)
其中,方括号里的数字代表迭代的次序; 字母R代表反向;D0在各次迭代中分别代表Δ0,Δ00,Δ000,Δ0000,…;dEps0,dEp1s,dEps2 在迭代[2]中代表δε0,δε1和 δε2,在迭代[3]中代表δε1,δε2和 δε3,依此类推; 布尔变量bSignOfD代表计算ki值时Δi应有的正负号; 1代表应该用负号,0代表应该用正号。从该实例可以看出,5次迭代计算就得到 k=144,q2=5 193,比k试探,尤其是比q2试探,效率提高了很多倍。
3) 正向迭代结束的条件:在正向的每一次迭代中都有对δεi=δεi-2modδεi-1的计算,所以,当δεi= 1时,正向迭代就完成了。理由如下:
表2 的每一行都有ki=(ki+1*δεi-1±Δi)/δεi,当δεi= 1时,取任何整数ki+1都可以得到ki为整数。这里要取最小的正整数ki+1=1。所以,正向迭代结束的条件就是δεi=1。此时,取ki+1=1。
下面讨论δεi= 1 是否一定会出现。
表2 中正向迭代[2]是从δε2= δε0modδε1开始的,也就是从δε2= m1mod(m2modm1) 开始的。其后δε3= δε1modδε2就是δε3= (m2modm1)mod(m1mod(m2modm1)),依此类推。这就是m2和m1的辗转相除,即求m2和 m1的最大公约数(GCD)的过程。而m2和 m1是互质的,即它们的GCD是1。因此,δεi= 1一定会出现,至于δεi= 1在第几次迭代中出现,取决于题目数据m2和 m1的值。
2.5 杠杆算法的步骤
杠杆算法用到两层迭代。外层迭代是先解两个同余式,然后其结果又和第3个同余式一起按照解两个同余式的过程求解,其结果又和第4个同余式一起求解,依此类推,总共需要n-1次,n是同余式组的规模。内层迭代就是杠杆迭代,它是在每一次外层迭代中解两个同余式的过程中都要使用的。设每一次外层迭代的已知数据是 (a1,m1),(a2,m2),杠杆算法的解题步骤如下:
1) 对于规模在2以上的同余式组按照模数值从大到小进行排序。这个排序对于每一道题目只做一次,目的是使各次外层迭代的运算时间尽可能均衡,从而减少总的运算时间。气泡排序就是常见的有效算法。当然,是否做模数排序对计算结果没有影响。
2) 计算常数δε0=m1,Δ0=(a2-a1)modm1,δε1= m2modm1。
3) 按照表2逐次正向迭代计算Δi和δεi。
4) 当δεi= 1,令ki+1= 1,开始反向迭代,直到算出k1。这个k1是q2。
5) 计算a2=q2m2+ a2,m2=m1m2。把下一个同余式命名为(a1,m1),进入下一次外层迭代的步骤2)。
3 经典算法和杠杆算法的比较
3.1 可处理的数值范围的比较
一个64位(二进制位数)计算机能接受的最大正整数是Z=9 223 372 036 854 775 807,即十进制19位数。


表3 杠杆算法可处理的最大数值是经典算法可处理最大数值的倍数
3.2 运算时间的比较
解一道一元线性同余式组问题的运算时间是微秒级的,在通常条件下无法直接测得。在以下的实例中每道题都重复计算了4 000万次,然后算出运算一次的平均时间,计算结果如图1 所示。

(a) 运算时间随最大模数值的变化
图1(a) 中每一个算例都是一个规模为3的同余式组。最大模数值是指3个同余式中最大的模数值。由图1(a) 可知,运算时间随最大模数值的增大而增大。但是,对于最大模数值的跨度101~1 000 003 而言,增长率可视为0。杠杆算法运算时间的平均值是0.87 μs,比经典算法的1.33 μs减少35%。由图1(b)可知,杠杆算法运算时间的平均值是1.53 μs,比经典算法的2.08 μs减少27%。
以上每一例杠杆算法运算时间都已经包括了模数排序的运算时间。
4 结束语
1) 单纯从求一元线性同余式组解题答案的角度来看,杠杆算法和经典算法是两个并行的算法,二者殊途同归。二者计算任何题目所得答案完全相同。但是,从数学学科的角度来看,经典算法具有严谨的数学思维,是数学殿堂中的一件瑰宝,而杠杆算法只作为计算工具。
2) 与经典算法相比,在相同的计算机条件下,杠杆算法可以处理数值更大的数据以及具有更短的运算时间。

4) 今后可以尝试在解扩展的同余式和同余式组问题方面进行高效的计算机算法的探讨。
