EBSM电子束扫描多极靴偏转线圈的多目标优化设计

张化斌,马贵春,郑俊旺,郭思博,王 磊,刘 洋

(中北大学 航空宇航学院,山西 太原 030051)

0 引 言

电子束选区熔化增材制造技术(Electron Beam Selective Melting,EBSM)具有成形速度快、能量利用率高、成形效率高等特点,可轻松成形具有复杂形状的高性能金属零部件[1-4],因此被广泛地运用于航空航天、生物医疗等领域[5-7]。但是,电子束偏转的精确控制程度会影响复杂零件成型的质量。由于电子束的偏转扫描控制是非接触式的,电子束的惯性和质量几乎可以忽略,通过控制电子束运动空间中电磁场的大小和方向就可以实现对电子束运动轨迹的控制。偏转扫描线圈所产生电磁场的均匀性是影响电子束偏转精度的重要因素,因此,使用电磁场均匀性差的线圈难以实现电子束的精确控制[8]。

针对上述问题,学者们对电子束偏转线圈进行一些研究。一些著名电子束加工设备研制单位如CVE(Cambridge Vacuum Engineering)、TWI(The Welding Institute)、PTR(Pulsed Technologies Research)等[9]均对电子束偏转扫描技术进行了深入研究,其中德国SST所研制的电子束偏转扫描控制系统的频率已经达到了200 kHz。路开通等[10]基于亥姆霍兹线圈设计偏转线圈,其频率达30 kHz。张伟等[11]基于亥姆霍兹线圈设计了偏转线圈,其扫描速度可达3 500 m/s,扫描范围最大为350 mm×350 mm。赵攀峰等[12]也基于亥姆霍兹线圈设计了偏转线圈,其扫描范围可达350 mm×350 mm,扫描速度为7 000 m/s。杨波等[13]设计了以铁氧体为磁芯材料的十二极靴偏转线圈,其频率达100 kHz以上。相关文献均对EBSM系统的电子束扫描偏转线圈的设计提供了参考,但亥姆霍兹线圈的体积较大,不便于配置磁芯,且中心场强较弱,难以满足EBSM系统大角度偏转的要求。多极靴结构线圈虽然加工精度要求低、中心场强较大,但是其磁场均匀性较差,不利于实现电子束偏转的精确控制。目前,针对EBSM扫描偏转线圈的多极靴结构磁场强度分析与多目标优化设计的已公开研究较少。

本文将多极靴线圈结构的极靴数和磁芯类型作为变量,设计多极靴线圈磁感应强度正交仿真试验,阐明试验的设计方案及结果,对线圈中心磁感应强度、距线圈中心2.5 mm和5 mm范围内磁感应强度的变化率进行对比分析。通过极差分析法更加直观地分析单因素对于线圈中心磁感应强度、距线圈中心2.5 mm和5 mm范围内磁感应强度变化率的影响程度及其变化趋势,进一步采用MOEA/D算法对此问题进行优化求解,并得到使线圈中心磁感应强度较大、磁场较均匀的结构参数。

1 数学模型

1.1 磁偏转理论

EBSM设备所使用的电子束偏转系统,通常以较小的偏转角度工作,电子束以恒定的速度进入均匀磁场,在洛伦兹力作用下做圆周运动,如图1 所示。

图1 电子束运动轨迹图

根据电磁理论可得

(1)

式中:R为圆周运动半径;m为电子质量;v为电子运动速度;e为电子电荷;B为磁感应强度;Va为电子枪的加速电压;η为电子荷质比。

电子束离开均匀场后的偏转角δ满足

(2)

由电磁理论可知,磁感应强度与线圈电流成正比,即

B=kI,

(3)

式中:k为与线圈相关的常数;I为线圈电流。

假设线圈所产生的磁场宽度与线圈自身高度h一致,可得

(4)

对于EBSM成型系统而言,电子枪加速电压Va通常是固定值,偏转线圈在设计完成后其高度h自身相关常数k也已确定,因此,系统将通过控制线圈中的电流从而控制电子束的偏转角δ。

1.2 线圈结构

多极靴线圈结构如图2 所示,其能够在紧凑的空间内布置大量的对称线圈,从而提高中心磁场的均匀度和场强,且能通过将线圈骨架替换为软磁材料磁芯来进一步提升中心场强。多极靴线圈的结构形式较多,下面将针对四极靴、八极靴、十二极靴、十六极靴以及二十极靴的线圈中心磁场强度和距线圈中心2.5 mm、5 mm范围内磁场均匀度设计正交仿真实验,对多极靴偏转线圈进行三维电磁场分析。

图2 多极靴线圈结构示意图

2 正交仿真试验

2.1 正交试验设计

根据极靴数量和磁芯类型设计正交试验,探究极靴数量及有无磁芯对多极靴线圈磁感应强度和磁场均匀性的影响规律,因素水平如表1 所示,正交试验方案如表2 所示。

表1 正交试验因素水平

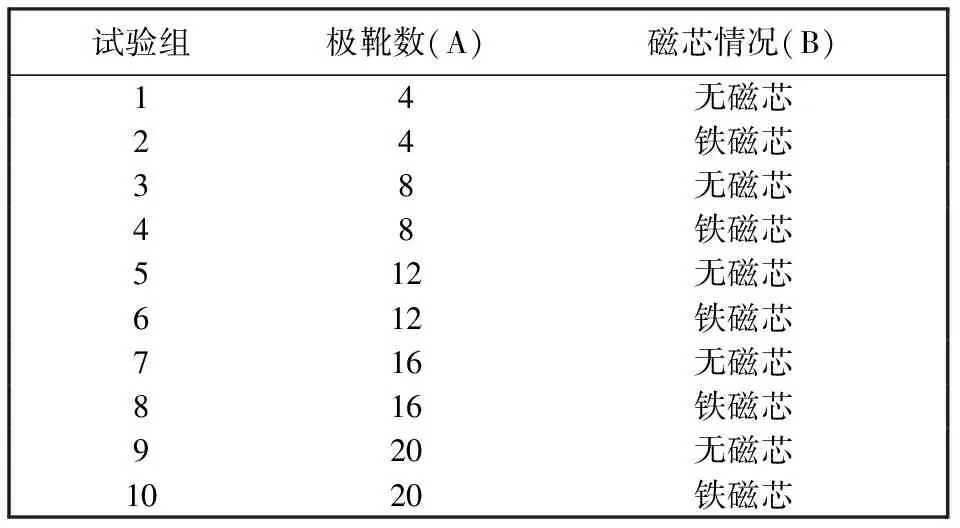
表2 正交方案

2.2 仿真实验

2.2.1 模型建立

对多极靴偏转线圈建模,如图3 所示,线圈内径90 mm,外径110 mm,极靴高度10 mm,磁芯高度30 mm。定义磁芯材料为铁(相对磁导率1 000)或真空(相对磁导率1,用作线圈骨架)。磁芯每极靴上绕制的线圈均定为宽度5 mm,厚度2 mm,匝数32匝,电流设置为单位电流1 A。磁芯中心位于聚焦线圈中心Z轴+155 mm位置上。

图3 不同极靴数偏转线圈模型

2.2.2 仿真设置

在完成对仿真模型的建模后,还需要对环境及边界条件、仿真模型的网格划分和求解器的参数进行设置。由于EBSM系统在工作时,系统内部处于高度真空状态,因此,在仿真中对环境材料定义为真空,相对磁导率为1。采用六面体网格划分,并对线圈网格作更进一步的调整以增加网格密度。

3 仿真试验结果与极差分析

3.1 试验结果

在试验结果的后处理中,选定Z轴方向为剖切平面法线,使剖切面经过线圈中心,并将三维的磁感应强度分布云与剖切面相交,可获得剖面内的磁感应强度分布情况。图4 中(a)、(b)、(c)、(d)、(e)分别为四极靴无磁芯、八极靴无磁芯、十二极靴无磁芯、十六极靴无磁芯、二十极靴无磁芯线圈的磁感应强度分布情况,有磁芯的情况见图5。可以看到,随着极靴数的增加,无磁芯与有磁芯线圈的磁感应分布均匀度、对称度都有很大的提高。同时,在有磁芯存在的情况下,磁感应强度分布更集中于磁芯与线圈内部,向线圈外的漏磁更少。

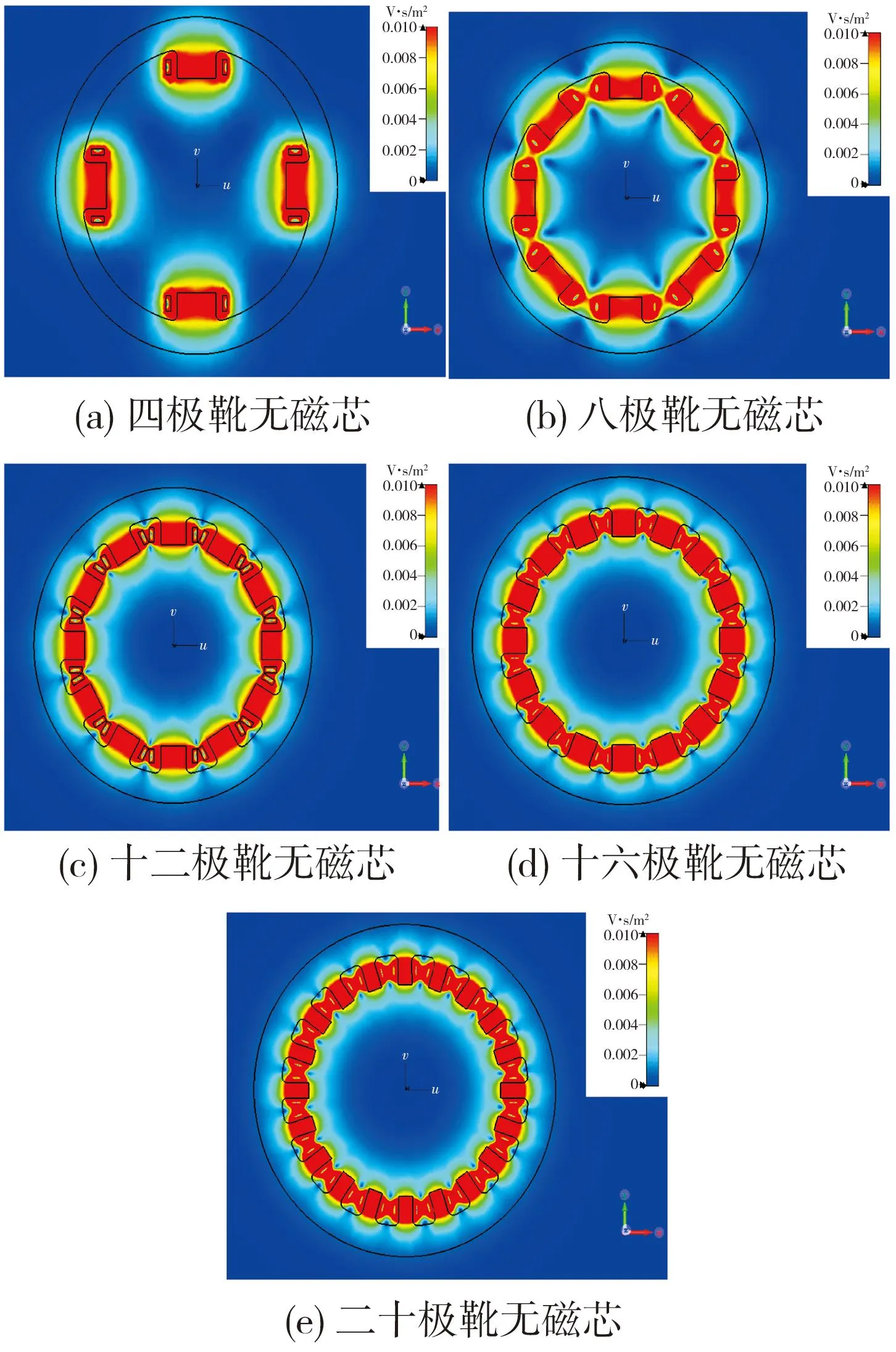
图4 无磁芯线圈磁感应强度分布

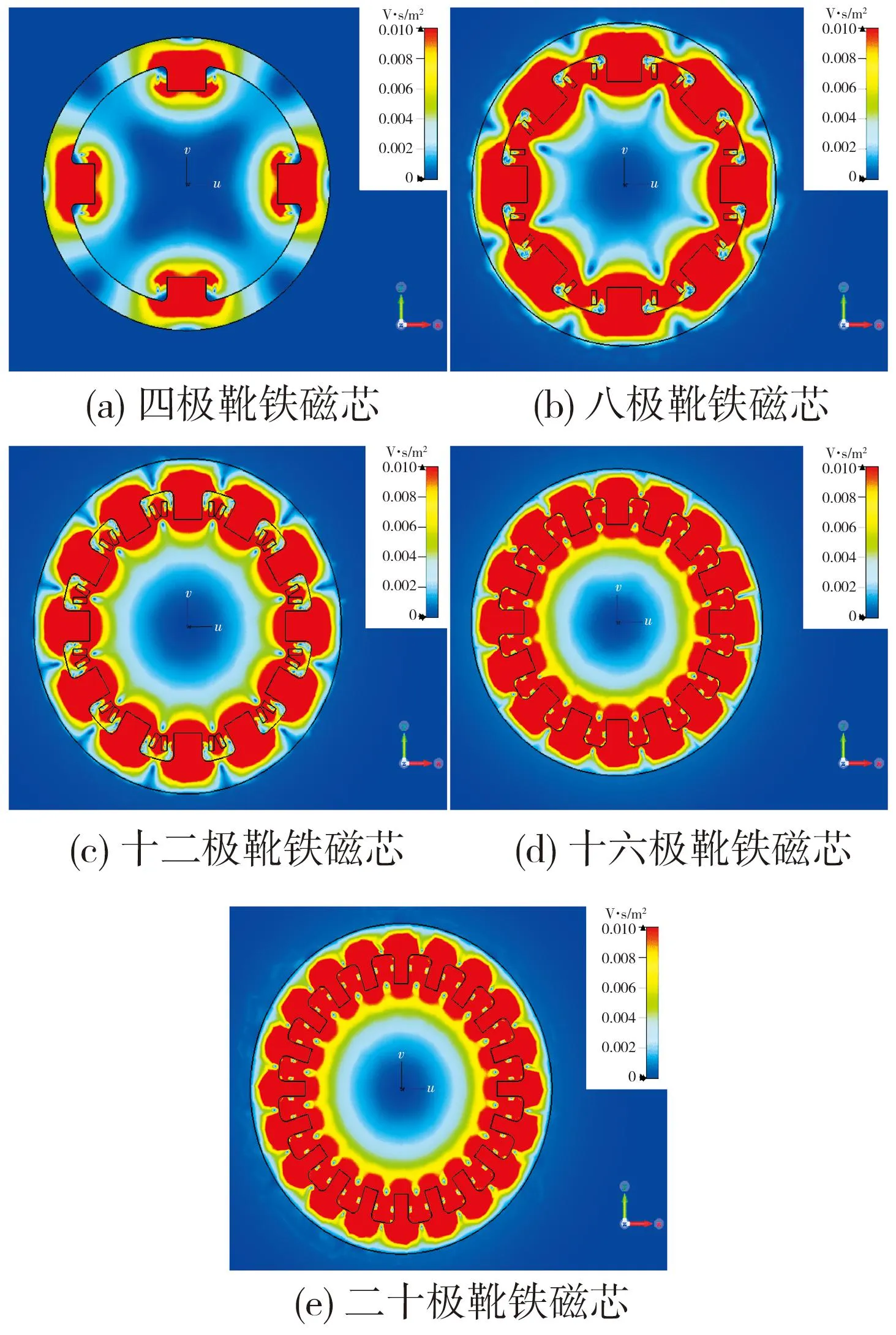
图5 铁磁芯线圈磁感应强度分布

在EBSM成型系统实际工作条件下,电子束偏转角度较小,主要由线圈中心5 mm范围内的磁场状况决定。为进一步研究线圈中心5 mm范围内的磁场均匀性,对线圈中心、距中心2.5 mm位置、距中心5 mm位置的磁感应强度进行分析,结果如表3 所示。

3.2 试验结果极差分析

极差分析法是正交设计中常用的方法之一,其可通过简便的计算和判断求得试验的主次因素、优水平、优搭配及最优组合。计算公式为

(5)

(6)

根据本文试验目的,以最大线圈中心磁感应强度K均值和最小磁感应强度变化率K均值来选取各因素下的最优水平。

3.2.1 线圈中心磁感应强度分析

利用式(5)和式(6)进行计算,得到线圈中心磁感应强度的极差分析结果如表4 所示。

表4 线圈中心磁感应强度的极差分析结果

由表4 可以看出:极靴数和磁芯类型对线圈中心磁感应强度均有一定影响。铁磁芯线圈产生的磁感应强度远远大于无磁芯线圈,极靴数量越多线圈中心的磁感应强度越大。分析可知,铁磁材料里面带有“磁畴”,平时磁畴无规则排列不表现磁性,在通电线圈的作用下,磁畴会规则排列,使铁芯中形成很强的磁通,从而使磁感应强度增大,但铁磁芯线圈存在一定的磁滞损耗,较难实现超高频率信号的实时响应。极靴的主要作用是增大磁通面积,减小主磁场以外的漏磁,所以极靴数量越多,磁通面积越大,漏磁越少,因而磁感应强度增大。

3.2.2 2.5 mm范围内磁场均匀性分析

2.5 mm范围内磁感应强度变化率极差的分析结果如表5 所示。

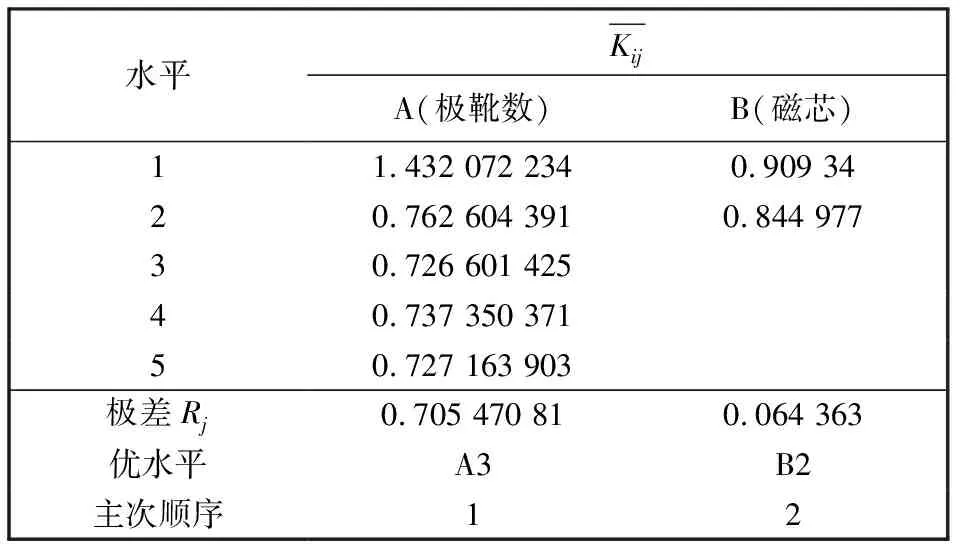
表5 2.5 mm范围内磁感应强度变化率极差分析结果

由表5 可以看出:对2.5 mm范围内磁场均匀度影响最大的因素是极靴数,其次是磁芯类型。八极靴线圈比四极靴线圈的磁场均匀度有极大的提升。十二极靴线圈、十六极靴线圈、二十极靴线圈对比八极靴线圈的磁场均匀度,提升已不明显。铁磁芯线圈相较于无磁芯线圈,磁场的均匀度上没有明显的优势,提升磁场均匀度的效果不如提升极靴数的效果明显。

3.2.3 5 mm范围内磁感应强度均匀性分析

5 mm范围内磁感应强度变化率的极差分析结果如表6 所示。

表6 5 mm范围内磁感应强度变化率极差分析结果

由表6 可以看出:极靴数量对5 mm范围内的磁场均匀度有显著影响,极靴数越多磁场越均匀,但十二极靴线圈、十六极靴线圈、二十极靴线圈对比八极靴线圈的磁场均匀度,提升已不明显。无磁芯线圈相较于铁磁芯线圈在5 mm范围内的磁场均匀度有显著优势,分析可知,铁磁芯的存在使磁感应强度越靠近线圈增加越剧烈,导致磁感应强度变化率增大。

通过以上分析可得,试验因素对于线圈中心磁感应强度、2.5 mm范围内磁场均匀性以及5 mm范围内磁场均匀性均产生不同的影响。综合考虑,以较高线圈中心磁感应强度、较低2.5 mm 范围内磁感应强度变化率以及较低5 mm范围内磁感应强度变化率为优化目标,通过MOEA/D算法对此多目标优化问题进行求解。

4 基于MOEA/D算法的多目标优化

4.1 MOEA/D算法原理

基于分解的多目标进化算法(MOEA/D)将多目标优化问题分解为N个单目标优化的子问题,通过选择、变异同时优化N个单目标子问题,最终获得一组Pareto最优解,其运算流程如图6 所示[14-16]。基于以上特点,MOEA/D算法具有较低的计算复杂度,可以避免陷入局部最优。

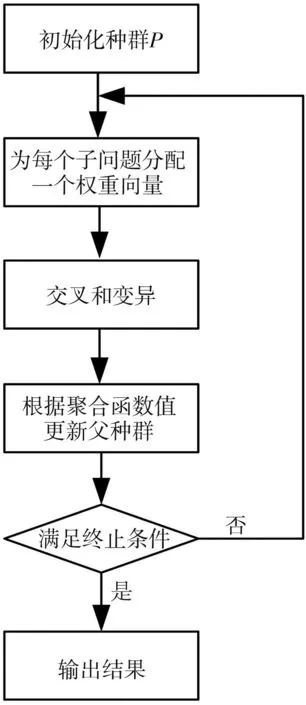
图6 MOEA/D算法流程

4.2 多目标优化方法

MOEA/D算法能够同时优化N个标量子问题,在多个目标问题求解方面具有显著优势,进而可以为工程领域问题提供解决方案。

多目标优化问题定义如式(7)～式(8)所示。

minF(x)=[f1(x),f2(x),…,fm(x)],

x∈Rn,

(7)

s.t.hi(x)≤0,i=1,2,…,p,

(8)

式中:x=[x1,x2,…,xn]∈Rn,为n维决策向量;F(x)为目标函数;fi(x)为适应度函数;hi≤0为不等式约束条件。

4.3 适应度函数构建

试验中优化目标为线圈极靴数以及磁芯类型,首先对试验数据进行处理,把无磁芯条件记为0,铁磁芯条件记为1。基于最小二乘原理,对10组正交试验数据通过多项式拟合法进行拟合,并将方程的最高次项设置为4次,以提高回归方程的置信度。进而得到自变量为极靴数n和磁芯类型c的3个回归方程,并将它们作为MOEA/D算法的适应度函数。

建立线圈中心磁感应强度B的模型,表示为

B=-0.061 15+0.079 73n+0.003 8c-

0.008 606n2+0.121 4nc+0.000 494 1n3-

0.007 051n2c-0.000 010 72n4+

0.000 136 3n3c。

(9)

建立距线圈中心2.5 mm范围内磁感应强度变化率U2.5的模型,表示为

U2.5=4.208-1.048n-0.606c+0.114 5n2+

0.142 6nc-0.005 365n3-0.011 34n2c+

0.000 0911 5n4+0.000 286 5n3c。

(10)

建立距线圈中心5 mm范围内磁感应强度变化率U5的模型,表示为

U5=15.9-3.813n-2.322c+0.409 3n2+

0.497 2nc-0.019 01n3-0.035 49n2c+

0.000 322 3n4+0.000 833 3n3c。

(11)

4.4 目标函数

目标优化的自变量分别为极靴数n以及磁芯类型c,构建模型的矢量表达式如式(12)所示。

x=[n,c]T=[x1,x2]T。

(12)

记线圈中心磁感应强度、距线圈中心2.5 mm范围内的磁感应强度变化率的以及距线圈中心5 mm范围内的磁感应强度变化率的回归方程分别为y1(x)、y2(x)与y3(x),以较大的线圈中心磁感应强度以及较小的距线圈中心2.5 mm范围内的磁感应强度变化率与距线圈中心5 mm范围内的磁感应强度变化率为最优指标,使用优化方法求解最小值,故线圈中心磁场强度求取为min(-y1(x)),距线圈2.5 mm和5 mm范围内的磁感应强度变化率取最小值,即为min(y2(x))和min (y3(x))。因此,所优化的目标函数如式(13) 所示。

minf(x)=[-y1(x),y2(x),y3(x)]T。

(13)

4.5 约束条件

对自变量x1和x2的取值范围添加约束条件,极靴数的约束条件如式(14)所示,磁芯类型的约束条件如式(15)所示。

(14)

(15)

由此可得,自变量x1和x2取值的约束条件如式(16)所示。

h(x)=[h1(x),h2(x)]T。

(16)

综上所述,线圈参数的多目标优化模型为

(17)

4.6 优化模型的求解

根据线圈特性及其使用环境确定线圈结构参数的取值范围,基于MOEA/D算法,并使用MATLAB软件编写M程序进行求解。计算结果如图7 所示。

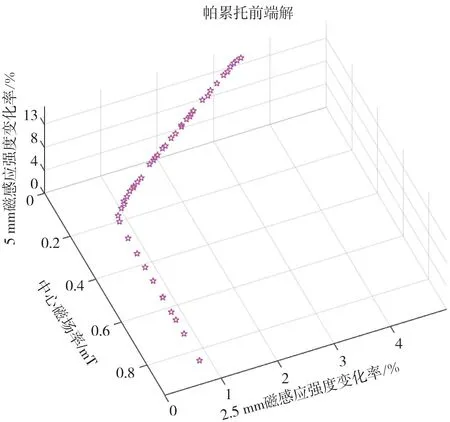
图7 MOEA/D算法计算结果

4.7 优选结果

通过分析结果可得,解集中的最优选择参数产生在极靴数为18、无磁芯的情况下,其磁感应强度分布如图8 所示。表7 中列举了最优参数的仿真结果。分析可知:线圈中心磁感应强度处于较高水平,提高了电子束的偏转角度; 与此同时,距线圈中心2.5 mm和5 mm内磁感应强度的变化率较低,尤其是距线圈中心2.5 mm范围内的磁感应强度变化率均小于1%,可近似看作匀强磁场,这对电子束偏转的精确控制有着积极影响。

表7 3组试验结果对比

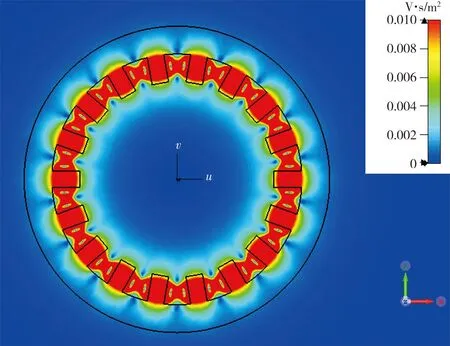
图8 十八极靴无磁芯线圈磁感应强度的分布

5 结 论

本文对多极靴偏转线圈进行了建模,并进行了多极靴线圈静态磁场的正交仿真试验。以增大电子束通过线圈时大角度偏转和精确控制为目标,以极靴数量和磁芯类型为试验变量,并以较大的线圈中心磁感应强度、较小的距线圈中心2.5 mm和5 mm范围内的磁感应强度变化率作为优化指标,通过分析线圈内部磁场云图,得出了磁感应强度分布的趋势。通过对线圈中心磁感应强度和磁感应强度变化率数据的分析,可以得到以下结论:

1) 采用极差分析法对正交仿真试验的10组结果进行分析,可以分别得出线圈中心磁感应强度和磁感应强度变化率在极靴数量和磁芯类型作用下的变化程度,其中,极靴数量和磁芯类型同时对线圈中心的磁感应强度产生显著影响,距线圈中心2.5 mm和5 mm范围内磁感应强度变化率的最显著的影响因素是极靴数量;

2) 利用MOEA/D算法求解线圈设计参数的多目标优化问题,并考虑线圈的实际工艺性以及使用环境,得出十八极靴、无磁芯的线圈结构对于电子束大角度偏转和精确控制有显著优势。