基于粗糙集理论的正交设计提取工艺因素方法的研究

崔红新，杨帅朋，张泞杰，王子翰，黄 琼，赵 迪，冯素香，3

1.河南中医药大学药学院（郑州 450046）

2.河南中医药大学呼吸疾病中医药防治省部共建协同创新中心（郑州 450046）

3.河南中医药大学河南省现代中药研发与应用工程研究中心（郑州 450046）

在药物制剂生产工艺过程中，为了达到最佳工艺条件，技术人员常把因素对工艺的影响作为重要课题研究[1-2]。传统研究因素间关系的常用分析方法包括正交设计、均匀设计及回归分析等，这些方法不仅需要统计的相关性判断、假设检验等，还需要进行大量的试验或足够大的样本量，同时传统统计方法的结果形式比较单一，无法动态分析因素之间、因素和试验结果指标间的相关关系[3-7]。粗糙集理论是一种能有效分析不精确、不完整和不一致信息数据的数学方法，不需要提供所处理数据之外的其他先验知识，而是通过对数据进行分析和推理，挖掘隐含的关系，进而揭示因素之间动态变化的潜在规律。

粗糙集理论目前已广泛应用于数据挖掘、故障检测和工程控制等领域，但在医药领域中的应用较少[8-12]。本研究以《中医药统计学》中“优化经典名方‘四物汤’提取工艺，提高药材的有效成分提取率”为例[13]，以该案例中正交设计试验预处理数据为数据来源，采用粗糙集理论决策方法，探讨四物汤提取生产工艺过程中因素之间的相互作用，提高有效成分提取率，寻求最佳组合搭配。

1 粗糙集理论简介

粗糙集理论由波兰数学家Z.Pawlak 于1982年提出[14]。该理论的基本思路是首先确立考察工艺的因素，对数据资料离散化处理，建立信息表，继而形成条件属性与决策属性的决策表，进行决策表属性约简，利用粗糙集理论的决策分析系统，处理决策表的数据，得出条件属性和决策属性之间的决策规则模型。通过进一步分析决策规则模型，探寻各因素之间以及因素和结果指标之间的动态内在规律。

2 粗糙集模型的建立

2.1 模型因素的确定

本研究旨在探究四物汤提取生产工艺过程中提取时间、加水量和提取次数对试验指标药材多糖成分含量的影响，利用正交设计的正交表L9(34)安排试验，进行预处理[13]，试验因素水平及试验结果分别见表1 和表2。

表1 四物汤提取因素水平Table 1.The extraction factor level of Siwu decoction

表2 四物汤提取因素正交试验结果Table 2.Orthogonal test results of Siwu decoction extraction factors

2.2 决策表及决策规则模型的建立

利用正交设计试验方案的数据作为论域，提取时间、加水量和提取次数作为条件属性，多糖成分含量作为决策属性，条件属性按其数值从小到大进行离散，决策属性按其数值从小到大进行离散，建立因素与试验指标多糖成分含量的相关关系决策表，见表3。

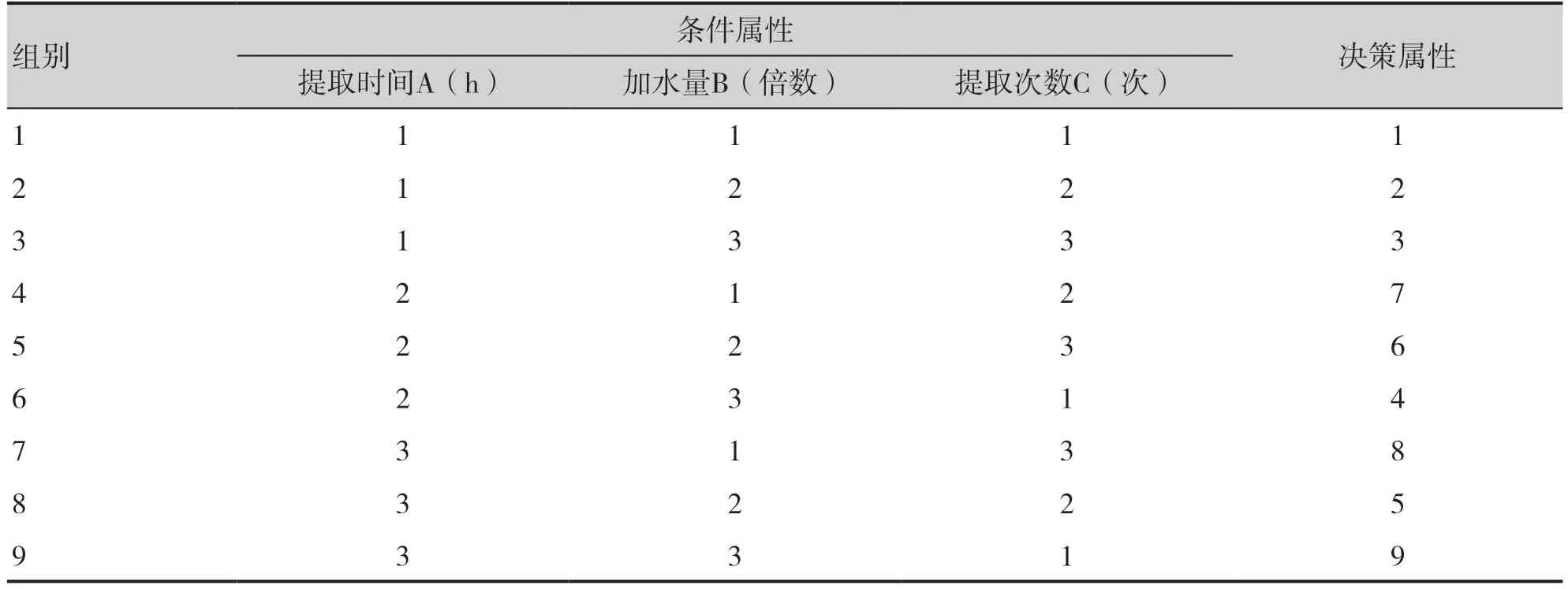
表3 四物汤提取因素水平与多糖成分含量水平相关关系的决策表Table 3.The decision table of the correlation between the extraction factor level and the content level of polysaccharide in Siwu decoction

建立决策表后，进行属性约简，建立决策规则模型：Rx: desc([X]C)→desc([X]D)，其中desc([X]C)表示因素提取时间、加水量和提取次数的特定取值，desc([X]D)表示试验指标药材多糖成分含量的特定取值。决策规则Rx: desc([X]C)→desc([X]D)表示因素提取时间、加水量和提取次数取不同水平时，指标多糖成分含量水平的变化。通过此决策规则模型可以探究因素对多糖成分含量的影响，以及因素之间相互作用的内在规律。

2.3 决策规则模型的分析

采用粗糙集软件Rosetta 进行数据分析，将因素水平与多糖成分含量水平相关关系的决策表载入Rosetta 系统后，软件基于粗糙集理论的KDD决策分析系统，根据粗糙集理论对决策表数据进行处理、逐步分析，得到决策规则结果。按照决策属性的离散原则，决策属性水平越高表示药材多糖成分含量越高，提取效果越好，根据此规则对四物汤提取工艺规则表模型进行分析。利用Excel 软件绘制三维曲面图，横轴分别表示提取时间、加水量或提取次数的水平，纵轴表示多糖成分含量的水平，曲面的不同颜色表示多糖成分含量的不同水平，水平颜色从高到低依次为浅灰色、粉色、浅蓝色、绿色、深蓝、黄色、深灰色、深橘色、橘色。

3 结果

根据Rosetta 软件的决策模型，按照选取支持度均达到最小值0.1 和置信度达到1 的标准，获取Ga（genetic algorithm）规则表，见表4。

表4 四物汤提取工艺模型规则表Table 4.Rule table of the extraction process model of Siwu decoction

由表4 的决策规则1～9 条可以看出，提取时间水平为1、加水量水平为1～3 时，多糖成分含量总水平平均值为6/3；提取时间水平为2、加水量水平为1～3 时，多糖成分含量总水平平均值为17/3；提取时间水平为3、加水量水平为1～3 时，多糖成分含量总水平平均值为22/3。说明当提取时间水平、加水量水平增高时，多糖成分含量水平呈递增趋势，见图1。

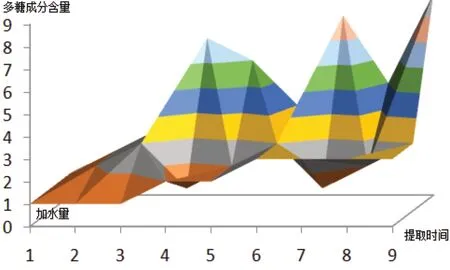
图1 提取时间、加水量与多糖成分含量水平的三维曲面图Figure 1.Three-dimensional curved surface diagram of extraction time, water content and polysaccharide content level

由表4 的决策规则10～18 条可以看出，提取时间水平为1、提取次数水平为1～3 时，多糖成分含量总水平平均值为6/3；提取时间水平为2、提取次数水平为1～3 时，多糖成分含量总水平平均值为17/3；提取时间水平为3、提取次数水平为1～3 时，多糖成分含量总水平平均值为22/3。说明当提取时间水平、提取次数水平增高时，多糖成分含量水平呈递增趋势，见图2。

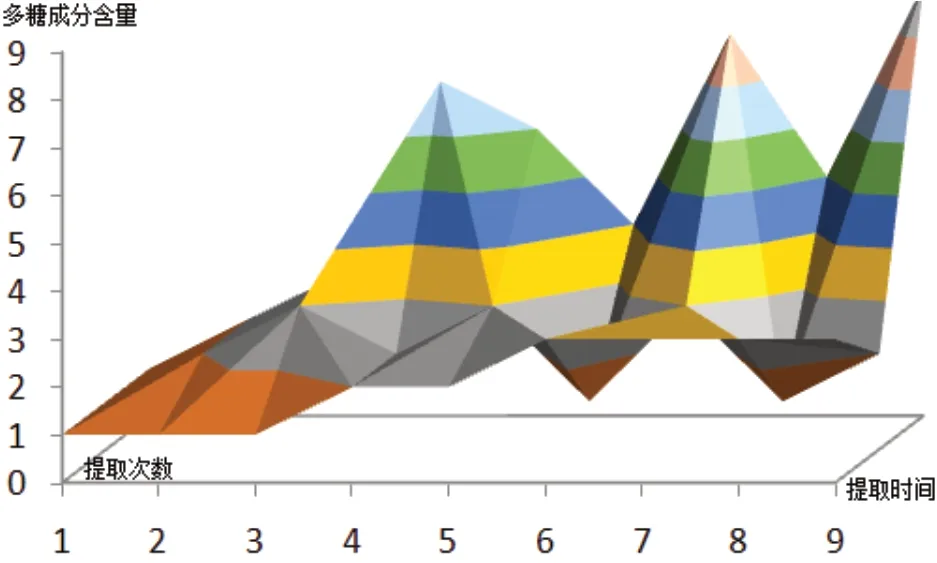
图2 提取时间、提取次数与多糖成分含量水平的三维曲面图Figure 2.Three-dimensional curved surface diagram of extraction time, extraction times and polysaccharide content level

由表4 的决策规则19～27 条可以看出，加水量水平为1、提取次数水平为1～3 时，多糖成分含量总水平平均值为6/3；加水量水平为2、提取次数水平为1～3 时，多糖成分含量总水平平均值为17/3；加水量水平为3、提取次数水平为1～3 时，多糖成分含量总水平平均值为22/3。说明当加水量水平、提取次数水平增高时，多糖成分含量水平呈递增趋势，见图3。

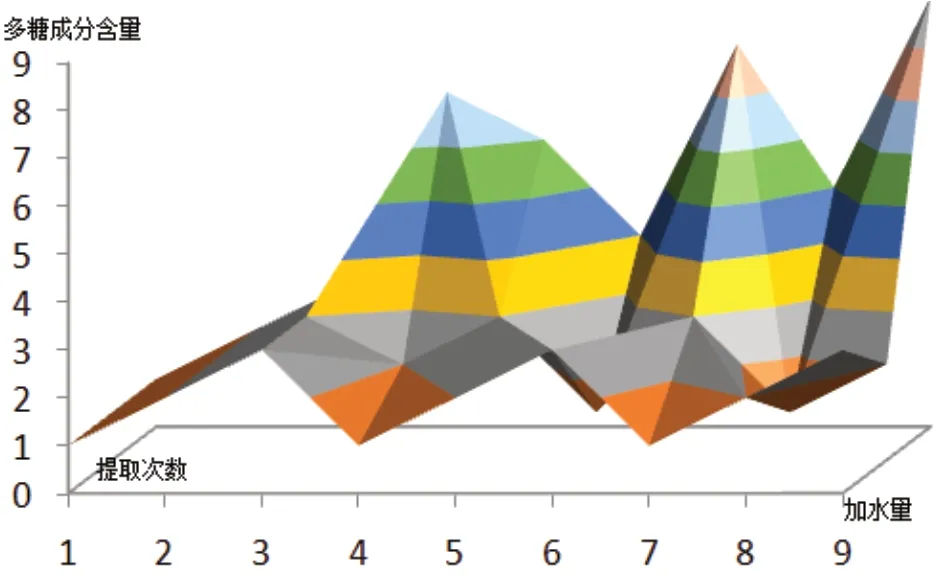
图3 加水量、提取次数与多糖成分含量水平的三维曲面图Figure 3.Three-dimensional curved surface diagram of water addition, extraction times and polysaccharide content level

根据决策规则1～9 可知，当提取时间为3 水平、加水量为3 水平时，多糖成分含量为9 水平；由规则10～18 可知，当提取时间为3 水平、提取次数水平为3 或2 时，多糖成分含量水平为8 或9 水平；由规则19～27 可知，加水量为3 水平、提取次数水平为3 或2 时，多糖成分含量水平为8 或9 水平。综合平衡以上三因素与试验指标的内在关系，四物汤优化提取工艺的三因素三水平最佳搭配为提取时间为3 水平、加水量为3 水平、提取次数为2 水平，即提取时间为1.5 小时、加水量为1 ∶ 20、提取次数为2 次。

4 讨论

基于三维曲面图，结合决策规则中提取时间、加水量、提取次数水平与多糖成分含量水平的动态变化规律可以发现，当提取时间、加水量、提取次数水平均增高时，多糖成分含量水平呈递增趋势。

本研究结果显示，当提取时间为1.5 小时、加水量为1 ∶ 20、提取次数为2 次时，试验结果最好，此结果与参考资料中采用正交设计分析的结果一致[13]。正交设计分析方法是利用方差分析的原理，多次对因素不同水平进行计算，得出最佳搭配，但该方法计算量大，且不能充分反映因素之间的内在联系。本研究采用粗糙集理论方法能够以动态变化形式，以结局指标与三因素不同水平变化影响的过程为研究重点，充分反映各因素之间以及因素和试验结果之间的相关关系，从更深层次揭示因素之间的内在规律。

本研究结果表明，粗糙集理论方法能够有效分析和推理不完整的数据信息，挖掘因素之间的相关关系，它不同于基于概率论为基础的数据挖掘，不需要进行相关性的系列假设检验。与模糊数学理论及证据理论方法的数据挖掘相比，粗糙集理论方法不需要提供所处理信息之外的任何预知知识。因此，该方法可作为医药科学领域解决实际问题的一种实用方法。

综上所述，本研究以四物汤为例，探究工艺因素之间以及因素与结果指标之间的相关关系，应用粗糙集理论决策规则模型的方法更全面地揭示事物之间的内在动态规律，并提供一种新颖的研究方法，从而进一步提高药物制剂的工艺质量。