一种仿人形五指灵巧手的运动学封闭解与仿真研究*
2024-01-03赵树伟王亚鹏
赵树伟,贾 楠,王亚鹏
(长安大学公路养护装备国家工程研究中心,陕西 西安 710065)
0 引言
仿人形灵巧手作为机器人的一种拟人化末端执行机构,具有灵活性高、操作方式多样和适用性强等特点,可以代替人手在医疗康复[1]、航空航天[2]、水下作业[3]、仓物堆放[4]等领域中完成精细的作业任务,成为近年机器人研究领域的热点之一[5]。为了实现稳定抓取与灵活操作,仿人形灵巧手具有关节数目多、运动链复杂的结构设计[6],但也导致其运动学分析困难,运动学模型解算工作量大,增加了后续灵巧手抓取规划和控制系统设计的难度。
为了更好地进行后续研究,例如误差分析[7]、轨迹规划[8]等,就需要建立其运动学模型,即建立灵巧手从驱动空间到手指末端位姿的映射。对于关节串联型手指[9],通过DH法[10]和几何分析的方法[11]可以直接建立灵巧手的运动学封闭解,这种解具有很高的精确性,且计算量小,实时性好。在此基础上通过控制算法,能达到对灵巧手精确的控制。对于手指关节存在耦合的情况[12],通过连杆几何约束关系建立的运动学微分方程具有很强的非线性,难以得出运动学封闭解。对于此类手指机构,目前研究多使用数值仿真或数值迭代的方法进行运动学建模。但这种数值计算的方法计算量大,依赖该方法设计的灵巧手控制系统难以保证较高的实时性。对于关节具有弹性元件的欠驱动灵巧手[13],在指尖满足一定约束条件时,基于系统能量最小的原则[14],可将运动学求解问题转化为一种最优化问题。这种方法不同于传统的基于几何约束条件的运动学建模方法,简化了运动学求解过程,但这种基于能量的方法对灵巧手结构和抓取任务具有严格的限制。随着计算机算力的不断提升,Morgan等人提出了基于数据驱动的方法[15],通过分析大量驱动器数据与末端位置数据形成的“数据对”,建立灵巧手的运动学回归模型。由于这种基于数据的方法摆脱了对真实物理机构的依赖,具有很高的普适性,但难以实现对灵巧手的精确操控。综上所述,为了实现高精度和高实时性的灵巧手控制,有必要对灵巧手的运动学解析模型进行研究。
论文主要研究内容包括以下几个方面:首先,对仿人形灵巧手进行结构分析,对手指关节机构进行分析和简化;其次,采用几何分析的方法求解灵巧手正、逆运动学封闭解;最后,通过与Adams中灵巧手虚拟机的仿真结果对比,验证了求解的灵巧手运动学封闭解的正确性和有效性。
1 仿人形五指灵巧手结构分析
论文研究的仿人形灵巧手具有五根手指,其结构如图1所示,每根手指的外形与尺寸基本仿照人手设计,由近端指段、远端指段和耦合连杆组成,拇指由摆动臂及其附件与手掌相连,其余四指通过指根基座与手掌连接。拇指通过指内直线伺服电机驱动,完成弯曲(伸展)动作,在此基础上,由手掌内直线伺服电机驱动摆动臂实现内收(外展)动作,拇指三个关节按照距基座由近到远分别称为摆动关节、近指关节和远指关节,其结构简图如图2(a)所示。四指各由一个内置在手掌的直线伺服电机驱动,完成弯曲(伸展)动作,每根手指的两个指间关节按照距指根基座由近到远分别称为近指关节和远指关节,其结构简图如图2(b)所示。

图2 手指结构简图
2 仿人形五指灵巧手运动学建模与求解
为更方便地分析灵巧手运动学模型,在灵巧手基座底部圆心建立世界坐标系{W},四指以每根手指的指根基座为原点建立各自的基坐标系(从食指到小指分别为{B1}-{B4})。拇指机构分为弯曲(伸展)机构和摆动机构两部分,由于两部分机构在不同平面内运动,故分别在近端关节处建立弯曲(伸展)机构的基坐标系{B5},在摆动关节处建立摆动机构的基坐标系{B6},如图3所示。由于拇指与其他四指的结构不同,故灵巧手运动学建模分为拇指和四指两个部分。

图3 灵巧手世界坐标系与基坐标系
2.1 仿人形五指灵巧手运动学模型
2.1.1 拇指机构运动学正解
为方便运动学分析,拇指指尖用P表示,机构中转动副分别用字母标记,Li表示简化后各等效连杆,θi表示杆件Li的水平夹角,具体标识如图4所示。记α=∠DCP,β=∠FGH,直线伺服电机驱动连杆L1和L7分别记为Ld1和Ld2,坐标系{B5}原点在{B6}中的表示为B6PB5origin=[B6xoB6yoB6zo]T,坐标系{B6}原点在{W}中的表示为WPB6origin=[WxoWyoWzo]T。参数θ3、θ9、α、β、B6PB5origin、WPB6origin均为通过测量得到的定值。通过几何关系可以得到。

图4 拇指机构运动简图
(1)
(2)
(3)

(4)
坐标系{B5}对世界坐标系{W}的齐次变换,代入B6PB5origin、WPB6origin可以得到,

(5)
其中,
(6)
通过齐次变换矩阵得到拇指指尖P在世界坐标系{W}中的表示,即拇指的正运动学模型为:

(7)
(8)
2.1.2 四指机构运动学正解

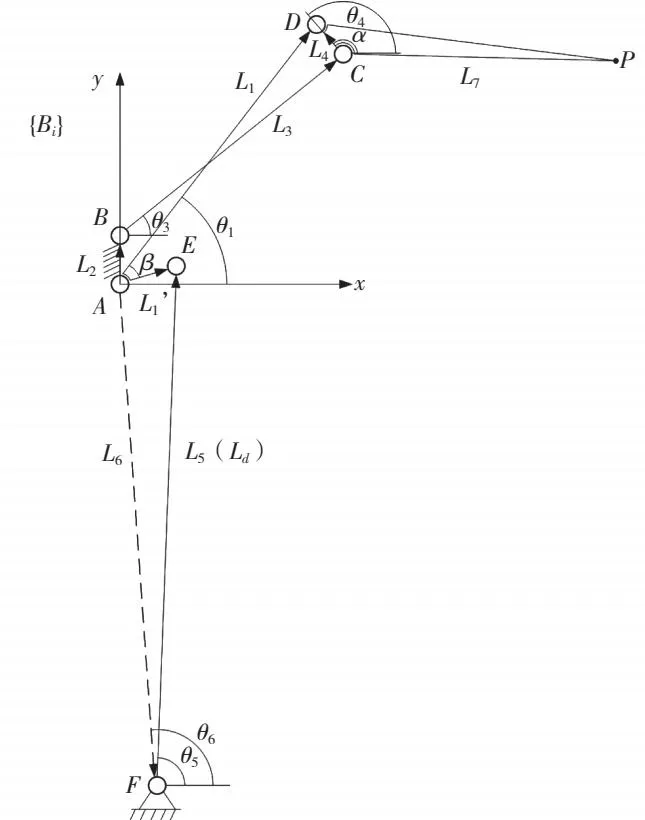
图5 手指机构运动简图
(9)
将式(9)展开解得四杆机构ABCD耦合角度θ1和θ4间解耦关系为:
(10)
其中,
(11)
在ΔAEF中通过余弦定理可以得到,
(12)
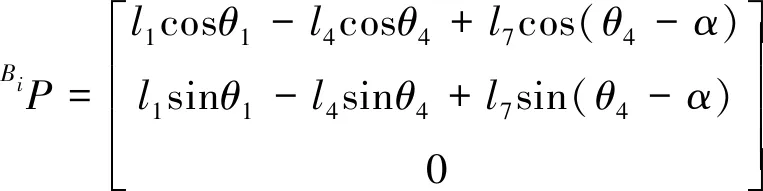
(14)
式中,i=1~4。式(10)-式(14)为四指的正运动学模型。
2.2 仿人形五指灵巧手逆运动学模型
2.2.1 拇指机构运动学逆解
拇指机构的逆运动学具体为,给定指尖在世界坐标系中的坐标WP=[WxWyWz]T,求解直线电机驱动长度,即ld1,ld2。
由式(7)得到指尖在坐标系{B5}的表示为B5P=[B5xB5y0]T,
(15)
取等式的第三行解得,
(16)
其中,a=Wz-Wzo,b=Wx-Wxo,c=B6yo。
取等式第一、二行得到,
B5x=(Wx-Wx0)cos(θ8+β)+
(Wz-Wz0)sin(θ8+β)+B6x0
(17)
B5y=Wy+B6z0-Wyo
(18)
在图4通过几何关系可得,
(19)
(20)
式中,
(21)
(22)
式中,
(23)
(24)
式(19)、式(24)为拇指逆运动学模型。
2.2.2 四指机构运动学逆解
四指机构的逆运动学具体为,给定指尖在世界坐标系中的坐标WP=[WxWyWz]T,求解直线电机驱动长度,即ld。

(25)
在图4基坐标系中通过几何关系可得,
(26)
式中,
(27)
式(25)-式(27)即为四指逆运动学模型。
3 仿人形五指灵巧手正运动学仿真与分析
由于灵巧手的四指结构类似,论文选取灵巧手的中指机构和拇指机构分别进行正运动学仿真,两个手指的仿真参数如表1、表2所示(表中符号的含义与图4、图5中一致)。

表1 中指运动学仿真参数

表2 拇指运动学仿真参数


图6 灵巧手Adams仿真模型


图7 中指指尖位移图8 中指指尖位移误差曲线

图9 中指指尖速度图10 中指指尖速度误差曲线


图11 拇指指尖位移图12 拇指指尖位移误差曲线
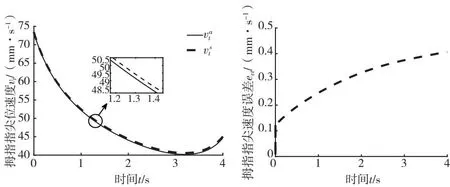
图13 拇指指尖速度图14 拇指速度误差曲线
从图8和图12的仿真结果可以得到中指指尖位移误差|edm|<0.5 mm,拇指指尖位移误差|etm|<0.11 mm。中指指尖和拇指指尖的速度误差如图10和图14所示,其中|evm|<0.4 mm/s,|evt|<0.45 mm/s。从仿真结果可以看出,两种环境下中指和拇指的位移、速度曲线基本一致,证明了所建立的运动学模型的有效性,但由于杆件尺寸的测量误差,其结果存在较小误差。
4 灵巧手工作空间
灵巧手的五指工作空间如图15所示,食指的工作空间与拇指工作空间存在一点交集(即图15中Intersection point),通过联立两根手指的运动学模型解得该相交点坐标为(28.5,192.12,50)T,拇指在x轴方向上的极限位置位于中指和食指之间,表明灵巧手可以完成包括三指抓取在内的抓取操作,具有一定的灵巧性。

图15 五指灵巧手工作空间
5 结论
(1)论文利用几何分析法建立了一种类人形五指灵巧手的正、逆运动学解析模型,为下一步实现灵巧手高精度和高实时性控制系统奠定了基础。
(2)论文利用Adams软件的虚拟样机技术,对灵巧手进行运动学数值仿真,仿真结果表明,运动学解析模型的手指位移误差小于0.5 mm,速度误差小于0.45 mm/s,验证了所求灵巧手运动学解析模型的正确性与有效性,并在此基础上得到了五指灵巧手的工作空间。
