基于模糊RBF-PID的张紧装置电机控制研究

杨威,戴劲松,王茂森

(南京理工大学 机械学院,江苏 南京 210094)

0 引言

在电机控制领域,多电机在协同运行情况下,如何保证多电机运行的同步性以及如何增强系统的抗干扰能力是主要研究内容之一。为了解决以上问题,研究人员提出了多种同步控制策略。潘亮等[1]基于主从控制策略,有效改善了多电机系统的稳定性和动态性能;李言民等[2]采用交叉耦合控制,设计了基于运动控制卡的多轴电机控制系统,并实现了多电机同步位置误差的检测和补偿修正;文献[3]中运用改进速度补偿器的偏差耦合控制,实现了3台伺服电机的比例同步;根据文献[4]中交叉耦合控制结构主要应用于电机之间所产生的实际输出的差值并对两台电机起到补偿作用,可以明显提高电机的同步性且在抗干扰方面具备很大的优势,该控制策略常适用于双电机的控制系统中。在交叉耦合控制中,控制效果在很大程度上取决于耦合控制器的性能。文献[5]使用传统PID控制器作为交叉耦合控制的耦合控制器,仿真实验表明传统PID控制器在对强耦合对象的控制过程中,由于参数无法实时调整,系统的抗干扰能力明显不足,针对该问题,文献[6]采用模糊PID控制器,提高了系统的同步性能,有效改善了当同步偏差较大时易出现超调和反应滞后的现象。

由于模糊规则极大程度上依赖于专家的主观经验,不具备广泛的适用性[7],因此,本文在模糊控制的基础上引入了神经网络控制,设计了一种基于模糊神经网络的PID控制器,并应用于双电机控制系统。

1 某型航炮供弹系统

图1为拨弹轮结构示意图。某航炮在射击过程中,由于自动机高低、方向实时变化,导致供弹传动单元长度变化,并引起该航炮拨弹轮处极易出现拥弹现象,使得弹链停止运动,进而造成航炮的停射。为在不更改弹链本身运动规律的基础上解决该问题,需设计一种张紧装置通过控制拨弹轮部分的运动来调整该处弹链的张紧与放松,从而避免拥弹现象的发生。

图1 拨弹轮结构示意图

本文提出了一种基于双永磁同步电机的张紧装置,弹链张力的控制需要两个电机协同运动,因此,双电机协同控制算法的选择显得尤为重要。目前,两电机驱动的供输弹系统常采用同一给定控制或主从控制,在该控制方案下,两台电机状态互不影响,但在受到扰动冲击时,同步性将大大降低。因此,本文采用交叉耦合控制,并设计了一种基于模糊神经网络的PID控制器,大大提高了两电机的速度同步性和抗冲击性。

2 交叉耦合控制器设计

2.1 交叉耦合控制

传统交叉耦合控制原理如图2所示,这种控制策略是基于观测两种误差:跟踪误差和轮廓误差[8]。在双电机控制系统中,通过检测各电机的速度信息,并将实际转速差作为反馈信号,各电机控制器接收该反馈信号后对电机运行状态进行调节。因此,在交叉耦合控制系统中,任意电机受扰时,另一电机可以根据反馈信号迅速调整自身运行状态,整个系统具有较高的控制精度以及鲁棒性。

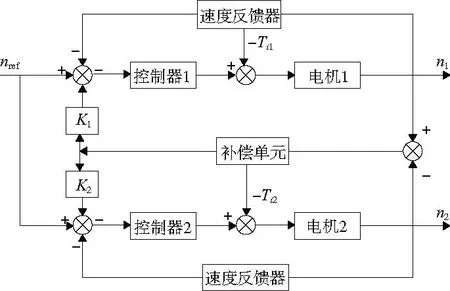
图2 交叉耦合控制原理图

以传统PID控制器作为耦合控制器时,由于传统PID控制器过于依赖其比例系数、积分系数、微分系数的给定,在负载变化的环境中,传统PID控制器无法及时调整自身参数,从而影响控制效果。模糊控制具有推理能力强的特点,将模糊控制与PID控制相结合,可以一定程度上实现PID参数的自整定,但模糊控制规则过于依赖专家的主观经验,虽然直观,但同时也具有一定的不确定性,使其无法在控制过程中对控制规则进行合理的调整,无法明显降低系统的稳态误差。 神经网络控制具有自学习、自适应能力强的特点,弥补了模糊控制没有学习能力的缺点,将两者相结合,可以实现PID控制器参数灵活的在线自整定功能。

2.2 基本模糊PID控制器

模糊PID控制器结构如图3所示,其工作原理为:模糊控制器将转速误差e与误差变化率de/dt作为输入[9],输出为PID控制器的比例系数、积分系数以及微分系数,通过该处理流程实现PID参数的实时自整定。

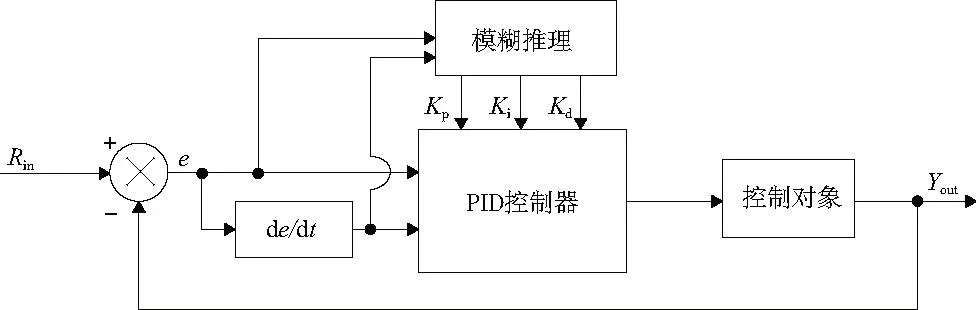
图3 模糊PID控制原理图

2.3 RBF模糊神经网络PID控制器

径向基函数(RBF)神经网络是一种具有单隐层的三层前馈网络,它是一种局部逼近的神经网络,避免了局部极小的问题,非常适合用于实时控制。基于RBF模糊神经网络的PID控制器如图4所示。

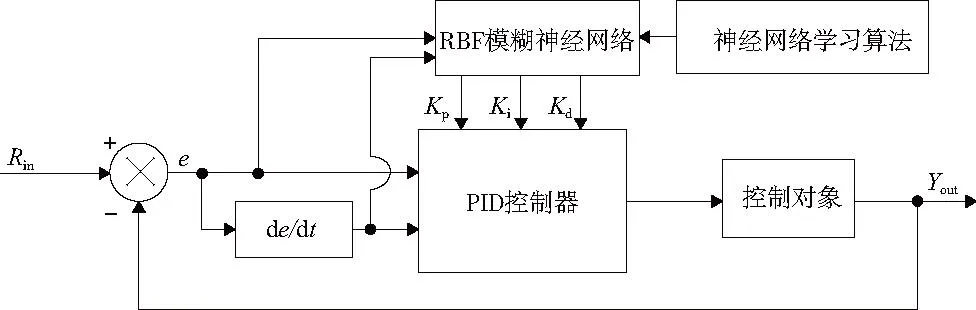
图4 基于模糊RBF神经网络的PID控制器

该控制器在模糊PID控制器的基础上引入了神经网络学习算法,利用神经网络的自学习、自适应特性,在线调整神经网络高斯隶属函数的中心值和宽度、输出层权值等参数。

3 模糊RBF神经网络结构

图5为模糊RBF神经网络拓扑结构,其包括输入层、模糊化层、模糊推理层以及输出层。

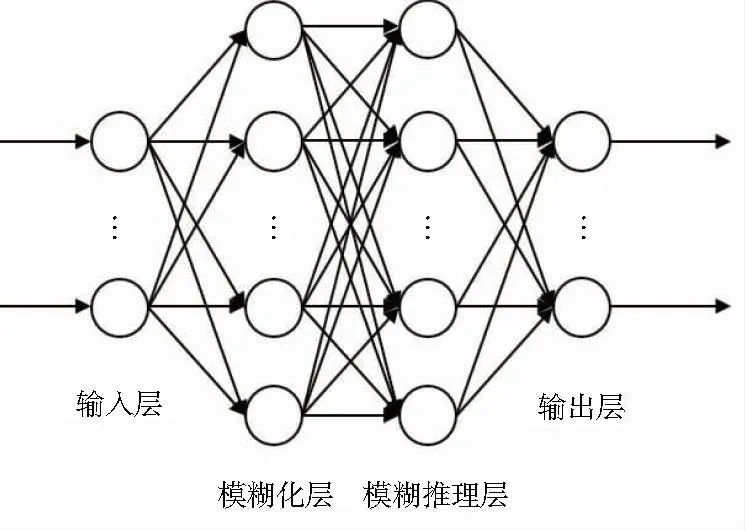
图5 模糊RBF神经网络结构

该神经网络结构中各层输入输出关系如下。

第一层:输入层。该层不进行数据处理,而是将输入数据直接传入下一层,其节点与下一层各个节点相连。输入层的每个节点i的输入输出表示为

f1(i)=I1(x)=Xi(i=1,…,A)

(1)

第二层:模糊化层。该层主要将从输入层传入的数据进行模糊化处理,并对输入分量的隶属函数进行计算,该层节点数量等于输入变量的模糊子集数。选定隶属函数为高斯基函数:

(2)

(3)

式中:cji为第i个输入变量的第j个模糊集合的隶属函数的均值;σij为隶属度函数的宽度值。

第三层:模糊推理层。该层主要进行模糊规则的匹配,该层的每个神经元节点都相当于一条模糊规则,执行and操作,用乘积代替取小运算。

(4)

式中s=s(l,i),s由i和l共同决定,且s∈(1,2,…,B),s(l,i)由下面的规则来决定:

当lmodB=0时,

s(l,1)=B,s(l,2)=[(l-lmodB)/B];

当lmodB≠0时,

第四层:输出层。该层输出经神经网络计算后的结果,即输出Kp、Ki以及Kd的整定结果。

(5)

式中:m为输出层节点的个数;wlm为输出权重。

经过模糊神经网络处理,速度环增量PID控制器:

iq(k)=iq(k-1)+[kp(k-1)+Δkp]·[e(k)-e(k-1)]+[ki(k-1)+Δki]·e(k)+[kd(k-1)+Δkd]·[e(k)-

2e(k-1)+e(k-2)]

(6)

定义系统误差量为

e(k)=V*(k)-V(k)

(7)

取性能指标为

(8)

采用梯度下降法对网络参数进行调节,即按性能指标函数对加权系数的负梯度方向搜索。

(9)

式中:η为学习速率;α为惯性系数;x为需要调整的参数,包括输出权重wlm、隶属度函数中心值cij和宽度值σij。

由式(1)—式(5)可以求得

(10)

(11)

(12)

式中:

(13)

(14)

(15)

(16)

本文以电机实际速度输出和给定速度输出的差值e及其变化率ec作为模糊RBF神经网络的输入,采用模糊推理对Kp、Ki、Kd进行在线整定,以满足不同时刻的e和ec对控制器参数的不同需求。

4 仿真与分析

4.1 仿真模型

根据选定电机参数,基于FOC矢量控制,搭建单电机系统,其模型如图6所示。

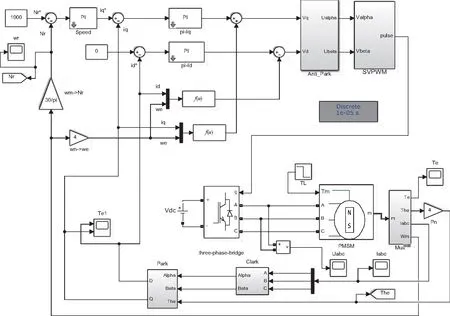
图6 PMSM矢量控制系统

电机参数如表1所示,电机PID参数为Kp=0.2,Ki=10,Kd=0。

表1 电机参数

建立两套相同的伺服驱动单元,并利用交叉耦合控制器将两套驱动单元连接,交叉耦合控制器以两电机的转速差为控制对象,在原有转速反馈上加上控制器的输出。模糊RBF-PID控制器模块利用S函数编写。基于模糊RBF神经网络PID控制器的双电机交叉耦合控制模型如图7所示。

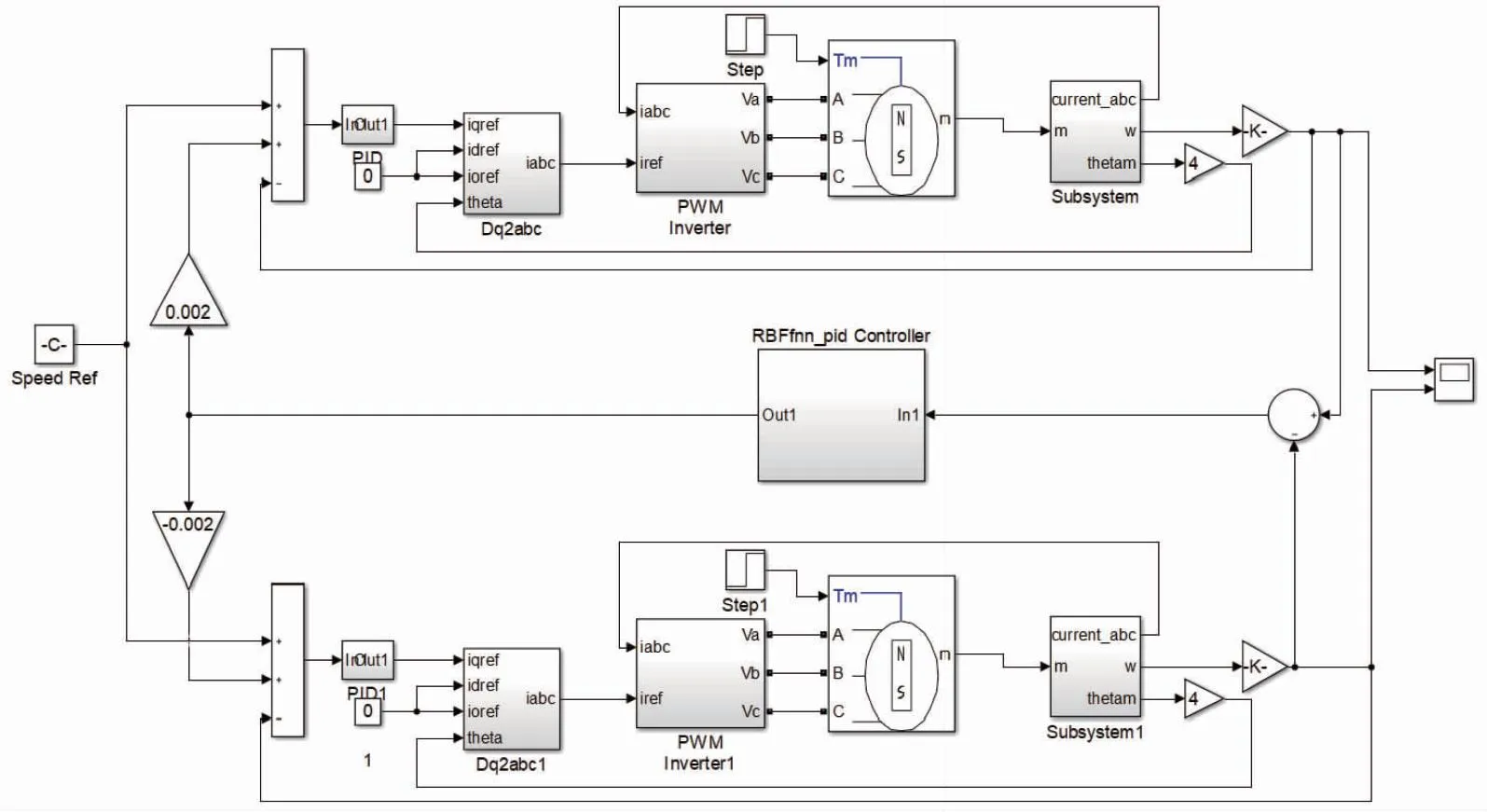
图7 基于模糊RBF-PID的双电机交叉耦合控制仿真模型

分别对以传统PID控制器作为耦合器的交叉耦合双电机系统及以模糊RBF-PID为耦合器的双电机系统进行突加载与突卸载仿真,并对两种控制策略的控制效果进行对比。

4.2 突加负载仿真

给定两电机参考转速为1 200r/min,两电机空载启动。在0.10s时刻,电机2负载转矩从0阶跃到3.5Nm,不同控制策略下,两永磁同步伺服电机的转速w1、w2如图8所示,同步误差如图9所示。

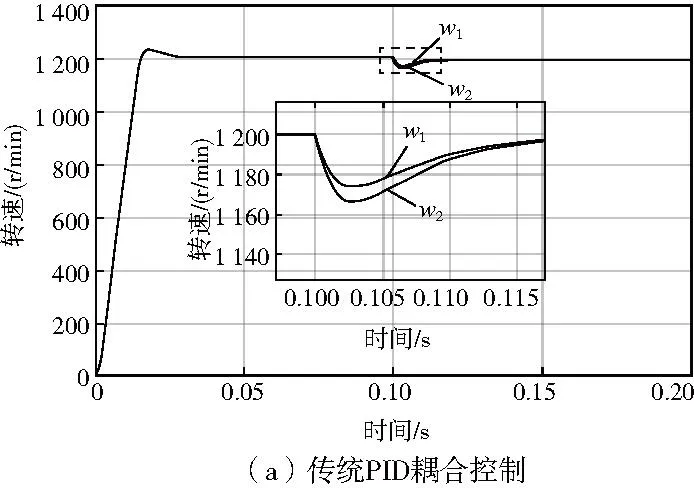
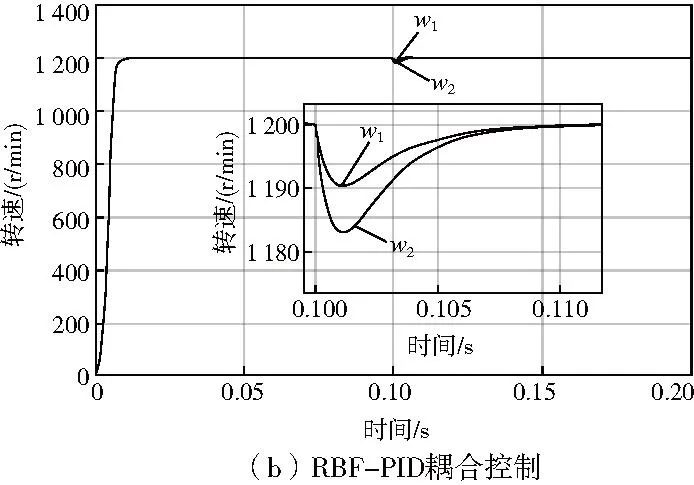
图8 突加负载时两种策略下电机转速曲线

从图8—图9中可以看出,在以传统PID控制器为耦合器的交叉耦合控制中,两电机空载启动时超调量较大,在0.03s左右,两电机达到给定值1 200r/min,进入稳定状态;在0.10s时刻,对电机2突加3.5Nm的负载,此后经过了约0.02s后恢复到参考转速,负载扰动期间,电机转速最大改变量约为34r/min,同步误差峰值为7r/min;而在模糊RBF-PID耦合控制系统中,电机转速最大改变量约为17r/min,同步误差峰值约为7r/min,但在后续过程中迅速变小直至为0,调节时间仅为0.01s,系统同步性能提升明显。

4.3 突降负载仿真

给定两电机参考转速为1 200r/min,两电机带载启动,负载为4Nm。在0.1s时刻,电机1负载转矩突降至0Nm,不同控制策略的两永磁同步伺服电机的转速w1、w2如图10所示,同步误差如图11所示。

图10 突降负载时两种策略下电机转速曲线

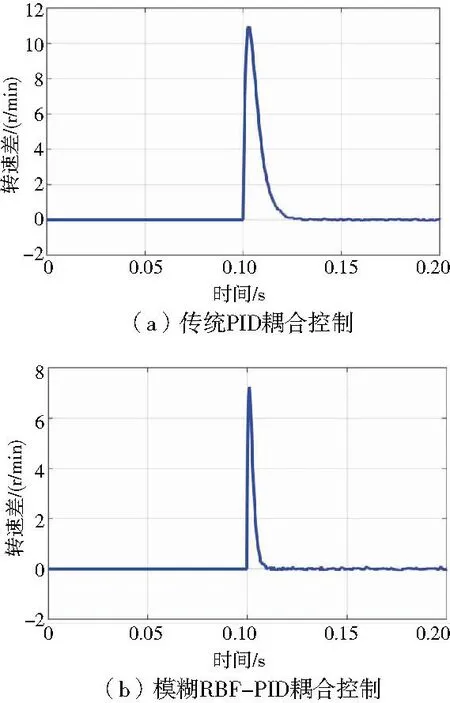
图11 突降负载时两种策略下同步误差曲线

当两电机中一台电机出现突降载扰动时,在以传统PID控制器为耦合器的交叉耦合控制策略下,电机转速最大改变量达到了27r/min,同步误差峰值达到了11r/min;而在模糊RBF-PID耦合控制策略下,电机转速最大改变量约为16r/min,同步误差峰值为7r/min,且调节时间相对于传统交叉耦合明显降低。

5 实验验证

为了验证上述控制算法实际控制效果,本文搭建了双电机同步性能测试系统。系统采用DSP 28335作为主控芯片,采用两台型号为60CST-M01330的电机作为被控对象,该电机额定功率为400 W,额定转矩Ts=1.27Nm,最大转矩Tmax=3.9Nm,电机转子惯量JM=0.29×10-4kg·m2。上位机通过CAN总线与下位机通信并实时采集电机转速数据,双电机同步控制试验平台如图12所示。为了模拟真实环境下电机负载变化情况,实验使用型号为HB-05ML-L的磁滞阻尼器作为电机负载,该阻尼器通过控制输入电流来控制输出转矩,将该阻尼器与电机1连接。该阻尼器主要参数如表2所示。

表2 HB-05ML-L磁滞阻尼器主要参数

图12 双电机同步控制试验平台

本方案所研究航炮的射速为每分钟200发,射击频率约为3.3Hz。随航炮射击时高低俯仰角变化,电机运转阻力变化情况与脉冲状曲线大约一致,因此设计阻尼器电压以3.3Hz方波输入。设置电压方波低电平为12V,高电平为24V,则电机负载转矩最低为0.187Nm,最高为0.487Nm。

给定电机参考转速1 000r/min,运行时间10s,在模糊RBF交叉耦合控制策略下,两电机转速以及转速差曲线如图13—图14所示。实验结果表明,在使用模糊RBF交叉耦合控制策略时,在某一电机外加变化负载情况下,两电机转速差始终保持在8r/min以内,满足实际运行要求。

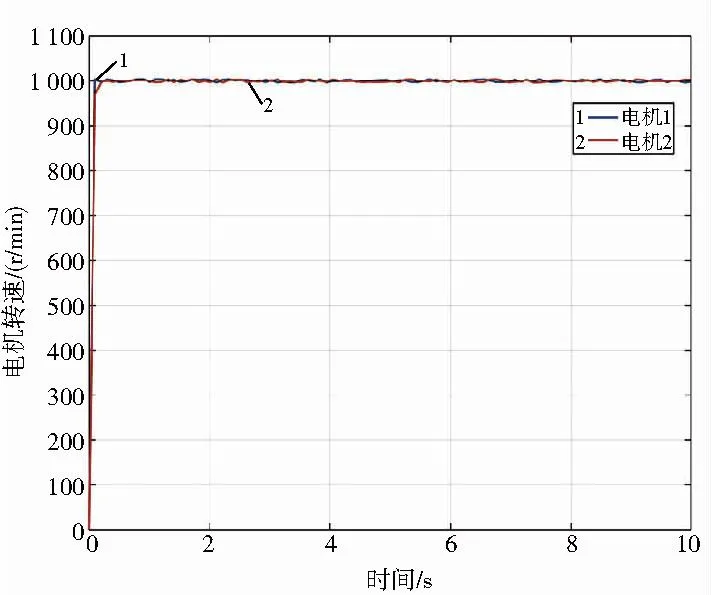
图13 电机转速

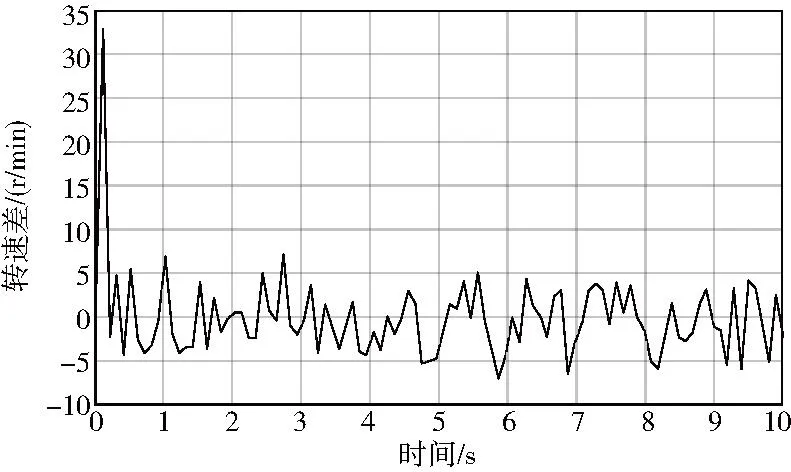
图14 电机转速差

6 结语

在传统交叉耦合控制的基础上,设计了应用于无链供输弹系统中的基于模糊RBF-PID控制器的双永磁同步伺服电机交叉耦合控制方案。相较于以普通PID控制器作为耦合器的交叉耦合控制策略,本方案具有良好的抗扰性能,在负载扰动情况下依旧能保证两电机的同步性能,并且明显缩短了系统恢复时间,满足无链供输弹系统中的双电机速度同步性要求。