协方差分析法在调制型惯导系统设计中的应用

关博帆,胡巍,李四海,杨小康,李炽融

(1.西北工业大学 自动化学院,陕西 西安 710072; 2.中国人民解放军93170部队,陕西 西安 710000)

惯导系统的误差分析是惯导研究的重要内容[1],这里的误差分析主要是指分析不同误差源对最终系统精度的影响。对旋转调制惯导系统来说误差分析这项工作显得尤为重要。在设计旋转策略时,要针对器件的误差特性量体裁衣,有针对性地对影响系统精度程度较大的误差项进行抑制,从而获得较理想的系统精度。在确定旋转策略后,运用合适的误差分析方法计算出各误差源在最终导航误差中的占比,从而评判旋转策略的优劣。快速、准确地获得误差分析结果对于评判、验证旋转调制策略不可或缺。因此,合适的误差分析技术对旋转调制惯导系统具有相当重要的意义。

目前对惯导系统进行误差分析的方法可以分为3种。第一种方法是通过对惯导仿真模型逐次注入特定的误差项进行单次仿真分析,有学者研究了战术导弹惯导系统的误差模型并通过实验验证了不同误差源对系统精度的影响[2],这种方法的缺陷是每次加入的误差是固定值,且忽略了不同误差之间的耦合关系。第二种方法是蒙特卡罗仿真方法,这种方法需要进行大量的仿真[3],对于旋转调制惯导的长航时应用环境来说计算量过大。第三种是协方差分析法,这种方法脱胎于对组合导航系统中卡尔曼滤波器的分析,通过对滤波器中协方差矩阵的分析推导获得各项误差方差和分布情况。研究人员通过推导协方差矩阵的更新方程提出了组合导航系统的误差分析方法[4],还有学者提出了机载惯导进行空中对准时的误差分析方法,并采用蒙特卡罗仿真对误差分析的结果进行了验证[5]。夏家和等[6]运用协方差分析法对传递对准过程进行了分析,获得了各项误差源对航向误差的贡献量。但这些协方差分析方法主要运用在滤波器中,而旋转调制系统是纯惯性系统,导航解算过程中不涉及卡尔曼滤波器运用,需要将协方差分析法引入到旋转调制系统中,设计出适合该系统的误差分析方法。

本文提出了一种相对简单可行的应用于旋转调制惯导的误差分析方法。首先给出了惯导系统的误差模型,并将其改写为线性状态空间模型的形式。然后对状态向量进行了分解,并详细推导了分解后的协方差矩阵更新方程,得到了状态预测误差与初始状态、系统噪声中各误差因素分量之间的关系。根据线性系统的线性叠加原理,揭示了各误差因素之间是相互独立的,状态预测总误差可以分解成各误差因素的贡献量之和,从而简化了误差分析的计算方法。与蒙特卡罗法相比,该方法获得的统计结果在理论上是准确的,并且无需大量的重复计算,计算量更小,耗时更少。最后,对不同的旋转调制策略运用协方差分析法分别进行了误差分析,得到了初始对准误差、IMU常值误差和随机误差等误差源对最终系统导航精度的影响,分析结果能为评估旋转策略的误差抑制效果,提升系统精度提供有益参考。

1 系统的常规误差模型

首先将本文后续分析所用到的坐标系定义如下:i系表示惯性坐标系;e系表示地球坐标系;g系表示当地的地理坐标系,定义为东-北-天;n系表示导航坐标系,本文中选取g系作为导航坐标系。b系表示运载体坐标系,定义为右-前-上。p系表示平台坐标系,即安装IMU的平台所在的坐标系,该平台与IMU固连,IMU随平台转动。当转轴上的测角机构读数为零时,p系与b系重合。

一般情况下的姿态误差可以表示为[7]

(1)

速度误差可以表示为

(2)

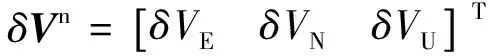
位置误差可以表示为

(3)

式中:L,λ,h分别表示运载体所在位置的纬度、经度和高度;RM和RN分别表示子午圈和卯酉圈的曲率半径。

旋转调制惯导系统的误差模型由3个线性微分方程组成,因此可以将其改写成矩阵乘法形式,如(4)式所示

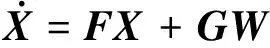
(4)

式中,X是由导航误差和IMU误差组成的向量,可以用(5)式来定义

(5)

(5)式中的向量元素自左到右依次为初始姿态误差、陀螺常值零偏、陀螺标度因数误差、陀螺安装误差、加速度计零偏、加速度计标度因数误差以及加速度计安装误差。需要说明的是,这里的误差项并不是固定的,可根据实际情况增加或减少。

系统误差模型中IMU的随机误差,其向量及分布矩阵由(6)式给出

(6)

向量元素自左到右依次为x,y,z三轴陀螺和加速度计的随机噪声。

(7)

根据系统的误差模型,F可以写成(8)式,而F中一些子矩阵的定义为

这样就得到了旋转调制惯导的线性系统状态空间模型。

2 协方差矩阵更新方程的推导

2.1 根据状态空间模型的推导方法

随机输入线性系统空间状态模型由(9)式给出

(9)

式中:W为随机输入向量。定义X为n×1维的状态向量;W为m×1维的噪声向量。X的离散形式为

Xk=Φk/k-1Xk-1+Γk-1Wk-1

(10)

将(10)式等号两边进行转置有

(11)

将(10)和(11)式相乘可以得到

(12)

(13)

式中:Pk为系统误差的协方差矩阵;Qk为随机误差的方差矩阵。

在第n次更新的时候,经过n次迭代的系统协方差矩阵可以扩写成

(14)

从(14)式可以看出,第n次迭代后协方差矩阵值只与初始的协方差矩阵和随机输入序列有关,如果定义

则(14)式可以写成

以上结果可以用如(19)式所示的协方差矩阵更新公式来概括

(19)

根据协方差矩阵对角线上的每个元素将(19)式分解为

(20)

(21)

则协方差矩阵的更新过程被分解为

(22)

2.2 利用卡尔曼滤波基本方程的推导方法

协方差分析法在惯导系统的应用来源于对卡尔曼滤波器协方差阵的分析,而对旋转调制惯导系来说,应用的是纯惯性算法,并没有外界辅助量测引入系统。但是这里可以借助部分卡尔曼滤波器的思路,摒弃滤波器中的量测更新过程,仅参考其时间更新过程,则可以应用于纯惯性系统的误差分析。

卡尔曼滤波的状态均方差阵Pk一步预测方程为

(23)

在仅考虑时间更新过程的情况下可简写为

(24)

将其不断向前递推可以得到

(25)

一般情况下P0和Q均为对角阵,那么(25)式可以改写为

(26)

(26)式中有

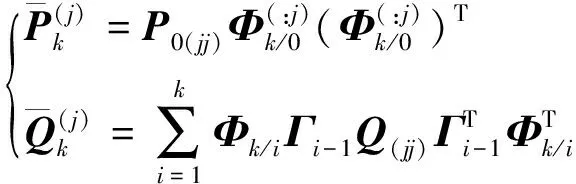
(27)

(28)

如果令

(29)

那么有

(30)

3 调制型捷联惯导的误差抑制原理

通常旋转调制惯导系统的器件误差有陀螺常值零偏ε,加速度计零偏,陀螺的标度因数误差δKg,加速度计的标度因数误差δKa等。

一般情况下陀螺和加速度计的误差模型可以表示为[8]

(31)

(31)式表明陀螺和加速度计的误差模型具有一致性,唯一不同的是陀螺标度因数误差和安装误差与转轴的角运动存在耦合,且考虑到陀螺误差对导航精度的影响更加显著,因此下文以陀螺误差为例分析绕方位轴匀速旋转下的惯性器件误差调制原理。

对于陀螺常值零偏有

(32)

对于陀螺标度因数误差有

(33)

对于陀螺安装偏角有

(34)

可见,在一个旋转周期内δGxy和δGyx无法被调制,而δGxz,δGzx,δGyz,δGzy在一个周期内积分为零,误差得到了抑制。

对于陀螺随机误差有

(35)

旋转前后陀螺随机误差协方差并未发生实质性改变,也即对于陀螺随机误差无法起到周期性旋转调制作用。这是因为旋转调制的频率远小于陀螺随机误差的频率,在一个旋转调制周期内,陀螺随机误差的表现形式仍然是白噪声。

通过对旋转调制误差抑制机理的简要分析可以看出,同一个旋转动作对不同的器件误差项抑制效果不同,类似地,由多个旋转动作构成的整套调制策略对不同的器件误差抑制效果也不同,需要对各个器件误差的抑制效果进行逐项分析,这也正是本文推导协方差分析法的强项。

4 协方差分析法的评估与实际应用

下面使用本文推导的协方差分析法对惯导系统的误差传播过程进行分析,前提是这里的误差必须用方差矩阵的形式来进行描述,以分析陀螺和加速度计噪声的影响。

这种方法与传统的蒙特卡罗方法不同,新方法不需要进行多次的仿真以获取最终误差的统计结果。尤其是旋转惯导主要应用于航海等长航时工作场合,如果进行蒙特卡罗仿真将会消耗大量计算资源和时间,而本文推导的协方差分析法只需进行一次运算即可,是一种简单、快速、可行的惯导误差分析方法。

下面将设计几组典型的场合进行这种分析方法的分析评估和实际运用,分析展示各项误差的传播形式以及对总误差的贡献。

4.1 协方差分析法的准确性评估

最简单的捷联惯导静态导航状态下,各误差项的传播规律相对明确,因而可以与协方差分析法处理过的结果进行对比,验证该方法的准确性。

误差分析用到的相关惯导误差源列于表1中。

表1 误差源设置表

简洁起见,下面仅以经度误差为例展示分析结果。

图1清晰展示了捷联惯导静基座条件下24 h的经度误差以及各个误差项的传播规律和总误差的贡献,从图中可以得到几个结论:

图1 捷联惯导的协方差分析结果

1) 初始水平误差对最终的经度误差影响程度很小,而初始航向误差的影响则不可忽略,这也是提高初始对准精度的意义之一。

2) 陀螺误差对系统总误差的贡献比例要远大于加速度计误差。

3) 静基座条件下陀螺标度因数误差和安装误差对总经度误差的贡献很小,原因是这2项误差需要通过与角运动耦合引入,而静基座条件下的角运动仅有地球自转,其数量级较小,因而引起的误差有限。

4) 陀螺的常值零偏是静基座条件下经度误差的主要误差源。

上述结论与捷联惯导误差分析[9]得到的结论一致,也能从侧面验证该分析方法的合理性。

图2为单轴旋转条件下的经度误差及初始误差贡献,从图中可以看出,初始姿态误差引起的经度误差曲线与捷联条件下完全相同,说明旋转调制技术对初始对准误差无能为力。

图2 单轴旋转惯导经度误差(初始对准误差贡献)

从图3可以看出,水平(x,y轴)陀螺零偏引起的经度误差相对于捷联惯导大幅度减小,趋近于零,说明绕方位轴的旋转调制可以很好地抑制水平陀螺的常值零偏。而z轴陀螺零偏的贡献无变化(图中未标出)。

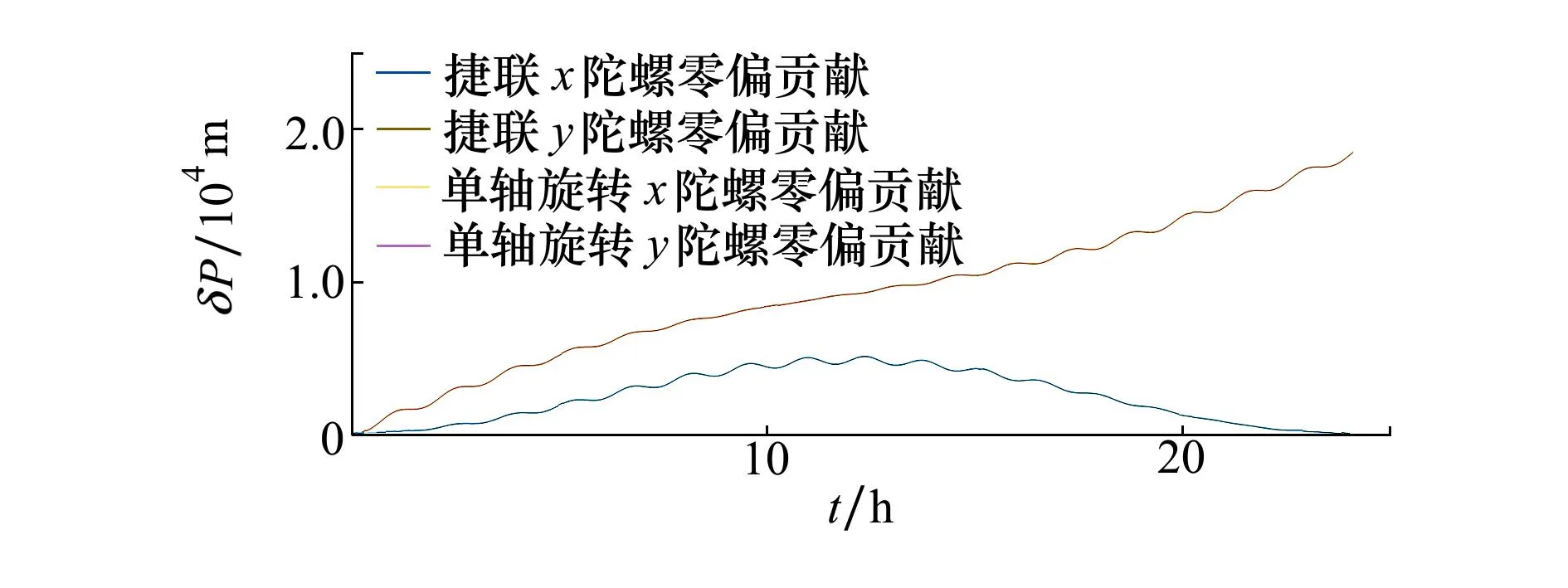
图3 捷联与单轴旋转惯导陀螺零偏对经度误差贡献

对比图1和图2的总经度误差可以看出,系统经度误差最大值从约23 000 m降到了13 000 m,说明单轴旋转调制对提高系统精度有一定效果。

接下来进行单轴旋转与双轴旋转的对比。理论上双轴旋转可以对三轴上的器件误差进行抑制,可以获得较单轴调制更佳的效果,下面用协方差分析法对一种典型的双轴16位置调制方法[10]进行分析。

从图4的经度误差曲线可以看出,三轴陀螺零偏造成的误差相比总误差可以忽略不计(仅为数米),说明双轴旋转可以调制三轴陀螺零偏误差,这也是其与单轴调制的最大区别。

上面几组实例分析的主要目的是将得到的结果与已知结论进行对比,从而验证这种分析方法的合理性以及在旋转调制惯导研究领域的适用性。

4.2 协方差分析法在评价旋转策略的应用

不同的旋转调制策略对不同器件误差项有不同的抑制效果,很难找到一种调制方法能对所有的器件误差项有最优抑制效果,因此要根据系统的器件误差特性等因素来选择最适合的旋转调制策略,这也是设计旋转调制系统非常关键的一个步骤。应用上文推导的协方差分析法可以相对快捷且清晰地获得某种调制策略对各项器件误差的抑制效果,下面通过一个实例来具体分析。将上文提到的16位置方法和一种64位置方法[11]进行对比分析,该64位置方法对陀螺标度因数误差有较好的抑制效果。为了凸显2种调制方法的差别,将陀螺标度因数误差由10×10-6增加为30×10-6,其余条件不变。

从图5可以看出,2种调制方法的差别主要是纬度误差,然后对纬度误差的各个误差源进行绘图。

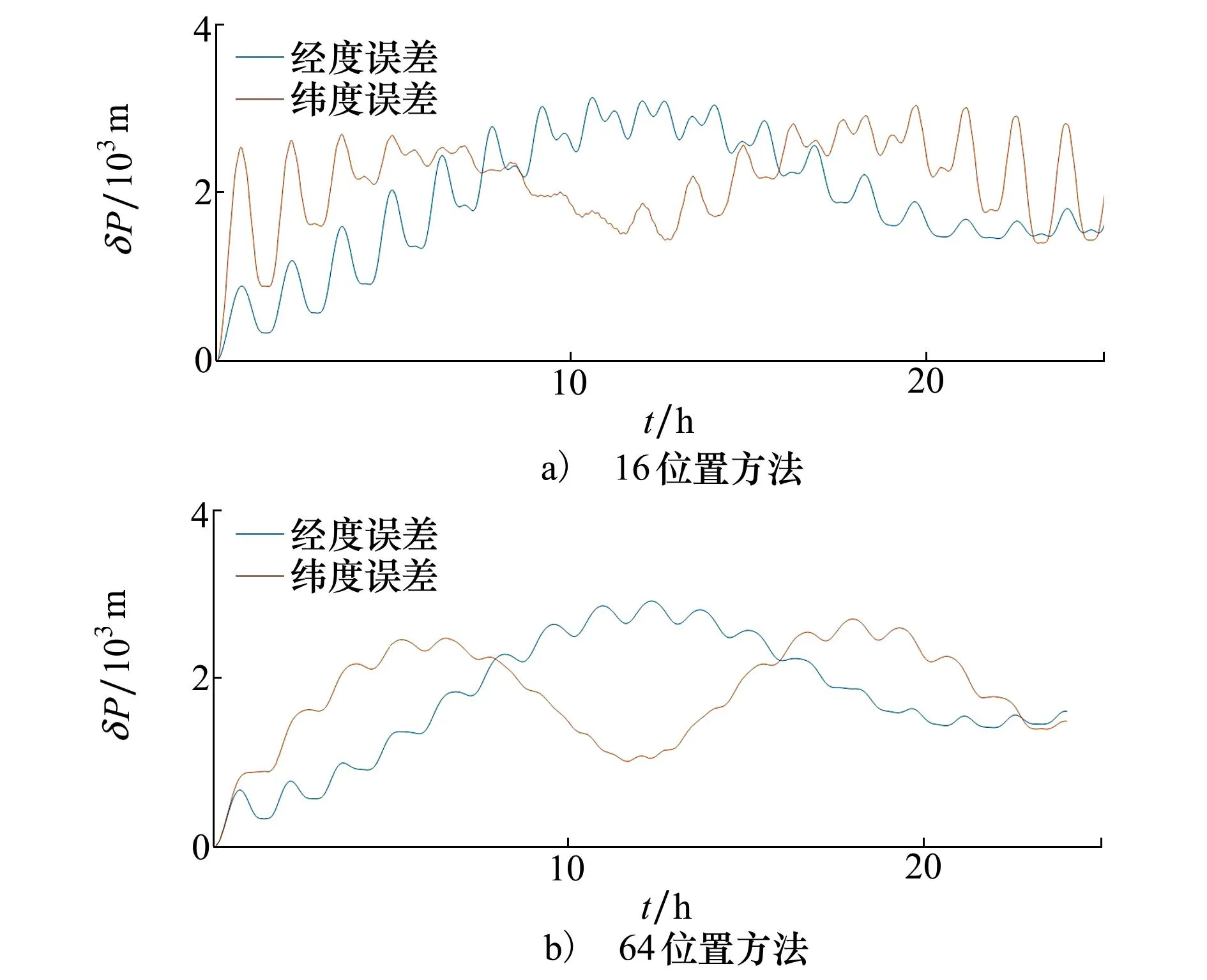
图5 2种调制方法的位置误差图

从图6中可以看出,造成2种调制策略效果差异的主要原因是对陀螺标度因数误差的抑制。如果某系统采用了标度因数性能较差的陀螺,就需要避免采用这种16位置的调制方法。

图6 2种调制方法的纬度误差分解

通过上面的实例分析可以看出,协方差分析法只需运行一次即可获得各个误差项对总误差的贡献,这一特点尤其适合旋转调制惯导的误差分析,可清晰地展示各项误差的传播规律以及与总误差的对比,具有快捷、准确、明了等特点。该方法在惯导系统设计和精度评估中的应用,可以辅助器件选型、系统方案设计、惯导算法优化等环节,协方差分析结果对惯导算法研究和工程应用有一定意义。

5 结 论

本文在根据惯导系统误差模型构建状态空间模型后,将随机误差的状态向量进行递推和分解,推导出了包含初始误差和系统随机误差信息的协方差矩阵的更新方程。利用协方差更新方程即可对系统进行误差分析。这种分析方法仅运行一次即可获得每个误差源的误差分布情况,这就为评判调制策略的优劣以及改进旋转策略提供了依据,并且相较于蒙特卡罗仿真方法更快速简明。因此,这种方法在设计旋转调制惯导系统方面具有较为重要的实用价值,利用协方差分析法得到的结果可以直观看出某种调制策略对某项器件误差的抑制效果,评判调制策略与系统的适合程度,对优化和提升旋转调制惯导系统精度具有较好的指导意义。