基于时序二维化的航空传感器故障检测

2024-01-03张达高君宇丁腾欢谷士鹏李学龙

西北工业大学学报 2023年6期

张达,高君宇,丁腾欢,谷士鹏,李学龙

(1.西北工业大学光电与智能研究院,陕西西安 710072; 2.中国飞行试验研究院,陕西西安 710089)

航空安全在航空运输和军事等领域中具有重要地位,也是临地安防领域研究的关键课题[1]。航空传感器用于实时监测航空器的飞行参数,其详细记录了飞行时温度、压力、迎角等方面的时序信息,对航空器的安全运行至关重要[2]。虽然航空传感器具有较高的设计可靠性,但由于长期运行在空间环境中,其故障无法完全避免。一旦航空传感器发生故障,将严重影响航空器的飞行状态,甚至造成飞行事故。因此,在飞机交付前通过飞行试验校准传感器测量精度进而判断传感器是否发生故障,对于航空器的安全平稳运行具有重要意义[3]。

航空传感器故障是指由于各种因素(包括环境条件、物理损坏和人为错误)导致传感器性能退化,在校准时其输出数据与真实数据出现较大偏差或者错误的现象[4]。传感器的故障检测是指通过对传感器的时序数据进行分析,判断其性能是否在正常范围内工作[5]。航空传感器故障检测的难点在于:①航空传感器时序数据长度极长,通常包含数十万时间点,不易直接进行挖掘;②传统的故障检测方法需要繁琐的人工检验,且难以覆盖到数据的全局信息,缺乏对上下文语义信息的有效建模;③由于不同的试飞任务和条件,每次试飞产生的数据长度不一致,模型训练和测试极为困难。针对航空传感器的故障检测任务,本文通过对传感器数据进行有效挖掘,提出一种基于时序二维化的航空传感器故障检测方法。该方法能及时判断传感器是否发生故障,并降低人工校准传感器的成本,确保航空器飞行过程中数据的有效性。

航空传感器的故障检测主要分为传统方法和基于深度学习的方法。传统方法利用数学手段对传感器数据进行分析,并建立相应的数学模型。例如,于广伟等[6]通过对多尺度迁移符号动力学熵方法的参数进行优选,将其输入支持向量机(support vector machine,SVM)中,从而提升数据驱动故障诊断模型的泛化能力,在少量样本下准确识别不同故障位置。Cui等[7]基于动态时间归整(dynamic time warping,DTW)方法对卫星时间序列中的故障样本进行过采样,结合K近邻(k-nearest neighbor,KNN)分类方法提高对异常样本的检测精度,但处理其他故障数据时效果不佳。Wang等[8]通过带有移项因子的分段聚合近似(piece-wise aggregation approximation,PAA)数据降维方法来降低单元电压时间序列的维度,然后使用聚类算法和异常机制剔除故障样本从而达到检测目的。虽然传统的故障检测方法可以对一些简单的故障进行分析和判断,但对更复杂的故障则需要更先进的技术和方法来进行检测。

相比于传统方法,基于深度学习的方法采用多个隐藏层的神经网络,具备出色的特征提取和学习能力,在样本分类方面显示出独特优势[9]。近年来,此类方法已广泛应用于航空传感器的故障检测研究中[10-13]。例如,王志凯等[14]利用神经网络对燃烧室排放进行监测和控制以确保航空器的安全和稳定运行,为燃烧室排放性能指标的快速评估和精确预测提供了新思路。Zhang等[15]将卷积神经网络(convolutional neural network,CNN)和长短期记忆(long short-term memory,LSTM)深度神经网络结合,提出一种惯性测量单元的检测方法。但此种方法可迁移性差,针对不同异构的数据需要进行不同的网络设计。Dong[16]提出拟图数据堆叠方法,并结合经典的深度学习网络[17-18]来执行故障检测任务。李忠智等[19]将传感器测量数据堆叠为灰度格式的图像,采用VGG16网络判断灰度图的异常区域,然而灰度图只能表示像素点强度,无法表达数据的时间关系,可能会丢失重要的特征信息。Micjail等[20]利用Vision Transformer[9]对卫星图像时间序列进行检测,但缺乏对上下文语义信息的有效建模,模型性能受到较大影响。

基于上述问题,本文提出一种基于时序二维化的航空传感器故障检测方法(time-series to 2D fault detection,T2D),并在民机仿真试飞数据集上进行实验,验证所提出方法的有效性。具体来说:

1) 针对航空传感器超长时序数据,提出一种基于信息熵的分段聚合近似方法(information entropy piece-wise aggregate approximation,IEPAA),充分保留时序特征的同时实现对数据的有效压缩,提高数据挖掘的鲁棒性;

2) 引入格拉姆角场(gramian angular field,GAF),将降维后的一维数据编码为二维图像,从而把故障检测任务转换为图像分类问题,同时又能够保持原始序列的长程时间依赖性;

3) 设计一种灵活的卷积模块(convolutional block,ConvB)并插入检测网络视觉Transformer编码器中,增强对上下文语义信息的编码能力,提高模型的检测精度。

1 T2D架构

本文旨在研究航空传感器的超长时序问题,提出T2D架构,如图1所示。首先,针对极长数据的挑战,提出一种改进的基于分段聚合近似的数据挖掘方法IEPAA(见1.1节);其次,引入格拉姆角场将一维时序数据二维化,把故障检测任务转换为图像分类问题(见1.2节);最后设计一种灵活的卷积映射模块并插入到检测网络中,既增强上下文语义信息建模,又提高模型的检测精度(见1.3节)。

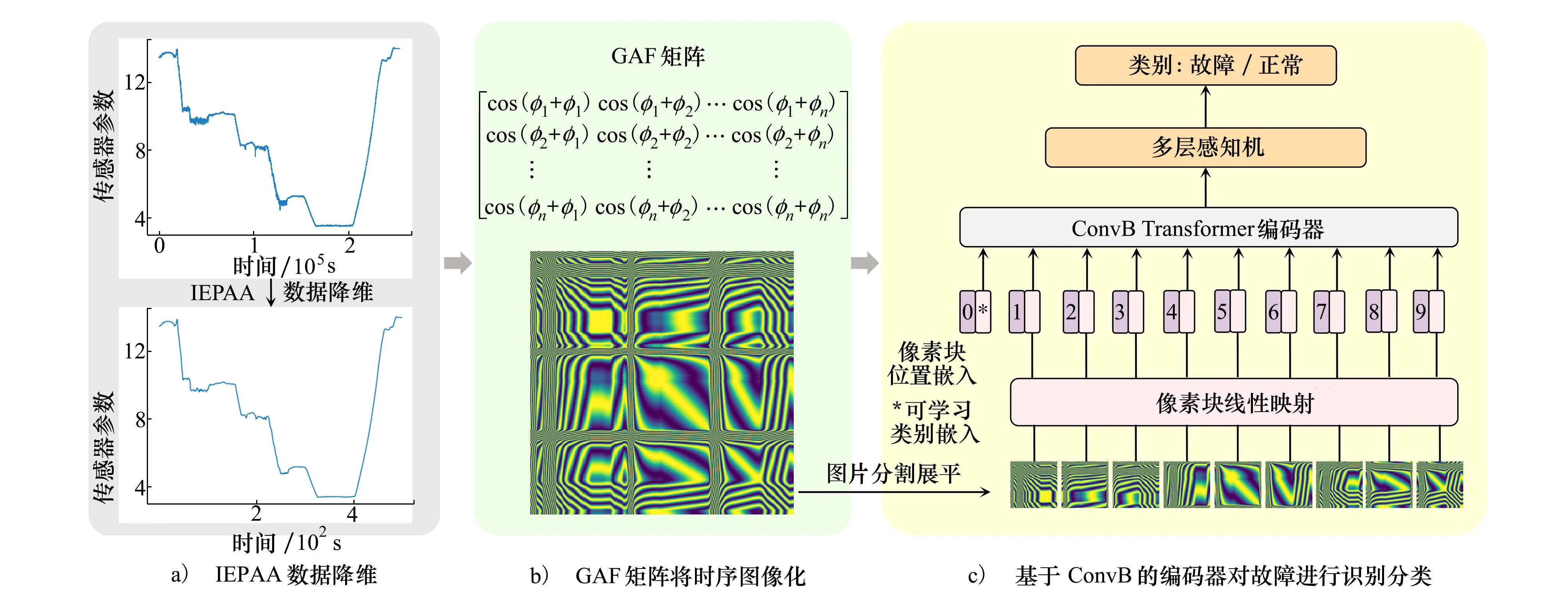
图1 T2D架构图

1.1 基于信息熵的PAA方法

1.1.1 分段聚合近似

Keogh等[21]提出的分段聚合近似(piece-wise aggregation approximation,PAA)是一种时间序列分段表示方法。其思想是对任意时间序列S,利用大小为λ的滑动窗口将其分成多个固定长度的子序列区间,计算各子序列区间内数据的均值,最后将所有计算得到的均值按时间重新排列成新序列S′,用来近似表示原始序列。

(1)

PAA方法将长度为a的时间序列S转变为长度为b的序列S′,实现超长数据压缩过程。虽然降维后的S′能够粗略地表示原始序列的基本形态和变化趋势,但是PAA是均等地对待每个子序列,因此极易忽视局部的数据分布,可能造成较大误差。

1.1.2 信息熵度量

信息熵(information entropy,IE)是指某一事件发生时包含信息量的数学期望,即信源的平均信息量。对于非平稳的航空传感器时序数据,数据曲线的波动程度可以用信息熵来衡量。假设传感器某一时间段的子序列数据为D,其可能有n种取值,分别为d1,d2,…,dn,取值概率为P1,P2,…,Pn,则该时间段的传感器数据D的信息熵值Hn为

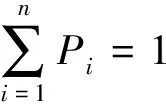
(2)

信息熵值的大小能够反映出传感器数据曲线的波动程度,熵值如果越大,则该段曲线波动的程度越大,代表其复杂程度更高,信息量更多。当每个取值概率都相同时P1=P2=…=Pn时,此组传感器数据的信息熵取得最大值,即Hmax=lnn。

平均信息熵可定义为

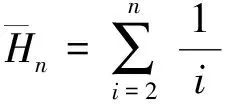
(3)

对于传感器某时间段的数据波动程度,定义νi为第i个波动程度大小,当νi=1时表示数据波动程度大,不能用均值表示曲线波动特征。

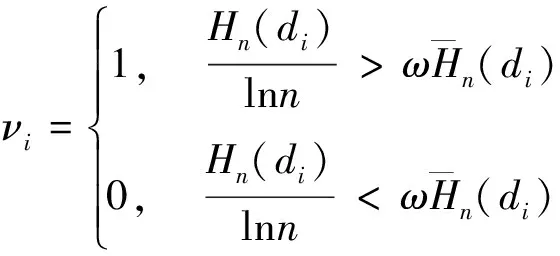
(4)

式中:i=1,2,…,m;m表示该段时间长度;ω是比例系数,一般取1～2。定义α为传感器某时间段数据波动程度大的数量占该段时序数据的比值

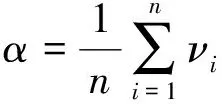
(5)

如果α超过某一个阈值σ,则认为该段时间内曲线波动程度较大,需要更多数据表示曲线特征。

1.1.3 基于信息熵的分段聚合近似方法

基于信息熵的分段聚合近似方法(information entropy piece-wise aggregate approximation,IEPAA)是对PAA算法的改进。IEPAA首先对时间序列进行划分子序列处理,利用信息熵度量求出各子序列区间信息熵。信息熵值越大,表明该子序列区间复杂性越高,越不平稳。按照熵值大小比重分配各区间段数,熵值越大、越复杂的子序列分配数越多,在用PAA求取原序列的近似时,对此区间的近似表示越精确。IEPAA的算法描述如下:

输入:原始序列S={t1,t2,…,ta}。

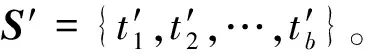
1) 将序列S分成φ个子区间:

φk=[t(k-1)a/b,tka/b], 1≤k≤φ

2) 对每个子区间求信息熵:

3) 确定φk子序列的分段数Fk:

4) 用PAA方法将区间φk表示成长度为Fk的序列;

相比于普通的PAA方法,IEPAA方法可以发现时间序列中极端且短促的变化,对于突变信息能更好地捕捉,拟合原序列时更加逼近。

1.2 基于GAF的时序二维化

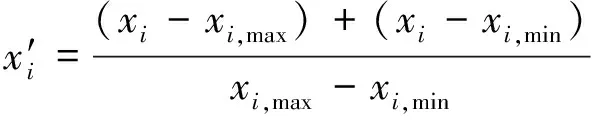
(6)

将所有值都缩放到[-1,1]中,之后利用极坐标序列保留序列的绝对时间关系,从而维持原始序列的长程时间依赖性。将归一化得到的数据进行极坐标系变换,得到每一个数据点对应的半径和角度

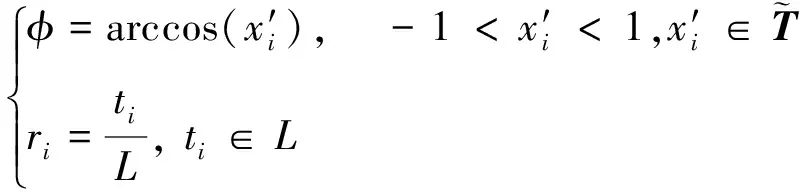
(7)

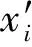
x⨁y=cos(θ1+θ2)

(8)

式中,θ1,θ2分别表示向量x,y在极坐标系中对应的角度,得到时间序列的格拉姆角场如下

(9)

在GAF矩阵中,对角线由归一化处理后的原始值构成,且时间随对角线依次增加,因此时间维度也被编码到GAF矩阵中。由时序数据转换成GAF的完整过程示意图如图2所示。

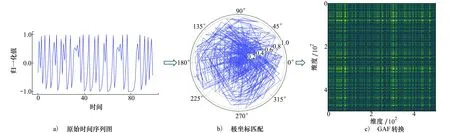
图2 时间序列GAF转换过程示意图

1.3 基于ConvB的视觉Transformer

1.3.1 视觉Transformer

视觉Transformer(vision transformer,ViT)[9]是第一个完全依赖Transformer结构的计算机视觉模型。在ViT中,首先将图像分割为离散且非重叠的像素块,之后添加位置编码并输入到Transformer层中进行分类。虽然ViT在大规模数据集上效果很好,但是对于航空传感器此类少量数据进行训练时,其效果仍低于卷积神经网络(convolutional neural network,CNN)[23]。笔者认为其原因是ViT可能缺乏CNN结构固有的某些更适用于视觉任务的特性。同时,CNN的模式能够考虑到不同复杂程度的上下文信息,从简单的边缘和纹理到高阶语义模式。

针对上述问题,将卷积引入ViT结构中,如图3所示,在保证较高效率的同时增强上下文语义信息的编码能力,提高模型的检测精度。

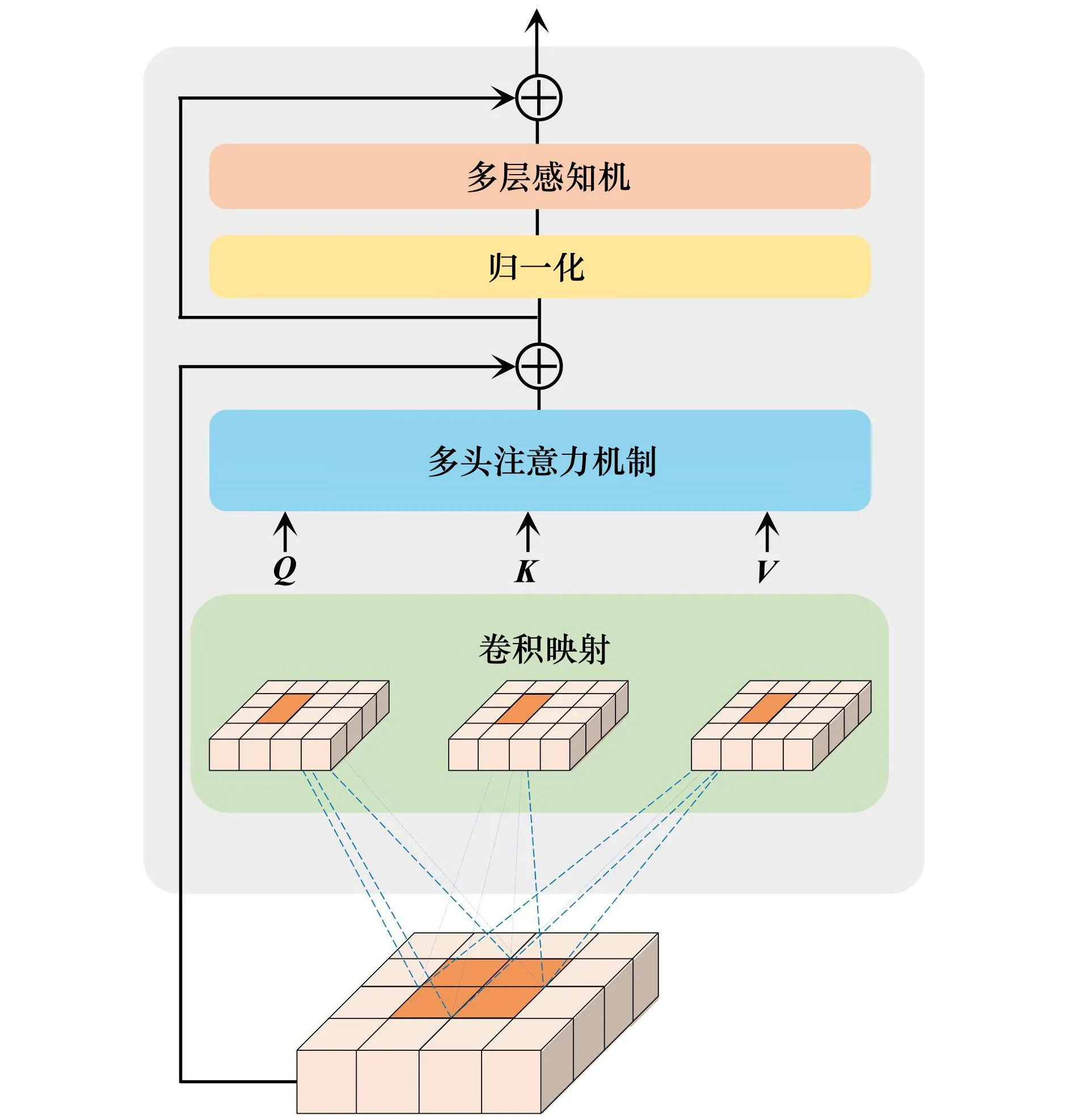
图3 ConvB ViT结构图

1.3.2 ConvB ViT

1) 像素块嵌入向量表示

给定具有高度H、宽度为W和通道C的图像M∈RH×W×C,其被重塑为由N(N=HW/P2)个大小为P×P×C的像素块MP组成的序列。之后通过可学习的线性投影将每个像素块展平成D维的潜在向量,此过程称为像素块嵌入向量表示。最后可学习的位置嵌入Epos添加到嵌入向量序列一并送入ConvB ViT编码器模块中。嵌入公式为

(10)

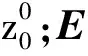
2) ConvB ViT编码器

ConvB ViT编码器包括卷积映射层、多头自注意力层(multi-head self-attention,MSA)、归一化层和多层感知机(multi-layer perceptron,MLP)模块。本文所提出的卷积映射层目标是实现局部空间上下文的额外建模,并通过允许K和V矩阵的欠采样来提高效率。如图4所示,首先将每一个嵌入向量重塑为二维的矩阵映射。之后使用核大小为s的深度可分离卷积层实现卷积映射。最后,将映射矩阵展平为一维向量,用于后续处理。公式为

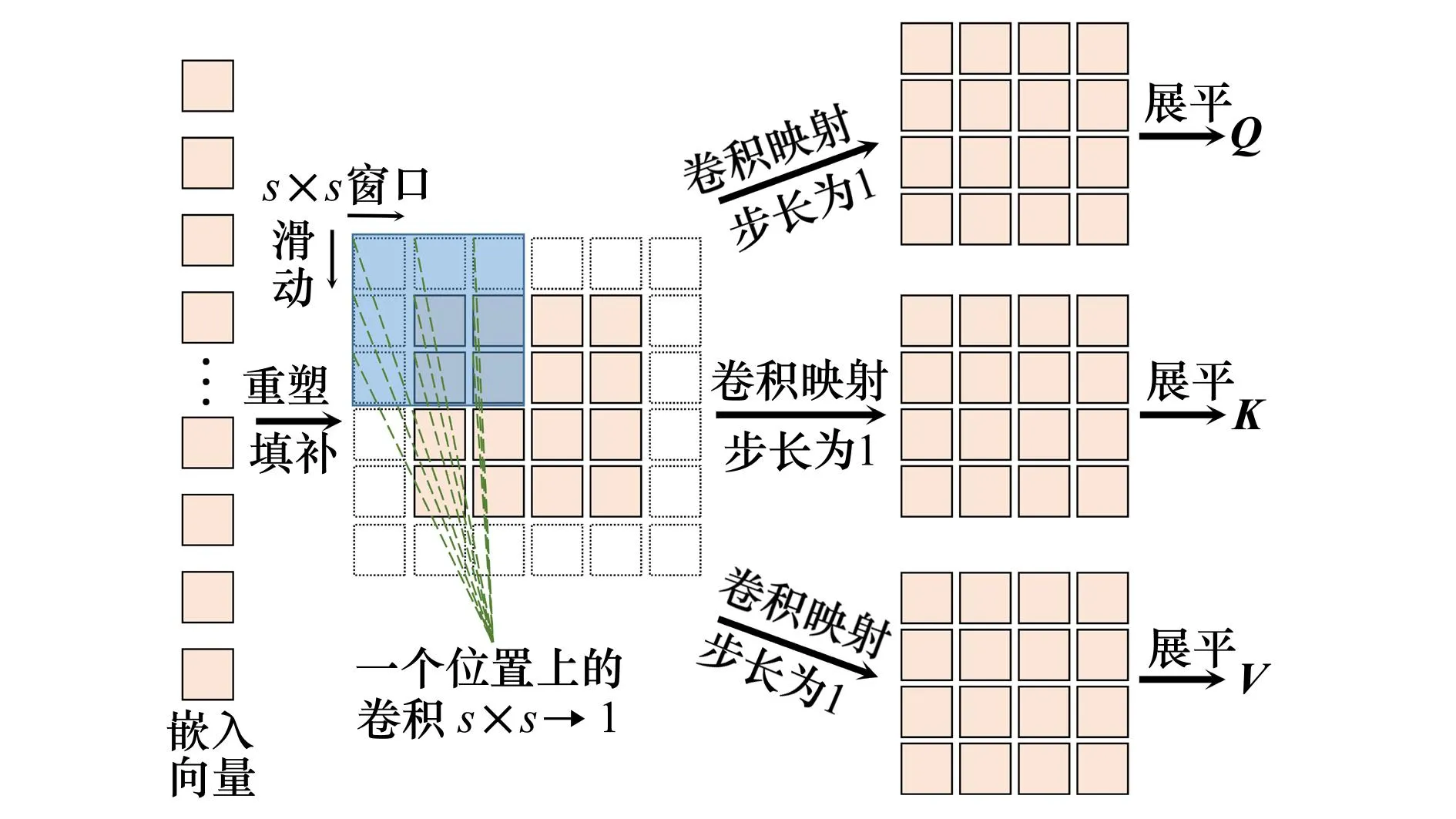
图4 卷积映射示意图

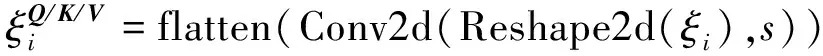
(11)

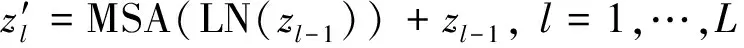
(12)

多层感知机公式为

(13)

式中,LN表示稳定训练的层规范化[24]。

2 实验与分析

2.1 数据集及评价指标

本文采用的数据集来自某民机试飞的仿真数据,包含传感器正常工作及发生故障2种类别,共计700个样本。其中,训练集包含310个正常样本和40个故障样本,测试集包含310个正常样本和40个故障样本,样本平均长度为254 067的时间序列。图5展示出传感器的2种状态记录,通过将原始数据降维并转换成图像的方式呈现,清晰地观察到传感器在正常工作和发生故障时的特征高度相似,为了更为直观地表示2种状态差异,绘制出图6所示的差异图,可以看出相比正常传感器,故障传感器工作时总有偏差。

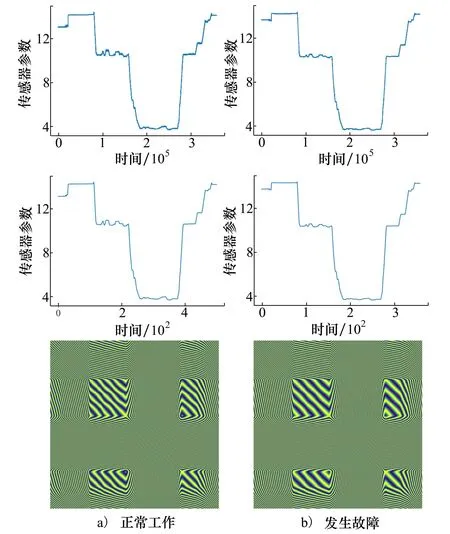
图5 传感器状态记录图

图6 传感器状态差异图

本文采用混淆矩阵(confusion matrix,CM)模型性能评价方法,如表1所示。

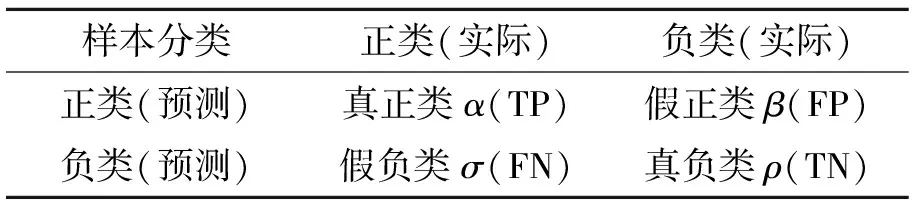
表1 混淆矩阵

该方法在二分类问题中将样本分为正类和负类,例如真正类α(true positive,TP)指实际为正类且被模型预测为正类的样本,假负类σ(false negative,FN)指实际为负类但被模型预测为正类的样本。对分类问题而言,评估分类器最直接的是分类精度γ(accuracy),即分类正确的样本数占总样本的比例。其他评价标准指标有准度κ(precision),表示在所有预测为正的样本中实际为正样本的数量;召回率ω(recall)表示在总体正样本中预测为正样本的数量;F1值μ表示精度和召回率的调和平均。

2.2 实验设置及实验环境

本文旨在验证T2D模型的性能,为此在同一平台下进行多组对比实验,将所提算法与部分经典算法和当前主流模型进行评估,并使用准度故障检测数据集作为评价基准,考察模型在精度、召回率和F1值等评价指标上的表现。对比算法包括支持向量机(SVM)[25]、多层感知机(MLP)[26]、循环神经网络(RNN)[27]、BBN[28]以及GTDA[3]。对比算法是故障检测领域中广泛使用的模型,能够全面客观地评估T2D模型的性能。

本文采用ViT-B[9]作为T2D的骨干网络,并使用Pytorch工具包[29]在24G显存的NVIDIA GeForce RTX 3090上训练T2D模型。首先将数据压缩维度设置到500将原序列降维,通过GAF将训练集图像短边设置成256,按比例调整图像大小,之后对图像随机水平翻转并裁剪成224×224的大小。实验训练批数量为32,所有训练都使用带有0.9动量的Adam优化器实现,初始学习率设置为10-3,总训练的轮次设置为100。

2.3 实验结果

2.3.1 对比实验

展示本文提出的T2D架构数据降维及二维化模块对于试飞仿真数据的格式转换相关参数见表2。

表2 数据对比

表2展示出原始数据和图像化后的数据对比信息。从中可以看出,T2D将超长试飞时序数据分段聚合近似之后再二维化,显著降低了数据规模。具体来说,对于平均长度为254 076且平均占用内存大小为2 032 735 bit的样本,其转换为500×500分辨率图像的平均占用内存大小为8 897 bit,数据压缩为原来的0.43%。

表3通过分析不同算法在试飞仿真数据集中的实验结果来评估本文所提出T2D框架的性能,加粗字体表明结果最佳。从表中看出,T2D框架的准度为91.33%,低于GTDA的92.67%和BBN的91.70%。但是T2D算法的精度、召回率以及F1值分别为88.28%,92.44%,91.88%,在F1值上略高于GTDA的91.75%,在精度和召回率上远高于GTDA的85.71%和90.84%,并且在精度、召回率以及F1值方面显著高于BBN。在所有的指标上,T2D结果都显著高于其他经典的故障检测方法。

表3 不同模型对比结果

另外,通过实验可以看出,T2D框架和GTDA方法的实验结果都明显高于SVM、MLP、RNN这些方法,类似后者的这些模型,对于数据集中超长时序数据的全局语义信息提取能力较弱,并且类似的网络对于一些局部上下文信息编码的水平较差,这可能是导致其性能差的原因。对于T2D的表现,可以归功于两点。首先是在数据降维时以信息熵值的大小作为某一区间复杂程度的评价指标,能够更高地保留这一区间的信息。通过IEPAA方法能够发现序列中短促而异常的变化,对于非平稳的突变信息能够更好地捕捉,对于原时序数据拟合地更加逼近。此外,在进行特征提取时,本文提出的ConvB卷积映射模块能够通过局部感受野引入局部上下文,在ViT使用位置嵌入的同时,能够更好地适应不同输入分辨率大小,在保持模型高性能的同时又具有良好的泛化性。

2.3.2 消融实验

为了进一步分析所提出的T2D框架,本文对超参数以及设计的模块进行了一些消融实验。

1) 各个模块作用

为了进一步了解所提出T2D方法中每个组件在整个模型的作用,在试飞仿真数据集上进行逐步验证,配置如下:

(1) PAA+ViT:未改进的分类聚合算法进行数据降维,并使用最基础的ViT进行故障分类;

(2) IEPAA+ViT:使用基于信息熵的分类聚合算法压缩数据,并结合ViT对二维化后的数据分类,压缩后的数据维度设置为500。

(3) PAA+ConvB ViT:使用未改进的分类聚合算法将数据同样压缩至500维,使用带有卷积映射的ViT,其中卷积核大小设置为3,即s×s=3×3。

(4) IEPAA+ConvB ViT:使用基于信息熵的分类聚合算法将数据压缩至500维,同时使用带有卷积核大小为3的卷积映射通过ViT进行分类。

表4列出了每个模型通过不同模块的配置在试飞仿真数据集上的结果。除了基础模块及改进模块不同外,其他基本设置全部相同。

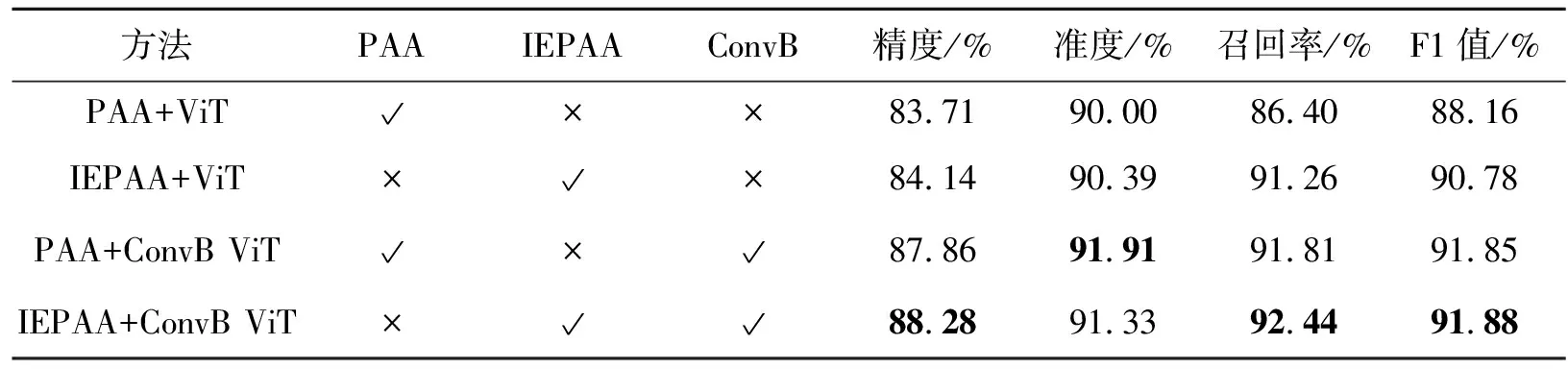
表4 各个模块作用

从表4中可以看出,基于不同配置的模型中,完整模型(IEPAA+ConvB ViT)与其他基线相比性能是最好的,其中精度、召回率、F1值分别达到88.28%,92.44%,91.88%,相对于基线模型(PAA+ViT)的精度、召回率、F1值分别提高了5.46%,6.99%,4.22%。虽然完整模型在准度方面不是最高(距最高相差0.58%),但是相对于基线模型也提高1.48%。同时通过比较不同的改进模块看出,ConvB模块相较于IEPAA方法在各方面的提升更为有效,前者在4个评价指标方面都相对后者上升更多。说明模型对于传感器数据的局部上下文信息更为敏感,通过对局部上下文的编码对模型效果提升更为明显。总之,T2D通过对PAA基于信息熵的改进以及在ViT中添加卷积映射是有效的,从总体趋势看引入新模块后,模型针对故障分类的性能提高显著。

2) IEPAA压缩维度影响

为了研究IEPAA数据降维的维度对模型性能的影响,在其他参数或者模块都保持不变的情况下,进行了一系列实验,实验过程中将降维后的数据维度从100～900分别进行对比实验,不同维度降维后实验结果如图7所示。

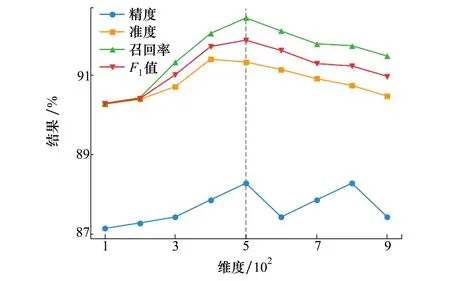
图7 不同降维维度结果图

图中,蓝色、橙色、绿色、红色分别代表精度、准度、召回率和F1值,其总体趋势大致都为先增加后减少。对于传感器的超长时间序列数据,如果数据降维的维度过短(例如图中100和200),其在降维过程中丢失的信息过多,过短的时间序列经过二维化之后形成的图片同样会丢失更多信息,因此模型不能更好地识别局部信息,导致模型的性能较差。然而,维度也不能过长,从图中可以看到在维度超过500时,各指标都出现下降,这是因为过长的维度在增加序列长度的同时,也带来了更多的冗余信息,其在经过二维化形成图片之后会增加更多不必要识别的局部信息,这可能会使模型学习更多不必要的知识,从而导致模型性能下降。总之,在经过充分的实验对比后,选择500作为IEPAA的降维维度,模型在此时表现最佳。

3) ConvB卷积核大小影响

ConvB内部的配置将会影响整个模型的性能,由于卷积核大小对卷积神经网络(CNN)的性能和特征提取能力有着显著的影响,例如较小的卷积核可以更好地捕捉细节和局部特征,而较大的卷积核可以更好地捕捉全局特征和模式;同时,卷积核的大小决定了每一层的感受野大小,其中较小的卷积核通过多次卷积操作可以增加感受野的范围,从而捕捉更大范围的信息,然而较大的卷积核可以更快地扩大感受野,但可能无法捕捉到更细节的信息。因此,在设计CNN时,通常会结合不同大小的卷积核,以便同时捕捉不同级别的特征。针对ConvB ViT编码器的卷积映射中不同卷积核大小进行了实验,其结果如表5所示。

表5 不同卷积核对比结果

表5给出上述具有不同卷积核大小的卷积映射操作结果,其中卷积核大小为3×3的卷积映射具有最佳性能,其精度、召回率、F1值分别达到88.28%,92.44%,91.88%。从结果来看,发现感受野过大过小都会降低模型的性能。前者可能会学习更多的上下文信息从而错过局部结构的信息,而对于某些故障区间较小的情况,这种模型表现不佳。对于后者来说,会丢失更大范围的特征,从而导致无法处理故障区间较长的情况。因此,本文选择卷积核大小为3×3的窗口以实现最佳性能。

2.4 可视化分析

为了更直观地验证对航空传感器故障检测任务中所提出的T2D框架的优势,本为采用了t-SNE方法[30]对原始数据、RNN、BBN、GTDA、T2D(IEPAA+ViT)以及T2D(IEPAA+ConvB ViT)多个方法进行可视化(如图8所示),并结合表3中的实验结果对T2D进行定性和定量分析。

图8 t-SNE可视化图

图8展示了试飞仿真数据集中5种算法的t-SNE可视化结果。图8a)显示了原始数据经过t-SNE转换后在二维空间中的分布,其中不同颜色的点表示传感器的不同状态(正常/故障)。图8b)～8f)中点表示意义与图8a)相同。在进行t-SNE可视化时,困惑度设置为10,学习率为100,迭代次数设置为1 000次。通过观察图8,可以发现T2D提取的特征相对于其他方法更为有效,其正常数据和故障数据能够直接地区分开,而且分离数量更为明显。结合表3可以看出,其对应各模型检测的精度,从数据上能够定量地解释可视化的结果。同时,T2D相比其他方法能够更好地捕捉故障数据,这对应其具有更高的召回率。

综上所述,通过可视化结果和定量指标分析,可以明确得出结论:所提出的T2D框架在航空传感器故障检测任务中表现最佳。T2D能够更好地分离故障数据,为航空传感器故障检测任务领域提供了一种有效的解决方案。这对于提升飞行安全性、减少事故风险具有重要意义,并为进一步研究和应用相关技术提供了有力支持。