考虑微元强度韦伯分布与裂纹长度幂律排布的砂岩强度预测模型
2024-01-03石浩张后全吴疆宇宋雷李明荣传新陆鹏举
石浩,张后全,吴疆宇,宋雷,李明,荣传新,陆鹏举
(1.安徽理工大学 矿山建设工程安徽省高校重点实验,安徽 淮南 232001;2.中国矿业大学 深部岩土力学与地下工程国家重点实验室,江苏 徐州 221116;3.中国矿业大学 力学与土木工程学院,江苏 徐州 221116; 4.安徽理工大学 土木建筑学院,安徽 淮南 232001;5.山东科技大学 省部共建矿山岩层智能控制与绿色开采国家重点实验室培育基地,山东 青岛 266590;6.中煤矿山建设集团有限责任公司,安徽 合肥 230000)
随着煤炭开采工艺的进步、机械化水平的提高以及信息技术的发展,以数字化、信息化为前提和基础的智慧矿山建设已经取得了阶段性进展;相信在不远的未来,我国必然会实现深部煤炭的无人化开采[1]。智慧矿山的建设对岩石力学特别是强度的准确判识要求极高[2],而岩石内部的各类损伤对其强度特性的影响占重要地位,是引起岩石强度离散的关键[3-6]。因此,为了保障智慧矿山的建设以及井下人员、设备的安全,有必要掌握岩石内部的各类损伤对其强度特性的影响规律。
目前,关于损伤缺陷影响岩石强度特性的研究已取得了十分丰硕的成果[7-27],并且根据研究对象的不同可分为2类。第一类研究主要针对岩石微元体强度劣化等微细观损伤缺陷[7-12]。此类研究基于自然岩石为非均质材料,认为其宏观破坏对应微细观破坏由量变到质变的过程[7,9]。专家学者多从唯象学角度出发,假定微元体损伤参量服从韦伯统计分布规律,基于D-P准则或M-C准则建立与温度、蠕变等特定工况相关的岩石损伤本构模型。相关成果对于丰富岩石损伤描述方法及揭示岩石损伤内在机制具有重要意义,但众多研究主要是基于理论方法开展的,重在分析韦伯分布参数对应力-应变关系(曲线)的影响[7-10,12]。在本质上所研究岩石试件仍以黑箱的形式存在,无法设定微元体强度或损伤参量的分布规律,导致理论分布假设的合理性得不到充分验证。第二类研究主要针对裂纹、裂隙等宏观损伤缺陷[13-27]。此类研究预制缺陷数量差异较大,多数研究预制缺陷数量小于4,也有少量研究预制缺陷数量成百上千。对于预制缺陷数量小于4的研究,研究者主要分析单个裂纹、裂隙的倾角、数量、位置、张开程度以及多个裂纹、裂隙的组合形式等对岩石强度的影响[13-19]。相关成果对于了解缺陷岩石的力学性能具有重要意义,但对缺陷信息(如倾角等)的设置过于理想,也导致研究结果的普适性较弱[20-22]。对于预制缺陷数量成百上千的研究,研究者通常注重对缺陷生成方法(包括概率分布或利用地层扫描和计算机信息提取相结合)的提出和改善[23-26],而对缺陷如何影响岩石强度特性的分析相对不足[25-26]。另外,裂纹长度服从幂律排布的规律也未被充分考虑。赵洪宝等[22]回顾了关于裂隙(纹)岩石的研究,指出应当考虑分布裂纹数量及裂纹间的相互作用并建立与裂纹分布相关的强度理论,才能真正提高研究成果的工程应用价值。以赵洪宝等人的观点作为指引,本课题组[27]根据Mori-Tanaka理论进行推导,首先建立了与预制裂纹分布信息相关的损伤砂岩强度模型。
鉴于自然界的岩石试件其内部宏细微观缺陷并存,仅对宏观或细微观的缺陷进行单独研究难以全面地掌握岩石承载失效特性,而目前统筹考虑岩石宏细微观缺陷对其强度特性影响的研究较少。因此,本文综合考虑岩石微元强度的韦伯分布与裂纹长度的幂律排布规律,采用数值模拟与理论推导方法分别构建损伤岩石试件的离散元计算模型与强度预测模型,并利用数值计算结果对理论模型的合理性进行验证。
1 岩石微元强度韦伯分布与裂纹长度幂律排布理论
1.1 岩石微元强度韦伯分布理论
岩石可视为由众多基元介质组成的有机整体,岩石破坏过程对应基元体损伤由量变到质变,基元介质的力学性质描述适用于统计的方法[7-9]。和众多专家学者的研究一致,本文假设岩石微元破坏的概率随微元强度F=f(σa)的分布密度P为[7]
P=[f(σa)]
(1)
式中,σa为试件的许用强度。
根据(1)式可得损伤度D与微元破坏的概率密度的关系为
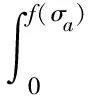
(2)
根据(2)式可知,确定岩石的微元强度与破坏概率是建立岩石损伤模型抑或岩石强度预测模型的前提。目前,韦伯函数已被证明适合用于描述岩石微元强度或损伤的统计分布规律[7-12],对应的岩石微元破坏概率密度方程为

(3)
式中:n,F0均为韦伯分布参数;n为均质系数,用以反映微元体强度等力学参数分布的密集程度;F0代表尺度参数。
1.2 岩石裂纹长度幂律排布理论
已有研究表明[25,27-28],岩石中的裂纹长度服从幂律排布,对应的分布方程为
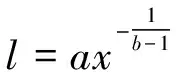
(4)
式中:l表示裂纹长度;x表示有关裂纹长度分布的自变量;另外,a为大于0的常数且a=zeta(1/b-1),而b为大于1的幂律指数。在实际应用中,需要预先给出预制裂纹的最大长度lmax、最小长度lmin和幂律指数b,从而确定特定的幂律排布形式。然后,根据(4)式的增减性可以建立(5)式所示关系
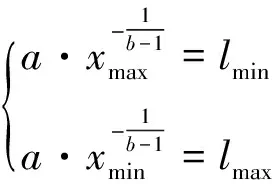
(5)
式中,xmax,xmin分别为x的上界和下界。另外,考虑到(5)式为超静定方程,a,xmin及xmax均为未知参数,需要提前给一个参数赋值,故假定(6)式成立
a=1或xmin=1或xmax=1
(6)
根据(5)~(6)式可以确定裂纹长度的幂律排布形式。在此基础上,通过给定预制裂纹数量n,具体的裂纹长度可以利用线性插值(理论)或概率分配(数值模拟)的方式获得。
2 考虑微元强度韦伯分布与裂纹长度幂律排布的砂岩强度模拟研究
无论是岩石微元强度的韦伯分布抑或裂纹长度的幂律排布,对其研究都难以通过室内实验开展,但理论模型的建立需有数据支撑。考虑到韦伯分布及幂律排布在本质上都是数学运算[7,27],完全可以通过数值方法编程实现,故在此采用数值模拟方法分析微元强度韦伯分布与裂纹长度幂律排布对岩石强度的影响。
2.1 颗粒黏结模型
PFC2D(particle flow code 2D)作为离散元颗粒流软件,被广泛应用于岩土力学方面的研究[27]。该软件优势契合本文研究主题,能够较好地模拟微元强度及裂纹长度等分布对介质模型强度的影响,故被本文研究选用。PFC2D软件对岩土介质的表征主要采用颗粒及黏结两部分,其中颗粒为刚体,通常用圆盘表示;而对于颗粒间的黏结,适用于岩石材料的模型主要有2种,分别为接触黏结模型和平行黏结模型,两模型对应的颗粒及黏结的力学行为如图1所示。接触黏结模型(见图1a))相对简单,仅能表征由颗粒接触、碰撞产生的法向力和切向力;而平行黏结模型(见图1b))既能反映颗粒间的接触作用,亦能反映颗粒间的弯矩作用。通常认为,此2种模型在岩石内部均存在[27,29-30],故本文研究采用包含这2种模型的颗粒黏结模型(PBM)。

图1 黏结模型及其微观力学行为示意图[27,29-30]
2.2 无初始损伤砂岩数值模型及细观参数的确定
研究岩石微元强度韦伯分布及裂纹长度幂律排布对其强度的影响,理想状态下需获取无初始损伤试件的强度特性[14,27]。但在现实条件下,所有可获得的岩石试件都不可避免地存在各类损伤且难以量化,专家学者一般选择无明显损伤的试件作为无初始损伤试件开展研究[14]。按照此种思路,笔者基于标准尺寸青砂岩的单轴压缩室内实验,在先前的研究中已经建立了相应的PFC2D数值模型并标定了模型细观参数[27]。模型参数已在表1中列出,本文研究均基于该数值模型及标定的细观参数。需要特别指出的是,所提青砂岩试件其单轴压缩实验强度约为52.22 MPa[27]。

表1 PFC2D介质细观参数[27]
2.3 微元强度韦伯分布与裂纹长度幂律排布的实现及数值计算结果
2.3.1 微元强度韦伯分布的实现
对于表1中列出的众多模型细观参数,用以控制微元强度的主要为黏结黏聚力及黏结拉伸强度[27]。所以对于数值模型微元强度韦伯分布的实现,仅需利用PFC2D软件自带的FISH语言编程生成特定形式的韦伯分布随机数,随机数数量与黏结数量相同,然后将韦伯分布随机数分别与黏结的黏聚力和拉伸强度同时结合(取乘积),生成新的平行黏结黏聚力及平行黏结拉伸强度数值。本文综合考虑均质系数n对Weibull分布覆盖区间范围及区间内分布梯度的影响,设置其值分别为1,1.5,3,5,7。通过对模型颗粒间的黏结信息进行统计,得到的颗粒黏结强度σb模拟与理论分布之间的对比情况如图2所示。可以看出,理论分布与模拟分布高度一致,颗粒黏结强度均呈减速降低趋势。并且,均质系数越小,颗粒黏结强度参数极大值越大;当均质系数为1,1.5,3,5,7时,对应的黏结强度参数极大值分别为401.79,172.87,74.38,53.08,45.93 MPa。另外,各均质系数下的曲线交汇点对应的黏结强度值为32 MPa,与表1中黏结强度值一致。

图2 颗粒黏结强度模拟分布与理论分布对比
2.3.2 裂纹长度幂律排布的实现
在PFC2D软件中,裂纹以构件的形式存在。长度服从幂律排布的裂纹是利用FISH语言编译软件中的DFN(discrete fracture network)模块生成的,具体步骤为:①设置裂纹的长度范围、长度分布形式、倾角范围、位置分布形式;②给定裂纹的数量以及在试件中的分布范围,由此生成裂纹;③赋值裂纹力学属性参数。本文设置的裂纹参数与文献[27]一致,裂纹长度范围为0.5~10 mm,服从幂律排布;倾角范围为0~180°;位置分布随机,分布范围与试件面积范围一致[31]。预制裂纹力学参数赋值基于平滑节理模型(smooth-joint model),模型参数已在表2中列出[14,27]。可以看出,裂纹存在的主要作用是破坏裂纹面两侧黏结的黏聚力和拉伸强度。

表2 平滑节理模型的力学参数[14,27]
温度应力、风化、开采扰动、海水侵蚀以及地质作用程度的不同都会对岩石损伤产生较大影响,导致其内部裂纹信息存在较大差异。基于此种考量,本文建立的数值模型根据预制裂纹数量及裂纹分布幂律指数可以分为4类。具体而言,预制裂纹数量分别设置为50,100,200,400,而幂律指数b分别设置为1.1,2,3,6,该参数同样是在考虑幂律排布的覆盖区间范围及区间内分布梯度变化的情况下确定的。当预制裂纹数量为50,预制裂纹长度lp在不同幂律指数下的理论分布与模拟分布对比如图3所示。可以看出,模拟与理论分布形式基本一致,均呈减速降低趋势。并且,幂律指数越小,裂纹长度降低速率越平缓(见图3中幂律指数为1.1对应的分布曲线),对应长裂纹占比越高;幂律指数越大,裂纹长度降低更接近于两段式,先急速降低再平稳变化(见图3中幂律指数为6对应的分布曲线),对应长裂纹占比越低。
2.3.3 数值计算结果
根据2.3.1节及2.3.2节可知,本文共计建立了5均质系数×4裂纹数量×4幂律指数=80个参数组合。为了尽可能降低试件强度离散性的影响,每个参数组合包含5个试件。需要指出的是,每个参数组合5个试件的所有参数信息都是一致的,但5个试件对应的微元强度韦伯分布模块及DFN模块调用次数分别为1~5。当微元强度韦伯分布模块及DFN模块调用次数一定时,试件内部的微元强度和裂纹分布信息是完全一致的,即试件的模拟计算是可重复的;而当调用次数变化时,微元强度和单个裂纹的实际存在位置及形式将再次发生随机分布[27]。由上述介绍可知,本文针对损伤岩石共计建立并计算了400个数值模型试件,基本能够实现对微元强度、预制裂纹信息及岩石强度间关系的统计研究[27]。
以预制裂纹数量np为x轴(第一维),均值系数n为y轴(第二维),幂律指数b为z轴(第三维),单轴抗压强度σ1c为颜色轴(第四维),根据模拟结果构建得到的试件单轴强度四维散点σ1c(np,n,b),如图4所示。可以看出,各参数组合试件1~5的强度分布规律基本一致,抗压强度最大值超过26 MPa,最小值接近1 MPa;另外,抗压强度具有明晰的定向流动规律,其最小值均对应预制裂纹数量较多、均质系数较小且幂律指数较小处,抗压强度最大值均对应预制裂纹数量较少、均质系数较大且幂律指数较大处。

图4 400个试件抗压强度模拟结果四维空间散点
3 考虑微元强度韦伯分布与裂纹长度幂律排布的砂岩强度预测模型
3.1 考虑微元强度韦伯分布的砂岩强度预测模型及验证
(2)~(3)式分别给出了损伤变量与微元破坏概率密度的关系以及岩石微元强度与破坏概率的影响因素。考虑到岩石最终破坏是损伤不断增加的连续过程所引发的结果,故将(3)式代入(2)式进行积分,得到了损伤度与微元强度概率间的对应关系为
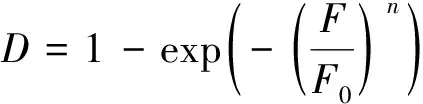
(7)
试件的有效应力σe与损伤程度的关系为
σe=σa(1-D)
(8)
式中,σa为无初始损伤试件的最大承载应力,数值上取为无初始损伤试件的单轴压缩强度[27],根据2.2节知该值为52.22 MPa。
根据F的定义,其数学期望值E(F)、标准差SD均可表示为n,F0的函数,为
式中,符号Γ为伽马函数,其在实数域上的定义为
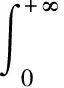
(11)
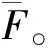
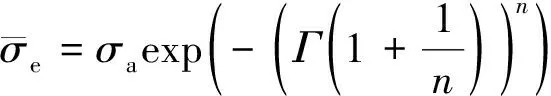
(12)
考虑试件强度的离散性及(12)式的增减特性,将实际应力矩阵以区间范围的形式表示为
(13)
实际应用中需要给出应力矩阵与均质系数之间的确切关系,如此便需确定方差系数。考虑到试件(非)均质离散性随均质系数的变化而变化,假定方差系数服从表达形式覆盖广泛的Logistic函数[3],由此可得实际应力矩阵与均质系数之间的关系
(14)
式中,ξ1,ξ2,ξ3和ξ4均为方差系数表达式的待定常数。
利用(14)式拟合模拟结果,如图5所示,可以看出将方差系数假定为均质系数的Logistic函数能够较好地描述有效应力随均质系数的变化规律,相关系数R2超0.999,说明该假定是合理的。并且计算可得,在n的变化区间内,ξ1,ξ2,ξ3和ξ4的组合数值介于-1~1之间,满足要求。
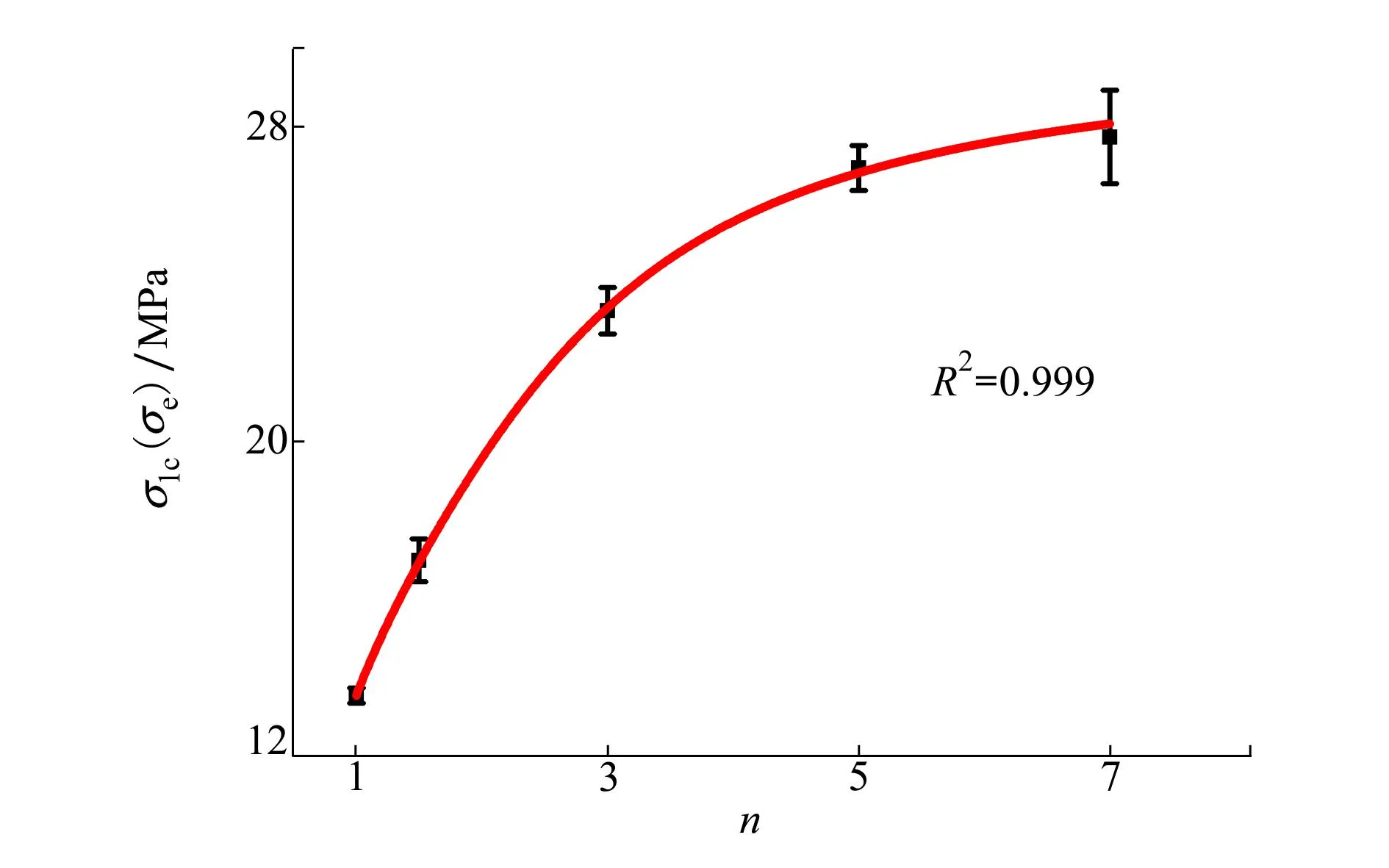
图5 理论与模拟得到的岩石抗压强度随均质系数的变化规律
3.2 微元强度韦伯分布与裂纹长度幂律排布耦合影响下的砂岩强度预测模型及验证
当仅考虑裂纹对试件强度的影响时,笔者已根据Mori-Tanaka方法建立了有效应力与裂纹密度之间的关系[27]
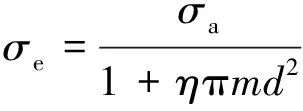
(15)
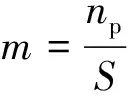
同样利用Logistic函数对文献[27]的数据进行回归,可得η和d与幂律指数b的关系分别为[32-34]
相关系数R2均超0.999。根据(15)式中单位面积裂纹数量m与预制裂纹数量n的关系以及裂纹平均半长d与幂律指数b之间的关系,可得有效应力σe与预制裂纹数量n及幂律指数b之间的关系为
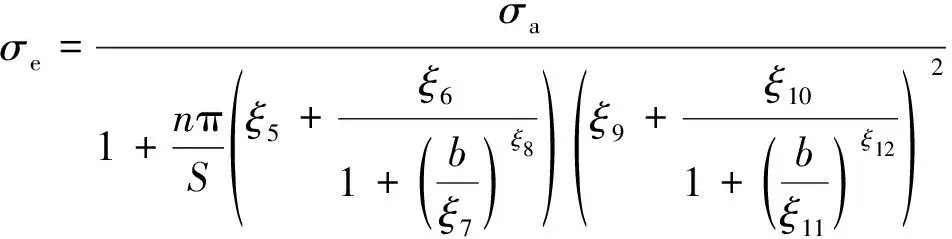
(16)
裂纹作为结构单元,其存在直接导致所在位置黏结的拉伸强度及黏结强度降低为0(见表2)。虽然裂纹对试件强度的作用在本质上也是通过影响(“杀死”)微元强度实现的,但其对黏结的破坏程度决定了受裂纹影响的黏结将可能不再受微元强度韦伯分布的影响,即裂纹与微元强度韦伯分布对黏结的影响互不干扰。据此,结合(14)及(16)式,叠加考虑微元强度韦伯分布及裂纹长度幂律排布对试件强度的影响,可建立12参数的砂岩强度预测模型为

(17)
结合图5的拟合结果以及文献[27]中的数据可得模型涉及的12个参数数值,在表3中列出。
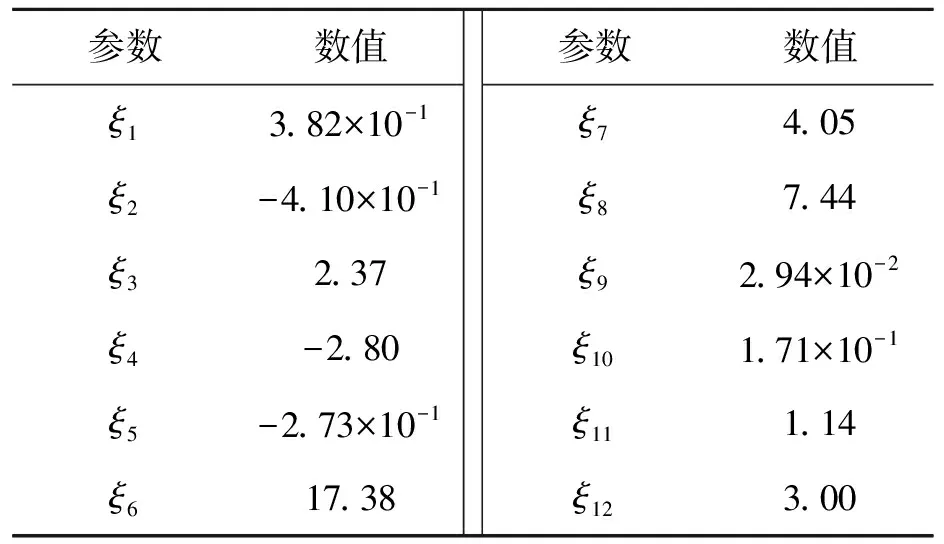
表3 砂岩强度预测模型参数数值
理论模型建立后,需要对其合理性进行验证。本文首先利用(17)式计算砂岩试件在不同预制裂纹数量、裂纹分布幂律指数及微元强度均值系数影响下的单轴抗压强度值,然后构建得到了砂岩单轴抗压强度理论值的四维空间散点,其与模拟结果平均值的对比如图6所示。可以直观看出,抗压强度理论分布(见图6b))与模拟分布(见图6a))基本一致,即抗压强度最小值均对应预制裂纹数量较多、均质系数较小且幂律指数较小处;抗压强度最大值均对应预制裂纹数量较少、均质系数较大且幂律指数较大处。
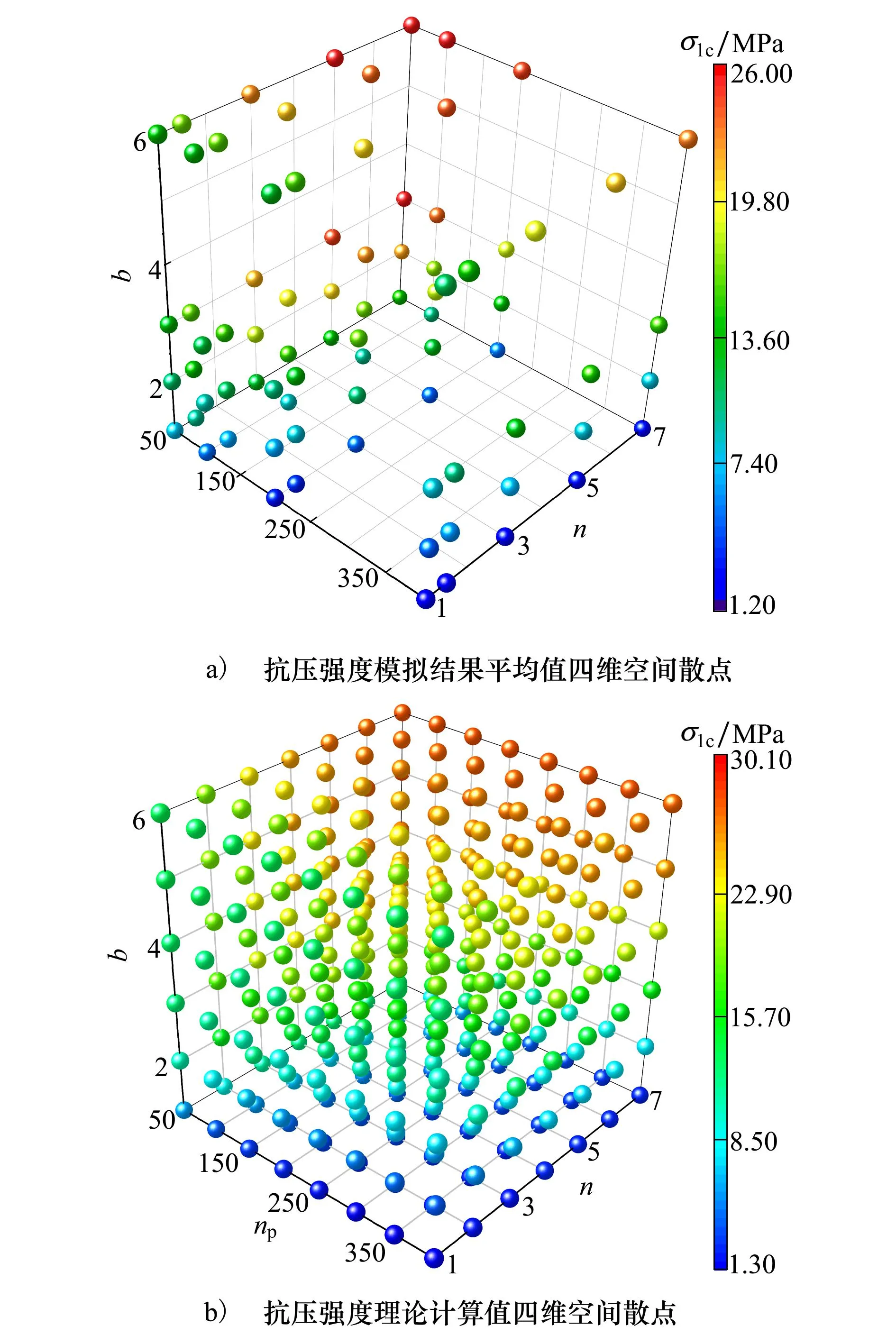
图6 抗压强度模拟结果平均值与理论计算值四维空间散点
上述是对理论结果与数值结果分布相似性的主观描述,为了定量描述理论结果与模拟结果的吻合程度,依照数值模拟设置的参数组合,利用(17)式计算获得了砂岩试件在相应预制裂纹数量、裂纹分布幂律指数及微元强度均值系数影响下的单轴抗压强度,其与模拟结果平均值对比如图7所示。图中,横坐标表示80个参数组合按照所得砂岩强度模拟均值自小至大依次排列时对应的序号。可以看出,理论结果与模拟结果高度一致,并且计算得相关系数R2=0.991,说明利用所建强度预测模型能够较好地描述微元强度韦伯分布与裂纹长度幂律排布对试件强度的影响。
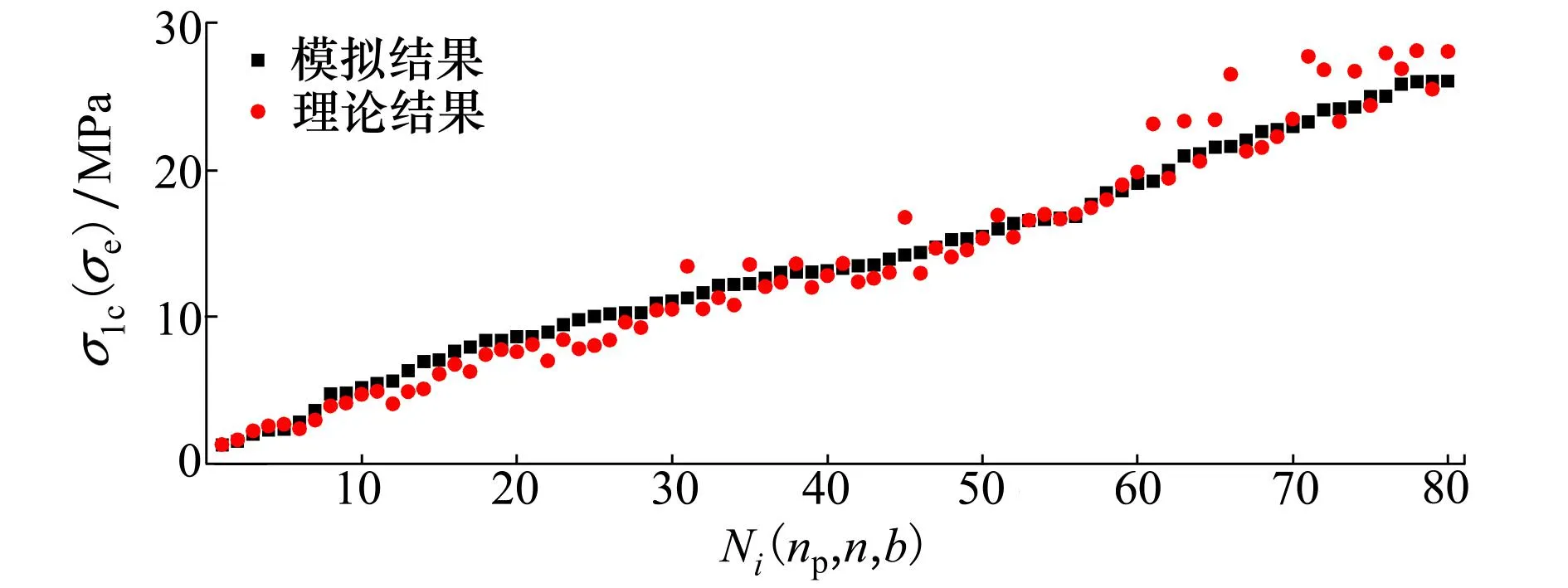
图7 理论计算值与模拟数据的对比
4 结 论
本文综合考虑岩石微元强度的韦伯分布与裂纹长度的幂律排布规律,构建了损伤砂岩试件的PFC2D计算模型及强度预测理论模型,并利用数值计算结果对理论模型的合理性进行了验证。主要结论为:
1) 通过编程同时实现了PFC2D计算模型中微元强度的韦伯分布与裂纹长度的幂律排布,分析了岩石中的宏、细微观损伤与相应分布参数间的定量对应关系。
2) 数值建立了400个同时考虑宏、细微观损伤的砂岩试件并对其进行了模拟加载,实现了对微元强度、预制裂纹信息及岩石强度间关系的统计分析。根据模拟结果构建了砂岩试件单轴抗压强度四维空间散点σ1c(np,n,b),得到了多损伤参量影响下的试件抗压强度流动规律。
3) 联合Mori-Tanaka方法及岩石损伤概率分布理论,推导建立了12参数的岩石强度预测模型,经与数值模拟结果对比分析,该模型被证明能够有效地描述细微观微元强度及宏观裂纹信息对岩石强度的影响。
