一种机扫超视距侦测系统测向模型及其解算方法

2024-01-03綦韬,陈宇

雷达与对抗 2023年4期

綦韬,陈宇

(中国船舶集团有限公司第八研究院,南京 211153)

0 引言

在不发射对目标照射电磁波的条件下,无源侦测系统通过测量雷达、通信等发射机(辐射源)的电磁波参数来确定辐射源及其携载平台或目标的位置信息和航迹,因而具有作用距离远、隐蔽性好等优点,对于提高系统在电子战环境下的生存能力具有重要作用[1]。

超视距侦测系统[2]由于其特殊机理,可实现对海上目标的远距离侦测,对目标远程预警具有重要意义。对于超视距侦测,提高辐射源目标测向精度的重要性不言而喻,尤其是运动平台的测向精度,将直接对目标的交会定位产生很大影响。其中机械扫描方式工作的超视距侦测系统受到收发双发天线方向图和天线扫描的调制,因此在采用最大幅度法进行测向时往往存在测向模糊[3]。

针对上述问题,本文建立一种机械扫描超视距侦测系统测向模型,并利用窗口截获理论[4]分析其截获和测向特性,给出其解算方法和一种变扫描周期进行解模糊的测向策略,最后通过仿真验证了方法的有效性。

1 超视距侦测测向模型

超视距侦测系统对目标的侦测场景如图1所示。

图1 超视距侦测示意图

对上述场景做出如下假设:

(1)假定侦测系统扇扫角度范围为[θmin,θmax](本文角度均以正北为基准),初始扫描方位为θ0,扇扫速度为v0;

(2)侦测系统能够探测到目标的范围为 [θ-θB/2,θ+θB/2],其中θB为侦测系统能收到辐射源的波束宽度,其大小与侦测系统天线方向图、侦测系统接收机灵敏度、目标天线方向图、目标辐射功率等均有关,在实际侦测时上述各种因素的综合作用会使其数值在每次截获过程中都稍有不同,左右亦不一定对称,后续将重点探讨;

(3)目标在侦测系统的方位为θ,天线环扫,初始方位为θT0,扫描速度为vTθ,天线的波束宽度为θTB,(θTB的定义与θB含义相同)。

上述雷达对辐射源目标的截获过程可用数学模型描述:

辐射源目标可被侦测系统截获的时间满足条件:

(1)

式中:ln为辐射源目标相对于起始时间扫描的圈数。

由式(1)得到目标可被截获的持续时间为

(2)

相邻两次辐射源目标可被截获的时间间隔为

(3)

侦测天线可截获到辐射源目标的时间满足条件:

(4)

式中:k=1,2,3,…。

由式(4)得到目标可被截获的持续时间为

(5)

相邻两次辐射源目标可被截获的时间间隔为

(6)

根据窗口函数理论对目标进行截获,当同时满足式(1)和式(4)条件时,发生目标截获。可见目标截获呈现出特定的周期规律性,利用该周期性尽可能精确地估计出辐射源目标的方位,是解决高精度测向问题的一个可能的技术途径。

2 超视距侦测截获与测向分析

2.1 理想截获

为了简化问题,忽略辐射源目标天线的这种转动,即假定辐射源目标一直对准侦测系统照射,分析此种理想情况下的解算方法。

式(4)～(6)没有考虑目标位置θ,实际上θ可能位于天线扫描的边界,式(4)～(6)可能需要进行相应的修正。

2.1.1 侦测天线可截获到辐射源目标的范围全部在扫描范围内

(1)不考虑侦测天线方向图

在此种情况下,若不考虑辐射源目标天线的转动以及侦测天线的天线调制特性,可用式(4)～(6)表述截获情况。由式(6)可根据目标的两次截获间隔,并利用下式估计目标方位:

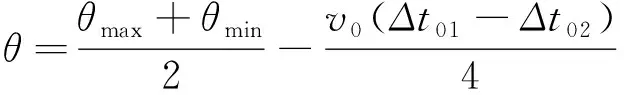
(7)

图2给出了式(4)～(7)描述的截获情况的时间轴,其中网状长方形为截获驻留时间。

(2)考虑侦测天线方向图

若考虑侦测天线的天线方向图调制特性,主瓣截获和主副瓣同时截获分别如图3(a)、(b)所示。

图3 考虑侦测天线调制特性时的截获时间轴示意

此时,若侦测天线的方向图左右对称,以及式(6)依然能描述目标的截获特性,则仍可按照式(7)估计目标方位;若侦测天线方向图左右不对称,则式(6)可以修正为

(8)

式中:θCenter-θl为天线左边波束边缘到波束中心的角度;θr-θCenter为波束中心到右边波束边缘的角度。

依据上述方法,式(7)可以修正为

式中:右边第3项为相对于式(7)的修正量,当天线方向图左右不对称时,表现为对测向方位的修正。

考虑到天线的机械、物理惯性,在旋转到天线边界回扫过程中会出现扫描速度先下降到0,然后上升到v0的现象,从而带来相应的时间停留或延迟。假定在天线顺时针和逆时针扫描过程中该驻留时间分别为τ1、τ2,则式(9)可修正为

(10)

式中:右边第3、4项均可以作为系统误差进行修正。

当信号幅度强弱变化时,天线方向图的不对称性亦会发生变化,对式(10)的右边第3项产生影响;同时,机械扫描过程中的回程差往往存在一定的差异,进而导致第4项存在一定的误差,因此式(10)所示的测向方法也会有相应的误差。

2.1.2 侦测天线可截获到辐射源目标的范围部分位于扫描范围下边界内

此时式(6)中的θmax-(θ+θB/2)<0,式(6)、式(7)可分别修正为

(11)

θ=v0Δt02/2+θB/2+θmin

(12)

式(12)右边第二项随信号幅度、前端衰减控制等发生变化,该种测向方式偏差较大,应调整天线的扫描范围,以覆盖辐射源目标的整个方位,转化为2.1.1节的情况进行分析。

2.1.3 侦测天线可截获到辐射源目标的范围部分位于扫描范围上边界内的情况

此时式(6)中(θ-θB/2)<θmin,式(6)、式(7)可分别修正为

(13)

θ=θmax+θB/2-v0Δt01/2

(14)

式(14)右边第二项与式(12)类似,此时亦应转化为2.1.1节的情况进行分析。

2.2 相互调制

当辐射源目标处于环扫状态时,其截获情况可用式(1)～(3)描述。考虑到辐射源目标的扫描速度vTθ一般较大、波束宽度较小,因而可被截获的持续时间τsT=θTB/vTθ通常较小,远小于1 s。而两次辐射源目标可被截获的时间间隔ΔtT=2π/vTθ一般在秒量级。

对图3所示的截获时间轴示意图进行调制,结果如图4所示。可以看出:辐射源目标与侦测天线的相互调制导致每次截获到的辐射源方位左右抖动,对接收到的辐射源目标幅度、方位等的简单加权处理很难克服上述调制引起的测向误差。

图4 考虑相互调制时的截获时间轴示意图

一种最简单的处理方法是对信号进行前端衰减,减小侦测天线截获到目标的角度范围,则可从一定程度上提高测向精度,但该方法会降低对信号的截获概率;另一种方法是降低侦测天线的扫描速度,增加对目标的截获次数,从而达到提高测向精度的目的。

辐射源目标天线的旋转导致目标截获时间差出现波动,此时若直接利用式(10)的方法,会带来较大的误差。细致分析式(10)的测向误差后可知,上述调制特性对式(10)右边第二项v0(Δt01-Δt02)/4的影响最大。由于海面目标运动较慢,可对式(10)中的两次截获间隔Δt01与Δt02进行相应的平滑处理,以提高目标的测向精度。

下面分析截获过程中的传输特性。假定在第1个周期中目标首次被截获的时间为t0,Δt01、Δt02、τsT含义与前文一致,则得到以下目标截获特性关系:

目标首次截获时间满足

(15)

目标最后截获时间满足

(16)

由式(15)有

(17)

由式(16)、(17)有

ts(i+1)-tei=

(18)

上述式中与Δt01、Δt02存在偏差,导致测向有误差。令τsT-t0=m1T+α1T,Δt01=m2T+α2T,Δt02=m3T+α3T,其中m1、m2、m3为非负整数,0≤α1<1,0≤α2<1,0≤α3<1。首先分析i的各种情况。

(19)

对于式(19),有0≤α1+α2<2。

(20)

令t0=β1T,0≤β1<1,有

(21)

令2α1+α2+β1=k+β2,k为非负整数。

(22)

综合式(20)、(22),有

(23)

可以看出:(ts3-te2)-(ts2-te1)基本呈现上述3种取值,而Δt01-Δt02=(m3-m2)T+(α3-α2)T,意味着利用式(23)计算目标的方位存在一定的误差,只有当α3=α2时没有误差。

(m2+α2)+(m3+α3)]⎤-⎣m1+α1」+

(24)

[2(m1+α1)+(m2+α2)+(m3+α3)]-

⎣2(m1+α1)+(m2+α2)+β1+[2(m1+α1)+

(25)

式中:2(m1+α1)+(m2+α2)+(m3+α3)为2个天线扫描周期时间除以辐射源扫描周期的倍数。

若目标多次截获过程中获取的时间差序列为{Δt1,Δt2,Δt3,…,Δtn},其中Δti为第i+1次初始探测到目标时刻与第i次最后探测到目标时刻差,则有Δti=ts(i+1)-tei。

考虑到海面目标运动速度较慢,在较短时间内上述时间差序列应该满足关系Δti=Δti+2。目标相互调制使得上述关系遭到破坏,体现为Δti=Δti+2+k*ΔtT(k为整数),其中ΔtT=2π/vTθ为辐射源天线扫描周期。同时,目标可被截获的持续时间τsT=θB/v0也可能被侦测天线的调制所切割,引起测时误差,考虑到τsT一般较小,可以忽略。因此,式(10)测向算法主要误差可表示为kΔtTv0/4,可理解为超视距侦测的测向模糊。对Δt01与Δt02进行平滑处理,对于相邻两次的Δti、Δti+2,去掉kΔtT的模糊度,并对时间差进行平滑,提高对目标的测向精度。

从去模糊的角度出发,改变天线的扫描速度,则下式成立:

(26)

将式(26)表示为模糊度方程:

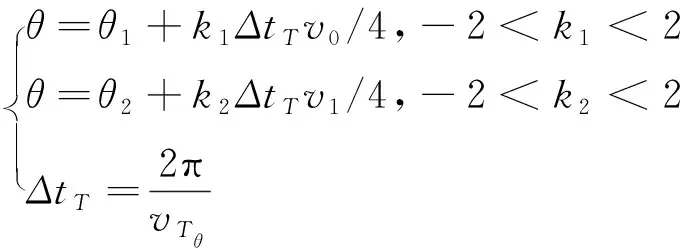
(27)

在式(27)解模糊后,能够较好地实现对目标的测向。

综合上述分析,可得到两种解模糊的测向算法,如图5所示。

图5 考虑相互调制情况下测向算法

3 仿真分析

为了验证上述测向算法,构建如下仿真场景:超视距侦测天线扫描中心为70°,扫描范围为22.5°,扫描速度为1 °/s,可截获到目标的波束宽度为10°;目标方位为75°,扫描速度为90 °/s,目标可被截获波束宽度为2°。

图6给出了侦测天线与目标随时间的方位变化,图7给出了上述天线转动过程中的截获示意。可以看出:由于侦测天线与目标天线的相互调制作用,出现了如图4所示的截获特性。上述截获特性广泛存在于各类超视距侦测系统中。

图7 目标截获方位时间图

图8给出了利用首尾求平均、截获时间差测向、相邻间隔截获时间差去模糊平滑测向等方法的测向结果。可以看出:由于侦测天线与目标天线的相互调制作用,首尾求平均测向法体现为波浪线式的1.5°上下起伏;截获时间差测向法能够较精确地解算出辐射源目标方位,但出现kΔtTv0/4=(-1)*4s*1(°/s)/4=-1°的测向模糊;相邻间隔截获时间差去模糊平滑测向法能够去掉一部分测向模糊,但还是存在一定的模糊。后续可以考虑用最小间隔法去掉所有模糊后进行测向。