应用功率谱法进行电磁阀线圈松动非线性模态仿真

2024-01-03廖云龙吴佩沛

火箭推进 2023年6期

廖云龙,吴佩沛,尤罡

(1．上海空间推进研究所,上海 201112; 2．上海空间发动机工程技术研究中心,上海 201112)

0 引言

空间推进系统设计领域广泛使用具有螺纹连接、箍带连接的结构,易出现非线性模态问题,如推进系统用电磁阀、气瓶、管路组件会因螺纹、箍带松动造成模态频率降低。航天产品对力学环境条件较为敏感,而非线性模态缺乏成熟的仿真方法,这一矛盾使得非线性模态机理研究愈发迫切。如何进行非线性模态仿真,成为空间推进系统设计过程中亟待解决的问题。

非线性模态研究发展过程中,Rosenberg的工作具有重要意义[1-2]。Rosenberg 于20世纪60年代初,在对非线性系统的自由振动进行研究时引入了非线性模态的概念。20世纪90年代,Shaw等提出了阻尼非线性模态,将相空间的不变流形定义为非线性模态,系统初始状态符合某一非线性模态,随后按照该模态运动[3-4]。刘鍊生等推广了相似模态的概念[5-6],使其能够应用于非线性系统。李诚等提出基于谱单元的伽辽金法求解不变流形定义下的非线性模态曲面,获得两自由度非线性系统更高精度的非线性模态曲面解[7]。胡晓君应用混合摄动伽辽金法进行单自由度体系的非线性随机结构自由振动数值分析[8]。近20年来,非线性模态理论发展仍停留在简单自由度系统分析阶段。

非线性模态分析由于其复杂性,使其长期处于理论研究状态,工程实际多采用模态试验与线性模态仿真结合的方法。代鹏等进行了脉冲等离子推进系统模态分析和试验验证[9]。杜大华等进行了火箭发动机涡轮盘模态影响因素与振动安全性分析[10]。田彤辉等研究了冲击荷载下级间螺栓法兰连接结构失效实验与数值仿真[11]。

直接应用非线性理论进行模态仿真存在困难,但模拟试验过程通过功率谱对系统动态参数进行识别,将瞬态仿真方法与信号分析方法相结合,可能成为解决非线性模态问题的另一种途径。功率谱密度(power spectral density,PSD)分析法应用于系统参数识别始于文献[12]。在时变系统或非线性系统参数识别相关研究领域,张洁等进行了机械变速过程的瞬时参数识别及频谱分析[13];王豪等应用图像处理技术,提出一种自适应时频脊线的方法,对时变结构在随机激励下的瞬时频率进行了辨识[14];王晓敏等研究了在白噪声激励下非线性声学超材料的随机响应[15];许文峰等研究了具有非线性刚度边界的杆梁结构的动态特性[16]。传统研究认为瞬态时域仿真应用存在计算量大、求解过程慢、数据处理过程复杂等问题,但近年来随着计算机能力的快速提升,基于瞬态时域法与信号后处理进行动力学仿真在多场景下已具备工程应用条件。聂肇坤等对运载火箭舱段连接结构进行了简化建模,采用冲击、周期信号时域非线性仿真,对时域结果进行FFT变换后与精细模型进行了对比验证,使得简化模型在保留线性计算效率的同时接近精细模型的计算精度[17]。乐晨等进行了运载火箭大直径螺栓承受拉弯耦合载荷的失效判据研究[18]。

基于计算机能力的提升与功率谱在模态试验中应用的优势,本文提出一种全新的瞬态动力学仿真与功率谱密度分析结合的方法,应用于空间推进系统电磁阀线圈螺纹松动非线性模态仿真。在时域进行接触非线性仿真,并将时域结果变换为功率谱,在频域进行非线性模态分析,关注重点为接触非线性对模态频率的影响。

1 时域随机试验条件拟合

某型号电磁阀是推进系统关键组件,线圈元件通过外套螺母连接于电磁阀本体,飞行试验过程中因随机振动导致线圈松动,出现模态偏移,本文以该阀门为研究对象,采用功率谱分析法进行非线性模态仿真方法研究。阀门随机试验条件以PSD形式给出,如表1所示,随机试验状态如图1所示。

图1 电磁阀振动试验Fig.1 Solenoid valve vibration test

表1 随机试验条件Tab.1 Random test conditions

采用随机试验条件作为结构的激励条件,可在较短的计算时间内激发结构多阶模态响应,相较正弦扫描等试验条件更适用于时域仿真分析。但应用随机试验条件进行时域仿真需要对PSD进行时域拟合,拟合出的随机试验条件具备相同的统计性质,但并不唯一。随机瞬态动力学分析首先需要进行时域随机数据拟合方法研究。

在现代信号分析中,PSD分析是研究具有时不变、各态历经、平稳随机信号的重要途径,PSD可反映随机信号各频率成分功率的分布情况,反映各阶模态的共振效果。随机信号的研究往往需要转换到频域进行,而理论随机信号通常是无限长的,需要使用有限长信号对真实PSD进行估计。经典谱估计方法包括维纳-辛钦定理、周期图法、Welch法等,其中周期图法为应用广泛且最具代表性的方法,其基本原理是对观测到的数据进行快速傅里叶变换(fast Fourier transform,FFT),然后取模的平方作为真实PSD估计。

取平稳随机信号X(n)的有限个观察点X(0),X(1),…,X(n),则傅里叶变换过程为

(1)

周期图法功率谱为

(2)

瞬态动力学仿真计算量较大,仿真时间较长,应在满足仿真需求的前提下尽量减少仿真资源的使用,减少仿真时间。随机条件最低频率为10 Hz,保证10倍最低频率采样,拟合总时长1 s。

对随机试验条件进行时域数据拟合与验证过程如图2所示。

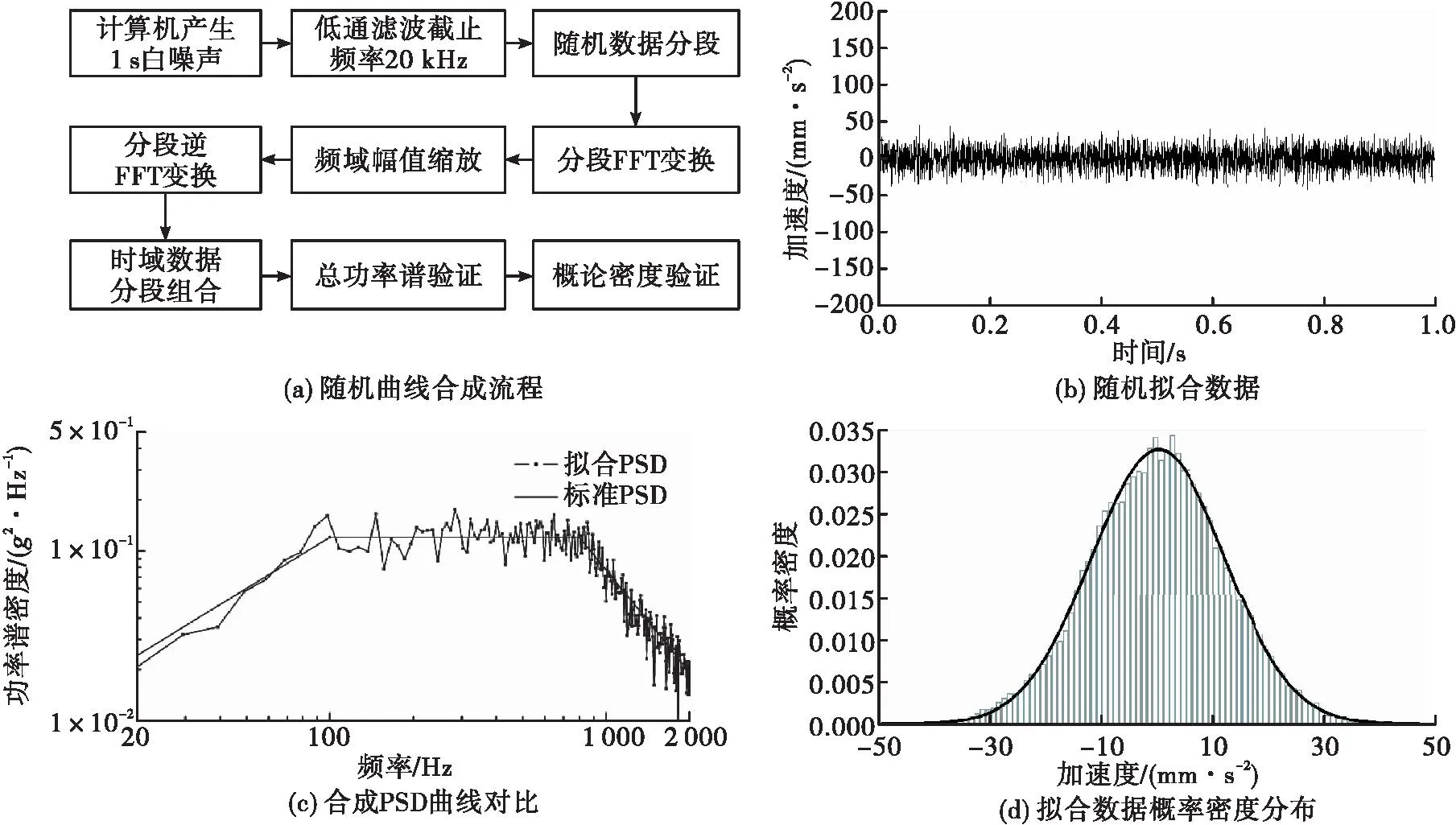
图2 时域随机条件合成流程Fig.2 Time domain random conditional synthesis process

依据图2(a)流程进行拟合验证,首先由计算机生成两列1 s均匀分布的白噪声UN、VN,应用文献[19]的方法获取正态分布的数据列XN,即

(3)

将数据通过截止频率为随机振动条件最高频率10倍的低通滤波器;对XN进行FFT变换后在频域进行增益调整,并采用周期图法进行PSD计算,使其符合试验曲线,再进行逆FFT变换,拟合的时域信号如图2(b)所示。

图2(c)为拟合时域加速度PSD曲线与标准PSD曲线对比。对拟合时域数据进行概率密度统计[见图2(d)],表明拟合数据具备较好的正态分布特征。在时域对拟合数据进行数学期望与均方根计算,如表2所示。其中时域数据数学期望接近0,均方根为12.2g,与表 1试验条件均方根加速度符合较好,作为后续瞬态动力学仿真的输入。

表2 数据统计性质Tab.2 Statistical properties of data

2 非线性模态仿真方法

2.1 模态仿真对比分析流程

为分析应用瞬态动力学方法进行非线性模态分析的有效性,同时进行非线性瞬态动力学模态仿真与基于线性模态叠加法的随机振动仿真。由于计算原理不同,仿真将依据不同的流程,如图3所示。瞬态动力学仿真过程使用拟合的随机时域条件作为输入,并将结果转换为PSD曲线;而线性随机仿真首先进行线性模态仿真,然后直接应用模态叠加法计算PSD曲线。

图3 PSD仿真对比流程Fig.3 PSD simulation and comparison process

2.2 非线性模态仿真

电磁阀线圈出现非线性模态的主要原因在于固定螺纹松动,能否在仿真方法中考虑螺纹松动过程出现的接触非线性,从仿真原理上考虑接触对模态结果的影响,是决定非线性模态仿真方法是否可行的关键。

基于瞬态显式动力学分析结果进行非线性模态仿真,在时间维度上进行迭代求解。瞬态显式动力学计算原理为应用中心差分法对物体运动过程进行积分,其迭代求解的基本方程如式(4)与式(5)所示。

(4)

(5)

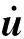
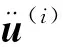
(6)

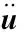
瞬态动力学计算过程中,式(6)中质量矩阵、外力向量、内力向量均进行修正,且任意迭代步均可以考虑接触非线性影响,进入接触范围的节点可依据摩擦因数进行力的传递。当内力I(i)与外力F(i)不平衡时,接触对将发生滑动,出现接触非线性。

采用瞬态动力学方法,应用商用有限元软件ABAQUS将拟合的时域试验条件作为动力学仿真输入条件,对阀门进行时域振动仿真。边界条件与假设如下。

1)考虑阀门线圈螺杆与螺母螺纹之间为接触关系,在模型上引入接触非线性。

2)建立虚拟梁单元两端分别与阀体垫圈端面、螺母端面耦合约束。

3)旋紧线圈螺杆时,螺纹发生接触,螺杆产生位移压缩梁单元,虚拟梁内力即反映螺纹预紧力,通过预紧力试验与螺母旋松旋紧仿真,对螺纹摩擦因数进行精确标定。

电磁阀上提取3个响应点时域数据,位置如图4所示。

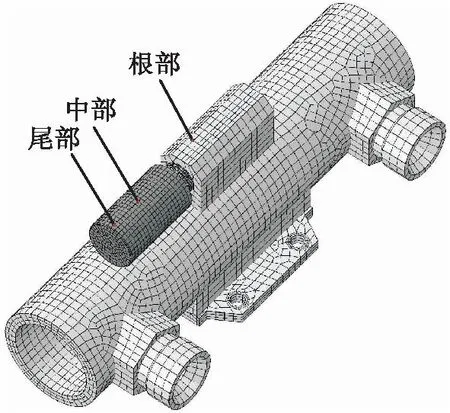
图4 线圈模型Fig.4 Coil model

图5为经过1 s时域随机载荷瞬态动力学仿真后得到的预紧力时域曲线,预紧力由19 kN减小到3.6 kN。预紧力的减小使得结构整体的刚性减弱,整体模态频率降低。

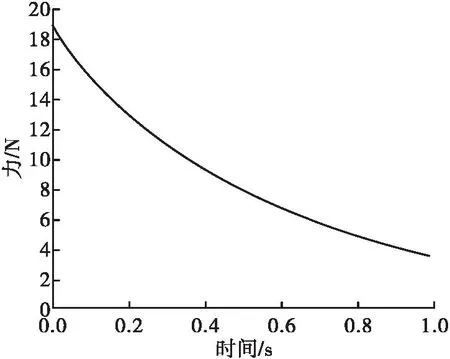
图5 预紧力时域曲线Fig.5 Pre-tightening time domain curve

瞬态动力学仿真结果包含所有节点的时域曲线,如图6所示,提取线圈根部、中部、尾部3个响应点时域响应曲线,可见从线圈根部到线圈尾部,加速度响应呈现放大趋势。

图6 测点时域加速度响应Fig.6 Time domain acceleration response of measured point

2.3 线性模态仿真

基于对比分析的需求,应用商业有限元软件ABAQUS同时进行线性模态仿真。线性模态仿真基于特征值法,结构自由振动方程为

(7)

式中:C为阻尼矩阵;K为刚度矩阵。

自由振动位移u的振动属性为

u=φejωt

(8)

模态计算过程中忽略阻尼C,并考虑式(8),则式(7)转化为

(-ω2M+K)φ=0

(9)

式中ω为结构圆频率。求解模态的过程即求解广义特征值与特征向量。

数值方法求解特征值过程中,式(9)中无时间相关量,即质量矩阵与刚度矩阵为确定状态同时求解多个特征值,从原理上无法考虑与时间相关的非线性影响,即特征值法无法进行接触非线性模态分析。

对阀门线性模态仿真过程中,采用如下边界条件。

1)假定螺纹为完全约束状态,即不存在松动、接触。

2)结构属性不变,即结构不出现屈服等材料非线性性质。

图7为应用线性法得到模态振型,振型描述了特征值对应的特征向量。

图7 阀门线圈模态振型Fig.7 Modal vibration of valve coil

2.4 结果分析

模态频率对比如表3所示。非线性时域仿真反映出螺纹逐渐松动过程中,预紧力逐渐变小,结构整体刚性变差,导致模态频率降低的结果,模态仿真频率为1.464 kHz;线性随机仿真进行保守假定,即认为螺纹为完全固定状态,反映在仿真结果上模态频率更高,模态仿真频率为1.576 kHz。如图1所示,推进系统振动试验过程中,电磁阀线圈出现松动,线圈头部加速度峰值频率约为1.450 kHz。

表3 模态频率对比Tab.3 Comparison of modal frequency

将非线性仿真方法与线性仿真方法结果进行对比分析。将瞬态动力学线圈根部、中部、尾部响应曲线依据周期图法转换为PSD曲线,如图8(a)所示。图8(b)为使用模态叠加法获得的线圈相应位置PSD曲线。将曲线对比可以发现,线性与非线性PSD曲线形态相似,均反映主振模态特征,区别在于瞬态动力学采用的时域方法考虑了螺纹松动接触非线性影响,计算频率低于线性模态仿真方法。

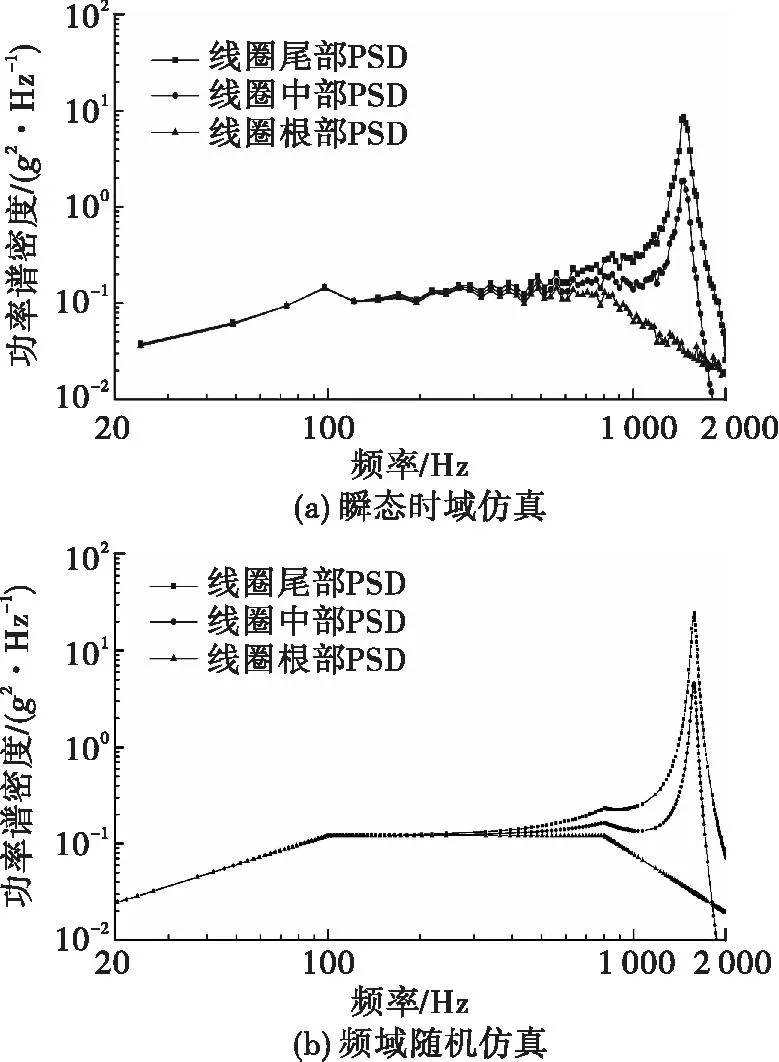
图8 PSD仿真结果对比Fig.8 Comparison of PSD simulation results

值得说明的是,本文提出的非线性模态仿真方法无法获取系统模态振型,但由于线性、非线性方法获得的频率峰值接近,工程仿真过程中将线性模态振型作为参考。

图8(a)的非线性仿真方法模型中使用预紧力试验标定过的摩擦因数,计算过程中考虑了接触非线性,最终得到模态非线性仿真结果;而图8(b)线性仿真方法无法考虑螺纹副接触状态,采用保守的全固定约束方式,得到保守的线性仿真结果。

虽然线性算法可假定部分螺纹固定,将模态仿真结果标定至试验值,但全固定至部分固定变化规律缺乏理论与物理事实依据,仅可做经验性假设,而这一关键性假设对仿真结果影响较大,除完全固定与完全不固定两种极限状态外,无法证明其余状态下仿真结果偏保守或者激进。相较而言,在本文采用的非线性仿真方法中,对仿真结果存在影响的摩擦因数具备明确物理含义,可采用预紧力试验进行标定,使用标定参数进行仿真,得到更为接近试验值的仿真结果。

本文采用的非线性模态仿真方法理论上可推广应用于包括材料非线性、几何非线性、边界非线性等在内的非线性模态分析。