基于扩展二相杂交应力有限元法的两相材料界面裂纹断裂力学分析

江海涛, 李欢, 杨文彩

(云南农业大学机电工程学院, 昆明650201)

随着科学技术的发展,层状复合材料或结构如复合材料层合板,因其比强度及比模量高、抗疲劳断裂性能好等良好的力学性能在航空和电子等一些重要工业领域得到广泛的应用。实际应用过程中,由于复合材料界面两侧各相材料性能各异,以及制造过程中存在的缺陷,在外载荷的作用下,结构断裂产生的裂纹通常发生在界面处,界面裂纹的扩展也是降低复合材料性能的主要因素之一。例如,基岩和混凝土坝之间在外力的作用下,界面处产生大量初始微裂纹,进而扩展相交形成宏观裂纹,最后扩展贯通导致结构失效。因此,对于界面裂纹的分析研究对优化复合材料,提高其应用性能及可靠性是十分重要的。

研究裂纹扩展的方法分为理论、实验以及数值模拟,对于实际环境中材料的应用,为更准确地观察测量裂纹的产生和裂纹尖端附近应力场以及应变场,在边界条件和几何条件下数值计算方法更加有效,具有更高的适应性和精确性。有限元法是数值计算中最可靠、应用最普遍的方法。在有限元方法中,对于裂纹的研究依赖于计算网格的划分,在裂纹扩展过程中,计算网格要与裂纹的几何形状一致,并随裂纹的每一步扩展重新划分网格。Williams[1]研究了各向同性双材料界面裂纹,结果表明界面裂纹尖端附近位移场和应力场具有振荡奇异性。由于其振荡行为,对各向同性双材料界面裂纹进行建模采用针对均匀材料的传统求解程序已经不充分,即使在裂纹尖端附近使用非常细的网格来捕捉界面附近的高梯度和奇异性的应力应变场,单元公式中没有包含高阶奇异项,精度没有太大提高,导致收敛性极差。

为解决传统有限元方法中的问题,Gao等[2]采用扩展有限元法(extended finite element method, XFEM)研究了各向异性断裂韧性材料中的裂纹扩展行为。该方法在研究复合材料层合板时,成功地用于预测复合材料中典型的复杂裂纹场景。例如,分层模拟[3-6],微尺度模拟[7],多尺度模拟[8]和基体裂纹/分层相互作用[9-10]。在数值分析中裂纹面不必再与单元界面重合,但由于裂纹尖端附近节点和自由度的增多,计算成本提高,而且基于位移的扩展有限元法其单元模式还是低阶位移单元,收敛性还是不好。1960年初期,对于固体结构的有限元分析都是以单元节点位移为未知数,根据势能原理协调元或余能原理平衡元构建刚度矩阵。Pian[11]根据余能原理假定单元内部平衡的应力和相邻单元间协调的边界条件创建的一个单元定义为杂交元。杂交元分为杂交应力元和杂交应变元,杂交应力元根据位移和应力变分原理进行推导,最后求解是以节点位移为未知数的有限元。Voronoi单元有限元法(voronoi cell finite element method, VCFEM)是Ghosh等[12]基于Pian[11]提出的假设应力杂交元法建立的单元格式。Guo等[13]提出了一种新的考虑界面裂纹和基体裂纹的Voronoi单元,在文献[14]的基础上新加入了裂纹裂尖附近奇异应力场,准确地刻画了裂尖周围的应力奇异,并计算出准确的裂尖应力强度因子,而且裂纹的不连续性在单元中能被准确描述,并构建反映裂纹从界面裂纹向基体扩展和裂纹的跨单元的扩展的网格重划分算法,模拟了含大量微结构和裂纹的颗粒增强复合材料的界面裂纹和基体裂纹的扩展贯穿过程[15]。徐越等[16]以扩展有限元法的仿真结果为训练数据,叶片裂纹位置和裂纹长度为输入参数,建立了裂纹尖端应力强度因子的多层反向传播人工神经网络(back propagation artificial neural network, BPANN)。

现提出一种扩展二相杂交应力有限元法,通过构建包含边界裂纹、水平中心裂纹以及倾斜裂纹的两相材料的扩展二相杂交应力有限元单元模型对界面裂纹进行断裂力学分析。通过该方法得到的数值模拟结果和传统有限元分析的数值结果进行比较,验证该方法的有效性和准确性。

1 界面裂纹尖端附近应力场

如图1所示,两种材料的杨氏模量、泊松比和剪切模量分别为Ei、υi、ui(i=1,2),界面两侧材料中各存在一点Q1、Q2。在以界面裂纹尖端为坐标原点的局部坐标系(X1O1Y1)和(X2O2Y2)下极坐标分别为(L1,θ1)和(L2,θ2)。上层材料极角θ1在[0,π]范围内沿X1轴正方向逆时针测量,极角θ2在[-π,0]范围内沿X2轴正方向顺时针测量。下层材料中极角θ1在[-π,0]范围内沿X1轴正方向顺时针测量,极角θ2在[0,π]范围内沿X2轴正方向逆时针测量。包含水平中心界面裂纹的两相材料的界面裂纹近端应力σ场可表示为

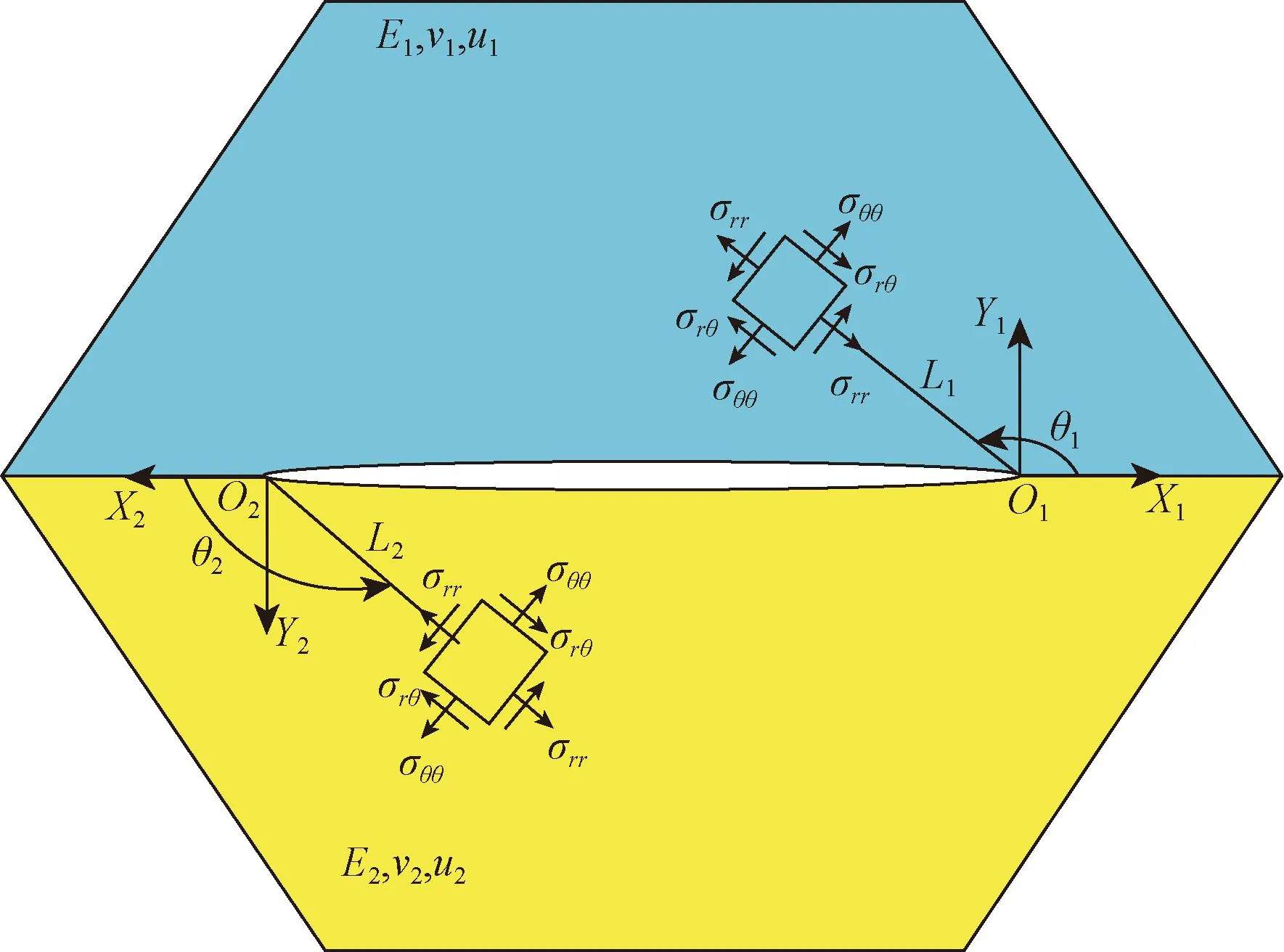
图1 裂纹尖端附近应力场Fig.1 Stress field near the crack tip

(1)

Liε=cos(εlnL)+isin(εlnL)表现出应力场的振荡奇异性;ε为振荡参数或双材料系数,其表达式为

(2)

式(2)中:βd为连接界面裂纹两侧弹性材料参数的第二个Dundur参数,第一个Dundur参数为αd。两个Dundur参数的计算公式为

(3)

式(3)中:μ1、μ2为弹性常数;k1、k2为Kolosov常数,计算式为

(4)

从式(1)、式(2)中可知,第二个Dundur参数对界面裂纹尖端应力场分布的影响较大,似乎不受第一个Dundur参数的影响。如图2所示为不同泊松

图2 不同泊松比下双材料Dundur参数βd 随弹性模量比变化曲线Fig.2 Dundur parameterβdchanges curve with elastic modulus ratio under different Poisson’s ratios

比下第二个Dundur参数随杨氏模量比的变化规律。由图2可知,当两种材料的弹性常数相同时,第二个Dundur参数βd=0。另外,从图2可以看出,βd可能取正值,也可能取负值,这取决于(Ei,υi)的匹配。当两种材料的泊松比取值相同时,βd取正数表示上层比下层软,取负数表示下层比上层软。

(5)

(6)

2 描述包含界面裂纹的两相材料的杂交应力有限元公式

以图3所示包含界面中心裂纹单元Ωe为例,其由上层材料Ω1和下层材料Ω2组成。即Ωe=Ω1∪Ω2单元外边界由四种类型:给定位移边界∂Ωr、单元

图3 包含中心界面裂纹的两相材料单元模型特征边界Fig.3 Characteristic boundary of two-phase material element model with central interfacial crack

通过最小余能原理,在满足平衡方程和边界条件情况下,余能泛函表达式为

(7)

(8)

利用Lagrange乘子将以上几种约束条件引入最小余能泛函,得到修正最小余能泛函,表达式为

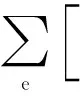
(9)

式(9)中:下标1指上层第一相材料,下标2指下层第二相材料,两相材料界面连接处变量下标为12;u为位移;n为边界外法线;σ1、σ2分别为两相材料内部平衡应力场。杂交应力单元模型中应力场的构建选取对X-THSFEM的收敛性和效率有重要影响。X-THSFEM中的应力场由三个分量组成,应力函数导出的前两部分合并起来表示为Pprβpr,界面裂纹尖端周围的奇异项表示为Picrβicr,单元内各相材料应力表达式为

(10)

(11)

单元各边界位移由相应边界段节点位移插值得到,表达式为

(12)

(13)

(14)

式(14)中:

即β=H-1Gq,

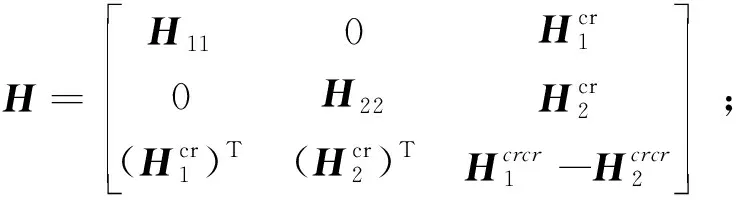
(15)

其中单元刚度矩阵表达式为

Ke=GTH-1G

(16)

3 应力函数的构造

X-THSFEM单元模型中应力场函数的构造应考虑远场应力和界面形状对应力场的影响以及裂纹尖端附近应力奇异性。图1中X-THSFEM单元模型中应力函数由3个部分组成,表达式为

Φ=Φpoly+Φrec+Φicr

(17)

式(17)中:Φpoly为Airy高阶多项应力函数刻画远场应力;Φrec为互作用应力函数描述界面的形状;Φicr为构造奇异应力场函数,描述界面裂纹尖端附近的应力集中。

3.1 多项式Airy应力函数的构造

为刻画远场应力,利用Airy应力函数构造高阶多项应力函数。Airy高阶多项应力函数在局部坐标中的表达式为

(18)

式(18)中:(xc,yc)为单元中心坐标,利用缩放系数Li=max|(xi,yi)-(xc,yc)|∕10,将全局坐标系(x,y)转变为局部坐标系(ξ,η),其中:ξ=(xi-xc)∕Li,η=(yi-yc)∕Li。由于局部坐标系与全局坐标系互相平行,故可直接得到全局坐标系下的应力分量为

(19)

3.2 互作用应力函数的构造

f(x,y)=1所在界面呈直线形状,当(x,y)→∞时,1/f(x,y)→0可以作为映射函数来构造基于界面形状的互作用应力函数,直界面中由点到线的距离公式为

(20)

基于上述映射函数,可以构造局部坐标系(ξ,η)中基于界面形状的互作用应力函数。各阶段的互作用应力函数表示为

(21)

两相材料第二部分应力分量为

(22)

3.3 界面裂纹尖端附近奇异性应力场函数的构造

以包含水平中心界面裂纹的两相材料的X-

THSFEM模型单元为例,界面裂纹长度为2a,不同各向同性材料分别位于界面上下两侧。

如图4所示,两种材料的杨氏模量、泊松比和剪切模量分别为Ei、υi、ui(i=1,2),界面两侧材料中各存在一点,在以界面裂纹尖端为坐标原点的局部坐标系(X1O1Y1)和(X2O2Y2)下,L1和L2分别为点Q1和Q2与对应裂纹尖端的径向距离。

将式(5)、式(6)代入式(1)中可得到点Q1和Q1在界面裂纹尖端1和2附近应力分量表达式为

图4 包含水平中心界面裂纹的两相材料坐标系Fig.4 Coordinate system of two-phase material with horizontal central interfacial crack

(23)

式(23)中:f1、f2、g1、g2、h1和h2为双材料系数,插值函数和坐标L、θ已知,复合应力强度因子的实部K1和虚部K2相当于第2节中提到的应力系数βicr。同时考虑两个界面裂纹尖端的影响,计算X-THSFEM中任意积分点的裂纹尖端奇异应力。由坐标变换矩阵T可以得到全局奇异应力分量为

(24)

全局应力场应充分反映远离裂纹尖端和界面的应力、界面形状对应力场的影响以及界面裂纹尖端附近的应力奇异性。因此,两相材料中的全场应力分量可以由上述3个部分叠加而成,表达式为

(25)

4 最小二乘法确定尖端应力强度因子

应力强度因子可以通过应力和位移等参数进行求解,在数值方法求解中,可以通过路径独立积分比如相互独立积分和J积分。将采用基于点的应力的最小二乘法计算应力强度因子。

如图5所示,在裂纹长度为2a的两相材料模型单元中,在裂纹尖端附近选取大量点形成半径为r的环形曲面,将点的坐标及全局应力代入式(23)中得到线性方程

σ=A+K

(26)

式(26)中:σ包含式(10)、式(11)两个部分;A包含与每个相点坐标有关的插值函数;界面裂纹应力强度因子K可以通过式(26)两边乘以A-1得到。

图5 用于计算应力强度因子的域Fig.5 Fields used to calculate SIF

5 数值算例

通过X-THSFEM单元模型数值模拟结果与商用计算软件ABAQUS的有限元结果或已有文献结果进行比较加以验证X-THSFEM的有效性和准确性。

算例1以包含水平边界裂纹的双材料矩形板为例。

如图6所示,包含水平边界裂纹的双材料矩形板长3L=15 mm,宽度L=5 mm,边界裂纹长度a=1 mm,上下层材料的杨氏模量和泊松比分别为E1=4.8×104MPa,E2=480 MPa,υ1=υ2=0.3,板材上下边界施加1 MPa的拉伸载荷。相同几何形态下,通过对X-THSFEM单元模型的分析和ABAQUS软件所得到结果进行比较,如图7所示为应力分量σx、σy、σxy云图。

为比较包含边界裂纹的两相材料在E1/E2不同的情况下,无量纲应力强度因子的取值变化情况,如表1所示。从表1可知,X-THSFEM得到的裂纹尖端附近的无量纲SIF将与Gu等[17]给出的边界元方法计算的参考结果和Jiang等[18]基于广义有限差分法计算的参考结果非常接近。进一步说明本文所提方法的准确性。

算例2以包含水平中心界面裂纹的双材料矩形板为例。

如图8所示,板长2L=10 mm,宽度L=5 mm,中心界面裂纹长度a=2 mm,上下层材料的杨氏模量和泊松比分别为E1=4.8×104MPa,E2=480 MPa,υ1=υ2=0.3板材上下边界施加1 MPa的拉伸载荷P。在相同几何形态下,通过如图9所示X-THSFEM模型与ABAQUS软件所得到的水平应力分量σx云图和垂直应力分量σy云图,可以观察到,X-THSFEM模型得到的这些应力云图与ABAQUS软件得到的应力云图中应力分布趋于一致。

当E1/E2=100时,为保证应力强度因子的收敛性,如表3所示通过对应力系数的个数(多项式应力函数的项数M和互作用应力函数的项数N)不同取值,应力强度因子K1的变化。

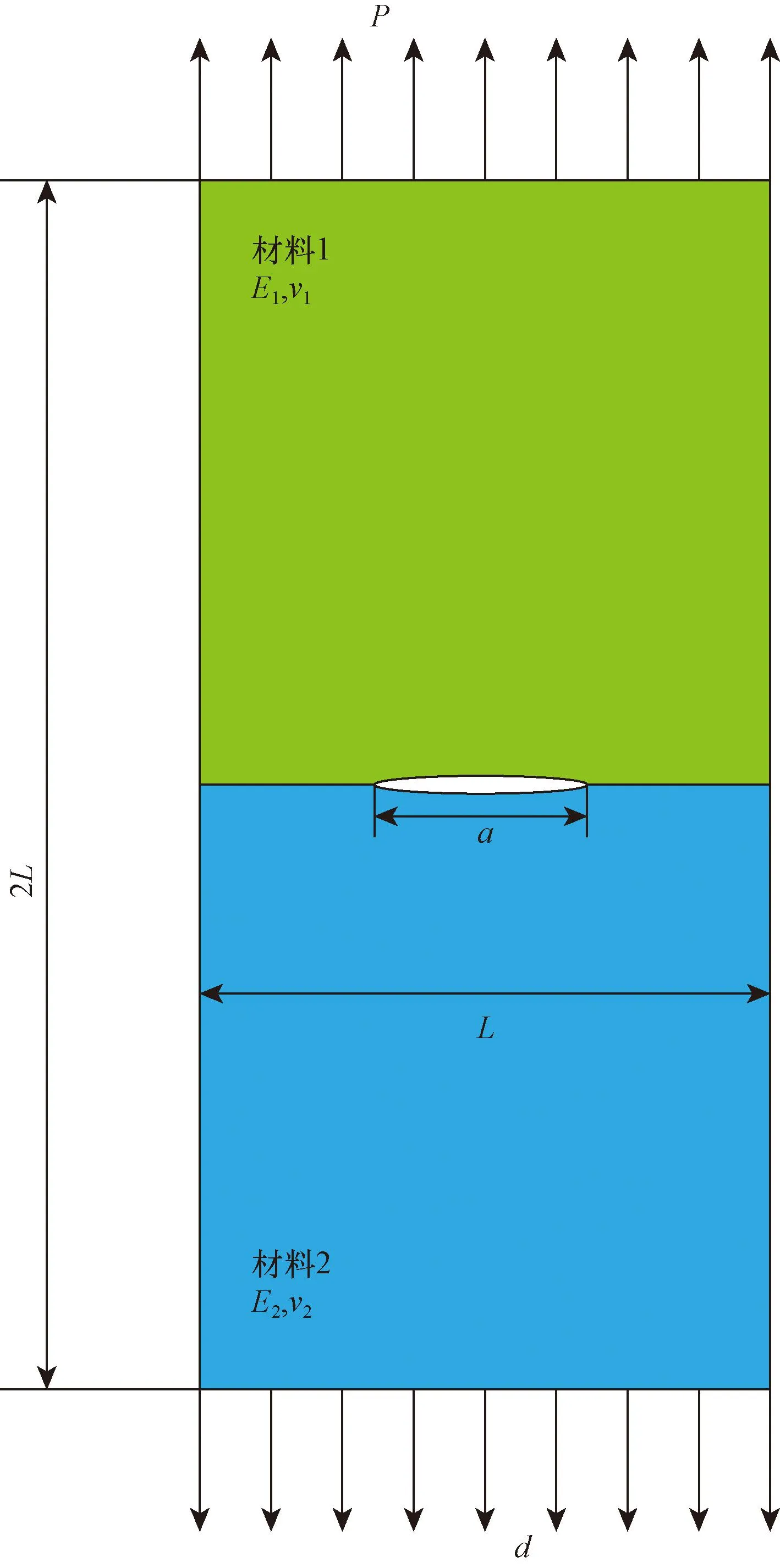
图8 包含水平中心界面裂纹的双材料矩形板Fig.8 A double-material rectangular plate with a horizontal central interface crack

图9 包含水平中心裂纹的双材料矩形板X-THSFEM 模型和ABAQUS模型应力云图Fig.9 X-THSFEM model and ABAQUS model of bi-material rectangular plate with horizontal central crack stress nephogram

表2 包含边界裂纹的两相材料无量纲应力强度因子Table 2 Dimensionless stress intensity factors for two-phase materials containing boundary cracks

如表3所示,当多项式应力函数的项数M=117时,互作用应力函数的项数N取7～25,应力强度因子K1保持不变,为保证应力强度因子的收敛性,最终可确定M=117,N=18。

当裂纹面与水平方向呈一定倾斜角度时,如图10所示,其中L=5 mm,裂纹面倾斜角度为θ。上层材料的杨氏模量和泊松比分别为E1=4.8×104MPa,υ1=0.3;下层材料杨氏模量和泊松比分别为:E2=480 MPa,υ2=0.3,板材上下边界施加1 MPa的拉伸载荷。

为证明本文方法的准确性,如图11所示,当裂纹倾斜角度θ分别为15、30、45、60时,通过对X-THSFEM模型与ABAQUS软件得到的水平应力分量包含不同倾斜角度界面裂纹的两相材料在E1/E2不同的情况下,无量纲应力强度因子的取值变化情况,如表4所示,X-THSFEM得到的裂纹尖端附近的无量纲SIF与ABAQUS软件得到的无量纲SIF趋于一致,进一步说明本文所提方法的准确性。

表3 应力系数不同的情况下应力强度因子取值Table 3 Values of SIF under different stress coefficients

图10 包含倾斜界面裂纹的双材料矩形板Fig.10 Bimaterial rectangular plate with inclined interface crack

σx云图和垂直应力分量σy云图进行比较,从图11中可以观察到,X-THSFEM模型得到的应力云图与ABAQUS软件得到的应力云图中应力分布趋于一致。

算例3包含多个界面裂纹的层合板。

如图12所示,对于由多种各向同性材料组成,包含不同类型界面裂纹的层合板,通过构建包含多个单元的扩展二相杂交应力有限元模型对界面裂纹进行断裂力学分析,其中每个二相杂交应力单元包含边界裂纹、中心界面裂纹以及同时包含中心界面裂纹和边界裂纹。构建的扩展二相杂交应力有限元模型包含9个单元。

如图13所示,每层材料弹性模量及泊松比:E1=E4=730 GPa,E2=E3=73 GPa,E5=E6=7.3 GPa,υ1=υ2=υ3=υ4=υ5=υ6=0.2。第1号单元两侧同时包含边界裂纹,第2、3、5、7、8号单元只一侧包含边界裂纹,第4、9号单元包含水平中心裂纹,第6号单元包含水平中心裂纹以及两侧同时包含边界裂纹。通过对包含多个单元的扩展二相杂交应力有限元模型进行分析得到应力分量σx、σy、σxy云图,如图14所示。为进一步说明X-THSFEM对于分析多种材料组成,包含不同类型界面裂纹的层合板具有很大优势,如表5所示,研究裂纹尖端SIFs随弹性模量比值的变化趋势,选取两组上下两层材料弹性模量不同比值的有限元模型,当随着单元内上下层材料弹性模量之比的增大,K1相应增大,K2的绝对值也相应增大。

表4 包含不同倾斜角度界面裂纹的两相材料 无量纲应力强度因子Table 4 Dimensionless stress intensity factors for two-phase materials with interfacial cracks at different inclined angles

图11 包含倾斜界面裂纹的双材料矩形板X-THSFEM模型和ABAQUS模型的应力分量云图Fig.11 Stress component nebulae of double-material rectangular plates with inclined interface crack of X-THSFEM model and ABAQUS model

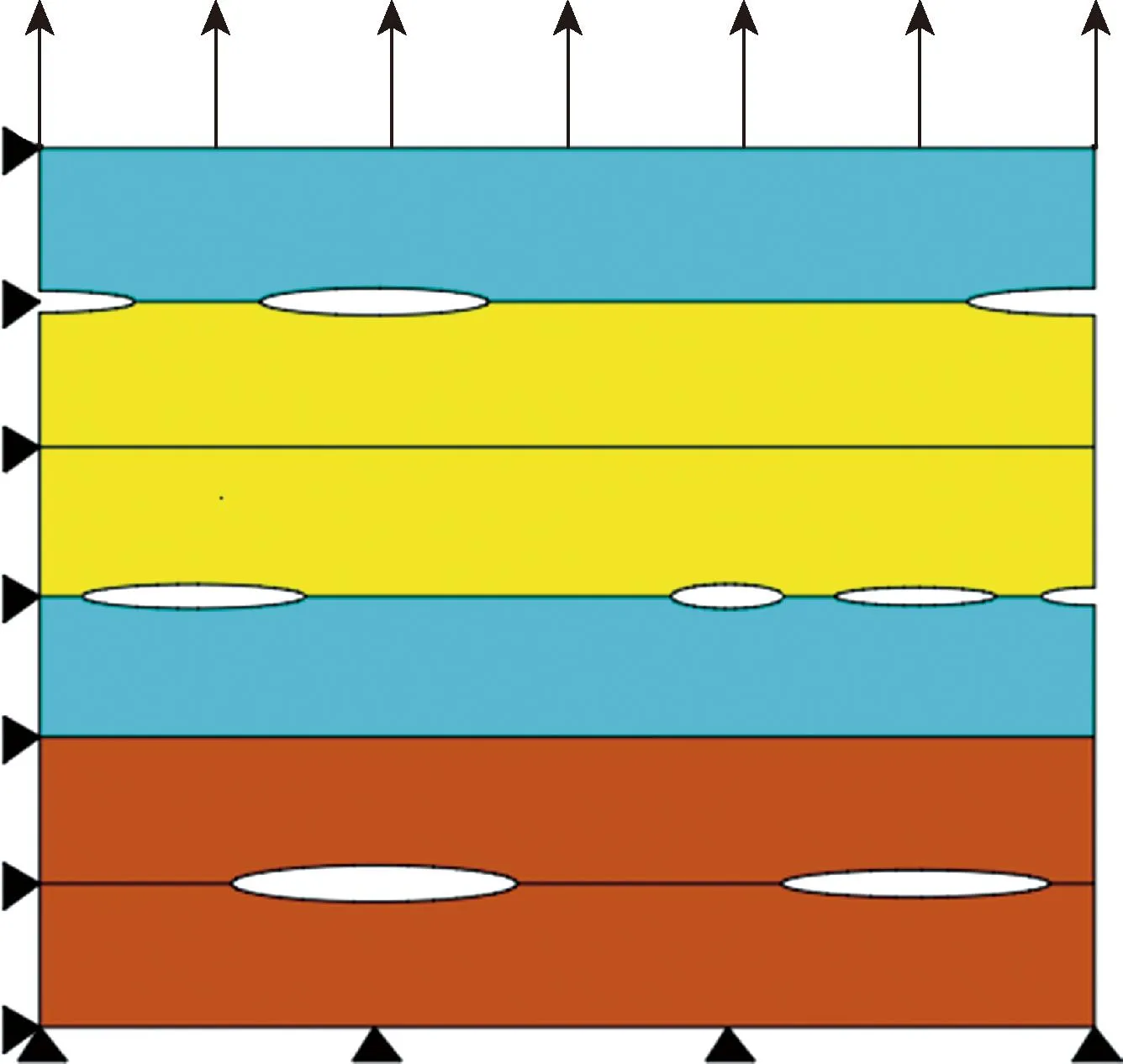
图12 包含不同种界面裂纹的多相材料矩形板Fig.12 Rectangular plate of polyphase material containing different kinds of interfacial cracks

图13 扩展二相杂交应力有限元模型Fig.13 Extended two-phase hybrid stress finite element model

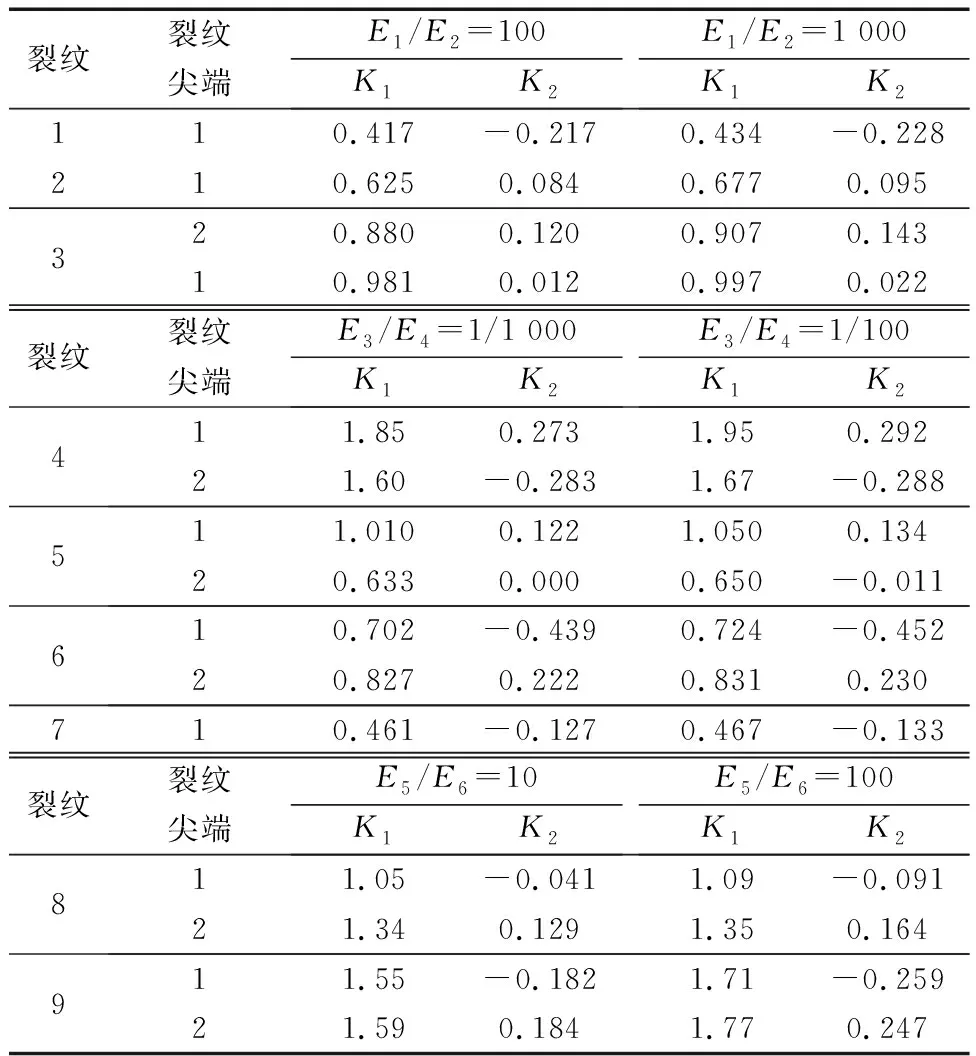
表5 弹性模量不同比值时界面裂纹应力强度因子Table 5 Stress intensity factors of interfacial crack with different ratio of elastic modulus

6 结论

提出了一种扩展二相杂交应力有限元法,通过构建包含边界裂纹、水平中心裂纹以及倾斜裂纹的两相材料的扩展二相杂交应力有限元单元模型对界面裂纹进行断裂力学分析。应用Lagrange乘子法将各个界面裂纹面面力为零边界条件和未断裂界面的面力连续条件引入修正余能泛函中,在每一相材料域内假设高阶多项式应力函数,充分考虑界面形状的影响,构建互作用应力函数,引入双材料界面裂纹裂尖附近奇异应力场函数。基于Fortran程序求解后得到单元应力场,采用最小二乘法计算了界面裂纹的应力强度因子。通过该方法得到的数值模拟结果和商业有限元软件ABAQUS模拟结果进行比较,结果趋于一致,进而对由不同种各向同性材料组成,包含多种界面裂纹的层合板进行分析,说明该方法的有效性和准确性。为后期对界面裂纹的扩展研究提供理论和方案基础。