基于麻雀搜索算法优化支持向量回归的装配式建筑施工安全投入优化
2024-01-02常春光凌霄雪
常春光, 凌霄雪
(1.沈阳建筑大学管理学院, 沈阳 110168; 2.沈阳建筑大学城市发展研究院, 沈阳 110168)
装配式建筑作为建筑业转型发展的必然趋势,正在逐步扩大其市场占有率,据住建部统计,2020年中国新开工装配式建筑面积在全国新建建筑面积中占比高达20.5%。但因其施工特点明显区别于传统建筑,如施工现场作业工种结构改变、重型塔吊作业频繁、不同工种工人需在同一工作面交叉作业等,为装配式建筑施工现场安全管理带来新的挑战。施工安全状态与安全投入密切相关,针对安全资源投入,已有学者进行了大量研究,Smith等[1]对安全投入与事故发生率的相关性进行了研究论证,认为安全投入可有效降低事故发生率与死亡率,保障企业生产经营活动的顺利开展。姜福川等[2]通过熵权-TOPSIS(technique for order preference by similarity to an ideal solution)法构建煤矿生产安全投入方案评价模型,证明合理的安全投入结构可以实现以最小投入实现最大安全效益的目标。何正豪等[3]将安全生产措施费投入列入项目安全的主要风险因素。王晓燕[4]通过基于关联规则精准挖掘煤矿安全数据,根据数据挖掘结果,构建煤矿安全投入决策模型,获取最优决策方案。杨玉梅等[5]借用支持向量分别构建了适用于煤矿及航运行业的安全投入优化模型,并证明模型具有科学性。在麻雀搜索算法(sparrow search algorithm, SSA)方面,马小晶等[6]将Circle混沌映射机制引入到麻雀优化算法中。邓立霞等[7]利用混沌映射进行种群初始化。陈超泉等[8]研究了麻雀搜索算法与海鸥优化算法的融合机制。在支持向量回归(support vector regression, SVR)方面,近年研究热点主要集中在其他算法与SVR的融合机制方面,张金水等[9]将极限梯度爬升算法与支持向量回归算法结合应用。邹宗民等[10]将粒子群优化算法与支持向量回归结合应用到高速公路短时交通流预测中。王鑫等[11]研究了麻雀搜索算法优化支持向量机的融合机制。上述专家学者的研究成果丰富了安全投入、SSA和SVR领域的理论与方法。但有关工程建设领域的施工安全投入的研究,特别是面向装配式建筑施工安全投入的研究更为缺乏。目前,装配式建筑施工安全管理问题的研究多聚焦于安全风险评价及风险因素识别等方面。
在此背景下,现借鉴其他领域较为成熟的安全投入优化研究方法,结合装配式建筑施工安全管理实际情况,构建基于麻雀搜索算法的支持向量回归模型,对施工安全投入与安全事故经济损失间的定量关系进行拟合,建立安全投入优化模型,并通过案例分析,验证模型的可行性。
1 施工安全投入优化模型的构建
1.1 问题描述
建筑业作为一种高危行业,事故隐患始终伴随着工程施工全过程,为保障建筑施工安全、降低人员伤亡率,企业需进行必要的安全投入。建筑工程安全投入分为主动性(保证性) 安全投入与被动性(损失性) 安全投入[12]。前者是指为避免事故发生,而在安全教育、设施设备、劳动保护、文明施工及管理等方面进行的预防性安全投入;后者是指事故发生后为处理安全事故或人员伤亡而支付的损失性安全投入。在建筑施工过程中,除安全投入金额之外,安全投入分配结构也与安全事故发生概率密切相关。安全投入与事故损失间存在非线性关系,在安全投入份额一定的情况下,如何通过安全投入最优化分配使安全事故损失最小,成为建筑施工安全投入优化急需解决的问题。相比于常见的柯布-道格拉斯(Cobb-Donglas,C-D)生产函数等拟合方法,SVR在解决非线性、小样本和高维度问题时具有更好的预测能力[13-14]。
1.2 安全投入与事故损失关系函数拟合
以装配式建筑施工安全投入为输入值,安全事故损失为输出值,利用SVR拟合二者间定量关系,进而得到优化模型的目标函数。
SVR模型通过映射函数φ(X)实现训练集D={(X1,Y1),(X2,Y2),…,(Xm,Ym)} (Xi∈Rn,Yi∈R)向高维特征空间F映射[15],其中,X泛指映射函数的自变量,Xi与Yi分别表示训练集中的第i个训练样本的输入向量值与输出值。进而确定线性模型为
f(Xi)=[wTφ(Xi)]+b
(1)
式(1)中:w为权重向量;b为常数项。
SVR的本质是在空间内找到一个最优回归超平面,满足距离该平面最远的样本点间隔最小。并假设回归函数f(Xi)与实际值Yi之间存在可容许最大误差为ε,仅当f(Xi)与Yi之差的绝对值大于ε时才计算损失,最大误差边界线穿过的数据样本即为支持向量。
于是支持向量回归问题写为
(2)
(3)
式中:σ为惩罚因子;lε为ε的损失函数;|u|=|f(Xi)-Yi|。
实际应用中,很难确定适合的ε,故引入松弛变量ξ、ξ*,分别表示回归函数f(Xi)与实际值Yi之间可容许最大正向误差、最大负向误差的松弛变量,放松函数对间隔的要求,从而得到
(4)
s.t. [wTφ(Xi)+b]-Yi≤ε+ξi
(5)
(6)
ξi≥0,ξi*≥0,i=1,2,…,m
(7)
引入拉格朗日乘子α,得到式(4)~式(7)的对偶问题为

(8)
(9)
(10)

(11)
核函数的选择直接影响SVR模型的精准度,参考文献[16-17],选取径向基函数作为本文所用模型的核函数,即
K(Xi,X)=exp(-g‖Xi-X‖2)
(12)
式(12)中:Xi为训练集的输入向量;X为预测集的输入向量;g为核函数参数,通过模型训练得到。
得到SVR模型的决策函数后,便可用函数f(X)代表施工安全投入与安全损失之间的定量关系,为达到在总安全投入费用固定的前提下安全事故经济损失最小的优化目标,将装配式建筑施工安全投入优化模型的目标函数表达为
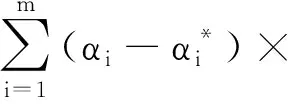
(13)
1.3 优化模型建立
装配式建筑施工过程中存在大量的吊装及高空作业环节,施工工艺也有本质上的变化,为装配式建筑施工带来更多风险因素,具体包括操作人员技术水平、操作人员的安全意识、施工机械的安全状态、施工现场环境状况等[18]。将用于控制安全风险的d个安全投入分项作为模型输入指标,对模型约束条件分析如下。
由于受到项目规模、总成本等约束,安全投入总额不会无限增加,同时,受到行业制度的规范,安全资源的总投入必须满足最小投入要求,则有
(14)
式(14)中:rmin为安全投入占工程建安费的最小比重;rmax为公司能够承受的安全投入比重最大值;xv为第v个输入指标;C为项目建筑安装工程造价。
安全投入指标对施工安全水平的作用方式各不相同,忽视任何一项都可能引发安全事故,因此,每项指标都需要一个最小投入比rv作为保障,即
(15)
部分安全投入指标之间存在相互作用、相互替代关系,导致某一安全投入效果受其他几项指标的共同影响,若这几项指标投入额过低可能会削弱原有投入效果。因此,需要设定投入下限来约束这几项安全指标的投入情况,即
(16)
式(16)中:rs表示某几项需要重点考虑的安全投入指标的最小投入比;Ω表示某几项需要重点考虑的安全投入指标的序号组成的集合。
综上,装配式建筑施工安全投入优化模型表达式为

(17)
(18)
(19)
(20)
2 模型参数优化
借助SVR可以提高安全投入与安全事故损失的定量关系拟合精度,但同时也使模型更加复杂。SVR的拟合效果在很大程度上取决于参数的选择,为避免寻优速度慢、容易陷入局部最优等问题,本文选用麻雀搜索算法进行模型参数寻优。
2.1 SSA算法
SSA算法提出于2020年[19-20],相比传统算法,该算法结构简单、易于实现,且收敛能力较强,在避免局部最优方面表现也更为出色[21-22]。受到麻雀觅食行为启发,SSA在寻优过程中将个体分为3种角色(发现者、跟随者和警戒者)用以更高效地找到最优结果。
假设群体中有n只麻雀,则麻雀种群可表示为
(21)
式(21)中:d为待优化问题的维度,即输入指标的数量;f为适应度值,所有麻雀的适应度值可表示为
(22)
在算法中,发现者负责找到食物最丰富的区域,且适应度值越高的发现者越容易获取食物,当觅食区域安全值低于危险值时,发现者会带领雀群飞至其他区域进行觅食。据此,将发现者的位置迭代过程描述为
(23)
式(23)中:t为当前迭代数;Xi,j为个体i的位置信息,j=1,2,…,d;a为(0,1]上随机数;Nmax为迭代次数上限;R2为报警值;S为安全值;Q为服从正态分布的随机数;L为所有元素为1的1×d矩阵。当R2 跟随者通过监控发现者获得食物,且二者身份可相互转化,当跟随者的适应度值过低,难以满足需求时,会飞至其他地方继续觅食。据此,跟随者的位置更新表示为 (24) 式(24)中:XP表示当前发现者所处的最优位置;Xworst表示当前全域最差的觅食位置;A表示元素被随机赋值为1或-1的1×d的矩阵;A+表示伪逆矩阵,且A+=AT(AAT)-1。当i>n/2时,表示第i个跟随者的适应度值较低,无法与发现者争夺食物,需要更换觅食区域;当i≤n/2时,表示第i个跟随者将在最优发现者XP附近觅食。 遇到危险时发出鸣叫示意的麻雀称为警戒者,其位置更新表示为 (25) (1)算法参数初始化。 (2)计算初始适应度值。 (3)根据式(23)~式(25)更新发现者、跟随者和警戒者的位置。 (4)计算当前适应度值并更新个体位置。 (5)满足终止条件后输出模型参数最优值,否则返回步骤(3)。 (6)将寻优结果代入SVR模型。 3.1.1 数据样本的获取 考虑到装配式建筑施工技术于近几年内才逐渐趋于成熟,且建筑工程之间建设投入及损失情况大同小异,故本文选取近5年内不同的20个装配式建设项目,对工程安全投入及安全损失情况进行分析。结合装配式建筑施工实际情况,针对施工现场相关安全投入子项重新进行分类和说明,最终确定五项安全投入分项作为本次模型输入指标,具体指标及指标内涵说明如表1所示。 将20个装配式建设项目的安全投入情况按上述指标重新分配后,得到原始数据样本,如表2所示,以此为依据对SSA-SVR模型进行拟合训练及检验。 表1 安全投入指标及内涵介绍Table 1 Introduction to the connotation of safety investment indicators 3.1.2 原始数据预处理 为得到更好的模型训练效果,本文选用mapminmax函数对原始数据按行进行归一化处理,将原始数据映射到区间[0,1]上,函数表达式为 (26) 3.1.3 模型的参数初始化设置 在麻雀搜索算法中将搜索的迭代次数设为200;种群数量设为30,其中70%为发现者,20%为警戒者,其余10%为跟随者;安全阈值设为0.6;惩罚因子σ和核函数参数g的初始范围分别设置为[0.001,100]、[0.001,1 000]。 表2 施工安全投入及事故经济损失原始数据Table 2 The original data of construction safety investment and accident economic loss 3.1.4 模型训练与拟合结果检验 采用5折交叉验证法对SSA-SVR模型进行测试和验证,以达到在有限数据样本中获得更多有效信息的目的,弱化小样本数据的缺陷。 借助MATLAB软件对SSA-SVR模型代码运行后,得到种群适应度函数曲线如图1所示。 利用SSA算法进行SVR模型参数搜索后,得到最优参数为σ=98.168 7,g=4.097 8,均方误差MSE= 0.547 27。 将最优参数σ和g的代带回SVR模型,对样本数据中的训练集进行预测训练,得到期望值与预测值的拟合曲线,如图2所示。将余下5组样本数据作为测试集代入训练好的SSA-SVR模型,验证模型预测的精度,得到期望值与预测值的拟合曲线,如图3所示。 图1 种群适应度函数曲线Fig.1 Population fitness function curve 图2 训练集期望值与预测值的拟合曲线Fig.2 The fitted curve of the expected and predicted values of the training set 图3 测试集期望值与预测值的拟合曲线Fig.3 The fitted curve of the expected and predicted values of the test set 模型对所有样本预测结果的均方误差MSE约为0.547,相关系数约为0.96,有较好的拟合效果。 模型训练测试结果表明,上述构建的SSA-SVR模型能够很好地拟合装配式建设项目施工过程中安全投入与事故经济损失之间的量化关系。 经过训练和检验后,在原数据样本中得到13个支持向量作为模型的支撑数据,即 (27) 将模型求得的最优参数及支持向量相关数据代入式(17),得到优化问题的目标函数为 (28) 选取华润H装配式住宅建设项目为实证对象,检验上述模型的可行性和有效性。该项目建安工程造价为53 086万元,作为当地装配式建筑试点项目,本项目决定最高可提取建安工程费的3%作为施工安全投入,以保障项目的安全开展,即rmax=0.3。同时,根据安全生产费提取规定:房屋建筑工程安全费用提取不得低于建安工程造价的2.5%,故rmin=0.25。 考虑到装配式建设项目施工现场安全管理要求及项目本身对安全决策的限制,对各安全投入分项及对安全状态影响较大的安全投入指标组合设定投入下限,构建安全投入优化模型,即 (29) (30) (31) (32) (33) (34) (35) (36) (37) 式(30)表示安全投入总额的上下限;式(31)~式(36)表示各安全投入分项的下限;式(37)表示在装配式建筑施工现场人员与施工设施作为关键因素,在相关安全投入上必须达到的投入要求。 经过编程计算,得到H装配式建设项目事故经济损失最小值约为594.56万元,此时安全投入最优组合为X=[460.79, 148.64, 312.15, 133.78, 431.06],总安全投入费用约为1 486.41万元。安全投入优化模型求得的结果与项目原安全投入数据对比情况如表3所示。 通过对比可知,经安全投入优化模型重新分配后,H项目安全事故经济损失降低90.24万元,安全投入总额减少约106万元。此外,原项目在文明施工和劳动保护两个分项的投入分别达到50万元和80万元以上的投入差额,造成了资金的浪费,而在安全教育及安全设施分项上的安全投入略有不足。说明管理者在进行安全投入决策时缺乏科学依据,应调整资源投入分配比重以达到节约成本、降低事故发生概率的目的。 表3 安全投入及事故经济损失数据对比Table 3 Comparison of safety investment and accident economic loss data (1)通过SSA-SVR模型拟合训练,得到装配式建筑施工安全投入与事故经济损失的定量关系函数,构建安全投入优化模型。 (2)基于SSA-SVR的安全投入优化模型能有效地节约安全投入成本,降低事故经济损失,为施工安全投入决策提供理论支撑。 (3)由于受到样本数量及实际工程安全投入财务数据的限制,模型参数寻优结构受到随机影响。可通过增加样本数量提高模型预测精度。2.2 SSA算法优化参数流程
3 模型验证与案例分析
3.1 SSA-SVR模型训练与检验

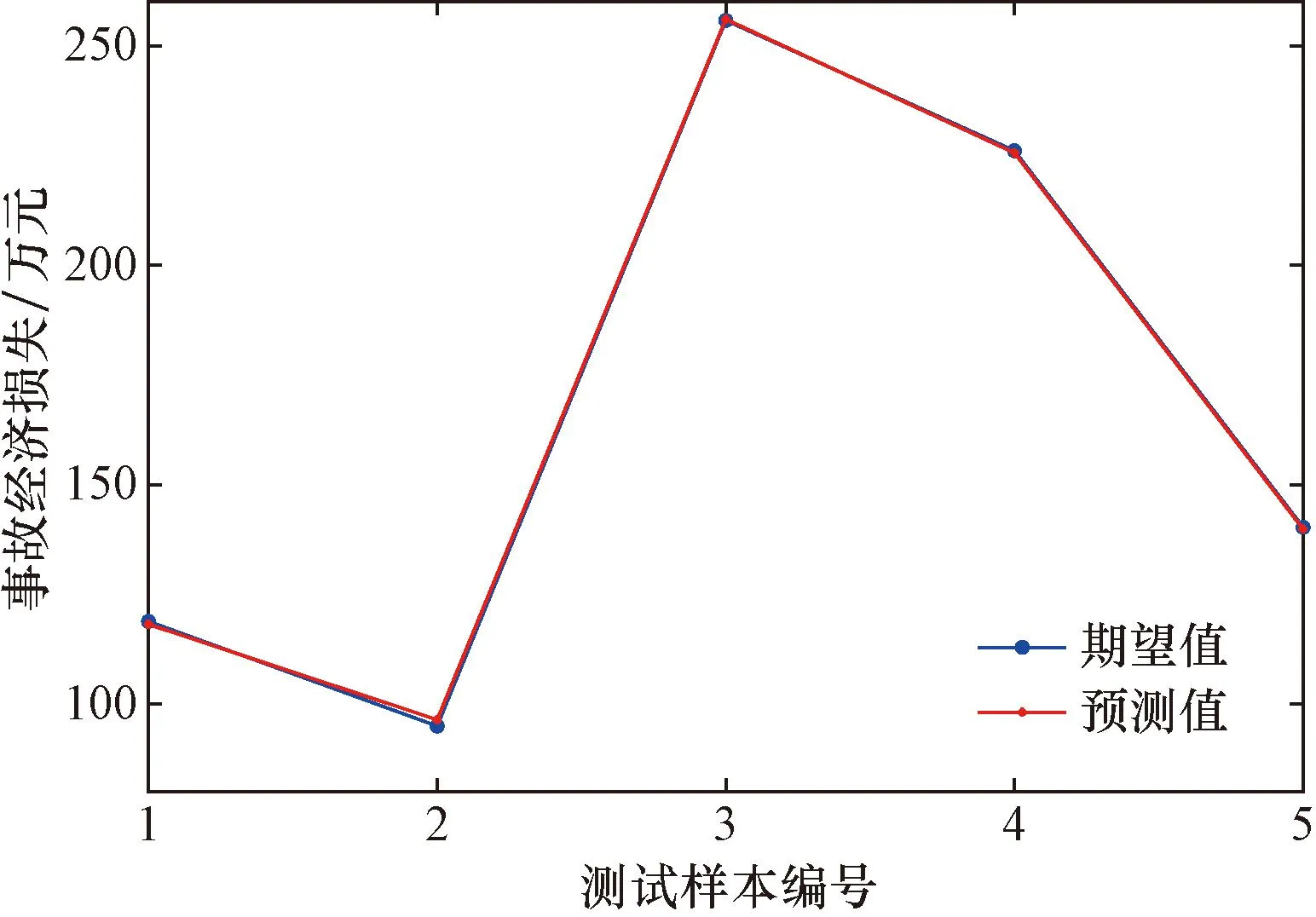
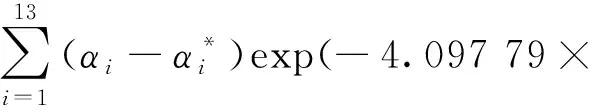
3.2 实例分析

4 结论
