破碎岩石颗粒形态特征量化描述体系

2024-01-02李雪晴李国栋

科学技术与工程 2023年35期

李雪晴, 李国栋*

(1.河北工程大学矿业与测绘工程学院, 邯郸 056038; 2. 河北省煤炭矿井建设工程技术创新中心, 邯郸 056038; 3. 邯郸市深部巷道围岩控制及灾害防治重点实验室, 邯郸 056038)

破碎岩石材料具有压实性强、透水性好、价格低廉、取材方便等优势,作为主要的充填和支护材料,目前已被广泛应用于道路桥梁建设、矿山和水利工程回填等领域[1]。破碎岩石的力学性能是决定工程设计的重要依据。岩石颗粒的粒径、表面粗糙度、长径比等形态特征不仅影响颗粒组的堆积密度,还决定了颗粒间的相对错动、咬合结构、力链传递等细观力学行为。一般而言,当岩石颗粒形状规则性较差、棱角较多时,颗粒间空隙相对增多、接触面积减小,且受载时颗粒易形成咬合结构,棱角处应力集中明显,易变形破坏。随着加载的进行,以上细观力学行为又将进一步影响破碎岩石颗粒组的宏观承载和破坏特征。

针对岩石颗粒细观形态特征对宏观力学响应的影响研究,国内外学者获得了较多成果。崔景昆等[2]针对不同粒径的矸石以及不同配比的矸石粉煤灰进行压实试验,发现充填体的抗变形能力与粒径相关,粒径取0～30 mm时最强。吴东涛[3]对矸石进行单一级配压实试验,发现矸石粒径影响压实特性,小颗粒矸石形成“光滑-光滑-光滑”作用机制;大颗粒矸石形成“光滑-震荡-光滑”作用机制。龚健等[4]用离散元模拟方法,发现相对密实度峰值强度和残余强度受颗粒表面光滑度影响较大。Cho等[5]采用球形度、圆形度和平滑度评估土壤颗粒的形态特征,发现颗粒不规则性增加会导致刚度降低。王蕴嘉等[6]建立了不同球度的颗粒模型并进行了数值模拟试验,发现颗粒圆度较高且级配均匀时,球度对峰值摩擦角影响较小。邹德高等[7]、郭禹希等[8]、周光军等[9]发现岩石颗粒破碎率随平均球度的增加而减小,极限轴向应变随粒径增大而增大,岩石颗粒组的宏观应变随颗粒长宽比增加而增加。

在早期针对岩石颗粒力学行为的研究中,采用筛分法获得的颗粒粒径是最主要的描述参数。随着图像处理、三维扫描、CT(computed tomography)扫描等技术的发展,岩石颗粒形态特征的描述逐渐趋于多元化和全面化。李瑞泽等[10]对碎石颗粒进行了三维点云采集,统计分析了延伸率、扁平度、球度等形状参数。章涵等[11]基于CT技术与球谐级数提出了三维颗粒形态构建新方法。韩照等[12]采用CT扫描技术建立了含球形度、凸率、粗糙度、比表面积的形貌公式。李皋等[13]使用三维激光扫描技术获取砾石颗粒形态并开展了物理试验,发现粒径对砾岩的破坏机理和形式影响不明显。陆瑞等[14]引入主曲率均值平方根(root mean square,RMS),构建了颗粒多尺度形态特征指标体系。Krumbein[15]提出颗粒长、中、短直径快速视觉法测量颗粒圆度。蒋丽滢等[16]引入了定量体视学法获得的试样级配与颗粒圆度共同表达颗粒的外部形貌。胡建强等[17]采用傅里叶级数表述颗粒形状、棱角度和表面纹理。Al Rousan[18]、Chandan 等[19]、Vallejo[20]、Zhao 等[21]将小波分析、分形学、傅里叶级数等引入颗粒定量描述中。聂志红等[22]采用分形维数和正态分布检验方法确定了随粒径减小,颗粒长扁度和粗糙度逐渐减小,棱角度、球度和分形维数逐渐增大。

采用图像处理方法对岩石颗粒进行描述和定量分析已成为颗粒形态特征研究的主要方法。但目前,现有的研究多为针对单一形状因子描述,并未形成认同性高的描述体系。基于现有研究中存在的不足,针对破碎岩石颗粒二维形态特征的量化描述开展研究,通过图像分析获取岩石颗粒的形态数据,采用多元回归分析对各形态参数的影响效果进行评价,最终建立岩石颗粒量化描述体系。

1 破碎岩石颗粒二维形态特征分析

1.1 岩石颗粒形态特征描述

岩石颗粒形态特征的量化描述多是基于形状参数,王步雪岩等[23]以面积A、周长P、凸面积CA、凸面积周长CP、长度L、等面积圆直径DA、等周长圆直径DP等颗粒基本尺寸为基础[23],构建密实度S0、圆度R0、球形度Sp、凸度C0等颗粒形状参数,表达式为

S0=A/CA

(1)

R0=4A/(πL2)

(2)

Sp=DA/DP

(3)

C0=CP/P

(4)

刘清秉等[24]以颗粒等效直径D、周长P、长度L、宽度B、内切圆半径Ri、外接圆半径Rc、外接多边形周长Pc等几何数据为基础,构建整体轮廓系数α、扁平度e、球形度S、棱角度Ag、粗糙度γ等颗粒形状参数,表达式为

α=πD/P

(5)

e=L/B

(6)

S=Ri/Rc

(7)

Ag=Pc/P

(8)

γ=(P/Pc)2

(9)

韩照等[12]以体积V、表面积S、半径R、像素点等基础几何数据构成的球形度Sp、凸率Cr、表面粗糙度Ra、表观密度ρa等形状参数的试验研究变化规律的基础上,又将形状参数与粒径拟合,获得三维岩石颗粒形貌参数Ss函数式,反映4个维度形貌参数与表观密度、粒径相互影响的规律。形貌参数函数式为

Ss=-278.724 7Sp+156.984 7Cr+ 11.873 5[Ra/(ρad)]+75.911 2

(10)

综上所述,颗粒形态特征研究一般是以几何参数为基础构建形状参数,直接对比形状参数或者建立描述体系,必要时进行试验验证。颗粒宏观形状多采用轴向尺寸进行量化[14],如最大径长度与最小径长度。基于此,本研究确定的基础几何参数如表1、图1所示。

以基础几何参数构建球形度(sphericity)、圆形度(circularity)、矩形度(rectangularity)3个形状参数,确定CSR形貌特征描述体系,对碎石颗粒形态进行量化分析。

球形度[25]反映颗粒的狭长程度,计算公式为

(11)

圆的球形度为1,其他形状的球形度取值范围为[0,1),下面以规则几何图形代表不同岩石颗粒a、b解释说明,直观对比如图2所示。两颗粒最小半径相等,最大半径越长,球形度越小,颗粒越狭长。

表1 破碎岩石颗粒基础几何参数定义Table 1 Definition of basic geometric parameters of rock fragments

图1 破碎岩石颗粒基础几何参数表征Fig.1 Characterization of basic geometric parameters of rock fragments

圆形度[25]反映物体接近圆形的程度,也称区域的紧凑性,计算公式为

(12)

颗粒圆形度直观对比如图3所示,在等直径外接圆条件下,颗粒c的区域紧凑性更强,故圆形度越大,颗粒越接近圆形,越规则。

矩形度[25]反映了物体在最小外接矩形中的填充程度,计算公式为

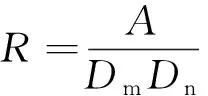
(13)

颗粒矩形度直观对比如图4所示,矩形的矩形度大于圆形大于不规则图形,在一定程度上表征颗粒的规则性。

图2 颗粒球形度对比表征Fig.2 Comparative characterization of fragments sphericity

图3 颗粒圆形度对比表征Fig.3 Comparative characterization of fragments circularity

图4 颗粒矩形度对比表征Fig.4 Comparative characterization of fragments rectangularity

1.2 CSR形貌特征描述方法

在矿用充填矸石中随机选取100块破碎岩石颗粒,岩石颗粒多为石英岩。在提取图像时,将岩石颗粒稳定放置,固定相机位置,拍摄其俯视图,期间保证光线充足不产生过暗阴影对后续图像处理造成影响。为准确识别颗粒几何轮廓线获取数据,将碎石颗粒投影图像进行二值化处理,如图5所示。

将提取的二值化图像导入Image-pro plus,定标绘制破碎岩石颗粒的二维轮廓曲线,识别获取岩石颗粒的基础几何数据,包括最大中心半径、最小中心半径、周长、面积、最小径长度、最大径长度。基于基础几何数据得到样本的形状参数包括球形度S、圆形度C和矩形度R。结果显示,所选碎石的粒径分布范围为(8.42 mm, 72.83 mm),矩形度分布范围为(0.61, 0.79),圆形度分布范围为(0.63,0.94),球形度分布范围为(0.28,0.81)。

图5 碎石颗粒二值化处理Fig.5 Binary processing of rock fragments

1.3 单一颗粒不同投影描述结果

选取两岩石颗粒,获取其俯视、正视、侧视方向的二维图像处理后进行分析,如图6所示。

图像经Image pro plus软件识别获取基础几何数据,数据处理后得到的形状参数如表2所示。

结果显示,示例中的两颗粒矩形度相差不大,在其最小外接矩形的填充程度相似,矩形度描述下的规则程度相似;圆形度与球形度均为颗粒e小于颗粒f,相差较大;根据两参数定义可知,球形度描述下颗粒e更为狭长,圆形度描述下颗粒f规则程度更大。综上所述,作为独立存在的形状参数,可以单一量化对比分析。但仅考虑单一因素比较片面,描述的准确性也有待考量。当三个参数同时考虑时该以何标准描述是接下来需要研究的问题。

图6 颗粒三视图示例Fig.6 Examples of three views of two fragments

表2 两颗粒形状参数值Table 2 Two fragments shape parameter values

2 CSR形态特征描述结果分析

2.1 CSR指标变化规律

分别选取具有相同矩形度(R)、圆形度(C)和球形度(S)的三组颗粒,对比分析其余两组参数随粒径(D)变化规律。相同R的颗粒组及另外两参数变化规律如图7和图8所示。

由图8可知,A、B和C三值主要集中在小粒径区且均为相同颗粒,圆形度随粒径降低,球形度变化幅度不明显。两参数取值最小、最大、均值的颗粒分别为粒径为13.33、17.83、18.75 mm的岩石颗粒,如图9所示。

图7 矩形度为0.75的岩石颗粒组Fig.7 Rock fragments group with rectangularity of 0.75

A1、B1、C1分别表示球形度最小值、最大值、均值;A2、B2、C2分别表示圆形度最小值、最大值、均值图8 具有相同R颗粒C、S随粒径变化Fig.8 Variation of C and S with fragments size for same R fragments

图9 C、S最小值、均值、最大值颗粒Fig.9 C, S minimum, mean, maximum fragments

三颗粒呈由狭长向近圆形变化,结合两参数变化特征认为C和S两者存在相关性,粒径对圆形度的影响程度更大。

相同圆形度颗粒组及另外两参数变化规律如图10和图11所示。

图10 圆形度为0.82的岩石颗粒组Fig.10 Rock fragments group with roundness of 0.82

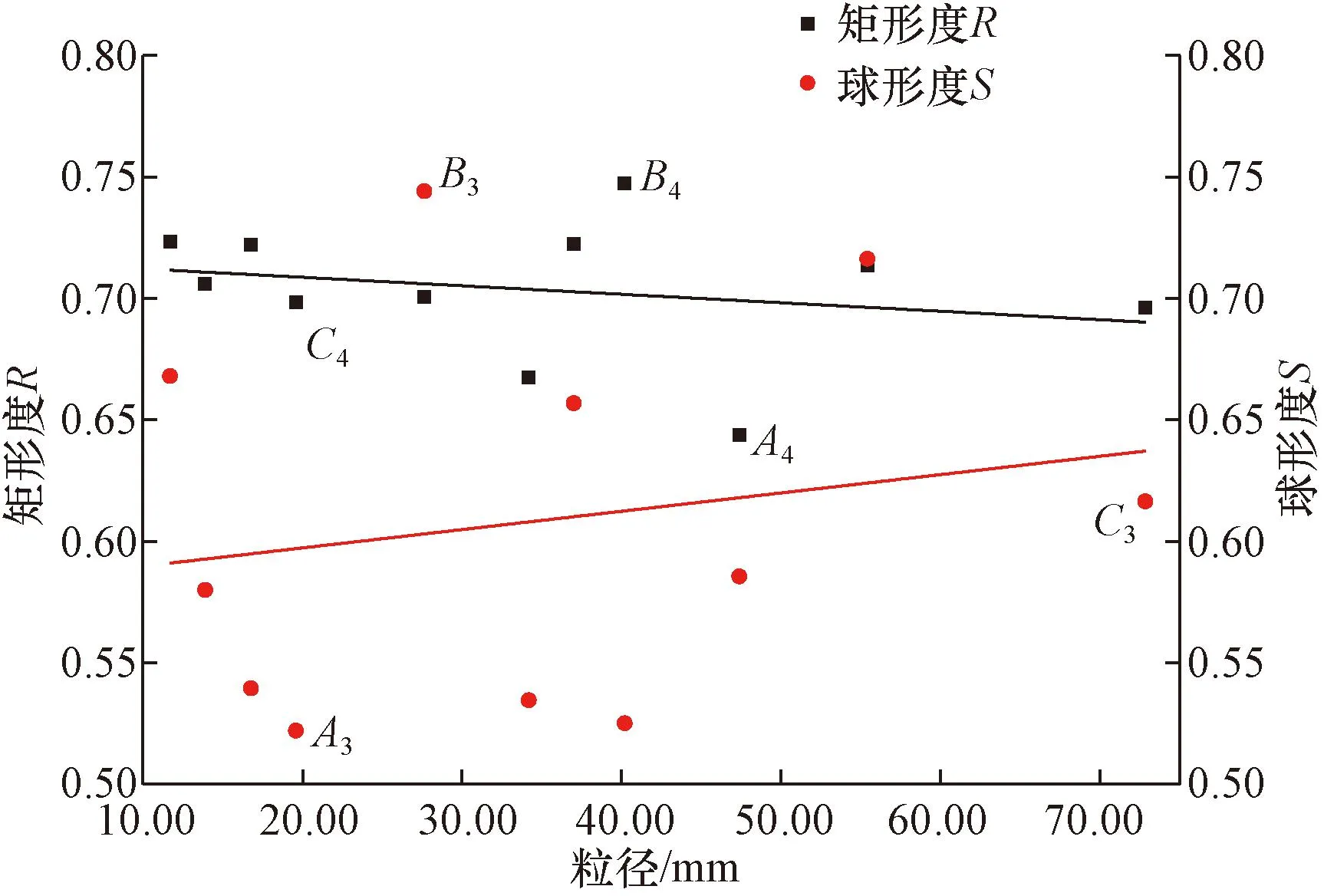
A3、B3、C3分别表示球形度最小值、最大值、均值;A4、B4、C4分别表示矩形度最小值、最大值、均值图11 具有相同C颗粒R、S随粒径变化Fig.11 Variation of R and S with fragments size of same C fragments

由图11可知,矩形度随粒径呈降低趋势,球形度则相反。最小值、最大值与均值均不为相同颗粒,三值随粒径分布比较分散。图像中两参数各指标无明显共同规律且球形度随粒径增幅更明显,判断两参数间无相关关系,粒径对球形度影响程度更大。

相同球形度颗粒组及另外两参数变化规律如图12、图13所示。

由拟合线可知,两参数均随粒径呈降低趋势,圆形度随粒径降幅更明显,最小值、最大值为相同颗粒,判定两参数存在相关关系,粒径对圆形度影响程度更大。

总结以上分析所得初步判定:

图12 球形度为0.57的岩石颗粒组Fig.12 Rock fragments group with sphericity of 0.57

A5、B5、C5分别表示矩形度最小值、最大值、均值;A6、B6、C6分别表示圆形度最小值、最大值、均值图13 具有相同S颗粒R、C随粒径变化Fig.13 Variation of R and C with fragments size of same S fragments

(1)C和S的相关性较强,D对C影响程度更大。

(2)R和S的相关性较弱,D对S影响程度更大。

(3)C、R的相关性较强,D对S的影响程度更大。

综合以上结果可知,由于破碎岩石颗粒形态特征的复杂性,当采用粒径作为唯一描述参数时难以保证其与形态特征的绝对相关性和影响程度的显著性。因此,需要进一步研究多因素控制下的参数指标相关关系,构建更为准确的描述体系。

2.2 CSR指标相关性分析

圆形度可以表征颗粒规则程度,以下将针对圆形度与其余形态指标的相关性开展分析。拟合C-S、C-R、C-D散点图,如图14所示。

图14 散点线性拟合图Fig.14 Linear fitting diagram of scattered points

由图14可知,C-R、C-D两图中散点的离散性较大,造成该现象的原因可归结为拟合的两参数相关性过低,需要结合拟合方程确定最终结果。拟合得到的回归方程分别为

C=0.462S+0.551

(14)

C=0.519R+0.441

(15)

C=-0.001D+0.852

(16)

三个回归方程均经F分布检验F>F0.05(1,98),认为在0.05置信区间上回归方程均显著,拟合有效,但决定系数R2分别为0.715 69、0.086 09、0.089 82,所以C-S的拟合效果更优,两参数相关性更大,在构建体系时,可采取式(14),另外两式相关性太低不予采纳,也印证了此前分析C-R、C-D散点图离散性大的原因。

体系中参与的形状参数越多则描述效果会越准确,因此进行三个参数的多元拟合,拟合得到的公式为

C=0.447S+0.194R+0.420

(17)

C=0.550R-0.001D+0.460

(18)

C=0.450 3S-0.000 3D+0.566 3

(19)

经F分布检验,认为三个方程式在0.05置信区间上显著,拟合有效。三个方程的决定系数R2分别为0.726、0.189、0.718,认为式(18)的拟合效果不理想,参数间相关性小,在构建体系时,式(18)不予采纳。

为量化分析单个参数的影响程度,检测另外两公式的偏回归系数,如表3所示。

表3 偏回归系数检测表Table 3 Partial regression coefficient detection table

由表3可知,式(17)的两偏回归系数均在0.05置信区间内效果显著,S的显著效果优于R。式(19)中S的偏回归系数影响效果显著,而D的偏回归系数影响效果不显著,一般原因一是D这一变量与C无相关性,二是D与S一起作为自变量时,S的影响效果极显著,D的解释力被S稀释,两者的影响程度差距悬殊,D的影响程度可忽略,但综合考虑C-D单独拟合时相关性极低的情况,认为是第一种原因,即粒径这一变量不适用于此颗粒描述体系。故式(17)可用于构建描述体系,式(18)与式(19)不予采纳。

为验证粒径不为影响因素,将C、S、R、D进行多元拟合,拟合公式为

C=0.431 3S+0.214 1R-0.000 3D+0.425 7

(20)

多元回归方程的决定系数R2为0.730,经F分布检验,在0.05置信区间上回归方程显著,拟合有效,三变量的偏回归系数显著效果如表4所示。

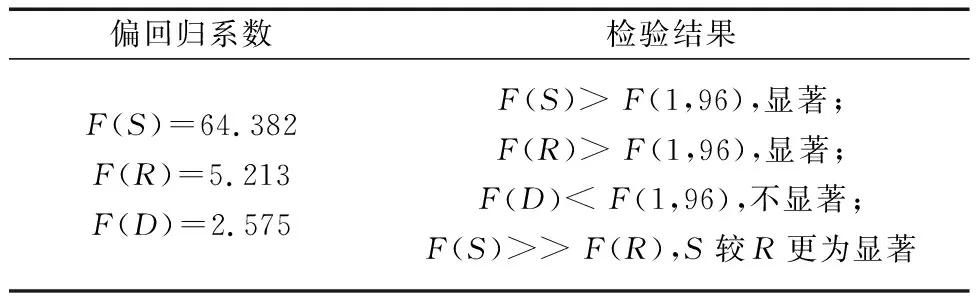
表4 S、R、D参量偏回归系数检验Table 4 S,R,D parameter partial regression coefficient test

由表4可知,式(20)中S与R的偏回归系数均在0.05置信区间内效果显著,且S的显著效果优R。D的偏回归系数影响效果并不显著,再一次验证了此前的判断,所以D不能作为变量,含D的公式不能作为描述系统的组成部分。

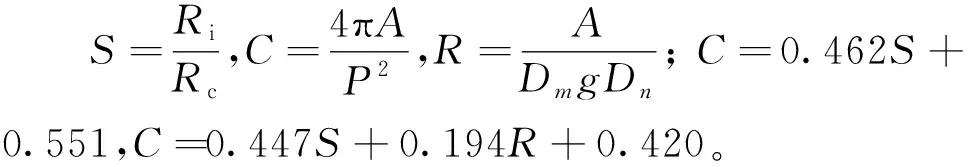
该体系可用于量化判断颗粒的规则程度,一定程度上为颗粒三维形态特征的量化描述提供一定思路,为后续研究奠定基础。

2.3 CSR指标相关性验证

为验证描述体系准确性,选取形态特征明显不同的典型岩石颗粒代表进行验证,如图15所示。

8个颗粒的图像处理测量值与描述体系计算值对比(结果均保留两位小数)如表5所示。

图15 不同形态特征代表颗粒Fig.15 Different morphological characteristics represent fragments

表5 测量值与计算值对比Table 5 Comparison of measured and calculated values

据表5中数据对比可知,除1、5两颗粒,其他颗粒的计算值与测量值均相近,式(17)的计算结果C2更贴近实际值,1、5两颗粒计算结果与实际值相差较大,原因可能为计算时取值精度不够产生了误差。综合而言,描述体系的准确度是可信的。

根据验证过程可知,在进行颗粒单独参数描述时,在测量后,由式(11)～式(13)得到任一测量值,由式(14)和式(17)得到计算值,将测量值与计算值对比,验证测量值准确性,方便对所使用的测量方法进行误差分析。

在建立描述体系初始,将C作为颗粒规则程度的量化标准,C值越大则颗粒规则性越高。最终确定的体系中包含两公式,根据验证结果来看,式(17)较式(14)获得的数值更接近测量值,说明体系中包含的参数越多则准确度越高。由于体系包含的三个形状参数均不含表征细观特征的基础数据,故此体系仅用于颗粒宏观形态特征描述,细观特征参数如粗糙度、棱角度等参数,后续可继续拓展,更新参数涵盖度,形成更加全面且完善的新体系。