时空分数阶扩散方程的高阶快速数值方法分析*

田洪材,曹俊英,王自强

(贵州民族大学 数据科学与信息工程学院,贵州 贵阳 550025)

1 背景

分数阶微积分应用范围广泛,可以描述一些具有记忆性、非局部性的自然现象。分数阶导数和分数阶微分方程被许多科学和工程领域的研究人员所研究[1]。其中,具有空间Riesz分数阶导数和时间Caputo分数阶导数的时空分数扩散方程涉及许多应用,如金融学[2]和分数动力学方程[3]。随着分数阶微分方程模型的增多和精确解的不易获得,人们对开发快速的数值方法产生了极大的兴趣。

Riesz分数阶导数被视为左右Riemann-Liouville分数阶导数的线性组合。本文研究时间为Caputo分数阶导数,空间为Riesz分数阶导数的时空分数阶扩散方程,对它的一个高阶快速的数值格式进行了构造和分析。

2 数值格式构造

考虑如下方程:

(1)

和初边值条件

u(x,0)=φ(x),x∈[a,b],

u(a,t)=u(b,t)=0,∀t∈[0,T],

0<α<1,1<β<2,

这里Γ(·)是伽马函数,f(x,t)和φ(x)为已知函数。

(2)

其中:

(3)

其中,kα=Γ(3-α)τα,pα=c1+2-0.5α。

当m=3时,

当m≥4时,

其中

(j+1)2-α-j2-α

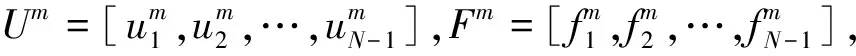
其中U0=[φ1,φ2,…,φN-1]。

利用文献[6]中的加权移位Grünwald-Letnikov差分方法在空间上和时间上利用式(2)与式(3),可得:

当m=1,2时,有:

(4)

当m≥3时,有:

(5)

其中,

D=

这里

wβ,0=λ1gβ,0,wβ,1=λ1gβ,1+λ2gβ,0,

wβ,k=λ1gβ,k+λ2gβ,k-1+λ3gβ,k-2,k≥2。

当m≥3时,数值格式(5)系数矩阵是一个Toeplitz矩阵,我们利用文献[7]和[8]的思想方法,结合GMRES迭代方法与FFT方法建立数值格式(5)的快速迭代方法(FGMRES)。

利用文献[9]中的思想方法,我们可以证明如下定理。

定理1:数值格式(5)的收敛阶为O(h2+τ3-α)。

3 数值实验

考虑一维时空分数阶扩散方程模型,我们有[a,b]=[0,1],T=1,该方程的精确解和右端项分别为:u(x,t)=t4x2(1-x)2,

f(x,t)=24x2(1-x)2(t4-α)/Γ(5-α)+

t4((3-β)(4-β)(x2-β+(1-x)2-β)-

6(4-β)(x3-β+(1-x)3-β)+12(x4-β+

(1-x)4-β))/(Γ(5-β)cos(βπ/2))

我们定义数值解与精确解的最大误差:

将空间步长相对时间步长取到很小,时间收敛阶为:

Order1=log2(E(2τ,h)/E(τ,h))

将时间步长相对空间步长取到很小,空间收敛阶为:

Order2=log2(E(τ,2h)/E(τ,h))

表1 误差与时间收敛阶(h=1/2000)

表2 误差与空间收敛阶(τ=1/800)

从表1、表2可看出,当α=0.5,β=1.75时,表1的时间收敛阶为2.5阶,表2的空间收敛阶是2阶。这样的结论符合定理1,因此从误差效果来看,我们所构造的高阶数值格式是有效的。

下面为了说明本文所用算法所需时间的有效性,我们用直接LU分解方法和本文所用算法FGMRES进行了比较。从表3可以看出,本文所用算法FGMRES的时间效率显然比直接LU分解方法的时间效率要好。

表3 FGMRES与LU方法所用时间(单位：s)

以上所有结果均在MATLAB R2016a在Intel(R)Core(TM)i5-4590 CPU @3.30GHz 3.30GHz和8.00GB内存的电脑中实现.